一种时滞电力系统特征值计算方法及系统与流程

本公开涉及一种时滞电力系统特征值计算方法及系统。

背景技术：

本部分的陈述仅仅是提供了与本公开相关的背景技术信息，不必然构成在先技术。

随着电网互联规模的增大，长距离大容量电力输送工程不断增加，电力系统中固有的小干扰稳定问题成为影响互联电网功率输送稳定性的重要因素之一。区域间的低频振荡成为限制区域联络线输送功率大小，甚至影响互联电网安全稳定运行的主要因素之一。输入为本地信号的pss能够有效地提高区域内低频振荡(频率大于1hz)的阻尼；而本地信号对于区域间的低频振荡(频率为0.25～1hz)的可控、可观性较差，甚至不可控、不可观，区域间的低频振荡往往缺乏足够的阻尼。基于同步相量单元(phasormeasurementunit，pmu)的广域量测系统(wide-areameasurementsystem，wams)能够同步采集电力系统的运行数据，实时获取电力系统的状态感知，给大规模互联电力系统稳定分析与控制的发展带来新的契机。

随着信息和通信技术的发展，传统电力系统已经转变成一个具有实时感知、动态控制和信息服务等功能的信息物理融合电力系统(cyber-physicalpowersystem,cpps)。基于wams的广域阻尼控制器(wide-areadampingcontroller，wadc)可以有效提高区间低频振荡的阻尼水平，是广域量测技术最先得到应用的领域之一。然而，广域测量信号在采集、路由、传输和处理过程中存在数十到几百毫秒的时延，电力系统因此成为时滞信息物理融合的电力系统(delayedcpps,dcpps)。广域阻尼控制回路中的通信时滞会使系统稳定性恶化，严重时导致其失稳，因此有必要分析大规模时滞电力系统的小干扰稳定性。

在现代电力系统分析中，大规模时滞电力系统小干扰稳定性分析方法总体上可以分为时域法和频域法两类。时域法存在其固有的保守型；在频域法中，时滞作为指数项出现，最有效的分析方法是基于谱离散化的特征值分析方法。然而，基于谱离散化的时滞电力系统的特征分析方法，虽然可以精确计算出大规模时滞电力系统实部较大或阻尼较小的部分特征值，但在离散化过程中生成的近似矩阵维数较大，存在计算量大的缺点。

特别是在分析大规模电力系统时，由于较大的矩阵维数问题，不可避免的产生较大的计算量与计算时间，在一定程度上限制了算法的计算效率。

技术实现要素：

本公开为了解决上述问题，提出了一种时滞电力系统特征值计算方法及系统，本公开基于低阶解算子伪谱配置离散化(low-orderpseudo-spectraldiscretizationofsolutionoperator,lo-sod-ps)方法,能够高效计算时滞电力系统的关键特征值,即机电振荡模式。

根据一些实施例，本公开采用如下技术方案：

一种时滞电力系统特征值计算方法,包括以下步骤:

建立时滞电力系统的动态模型，将其线性化得到线性化后的系统状态方程，并得到相应的特征方程；

根据与时滞是否相关将时滞电力系统的状态变量划分为与时滞无关项和与时滞有关项，将系统的状态方程转化为常微分方程和时滞微分方程的组合；

利用解算子将时滞电力系统的状态方程转换为抽象柯西问题，将时滞电力系统的特征值计算问题转换为解算子的特征值求解问题；

对解算子进行离散化，通过各个离散点处的状态方程得到解算子的低阶离散化矩阵；

对解算子的低阶离散化矩阵进行旋转-放大变换，将时滞电力系统的机电振荡模式转换为模值较大的特征值，将得到的特征值经过旋转-放大反变换，利用牛顿法校验进行修正，得到时滞电力系统的精确特征值。

作为进一步的限定，时滞电力系统模型为：

式中，f和g分别为微分方程和代数方程；和分别为t时刻系统的状态变量和代数变量；n为系统状态变量总数；l为系统代数变量总数；t为当前时刻；xdi和ydi(i＝1,2,…,m)分别为时滞状态变量和代数变量；

xdi＝x(t-τi),ydi＝y(t-τi),i＝1,2,…,m

式中，τi>0(i＝1,2,…,m)为m个时滞常数，且满足0＝τ0<τ1<…<τm＝τmax，τmax为最大的时滞。

作为进一步的限定，对时滞电力系统模型进行平衡点处的线性化，消去代数变量，得到时滞微分方程为：

式中，δx(0)为系统状态变量的初始，简写为和分别为稠密的系统状态矩阵和稀疏的时滞状态矩阵。

作为进一步的限定，将时滞微分方程转换为常微分方程(ode)和时滞微分方程(dde)的组合的具体过程包括：

设n1和n2分别为与时滞相关和与时滞无关的系统状态变量个数，n1+n2＝n，将状态变量δx分为与时滞无关项和与时滞相关项即将时滞微分方程(4)转换转化为n1阶的ode和n2阶的dde的组合，即

式中，和为系统状态矩阵的分块子矩阵，均为稠密矩阵；为系统时滞状态矩阵的分块子矩阵，为稀疏矩阵。

作为进一步的限定，将时滞电力系统的状态方程转换为抽象柯西问题，进而将时滞电力系统的特征值计算问题转换为解算子的特征值求解问题的具体过程包括：

定义时滞系统在θ+t时刻的状态，根据皮卡-林德勒夫定理给出θ>0时的时滞系统的全局唯一解，得到以泛函为状态变量的解算子分段函数表示的解算子显式表达，以用来表征时滞系统初始状态和不同时刻的状态之间的关系。

作为进一步的限定，对解算子进行离散化，通过各个离散点处的状态方程得到解算子的低阶离散化矩阵的具体过程包括：

采用伪谱离散化方案对解算子进行离散化，通过时滞区间上的多个离散点将时滞区间划分为离散函数空间，将连续函数离散化为分块向量；

在对过去时刻的时滞电力系统状态进行离散化时，剔除与时滞无关的状态变量的离散化，只保留对与时滞相关的状态进行的离散化，由得到的离散点处的状态方程得到解算子的低阶离散化矩阵，将无限维的特征值问题转化为有限维的特征值问题。

作为进一步的限定，对解算子的低阶离散化矩阵进行旋转-放大变换。

作为进一步的限定，采用部分特征值算法计算解算子伪谱配置离散化矩阵模值最大的部分特征值，即对应时滞电力系统的机电振荡模式。

作为进一步的限定，通过对应时滞电力系统的机电振荡模式与解算子特征值之间的映射关系式，最终得到时滞信息物理融合的电力系统特征值的估计值，利用牛顿法对估计值校验进行修正，得到时滞电力系统的精确特征值。

一种时滞电力系统特征值计算系统，运行于处理器或存储器上，被配置为执行以下指令：

建立时滞电力系统的动态模型，将其线性化得到线性化后的系统状态方程，并得到相应的特征方程；

根据与时滞是否相关将时滞电力系统的状态变量划分为与时滞无关项和与时滞有关项，将系统的状态方程转化为常微分方程和时滞微分方程的组合；

利用解算子将时滞电力系统的状态方程转换为抽象柯西问题，将时滞电力系统的特征值计算问题转换为解算子的特征值求解问题；

对解算子进行离散化，通过各个离散点处的状态方程得到解算子的低阶离散化矩阵；

对解算子的低阶离散化矩阵进行旋转-放大变换，将时滞电力系统的机电振荡模式转换为模值较大的特征值，将得到的特征值经过旋转-放大反变换，利用牛顿法校验进行修正，得到时滞电力系统的精确特征值。

与现有技术相比，本公开的有益效果为：

本公开提出的基于低阶解算子伪谱离散化算法的时滞电力系统特征值分析方法可以适用于计算dcpps的机电振荡模式，从根本上解决了较大地离散化矩阵维数对计算效率的限制，使算法能够高效地计算dcpps的机电振荡模式。

本公开通过删除与时滞无关状态变量的离散化，只保留与时滞相关的状态变量的离散化，最终大大减少了解算子离散化矩阵的维数。从而在保证精算精度的同时，大大降低了dcpps机电振荡模式计算的计算量。

本公开充分利用系统增广矩阵和解算子伪谱离散化矩阵的稀疏性，减少本公开的特征值计算方法中矩阵-向量乘积的计算量。

本公开能够应用于大规模时滞电力系统的关键特征值的高效、准确计算，这对于完善和丰富基于特征值的小干扰稳定性分析理论，具有重要的意义和价值。

附图说明

构成本申请的一部分的说明书附图用来提供对本申请的进一步理解，本申请的示意性实施例及其说明用于解释本申请，并不构成对本申请的不当限定。

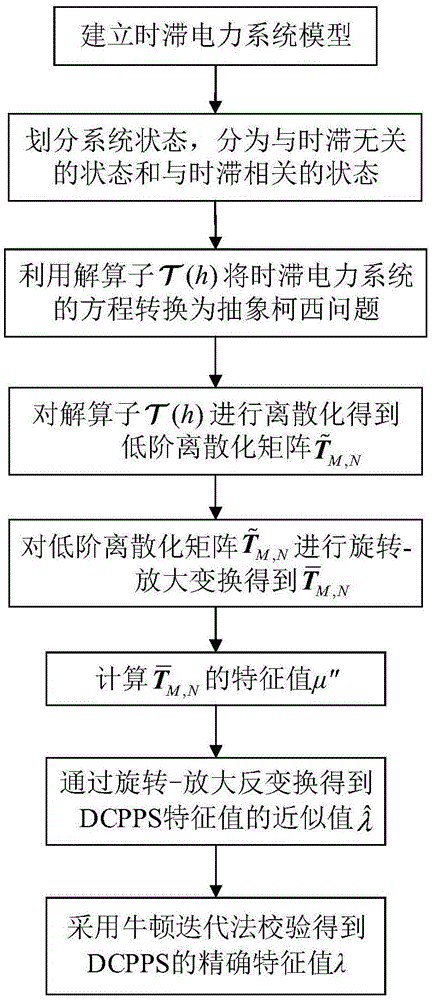
图1为基于lo-sod-ps算法的时滞电力系统特征值计算方法流程图。

图2为离散点集合ωm；

具体实施方式：

下面结合附图与实施例对本公开作进一步说明。

应该指出，以下详细说明都是例示性的，旨在对本申请提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

在本公开中，术语如“上”、“下”、“左”、“右”、“前”、“后”、“竖直”、“水平”、“侧”、“底”等指示的方位或位置关系为基于附图所示的方位或位置关系，只是为了便于叙述本公开各部件或元件结构关系而确定的关系词，并非特指本公开中任一部件或元件，不能理解为对本公开的限制。

本公开中，术语如“固接”、“相连”、“连接”等应做广义理解，表示可以是固定连接，也可以是一体地连接或可拆卸连接；可以是直接相连，也可以通过中间媒介间接相连。对于本领域的相关科研或技术人员，可以根据具体情况确定上述术语在本公开中的具体含义，不能理解为对本公开的限制。

如图1所示：基于lo-sod-ps(低阶解算子伪谱配置离散化(low-orderpseudo-spectraldiscretizationofsolutionoperator,lo-sod-ps))的时滞电力系统特征值计算方法，包括如下步骤：

步骤(1)：建立dcpps动态模型并对其进行线性化，从而得到系统的状态方程，并依此给出dcpps的特征方程。

步骤(2)：划分系统状态，分为与时滞无关的状态和与时滞相关的状态。从而将系统的状态方程转化为常微分方程(ordinarydifferentialequation,ode)和时滞微分方程(delayeddifferentialequation,dde)的组合。

步骤(3)：利用解算子将时滞电力系统的状态方程转换为抽象柯西问题，进而将时滞电力系统的特征值计算问题转换为解算子的特征值求解问题。

步骤(4)：采用伪谱离散化方案对解算子进行离散化，通过时滞区间上的多个离散点将时滞区间划分为离散函数空间，从而将连续函数离散化为分块向量；然后，在在对过去时刻的时滞电力系统状态进行离散化时，剔除与时滞无关的状态变量的离散化，只保留对与时滞相关的状态进行的离散化，从而由这些离散点处的状态方程得到解算子的低阶离散化矩阵从而将无限维的特征值问题转化为有限维的特征值问题。

步骤(5)：对解算子的低阶离散化矩阵进行旋转-放大变换预处理，从而得到预处理后的低阶离散化矩阵

步骤(6)：采用部分特征值算法计算低阶离散化矩阵模值最大的部分特征值μ″，即对应时滞电力系统的机电振荡模式。

步骤(7)：将得到的特征值μ″经过旋转-放大反变换，从而得到时滞电力系统关键特征值的近似值

步骤(8)：利用牛顿法校验对进行修正即可得到时滞电力系统的精确特征值λ。

所述步骤(1)中，时滞电力系统模型可以表示如下：

式中，f和g分别为微分方程和代数方程；和分别为t时刻系统的状态变量和代数变量；n为系统状态变量总数；l为系统代数变量总数；t为当前时刻；xdi和ydi(i＝1,2,…,m)分别为时滞状态变量和代数变量。

xdi＝x(t-τi),ydi＝y(t-τi),i＝1,2,…,m(2)

式中，τi>0(i＝1,2,…,m)为m个时滞常数，且满足0＝τ0<τ1<…<τm＝τmax，τmax为最大的时滞。

将式(1)在平衡点处进行线性化，可得

式中，表示系统t时刻状态变量导数的增量；δx和δy分别表示增量形式的t时刻系统状态变量和代数变量向量；δxdi和δydi分别表示增量形式的t-τi时刻系统状态变量和代数变量向量；(i＝1,2,…,m)为高度稀疏的雅可比矩阵，也被称为系统的增广状态矩阵。其中，ci＝c0，di＝d0，i＝1,2,…,m。

由于状态矩阵d0非奇异，可将式(3)中的代数变量δy和δydi(i＝1,2,…,m)消去。从而，可得如下dde：

式中，δx(0)为系统状态变量的初始，简写为和分别为稠密的系统状态矩阵和稀疏的时滞状态矩阵。在后续分析中，和只具有理论分析的意义，为充分利用其稀疏性，计算时采用其增广形式，即：

与式(4)对应的特征方程为：

式中，λ和分别为特征值及其对应的右特征向量。

式(7)的等价增广形式为：

式中，为中间和辅助向量，a'(λ)和b'(λ)可具体表示为：

步骤(2)中，将式(4)转化为ode和dde的组合。

设n1和n2分别为与时滞相关和与时滞无关的系统状态变量个数，n1+n2＝n。如图1所示，可将状态变量δx分为与时滞无关项和与时滞相关项即于是，式(4)可转化为n1阶的ode和n2阶的dde的组合，即

式中，和为系统状态矩阵的分块子矩阵，均为稠密矩阵；为系统时滞状态矩阵的分块子矩阵，为稀疏矩阵。这些矩阵均可由ai,bi和ci(i＝0,1,…,m)的稀疏分块计算得到。

其中，和为ai的分块矩阵；为bi的分块矩阵；为ci的分块矩阵。这些分块矩阵均是高度稀疏的。

此外，为方便后续使用，给出如下定义和故，式(11)可以写作

步骤(3)中，基于解算子的定义，将时滞电力系统的状态方程转换为抽象柯西问题，进而将时滞电力系统的特征值计算问题转换为解算子的特征值求解问题；

将时滞系统在θ+t时刻的状态δx(θ+t)定义为δxt(θ)∈x：

当θ>0时，时滞系统的全局唯一解δx(θ)由定理给出：

由此，可以得到以泛函δxs为状态变量的的分段函数表示的解算子显式表达，即式(17)。

式中，解算子x→x用来表征时滞系统初始状态和不同时刻的状态之间的关系。

由谱映射定理可知，时滞电力系统的特征值λ与解算子的非零特征值μ之间存在如下关系：

式中，\表示集合差运算。其对应的特征方程为：

步骤(4)中，由于解算子的特征值有无穷多个，需要对解算子进行离散化。

设状态空间是由区间[-τmax,0]到n维实数空间映射的连续函数构成的巴拿赫(banach)空间，并赋有上确界范数首先，将区间[-τmax,0]分成q个子区间[θ1,θ0],[θ2,θ1],…,[θq,θq-1]。其中，q为大于或等于τmax/h的最小整数，即且θ＝-τmax。然后，利用m阶第二类chebyshev多项式的m+1个经过位移和归一化处理后的零点对q个子区间分别进行离散化。最后，得到区间[-τmax,0]上qm+1个离散点构成的集合ωm，如图2所示。

利用集合ωm，可将空间x离散化为离散函数空间在集合ωm的各离散点上，任意连续函数被离散化为分块向量其中离散函数是连续函数在离散点θm,i,j处函数值的近似，此外，有φi,m＝φi+1,0,i＝1,2,…,q-1。

定义为由区间[0,h]到n维实数空间映射的连续函数构成的巴拿赫空间，并赋有上确界范数||z||＝sup[0,h]|z(θ)|。选择n阶第一类chebyshev多项式的n个零点，经过位移和归一化处理后，对区间[0,h]进行离散化，从而得到具有n个元素的集合利用集合可将空间x⁺离散化为在集合的各离散点上，任意连续函数z∈x⁺被离散化为分块向量其中离散函数是连续函数z在离散点tn,i处函数值的近似，

在以上各离散点处只保留对与时滞相关的状态的离散化，由这些离散点处的状态方程得到解算子的低阶离散化矩阵

式中各矩阵形式分别表示如下：

(1)矩阵的形式为

式中，和分别是维数为n1和n2的单位矩阵；是维数为n2的零矩阵；tq,k,l(k＝0,1,…,m；l＝0,1,…,m)是通过对拉格朗日插值系数进行运算得到；1^m×1是m维的列向量；i^(q-2)m是维数为(q-2)m的单位矩阵；0^(m+1)×m是维数为(m+1)行、m列的零矩阵；表示克罗内克积；矩阵和分别为

(2)矩阵的形式为

式中，和分别为n1行、n2列和n2行、n1列的零矩阵；0((q-1)m+1)×n是(q-1)m行、n列的零矩阵；ek,j(k＝1,2,…,m；j＝1,2,…,n)是通过对拉格朗日插值系数进行运算得到；矩阵为

(3)矩阵的形式为

式中，其元素通过对拉格朗日插值系数进行运算得到。

(4)矩阵的形式为

式中，其元素通过对拉格朗日插值系数进行运算得到。

到目前为止，时滞电力系统的特征值计算问题已转化为求解解算子的低阶离散化矩阵的特征值。

所述步骤(5)中，对进行旋转-放大变换，h被变换原来的α(α为放大倍数)倍，变为

式中，θ为旋转角度。

通过如下步骤得到解算子的伪谱配置离散化矩阵。首先，将区间[-τmax,0]重新划分为长度等于(或小于)αh的q'个子区间，从而得到新的离散化空间xm。其次，将空间x⁺重新定义为然后，利用区间[0,αh]的n个离散点将x⁺离散化为进而将矩阵u′m,um,σn,分别更新为最后，形成的解算子伪谱配置离散化矩阵可表示为

式中，和分别通过更新式(21)、式(24)、式(26)和式(27)得到：

式(30)-式(33)中，和分别是通过对拉格朗日插值系数进行更新运算得到。和定义如下：

步骤(6)中，采用部分特征值算法计算模值最大的部分特征值，即对应时滞电力系统的机电振荡模式μ"。

步骤(7)中，通过的特征值μ"与电力系统特征值λ之间的映射关系式，最终得到dcpps特征值的估计值

步骤(8)中，利用牛顿法对校验进行修正即可得到时滞电力系统的精确特征值λ。

以上所述仅为本申请的优选实施例而已，并不用于限制本申请，对于本领域的技术人员来说，本申请可以有各种更改和变化。凡在本申请的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本申请的保护范围之内。

上述虽然结合附图对本公开的具体实施方式进行了描述，但并非对本公开保护范围的限制，所属领域技术人员应该明白，在本公开的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本公开的保护范围以内。