一种再生核粒子算法实现结构线性静力学仿真方法与流程

本发明涉及计算机辅助工程中的仿真计算领域，尤其涉及一种再生核粒子算法实现结构线性静力学仿真方法。

背景技术：

结构静力学仿真是利用计算机程序对工程中的实际结构进行力学性能计算的过程，利用求解得到的结果可以对结构进行强度校核和刚度校核。当在其实际工况作用下，结构的位移与载荷的关系成线性变化时，则被认为是线性问题。目前，用于结构线性静力学仿真的计算机程序都是基于有限元法。有限元法在早期是以变分原理为基础发展起来的，所以广泛地应用于以拉普拉斯方程和泊松方程所描述的各类物理场中。其基本思想是：将无限自由度的结构近似离散成有限个自由度，通过构建自由度之间的关系函数，求解泛函的极值。

尽管有限元法在结构线性静力学仿真中的应用极其广泛，而且也非常成熟，但是由其自身算法带来的局限性，技术人员一直也在需求突破。一方面，有限元法的前提是利用单元对结构进行离散，即在程序求解前，需要生成单元，对于复杂的几何模型，这个过程需要花费工程师大量的时间和精力，很大程度上限制了工程师对结构设计方案进行快速验证迭代；另一方面，有限元法对网格尺寸和质量特别敏感和依赖，结构线性静力学仿真的结果精度很大程度依赖于结构网格处理的好坏，而求解效率又会随着网格尺寸的细化而大幅降低。

近年来，再生核粒子算法作为先进的无网格算法被引入到结构线性静力学仿真计算中，其具有基于网格的有限元法所不具备的优点。其在模型前处理时，无需如同有限元法那样划分网格，因此可以对任意复杂的几何模型进行快速前处理，可以大大节省复杂几何模型进行前处理的时间。没有网格尺寸和质量的牵制，结构线性静力学仿真的求解精度和效率也到了最大程度的保障。基于这么多的核心优势，目前再生核粒子算法成为了最前沿的研究方向，受到技术人员的广泛关注。

技术实现要素：

本发明的目的是提供一种再生核粒子算法实现结构线性静力学仿真方法，可以克服传统方法中对网格的依赖，简化了复杂模型的前处理过程，提升了结构线性静力学仿真的求解精度和求解效率。

为实现上述目的，本发明采用以下技术方案：

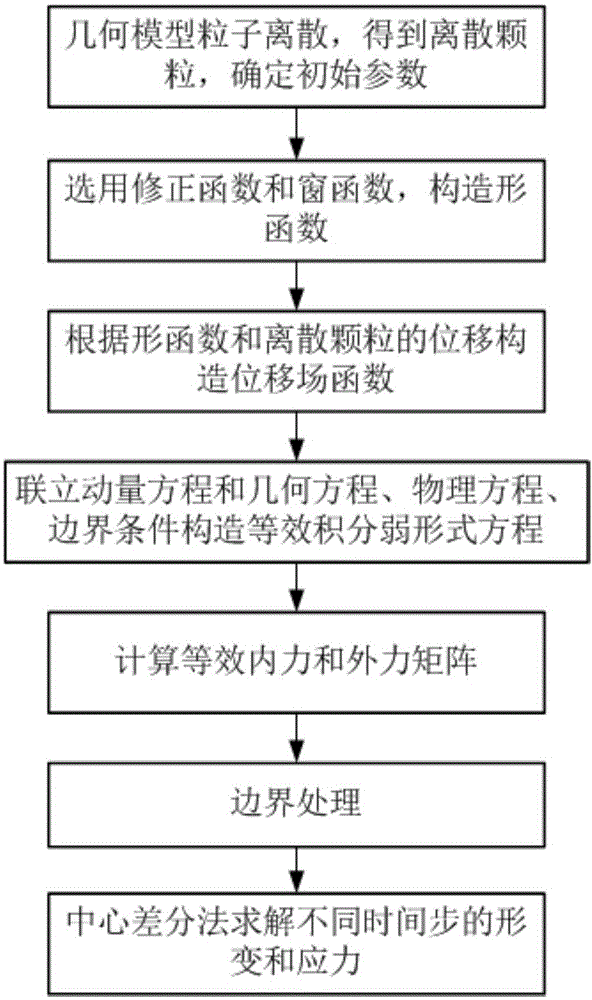
一种再生核粒子算法实现结构线性静力学仿真方法，包括如下步骤：

(1)按照给定的粒子密度对仿真几何模型进行粒子离散，得到离散颗粒，确定所述离散颗粒的初始位置、影响域ω和影响域半径ρ；

(2)基于再生核粒子算法，选用修正函数和窗函数的类型，构造所述影响域内所述离散颗粒的形函数；

(3)根据所述离散颗粒的位置和所述影响域半径ρ，利用所述影响域ω内的所述离散颗粒的位移和所述形函数构造位移场函数；

(4)利用边界转化方法进行边界处理，消除边界不一致性引起的误差；

(5)联立动量方程和几何方程、物理方程、边界条件构造等效积分弱形式方程；

(6)构造位移矩阵，将所述位移场函数带入所述等效积分弱形式方程求解，得到等效内力和外力矩阵；

(7)利用中心差分法对等效积分弱形式方程进行代数求解，得到不同时间步的形变和应力。

优选地，步骤(1)中，所述离散颗粒的几何形状包括、但不限于圆形、球形、矩形、立方体。

优选地，步骤(1)中，所述影响域ω由每个所述离散颗粒指定。

优选地，步骤(1)中，所述影响域半径ρ对于所有所述离散颗粒为恒定值或者对于每个单独的所述离散颗粒为不同的。

优选地，步骤(2)中，基于再生核粒子算法，所述形函数φρ(x,x-y)为：

φρ(x；x-y)＝cρ(x；x-y)kρ(x-y)

式中，cρ(x,x-y)为满足再生条件的修正函数，kρ(x-y)为满足再生条件的窗函数；

所述修正函数cρ(x,x-y)是由多项式基函数的线性组合表示而成，如下：

cρ(x；x-y)＝c0(x)+c1(x)(x-y)+c2(x)(x-y)²+…+cn(x)(x-y)ⁿ＝h^t(x-y)c(x)

其中，n是满足再生条件的次数，h^t(x-y)是n次多项式基函数的向量；c(x)为系数向量，通过施加n次再生条件来确定；ci(x)为系数(i＝1,2,3……n)；

h^t(x-y)＝[1,x-y,(x-y)²,…,(x-y)ⁿ]

c(x)＝[c0(x),c1(x),…,cn(x)]

所述窗函数κρ(x-y)是二维窗函数：

其中，为中间变量。

更优选地，所述窗函数选用三次样条函数，如下：

式中，

更优选地，所述窗函数包括、但不限于三次样条函数、b样条函数、高斯函数。

优选地，步骤(3)中，所述位移场函数u^r(x)为：

式中，u(y)表示所述影响域ω内的所述离散颗粒的位移；

将影响域ω用np个所述离散粒子离散，获得所述全场位移场函数的离散近似式：

式中，np表示所述影响域ω内的所述离散粒子的总点数，ui对应所述离散粒子i处的位移,δvi为离散粒子的体积权重，ni(x)为所述离散粒子i处的形函数，i＝1，2，……np。

优选地，所述步骤(4)中，所述边界转化方法将所述位移场函数u^r(x)分为两部分

式中，b表示位移边界上的离散颗粒，nb表示除去位移边界上的离散颗粒剩下的所有离散颗粒；位移边界上的离散颗粒总数为nb，nnb＝np-nb。n^b(x)为边界插值点上的形函数，n^nb(x)为非边界插值点的形函数，u^b为边界插值点位移，u^nb为非边界插值点位移；

通过强制位移边界条件消除误差，假定

u^b＝(d^b)^-1g

式中：g表示边界位移，d^b通过下式构造

优选地，所述步骤(5)中，

动量方程：

几何方程：εij＝luij(2)

物理方程：σij＝dεij(3)

边界条件：

式中：σij表示应力分量，εij表示应变分量，ρ为密度，bi为体积力，l为计算微分算子，d为弹性矩阵，nj表示边界法向量，ti为边界载荷力，为边界位移；uij为位移，sσ为载荷边界域，su为位移边界域，νi为边界位移；

把式(2)、式(3)、式(4)带入式(1)，联立上述方程得到动量方程的等效积分弱形式方程：

上式中，δui,j为i方向位移对xj坐标求偏导，v为求解体积域，s为边界域，a为面积域，uij为ij方向的位移，ui为i方向位移，为i方向的加速度，为sσ边界域上的外力。

优选地，所述步骤(6)中，将重构的位移场函数u^r(x)带入等效积分弱形式方程，并将该方程写成矩阵形式得到下式：

mü+f^int＝f^evt

式中，m为质量矩阵，为加速度场，f^int为等效内力矩阵，f^ext为等效外力矩阵。

优选地，所述步骤(7)中，所述中心差分法将时间平均分为n个时间间隔，0，δt，…t时刻的位移、速度、加速度已知，求解t+δt时刻对应的解；

t时刻的加速度和速度利用中心差分法表示为

式中，ut-δt(x)为离散颗粒在t-δt时刻的位移，ut(x)为离散颗粒在t时刻的位移，ut+δt(x)为离散颗粒在t+δt时刻的位移；

t+δt时刻的位移解答可以根据时间t时刻的运动方程得到，即为下式

式中，m、c和k分别代表影响域的质量矩阵、阻尼矩阵和刚度矩阵；ft是t时刻外力和；

由此可得到中心差分法的递推公式

若t与t-δt时刻的位移已知，则可以进一步求解出t+δt时刻的位移。

利用步骤(5)中的几何方程，将不同时刻位移带入计算，得到形变，即应变，再利用步骤(5)中的物理方程求解，将应变带入计算得到应力。

本发明提供了一种实现结构线性静力仿真的全新的求解方法，与现有技术相比，有益效果在于：

1.简化了复杂模型的前处理过程。现在广泛应用的有限元法，需要在前处理时对结构进行离散化，将几何模型划分成有限个相互连接、互不重合的单元，对于复杂的几何模型，边界几何复杂，需要表征的小特征特别多，这些都使得划分网格的过程耗时耗力；而再生核粒子算法本质上是无网格法，无需划分网格，使用粒子对结构进行离散，只需给定粒子的密度，大大简化了前处理的过程。

2.提升了结构线性静力学仿真的求解精度和求解效率。现广泛应用的有限元法，在每一单元上通过多项式插值构造未知场函数的近似解，因此程序求解的精度和效率会很大程度上依赖于网格的尺寸和质量；而再生核粒子算法，是一种无网格法，回避了网格尺寸和质量对求解精度的影响，另外，再生核粒子算法依据离散颗粒的初始位置，结合选用的修正函数和窗函数，构造形函数，进而根据支持域的半径，生成位移场函数，其构造的形函数和常函数，相比较于有限元法，阶次更高，因此求解精度也更高。

附图说明

构成本申请的一部分附图用来提供对本申请的进一步理解，本申请的示意性实施例及其说明用于解释本申请，并不构成对本申请的不当限定。在附图中：

图1是本发明的一种再生核粒子实现结构线性静力仿真方法的流程图。

图2是本发明的一种再生核粒子实现结构线性静力仿真方法的示意性的离散颗粒的影响域二维示图。

图3是本发明中再生核粒子算法与有限元法实现结构线性静力学仿真的求解精度比较图。

具体实施方式

本发明提供一种再生核粒子实现结构线性静力仿真方法，为使本发明的目的、技术方案及效果更加清楚、明确，以下参照附图并举实例对本发明进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

图1是本发明一种再生核粒子实现结构线性静力仿真方法的流程图。

结合图1，本发明所述的一种再生核粒子实现结构线性静力仿真方法，包括如下步骤：

步骤1：按照给定的粒子密度对仿真几何模型进行粒子离散，得到离散颗粒，确定所述离散颗粒的初始位置、影响域ω和影响域半径ρ。

其中，所述离散颗粒可以为圆形或球形，也可以为其他不同的几何形状，例如，矩形、立方体等。粒子离散后的所述几何模型由多个所述离散颗粒代表。影响域是指一个离散颗粒的影响区域，所述影响域由每个离散颗粒指定，这通过为每个离散颗粒指定影响域半径而完成。

图2是本发明本发明的一种再生核粒子实现结构线性静力仿真方法的示意性的离散颗粒的影响域二维示图。如图2所示，示意性离散颗粒100(黑色实心圆)指定影响域101(虚线圆区域)。设置在所述影响域101内的离散颗粒为实线圆103，而设置在影响域101外的离散颗粒为虚线圆102。每个离散颗粒具有它自身的影响域。所述影响域半径ρ104用来控制所述离散颗粒的影响域的尺寸，对于所有离散颗粒为恒定值或者对于每个单独的所述离散颗粒为不同的。

步骤2：基于再生核粒子算法，选用修正函数和窗函数的类型，构造所述影响域内所述离散颗粒的形函数。

基于再生核粒子算法，所述形函数φρ(x,x-y)为：

φρ(x；x-y)＝cρ(x；x-y)kρ(x-y)

式中，cρ(x,x-y)为满足再生条件的修正函数或改进函数，它决定近似的完备性与一致性；kρ(x-y)为满足再生条件的窗函数，它是用来表征影响域内离散颗粒的光滑性和紧支性的函数，用于控制计算的连续性。

所述修正函数cρ(x,x-y)是由多项式基函数的线性组合表示而成，如下：

cρ(x；x-y)＝c0(x)+c1(x)(x-y)+c2(x)(x-y)²+…+cn(x)(x-y)ⁿ＝h^t(x-y)c(x)

其中，n是满足再生条件的次数，h^t(x-y)是n次多项式基函数的向量；c(x)为系数向量，通过施加n次再生条件来确定；ci(x)为系数(i＝1,2,3……n)；

h^t(x-y)＝[1,x-y,(x-y)²,…,(x-y)ⁿ]

c(x)＝[c0(x),c1(x),…,cn(x)]

所述窗函数κρ(x-y)是二维窗函数：

其中，为中间变量。

所述窗函数可以是、但不限于三次样条函数、b样条函数、高斯函数。

由于样条型核函数具有紧支撑特性，因此在大多数数值计算中经常采用该类型的核函数以节省计算时间。本实例中，所述窗函数选用三次样条函数，具体如下：

式中，

步骤3：根据所述影响域内的所述离散颗粒的位移和所述形函数构造位移场函数。

再生核粒子算法通过构造形函数建立位移场函数和离散颗粒处函数的关系，从而得到位移场函数，进一步进行求解。

所述位移场函数u^r(x)具体构造如下所示：

式中，u(y)表示所述影响域内的所述离散颗粒的位移；

将影响域ω用np个所述离散粒子离散，获得所述全场位移场函数的离散近似式：

式中，np表示所述影响域ω内的所述离散粒子的总点数，ui对应所述离散粒子i处的位移,δvi为离散粒子的体积权重，ni(x)为所述离散粒子i处的形函数，i＝1，2，……np。

步骤4：利用边界转化方法进行边界处理，消除边界不一致性引起的误差。

无网格法均不能自然满足位移边界条件，因此在计算过程中必须采用适当的方法来强制满足边界条件，常用的方法有：拉格朗日乘子法、再生核粒子插值技术、修正变分原理法、坐标变换法等。这些方法大多数致力于构建具有kroneckerdalta特性的近似函数，各有其特点，适用于不同场合。例如拉格朗日乘子法其系数矩阵即不正定又不呈带状，所以运算量很大，但这一方法的精确度很高，适用于求解小规模二维问题；修正变原理法的系数矩阵虽然保持正定和带状性，但精度不高。但总的说来，和其他无网络方法一样，还没有一种简单而又完美的方法来处理再生核粒子的边界条件。因此，边界条件的处理是目前无网格方法研究的热点之一，直接关系到无网格方法的实用性。

本实施例中，采用一种对再生核粒子方法适用的一致方法。所述一致方法将所述位移场函数u^r(x)分为两部分

式中，b表示位移边界上的离散颗粒，nb表示除去位移边界上的离散颗粒剩下的所有离散颗粒；位移边界上的离散颗粒总数为nb，nnb＝np-nb。n^b(x)为边界插值点上的形函数，n^nb(x)为非边界插值点的形函数，u^b为边界插值点位移，u^nb为非边界插值点位移；

通过强制位移边界条件消除误差，假定

u^b＝(d^b)^-1g

式中：g表示边界位移，d^b通过下式构造

步骤5：联立动量方程和几何方程、物理方程、边界条件构造等效积分弱形式方程。

动量方程：

几何方程：εij＝luij(2)

物理方程：σij＝dεij(3)

边界条件：

式中：σij表示应力分量，εij表示应变分量，ρ为密度，bi为体积力，l为计算微分算子，d为弹性矩阵，nj表示边界法向量，ti为边界载荷力，为边界位移。

把式(2)、式(3)、式(4)带入式(1)，联立上述方程得到动量方程的等效积分弱形式方程：

上式中，δui,j为i方向位移对xj坐标求偏导，v为求解体积域，s为边界域，a为面积域，uij为ij方向的位移，ui为i方向位移，为i方向的加速度，为sσ边界域上的外力。

步骤6：构造位移矩阵，将所述位移场函数带入所述等效积分弱形式方程求解，得到等效内力和外力矩阵。

将重构的位移场函数u^r(x)带入等效积分弱形式方程，并将该方程写成矩阵形式得到下式：

式中：m为质量矩阵，为加速度场，f^int为等效内力矩阵，f^ext为等效外力矩阵。

步骤7：利用中心差分法对等效积分弱形式方程进行代数求解，得到不同时间步的形变和应力。

所述中心差分法将时间平均分为n个时间间隔，0，δt，…t时刻的位移、速度、加速度已知，求解t+δt时刻对应的解；

加速度核速度利用中心差分法表示为

式中，ut-δt(x)为离散颗粒在t-δt时刻的位移，ut(x)为离散颗粒在t时刻的位移，ut+δt(x)为离散颗粒在t+δt时刻的位移；

t+δt时刻的位移解答可以根据时间t时刻的运动方程得到，即为下式

式中，m、c和k分别代表影响域的质量矩阵、阻尼矩阵和刚度矩阵；ft是t时刻外力和；

由此可得到中心差分法的递推公式

若t与t-δt时刻的位移已知，则可以进一步求解出t+δt时刻的位移。

需要注意的是，该算法开始计算时，即t＝0时，需要知道u-δt(x)，为此利用和的计算公式可以得到

其中，u0(x)和可以在初始条件中设置，而可利用初始时运动方程得到，即为

利用步骤5中的几何方程，即式(2)，将不同时刻位移带入计算，得到形变，即应变，在利用步骤5中的物理方程，即式(3)求解，将应变带入计算得到应力。

图3是本发明中再生核粒子算法与有限元法实现结构线性静力学仿真的求解精度比较图。可见，再生核粒子方法大大提升了结构线性静力学仿真的求解精度和求解效率。

以上对本发明的具体实施例进行了详细描述，但其只是作为范例，本发明并不限制于以上描述的具体实施例。对于本领域技术人员而言，任何对本发明进行的等同修改和替代也都在本发明的范畴之中。因此，在不脱离本发明的精神和范围下所作的均等变换和修改，都应涵盖在本发明的范围内。