一种重型拖拉机前托架可靠性分析方法与流程

本发明涉及重型拖拉机智能制造，尤其涉及一种重型拖拉机前托架可靠性分析方法。

背景技术：

前拖拉机作为重型拖拉机中的关键零部件，向前与配重及配重架相连，向后连接发动机。在重型拖拉机服役过程中同时承受弯曲、扭转等多种载荷，极端工况非常复杂，所以对重型拖拉机前托架强度的校核至关重要。实际工程中，由于加工制造误差和环境的随机性等，重型拖拉机前托架结构中存在与载荷、材料属性、几何特性等相关的大量不确定因素，这些不确定因素将直接影响前托架的可靠性，严重威胁重型拖拉机的服役安全和使用人员的人身安全。因此，充分考虑这些不确定因素的重型拖拉机前托架可靠性研究工作具有非常重要的工程意义。目前，针对托架的分析方法主要包括蒙特卡罗模拟方法(mcs)和一阶可靠性分析方法(form)等。mcs方法是一种被广泛使用的方法，但由于其需要基于大量样本来准确估计结构可靠性，导致其计算效率低下和成本高昂。form方法虽然可以减少模拟的样本数量，但其需要多次迭代和梯度计算。重型拖拉机控制系统精度更高、工作工况更极端、非线性程度更高。因此，提出一种适应于重型拖拉机前托架高效稳健的可靠性分析方法非常必要。

技术实现要素：

针对上述效率低、耗时长等问题，本发明提出了一种重型拖拉机前托架可靠性分析方法。从而可以高效求解重型拖拉机前托架的可靠性，提高经济效益。

根据本发明的一个方面，提供一种重型拖拉机前托架可靠性评估方法，所述方法包括如下步骤：

第一步：根据重型拖拉机前托架使用可靠性的定义，建立托架系统的功能函数z(x)，表达式为：

z(x)＝σ-σm(x)(1)

式中，σm(x)为托架系统使用工况中承受的最大应力，σ为托架的屈服强度，x为表示托架模型中的q维独立不确定性随机向量，拖拉机托架不确定性变量为材料的杨氏模量e、泊松比v及使用工况载荷p，即x＝{p,e,v}。

第二步：根据原点矩的定义，托架系统功能函数的前l阶原点矩表达式为：

式中e为数学期望算子，fx(x)表示x的pdf(概率密度函数)。

第三步：通过引入一维降维积分方法，即将随机模型转化为单个随机参量的子系统，将高维积分转换成了低维积分来求解，托架系统功能函数前四阶原点矩有如下表达式：

式中μj表示随机变量xj的均值，q表示随机变量的个数。通过二项式定理展开上式可重新表达如下：

定义：

由如下递归公式求解

其中，一维积分问题采用高斯积分求解：

式中，为xj的pdf。

第四步：为使得降维积分方法能够适用于任何连续分布，同时获得简洁的高斯积分表达式，需将随机变量转换为n(0,1/2)分布：

式中φ^-1[·]表示标准正态分布累积分布函数的反函数，表示xj的累积分布函数。αj的pdf表达式如下，其中e为自然常数：

第五步：不确定性变量转换后，一维积分表示如下：

采用gauss-hermite求积公式有：

式中wq和hq分别表示高斯积分权值和高斯积分点，r表示高斯积分点数，l＝4。

第六步：将一维积分公式从标准空间转换到原空间：

式中xjq可用下式表示：

式中代表xj的累积分布函数的反函数。

第七步：采用3个高斯积分点计算式(12)，则每个随机变量在每个高斯积分点均需调用一次式(13)，加上随机变量均为均值时，仅需调用3q+1次式(12)即可求解。

第八步：根据第七步求解的随机变量在不同高斯积分点在原空间的值，利用abaqus对托架进行有限元分析，求得其最大应力值σmi，i＝1,2,...,3q+1，即计算3q+1次托架承受的最大应力。

第九步：由第八步计算的σmi和托架系统功能函数计算zi，i＝1,2,...,3q+1，即第三步中的一维积分利用第二步中和mzl的计算公式得到托架系统功能函数的前4阶原点矩。

第十步：由原点矩求解中心矩k。

第十一步：将功能函数值z变换为均值为0、方差为1的标准随机变量y，变换公式为：

式中μz和σz分别表示托架系统功能函数的均值和标准差，公式如下：

第十二步：计算标准随机变量y的前四阶原点矩，计算公式为：

式中，i表示具体的阶数，取值为i＝0,1,2,3,4。

第十三步：定义随机变量y的信息熵为h[fy(y)]，信息熵具体表达式为：

式中，fy(y)表示随机变量y的概率密度函数，c＞0为常数；将标准随机变量y的前四阶原点矩作为约束条件，根据最大熵原理构造拉格朗日函数，拉格朗日函数表达式为：

其中，λi为第i阶对应的拉格朗日系数，λi＝(λ0,λ1,λ2,λ3,λ4)；

利用拉格朗日函数l对概率密度函数fy(y)求偏导数，使得在极值点处偏导数为0，求导过程具体表达式为：

第十四步：根据上一步求导过程，采用以下公式计算获得随机变量y的概率密度函数fy(y)，表达式具体为：

式中，a0,a1,...,ai为待定参数，

第十五步：根据随机变量y的概率密度函数fy(y)，计算出托架的可靠性表达式为：

其中，σz表示托架系统功能函数的标准差，μz表示托架系统的功能函数的均值

本发明的优势和有益效果在于以下几点：

1.本发明方法充分利用降维分解方法和高斯积分的特点，推导出子系统的统计矩组装成原系统的统计矩，避免了直接计算高维积分问题，兼具了高精度和高效率的双重优点。

2.本发明方法，在可靠性分析中相较于目前广泛使用的蒙特卡洛模拟法，在保证结果准确性的前提下，能够大幅度降低对样本规模的需求，仅需极少的样本数量便获得了较高的计算精度。

3.本发明方法，在可靠性分析中相较于传统的一阶可靠性分析法，利用的信息更多，不仅利用了随机变量的一阶矩和二阶矩，还进一步利用了随机变量的三阶及四阶中心矩的统计信息，虽然两者所需的样本数量均较少，但是本发明方法相对来讲能够获得更加准确的计算结果。

附图说明

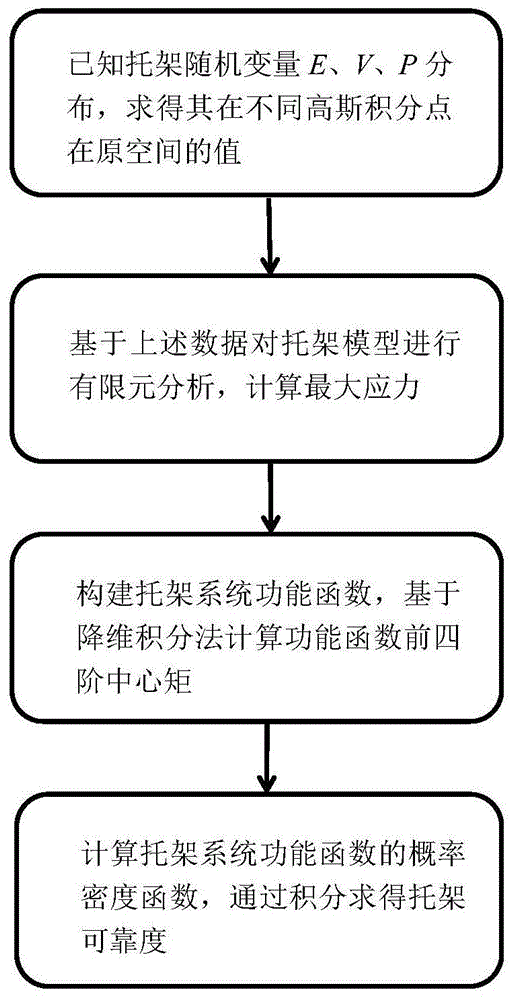
图1本发明方法的流程框图

图2托架有限元模型

图3托架失效概率随安全系数变化趋势

具体实施方式

本发明基于降维分解法、高斯积分理论和最大熵原理，提出了一种重型拖拉机前托架可靠性分析方法。本发明与传统的可靠性计算方法区别在于，将高维积分转换到低维空间积分，有效降低了高维高斯积分的计算难度。并能有效计算含有不确定性的系统的统计矩问题，兼具高精度和高效率的双重优点。

下面结合附图及具体实施例对本发明作进一步详细说明：

第一步：根据重型拖拉机前托架使用可靠性的定义，建立托架系统的功能函数z(x)，表达式为：

z(x)＝σ-σm(x)

式中，σm(x)为托架系统使用工况中承受的最大应力，σ＝310mpa，为托架的屈服强度。

第二步：由实际工程中重型拖拉机前托架的统计信息得到随机变量的分布如表1所示：

表1重型拖拉机前托架不确定性参数分布表

则托架系统功能函数z(x)的前4阶原点矩表达式为：

式中e为数学期望算子，fx(x)表示x的pdf。

第三步：通过引入一维降维积分方法，功能函数前四阶原点矩有如下表达式：

式中μj表示随机变量xj的均值，z(μ1,...,μj-1,xj,μj+1,...,μq)表示随机变量xj的响

应，由二项式定理展开有如下表达式：

定义

由如下递归公式求解

其中，一维积分问题采用高斯积分求解：

式中，为xj的pdf。

第四步：为使得降维积分方法能够适用于任何连续分布，同时获得简洁的高斯积分表达式，需将随机变量转换为n(0,1/2)分布：

式中φ^-1[·]表示标准正态分布累积分布函数的反函数，表示xj的累积分布函数。αj的pdf表达式如下：

第五步：不确定性变量转换后，一维积分表示如下：

采用gauss-hermite求积公式有：

式中wq和hq分别表示高斯积分权值和高斯积分点，r表示高斯积分点数，l＝4。

第六步：将一维积分公式从标准空间转换到原空间：

式中xjq可用下式表示：

式中代表xj的累积分布函数的反函数。

第七步：借助matlab软件，采用三个高斯积分点计算，得到随机变量在每个高斯积分点在原空间的值：

第八步：根据第七步求得的3个随机变量在3个不同高斯积分点原空间的值，及随机变量均为均值时，共计3*3+1＝10组数据如下：

利用abaqus对托架进行有限元分析，得到托架的最大应力值σmi，结果如下(单位mpa)：

托架系统功能函数的最大应力为(单位mpa)：

随机变量均取均值时功能函数取值z1＝102.9mpa。

第九步：由第八步计算的一维积分求解多维积分，利用第三步中和mzl的计算公式得到托架系统功能函数的前4阶原点矩mz1，mz2，mz3，mz4：

式中μj表示随机变量xj的均值，z(μ1,...,μj-1,xj,μj+1,...,μq)表示随机变量xj的响应，q＝3，l＝1，2，3，4；

mz1＝103.45

mz2＝1.1116e+04

mz3＝1.2362e+06

mz4＝1.4189e+08

第十步：根据第九步计算获得的托架系统功能函数的前4阶原点矩mz1，mz2，mz3，mz4，计算功能函数的前4阶中心矩kz1，kz2，kz3，kz4。中心矩和原点矩的关系表达式如下：

计算得：kz1＝103.45,kz2＝413.8269,kz3＝662.4742,

第十一步：将功能函数值z变换为均值为0、方差为1的标准随机变量y，变换公式为：

式中μz和σz分别表示托架系统功能函数的均值和标准差，

μz＝kz1＝103.45

σz＝(kz2)^1/2＝20.3427

第十二步：计算标准随机变量y的前四阶原点矩，计算公式为：

式中，i表示具体的阶数，取值为i＝0,1,2,3,4，计算得：

my0＝1；my1＝0；my2＝1；my3＝0.0787；my4＝3.0021。

第十三步：定义随机变量y的信息熵为h[fy(y)]，信息熵具体表达式为：

式中，fy(y)表示随机变量y的概率密度函数，c＞0为常数。

将标准随机变量y的前四阶原点矩作为约束条件，根据最大熵原理构造拉格朗日函数，拉格朗日函数表达式为：

其中，λi为第i阶对应的拉格朗日系数，λi＝(λ0,λ1,λ2,λ3,λ4)；

利用拉格朗日函数l对概率密度函数fy(y)求偏导数，使得在极值点处偏导数为0，求导过程具体表达式为：

第十四步：根据上一步求导过程，采用以下公式计算获得随机变量y的概率密度函数fy(y)，表达式具体为：

式中，a0,a1,...,ai为待定参数，

第十五步：根据随机变量y的概率密度函数fy(y)，计算出托架的可靠性表达式为：

其中，σz表示托架系统功能函数的标准差，μz表示托架系统的功能函数的均值。计算得到托架可靠性

第十六步：重复上述步骤计算托架在取不同安全系数下的可靠性及失效概率，结果如附图3所示。

本发明克服了现有技术中计算效率低下和成本高昂的技术问题，实现了高效求解重型拖拉机前托架的可靠性，提高经济效益。