一种新型网格正弦腔超混沌映射系统的制作方法

本发明涉及非线性系统
技术领域：
，具体是涉及一种新型网格超混沌映射系统。
背景技术：
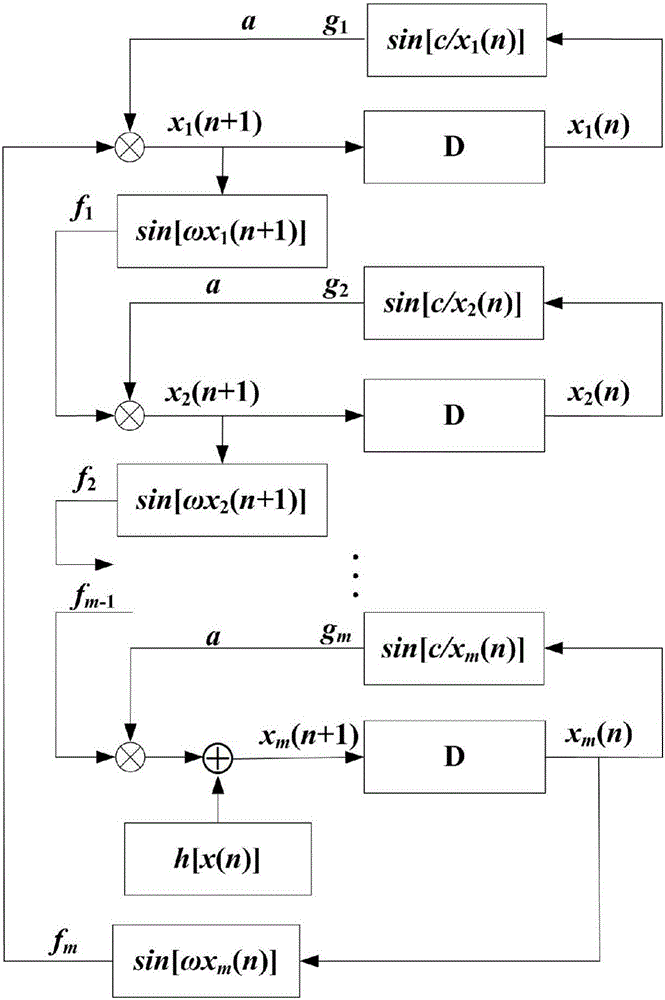
：现存的混沌映射可以被分为两类：第一类、一维混沌映射，一维混沌映射只有少量的参数和一个变量，比如Logistic映射，Tent映射，Chebyshev映射和正弦映射。其优势体现在实施效率和应用的简单性。因此，它们被大量应用于密码学以及混沌保密通信。但复杂性偏低，密钥空间小。随着互联网和云计算的发展，基于混沌加密的一维混沌映射已经不能保证信息传输的安全性，因为其轨道，参数和初始条件能被混沌信号预估技术所预测。第二类、高维混沌映射，对比一维混沌系统，高维混沌系统(尤其是超混沌系统)具有更复杂的结构和更好的混沌性能，超混沌系统是近年来混沌领域的研究热点。与混沌相比，超混沌具有2个及2个以上的Lyapunov指数。相轨迹在更多的方向上分离，具有更加复杂的动力学行为。随着一维正弦系统的发现，人们对其进入了广泛深入的研究，目前已有的研究成果主要是研究分析一维正弦类系统的动力学特性。然而，在实际的工程应用中许多物理系统是由两个变量甚至是多个变量描述，使得二维甚至是多维离散映射比一维离散映射具有更加复杂的非线性现象。通过已有的一维映射和方程构造出新的二维甚至是多维超混沌系统，有助于非线性物理系统的工程应用，为理论研究和应用实践提供范例。技术实现要素：本发明目的在于提供一种具有更好性能(吸引子相图清晰且具有丰富的动力学特性)的新型网格超混沌映射系统，具体技术方案如下：一种新型网格正弦腔超混沌映射系统，其构造包括以下步骤：第一步、建立一个基于闭环调制耦合的正弦离散非线性函数模型，获得m维控制系统的状态方程，具体为表达式8)：x1(n+1)=asin[ωxm(n)]sin[cx1(n)]x2(n+1)=asin[ωx1(n+1)]sin[cx2(n)]···xm(n+1)=asin[ωxm-1(n+1)]sin[cxm(n)]---8);]]>其中：x1、x2、x3、...、xm均为状态变量；a为振幅，ω为角频率，c为内部扰动频率，取值范围均为(0，+∞)；第二步、将第一步所得m维控制系统的状态方程与阶梯波函数进行组合，得到新型网格正弦腔超混沌映射系统的状态方程，具体为表达式9)：x1(n+1)=asin[ωxm(n)]sin[cx1(n)]x2(n+1)=asin[ωx1(n+1)]sin[cx2(n)]···xm(n+1)=asin[ωxm-1(n+1)]sin[cxm(n)]+h[x1(n)]---9);]]>其中：x1、x2、x3、...、xm均为状态变量，a为振幅，ω为角频率，c为内部扰动频率，且均为正实数；h[x(n)]为阶梯函数，其表达式为表达式10)或11)：h[x(n)]=aΣk=1N(sgn((Na)[x(n)]-2k)+sgn((Na)[x(n)]+2k))+asgn((Na)[x(n)]),N=even---10);]]>h[x(n)]=aΣk=1N(sgn((Na)[x(n)]+(2k-1))+sgn((Na)[x(n)]-(2k-1))),N=odd---11);]]>表达式10)和表达式11)中：x(n)为状态变量；N为网格正弦腔行数且为正整数；k为变量且为正整数；even代表偶数；odd代表奇数；sgn(u)为符号函数，具体为：u表示变量。以上技术方案中优选的，所述第一步中建立基于闭环调制耦合的正弦离散非线性函数模型的过程具体是：步骤1.1、设计一个具有一个控制参数ω的m维离散时间系统，具体为表达式1)：X(n+1)＝Af[xm(n),X(n+1),ω]1)；其中：X(n)＝[x1(n),x2(n),...,xm(n)]T，并且满足m≥2；A为一个m×m的控制矩阵；f[xm(n)，X(n+1)，ω]是一致有界的非线性反馈控制器，其取值为表达式2)：f[xm(n),X(n+1),ω]=f1[x1(n+1),ω]f2[x2(n+1),ω]···fm-1[xm-1(n+1),ω]fm[xm(n),ω]---2);]]>表达式2)中ω＝[ω,ω,...,ω]T；步骤1.2、简化表达式2)即得表达式3)：fi[xi(n),ω]＝sin[ωxi(n)],i＝1,2,...,m3)；步骤1.3、取A为含一个控制参数a的表达式4)：步骤1.4、根据表达式1)、2)、3)以及4)构造m维控制系统为表达式5)：X(n+1)＝BAf[xm(n),X(n+1),ω]5)；其中：B＝diag{g[x1(n)，c]，g[x2(n)，c]，...，g[xm(n)，c]}，m≥2，取g(·)为表达式6)：g[xi(n),c]＝sin[c/xi(n)]，i＝1,2,...,m6)；步骤1.5、根据表达式4)、5)以及6)即得系统方程表达式7)：根据表达式7)即得m维控制系统的状态方程为表达式8)：x1(n+1)=asin[ωxm(n)]sin[cx1(n)]x2(n+1)=asin[ωx1(n+1)]sin[cx2(n)]···xm(n+1)=asin[ωxm-1(n+1)]sin[cxm(n)]---8);]]>其中：a为振幅，ω为角频率，c为内部扰动频率，取值范围均为(0，+∞)。本发明新型网格正弦腔超混沌映射系统的核心是：先建立一个基于闭环调制耦合的正弦离散非线性函数模型，通过改变其系统参数，可得到不同数量的一维混沌吸引子，再与阶梯波函数组合，使得一维混沌吸引子向平面上延伸，从而得到网格超混沌吸引子，构造出了新型网格超混沌映射，采用本发明的技术方案，吸引子相图清晰，且具有丰富的动力学特性。除了上面所描述的目的、特征和优点之外，本发明还有其它的目的、特征和优点。下面将参照图，对本发明作进一步详细的说明。附图说明构成本申请的一部分的附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。在附图中：图1是本发明优选实施例1中单方向正弦腔的调制耦合模型图；图2是本发明优选实施例1中网格正弦腔的调制耦合模型图；图3(a)-(d)是实施例2中单方向正弦腔在不同参数下的混沌吸引子示意图；图4(a)-(d)是实施例2中二维网格正弦腔在不同参数下的混沌吸引子示意图；图5(a)-(b)是实施例2中ω＝π、c＝5、N＝3时随a变化的Lyapunov指数谱和分岔图；图6(a)-(b)是实施例2中a＝2、c＝5、N＝3时随ω变化的Lyapunov指数谱和分岔图；图7(a)-(b)是实施例2中ω＝π、c＝5、N＝3时随c变化的Lyapunov指数谱和分岔图；图8(a)-(b)是实施例2中ω＝π、c＝50、N＝4时随a变化的Lyapunov指数谱和分岔图；图9(a)-(b)是实施例2中a＝2、c＝50、N＝4时随ω变化的Lyapunov指数谱和分岔图；图10(a)-(b)是实施例2中ω＝π、c＝50、N＝4时随c变化的Lyapunov指数谱和分岔图。具体实施方式以下结合附图对本发明的实施例进行详细说明，但是本发明可以根据权利要求限定和覆盖的多种不同方式实施。实施例1：一种新型网格正弦腔超混沌映射系统，其构造包括以下步骤：第一步、建立一个基于闭环调制耦合的正弦离散非线性函数模型，详见图1，获得m维控制系统的状态方程，具体过程如下：步骤1.1、设计一个具有一个控制参数ω的m维离散时间系统，具体为表达式1)：X(n+1)＝Af[xm(n),X(n+1),ω]1)；其中：X(n)＝[x1(n),x2(n),...,xm(n)]T，并且满足m≥2；A为一个m×m的控制矩阵；f[xm(n)，X(n+1)，ω]是一致有界的非线性反馈控制器，其取值为表达式2)：f[xm(n),X(n+1),ω]=f1[x1(n+1),ω]f2[x2(n+1),ω]···fm-1[xm-1(n+1),ω]fm[xm(n),ω]---2);]]>表达式2)中ω＝[ω,ω,...,ω]T；步骤1.2、简化表达式2)即得表达式3)：fi[xi(n),ω]＝sin[ωxi(n)],i＝1,2,...,m3)；步骤1.3、取A为含一个控制参数a的表达式4)：步骤1.4、根据表达式1)、2)、3)以及4)构造m维控制系统为表达式5)：X(n+1)＝BAf[xm(n),X(n+1),ω]5)；其中：B＝diag{g[x1(n)，c]，g[x2(n)，c]，...，g[xm(n)，c]}，m≥2，取g(·)为表达式6)：g[xi(n),c]＝sin[c/xi(n)]，i＝1,2,...,m6)；步骤1.5、根据表达式4)、5)以及6)即得系统方程表达式7)：根据表达式7)即得m维控制系统的状态方程为表达式8)：x1(n+1)=asin[ωxm(n)]sin[cx1(n)]x2(n+1)=asin[ωx1(n+1)]sin[cx2(n)]···xm(n+1)=asin[ωxm-1(n+1)]sin[cxm(n)]---8);]]>其中：a是振幅，ω是角频率，c是内部扰动频率，取值范围均为(0，+∞)。表达式8)中所有的方程以闭环的形式连接起来，形成了一个反馈控制系统。第二步、将第一步所得m维控制系统的状态方程与阶梯波函数进行组合，得到新型网格正弦腔超混沌映射系统(其调制耦合模型详见图2)，其状态方程为表达式9)：x1(n+1)=asin[ωxm(n)]sin[cx1(n)]x2(n+1)=asin[ωx1(n+1)]sin[cx2(n)]···xm(n+1)=asin[ωxm-1(n+1)]sin[cxm(n)]+h[x1(n)]---9);]]>其中：x1、x2、x3、...、xm均为状态变量，a是振幅，ω是角频率，c是内部扰动频率，且均为正实数；h[x(n)]为阶梯函数，其表达式为表达式10)或11)：h[x(n)]=aΣk=1N(sgn((Na)[x(n)]-2k)+sgn((Na)[x(n)]+2k))+asgn((Na)[x(n)]),N=even---10);]]>h[x(n)]=aΣk=1N(sgn((Na)[x(n)]+(2k-1))+sgn((Na)[x(n)]-(2k-1))),N=odd---11);]]>表达式10)和表达式11)中：x(n)为状态变量；N为网格正弦腔行数且为正整数；k为变量且为正整数；even代表偶数；odd代表奇数；sgn(u)为符号函数，具体为u表示变量。当参数a，ω，N取不同数值时，可得到不同数目的网格正弦腔混沌吸引子。设x轴方向正弦腔的动态范围为2a，则y轴方向正弦腔的动态范围为2Na。若a为正整数，ω＝mπ，m＝1,2,3,...，则x轴方向上完整正弦腔的个数为2am，y轴方向上完整正弦腔的个数为N。当h[x(n)]取表达式10)时，可得到偶数行网格正弦腔：当h[x(n)]取表达式11)时，可得到奇数行网格正弦腔。实施例2：结合实施例1的方法构建二维正弦腔超混沌映射系统，详情如下：1、单方向正弦腔的系统方程为表达式1-1)：x(n+1)=asin[ωy(n)]sin[c/x(n)]y(n+1)=asin[ωx(n+1)]sin[c/y(n)]---1-1);]]>其中：x、y均为状态变量，a为振幅，ω为角频率，c为内部扰动频率，值得注意：xn和yn均不为零，否则此系统没有任何意义，且x0和y0均不等于kπ或设初始值x(1)＝0.3、y(1)＝0.3、n＝50000，在不同的取值参数下，利用Matlab进行数值仿真，可得到单方向多正弦腔混沌吸引子如图3(a)、图3(b)、图3(c)以及图3(d)，其中图3(a)-(d)是不同参数下的混沌吸引子(图3(a)-(d)的横坐标和纵坐标分别均为x(n)和y(n))，具体是：图3(a)是当a＝2、ω＝π、c＝2时的吸引子图；图3(b)是当a＝2、ω＝π、c＝3时的吸引子图；图3(c)是当a＝2、ω＝π、c＝5时的吸引子图；图3(d)是当a＝2、ω＝2π、c＝5时的吸引子图，结合图3(a)-(d)可知：单方向正弦腔混沌吸引子分布在一个较大的区域，且其密度线随着c的增加而下降，其系统的遍历性和随机性也随着c的增加而增强，正弦腔的个数也随着系统参数a和ω的变化而变化。2、二维网格正弦腔混沌系统的构造，具体过程是：为了更加清楚简单的分析此新型网格正弦腔的性能，选取二维网格正弦腔超混沌系统模型的方程为表达式1-2)：x(n+1)=asin[ωy(n)]sin[c/x(n)]y(n+1)=asin[ωx(n+1)]sin[c/y(n)]+h[x(n)]---1-2);]]>表达式1-2)中各参数的含义、初始条件及初始值均保持不变，利用Matlab进行数值仿真，得到的吸引子清晰，大小一致。通过改变参数a、ω以及c的值，来控制x轴方向上正弦腔的个数；通过改变N的值，来控制y轴方向上正弦腔的行数。因而可得到网格正弦腔吸引子，详见图4(a)、图4(b)、图4(c)以及图4(d)，其中图4(a)-(d)是不同参数下的混沌吸引子(图4(a)-(d)的横坐标和纵坐标分别均为x(n)和y(n))，具体是：图4(a)是当a＝2、ω＝π、c＝2、N＝2时的吸引子图；图4(b)是当a＝2、ω＝π、c＝5、N＝3时的吸引子图；图4(c)是当a＝2、ω＝2π、c＝5、N＝4时的吸引子图；图4(d)是当a＝3、ω＝π、c＝5、N＝5时的吸引子图，由图4(a)-(d)可知：网格正弦腔混沌吸引子同样分布在一个较大的区域，密度线会随着c的增加而下降，正弦腔的行数也随着N的变化而变化。3、二维网格正弦腔混沌系统的特性分析众所周知，李雅普诺夫指数和分岔图是动力学特性分析的重要指标。以三行网格正弦腔超混沌系统为例(即N＝odd的情况)，分析当系统参数变化时系统的动力学特性，仿真步长均为0.01，详情如下：(1)当ω＝π、c＝5、N＝3时，随幅度a变化的李雅普诺夫指数谱和与之对应的分岔图如图5(a)和图5(b)所示。幅度变化的范围a∈[0,5]，由图5(a)-(b)可知：在[0.701，1.118]的区间内存在两个正的Lyapunov指数；系统在该区间内处于超混沌状态。(2)当a＝2、c＝5、N＝3时，随频率ω变化的李雅普诺夫指数谱和与之对应的分岔图如图6(a)和图6(b)所示，由图6(a)-(b)可知：在区间[1.188，1.256]内有两个正的Lyapunov指数，表明系统处于超混沌状态；系统在ω∈[1.496，1.525]和ω∈[4.355，4.375]的区间内有明显的窄周期窗口，其余范围都是混沌状态。(3)当ω＝π、c＝5、N＝3时，随c变化的李雅普诺夫指数谱和与之对应的分岔图如图7(a)和图7(b)所示，由图7(a)-(b)可知：内部扰动频率c的变化范围是c∈[0,5]，除少数几个周期窗口外；系统在大部分区间范围内都处于混沌状态。以四行网格正弦腔超混沌系统为例(即N＝even的情况)，分析当系统参数变化时系统的动力学特性，仿真步长均为0.01，详情如下：(1)当ω＝π、c＝50、N＝4时，随幅度a变化的李雅普诺夫指数谱和与之对应的分岔图如图8(a)和图8(b)所示。幅度变化的范围a∈[0,5]，由图6(a)-(b)可知：系统处于全域混沌状态，在区间[0,4.558]内存在两个正的Lyapunov指数，处于超混沌状态。(2)当a＝2、c＝50、N＝4时，随频率ω变化的李雅普诺夫指数谱和与之对应的分岔图如图9(a)和图9(b)所示，由图9(a)-(b)可知：系统ω∈[0，5]的区间范围内基本处于超混沌状态。(3)当a＝2、ω＝π、N＝4时，随c变化的李雅普诺夫指数谱和与之对应的分岔图如图10(a)和图10(b)所示，内部扰动频率c的变化范围是c∈[0,5]。由图10(a)-(b)可知：除区间[0.712,0.810]∪[1.185,1.412]∪[1.611,2.001]有明显的周期窗口外；系统其他区域都处于混沌状态。采用本发明的设计原理，还可以可用于其他某些多方向分布网格状超混沌系统的设计，实用性强；通过设计单方向正弦腔混沌系统，在此基础上，结合阶梯函数得到新型网格正弦腔超混沌映射，得到的吸引子相图清晰且具有丰富的动力学特性。以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3