一种基于DPCM的三维量子图像压缩方法与流程

本发明涉及量子图像处理领域，尤其涉及一种基于DPCM的三维量子图像的压缩方法。

背景技术：

量子计算机靠量子比特来存储信息。与经典比特不同，量子比特有两个显著特点：一是叠加，二是纠缠。

叠加指得是一个量子比特可以同时存储0和1。量子计算机中的0和1与经典计算机中的0和1也有不同，量子计算机中叫做状态|0>和状态|1>。叠加态中既有|0>，又有|1>，表示为α|0>+β|1>，其中α²+β²＝1，且|0>和|1>所占的比重分别为α²和β²。多个量子比特也可以叠加，比如两个量子比特，可以同时存储|00>，|01>，|10>，|11>四个状态，表示为α|00>+β|01>+γ|10>+λ|11>，其中α²+β²+γ²+λ²＝1，且|00>，|01>，|10>，|11>所占比重分别为α²,β²,γ²,λ²。

纠缠指得是两个量子比特存储的状态之间互相影响的现象。比如两个量子比特所处的状态为那么如果第一个量子比特处在|0>状态，则第二个量子比特也一定处在|0>状态；如果第一个量子比特处在|1>状态，则第二个量子比特也一定处在|1>状态。此时，两个量子比特纠缠在一起，要么都处在|0>状态，要么都处在|1>状态。多个量子比特也可以纠缠。

叠加和纠缠带来的好处是量子计算机的高度并行性。在经典计算机上需要一个一个来处理的问题，在量子计算机上由于叠加存储在一起，只处理一次就可以解决。

近几年，量子图像处理逐渐成为量子计算领域的一个研究热点，指的是在量子计算机上进行图像处理。它有三个基本步骤：(1)将图像输入到量子计算机中，叫做量子图像制备。(2)用量子计算机处理图像。(3)通过量子测量得到处理后的结果。

目前，量子图像主要有以下几种制备方法：Qubit Lattice模型、RealKet模型、Entangled Image模型、Qubit Lattice模型]、FRQI模型、QSMC模型、FQRGI模型、NEQR模型和NAQSS模型等。其中，在NEQR量子图像制备方法中，一个尺寸为2ⁿ×2ⁿ、色深为q的图像需要用2n+q个量子比特来制备。其中的q个量子比特用来制备颜色信息，n个量子比特用来制备X坐标信息，另外n个量子比特用来制备Y坐标信息。用来制备颜色信息的量子比特的值中，|0>和|1>出现的比重根据图像的内容来设置，且与坐标信息纠缠在一起，即像素的颜色和坐标对应起来，以此制备整个图像。

由此可以看到，NEQR量子图像制备方法与经典图像制备方法有很大的不同。一个尺寸为2ⁿ×2ⁿ、色深为q的图像，在经典计算机上需要2ⁿ×2ⁿ×q个比特来制备，而在量子计算机上，只需要2n+q个量子比特来制备。

目前有一种三维图像的制备方法(NAQSS),该模型第一次对多维量子彩色图像实现表示、存储和检索。在该模型中，假定一个k维图像总共由2ⁿ个像素组成，我们使用n+1个量子比特来表示整个图像，其中使用n个量子位表示位置和颜色信息，剩余的一个量子位用于存储图像的截面信息(如果一个多维图像由m个截面组成，则这个剩余的一个量子位用于存储该截面的序列号)。如果位置态是|00L 0>，则其颜色值为θ₀；如果位置态是|00L 1>，则其颜色值θ₁；以此类推，直到位置信息为|11L 1>，颜色态是图像截面信息的序列号表示为|x_i>，如果某个像素恰好属于第i部分(i从0开始)，则该像素的量子值为的概率为0，量子值为的概率则为1。

NAQSS多维量子图像制备过程的主要困难是计算每个像素的概率，然后根据概率值来确定每个像素的位置和颜色信息。因此，它的主要前期工作是计算所有像素颜色值中的一个特定颜色值的百分比，然后根据这些值并使用旋转门来构造整个图像。因此当改变图像中任意一个像素值时，必须重新计算图像的所有像素的概率值。因此，很难在由NAQSS模型制备的图像上做任何关于位置或颜色信息的相关操作。

在对经典图像进行压缩时，几乎所有的数字图像压缩技术都是建立在发掘图像信息冗余度来实现的，预测编码就是其中一种很早就被提出并且较为简单实用的数字图像压缩技术，它是利用图像局部邻域像素的可预测性，去掉相邻像素之间的相关性和冗余度。实现时，用已传输的像素对当前像素进行预测，然后将真实值与预测值之间的预测误差进行编码处理和传输，这样就可以极大地减少存储与传输的空间和时间。而DPCM图像压缩技术就是上述的预测编码的一种，它的全称为差分脉冲编码调制，它编码的不是源图像像素，而是源图像像素与预测值之间的差值。其大致原理如下：设某图像中某一个像素点的位置是(m,n)，其像素值为f(m,n)，我们将其看做为参照像素点，f'(m,n)是由参照像素点(m,n)的周围邻近像素组合获得的预测值，则其差分数据e(m,n)就是f(m,n)与f'(m,n)的差值，显然e(m,n)是一个已经消除了相邻像素的相关性，能重建原始图像的一种数据压缩结果。如果用e_q(m,n)来表示差分数据e(m,n)量化后的编码值，则在压缩过程中，参照像素点周围邻近像素点的像素值就可以认作为e_q(m,n)，从而可将图像进行有效的压缩；而在解压缩过程中，参照像素点周围邻近像素点的像素值就可认作是参照像素点像素值与e_q(m,n)相加减所得到的值。该图像压缩方法实际上是一种有损压缩。

技术实现要素：

本发明的目的在于提供一种基于差分脉冲编码调制DPCM的三维量子图像压缩方法，便于今后进一步对三维图像处理算法的研究。

为了实现上述目的，本发明所采用如下的技术方案：

一种基于DPCM的三维量子图像的压缩方法，假设有一个大小为颜色灰度规模是2^q的三维量子图像，本发明采用三个坐标轴(X轴、Y轴和Z轴)和两个标志位|F>和|Q>来构造它，并使用二进制序列来表示坐标为(X,Y,Z)的像素的灰度值。

在实际中，很多三维图像的形状并不是完全规则的，因此对于一个形状不规则的三维图像，在空间内，并不是所有的点都能够被这个三维图像的像素所填充满。换句话说，对于一个空间大小为的不规则的三维图像，在空间内，一定有一些像素点在实际上是不存在的。因而需要用一个量子比特位表示标志比特|F>，以显示某一个位置点是否是一个真实存在的像素点。

在三维量子图像DPCM压缩过程中，我们需要一个量子比特位|Q>，来表示某个真实存在的像素点在压缩的过程中是否被用作是参照像素点。

针对三维量子图像的压缩方法包括：

步骤S1、准备q+n₁+n₂+n₃+2个初始态为|0>的量子比特。其中q个量子比特位用来表示像素的颜色值，n₁+n₂+n₃个量子比特位用来制备像素的位置信息，1个量子比特位作为图像的标志位|F>，用来存储该像素点是否为一个真实存在的像素点。另外剩余的1个量子比特位也作为标志位|Q>，用于存储压缩图像的参照像素点；

步骤S2、对于某个像素点，当|F〉的值为|0〉时表示该点不是一个真实存在的像素，反之，当值为|1〉时表示该点是一个真实存在的像素，此时运用n₁+n₂+n₃个Hadamard操作制备X、Y和Z坐标信息，再对该标志量子比特位|F〉施加一个n₁+n₂+n₃-CNOT门。Hadamard操作是量子计算中的一个基本操作，其作用是将|0>状态变为|0>和|1>各占的叠加态。n₁+n₂+n₃个Hadamard操作将所有存储坐标信息的n₁+n₂+n₃个量子比特全部变为|0>和|1>各占的叠加态，即叠加存储从00…00到11…11所有坐标信息。经过这一步的制备，会呈现出一个没有存储颜色值的空的三维图像；

步骤S3、将该的三维量子图像分割成若干个个小的三维图像单元。其中m₁≤n₁,m₂≤n₂,m₃≤n₃；

步骤S4、选取每个三维图像单元中的一个真实像素点作为参照像素点，此时我们将该参照像素点的标志量子比特位|Q>的值置为|1>，即对该标志量子比特位|Q>施加一个n₁+n₂+n₃-CNOT门；

步骤S5、对每个三维图像单元，除参照像素点之外，将所有剩余的真实像素点的颜色值与参照像素点的颜色值做对比。若其颜色值大于参照像素点的颜色值，记为A，反之，则记为B，其中A和B是两个不同的数，通常为了提高压缩比，A、B均取值于集合{0,1}；

步骤S6、接下来存储每个三维图像单元中参照像素点的颜色灰度信息。在三维图像单元中，对于其参照像素点(X,Y,Z)，本文使用q个量子比特位来表示该点的灰度值，使用来代表每一位量子比特。当时，表示将对该量子比特位不做任何操作，当时，表示在该量子比特位上施加一个n₁+n₂+n₃-CNOT控制非门。经过这一步的制备，所有三维图像单元中的参照像素点都已经存储了颜色值；

步骤S7、接下来存储每个三维图像单元中除参照像素点外的其他真实像素点的颜色灰度信息。对于一个像素点(非参照像素点)，根据步骤S5的所统计出的剩余像素颜色值与参照像素颜色值的对比结果，若其记录为A，则对表示该像素点的颜色值的q个量子比特位中的最低量子比特位施加一个n₁+n₂+n₃-CNOT控制非门；若其记录为B，则对该q个量子比特位不做任何操作。经过这一步的制备，就成功地将一个量子三维图像通过DPCM的方法实现高效的压缩。

本发明一种基于差分脉冲编码调制DPCM的三维量子图像压缩方法，首先将三维量子图像制备成一个没有存储颜色值的空图像；然后对要压缩的图像分割成较小的图像单元，记录图像单元的参照像素点；然后记录图像单元中除参照像素点之外剩余图像像素点颜色值与参照像素点的对比结果；然后存储图像单元中参照像素点的颜色值，并根据对比结果，存储每个图像单元中除参照像素点外像素的颜色信息。本发明中基于差分脉冲编码调制DPCM的三维量子图像压缩方法是一种有损压缩。

附图说明

图1是本发明的三维量子图像DPCM压缩方法的处理流程图；

图2是本发明中制备无颜色值空三维量子图像的过程图；

图3.a是一个2×3×2的三维图像实例；

图3.b是对3.a实例未进行DPCM图像压缩，所对应的量子电路图；

图4是对图3.a实例实行DPCM压缩后的量子电路图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清晰，下面将结合附图就实施例，对本发明进行进一步的详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

图1是本发明三维量子图像DPCM压缩方法的处理流程图。首先通过q+n₁+n₂+n₃+2个量子比特位制备出一个未存储颜色值的三维量子空图像；再将大小为的待压缩的三维量子图像分割成若干个大小为的三维量子图像单元，并在每个图像单元中选择一个真实参照像素点记录下来(若某个像素点被选作参照像素点，则将该像素点的|Q>量子比特位置为|1>，即施加一个n₁+n₂+n₃-CNOT控制非门)；然后在每个图像单元中对比参照像素点与其他剩余真实像素点的颜色值，并记录对比结果(若剩余像素点颜色值大于参照像素点颜色值，则记为A，反之，则记为B)；再然后通过q个量子位来存储三维量子图像参照像素点的颜色值，使用来代表每一位量子比特存储参照像素点的颜色值；最后根据上述图像单元内剩余像素点与参照像素点颜色值的对比结果来存储剩余像素点的颜色值信息，若对某像素点的记录为A，则将该像素点的存储颜色值的q个量子比特位中的最低量子比特位施加一个n₁+n₂+n₃-CNOT控制非门；若其记录为B，则对该q个量子比特位不做任何操作。由此，就成功地将一个量子三维图像通过DPCM的方法实现高效的压缩。

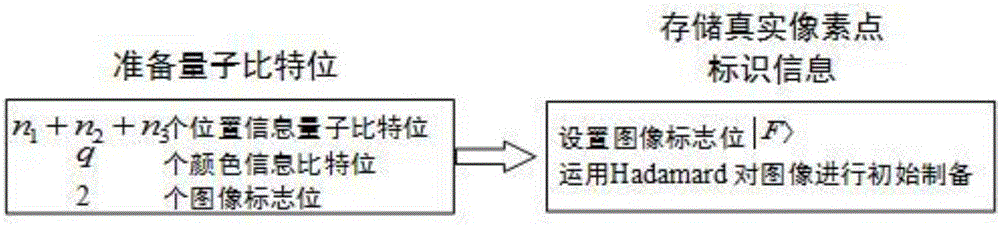
图2是本发明中制备无颜色值的空三维量子图像的过程图。首先，通过准备q+n₁+n₂+n₃+1个初始态为|0>的量子比特形成状态，其中q个比特位用来作为后续过程中存储像素的颜色值，n₁+n₂+n₃个量子位用来制备像素的位置信息，1个量子位作为图像的标志位。接着，设置图像标志位|F>，当|F>的值为|0>时表示该点不是一个真实存在的像素，反之当值为|1>时表示该点是一个真实存在的像素，此时运用n₁+n₂+n₃个Hadamard操作制备X、Y和Z坐标信息，并对该标志量子位施加一个n₁+n₂+n₃-CNOT门。经过这一步会将初始图像的从初始状态转化成所有像素都为空的空图像的状态。

图3.a是为更好的解释本发明中的DPCM压缩方法，所举例使用的一个2×2×2的三维图像。该图像中共真实存在4个像素，其位置颜色信息分别为：

位置信息为|000〉，颜色值为|255>，将颜色值化为二进制则为|11111111>；

位置信息为|010>，颜色值为|200〉，将颜色值化为二进制则为|11001000〉；

位置信息为|100〉，颜色值为|100〉，将颜色值化为二进制则为|01100100>；

位置信息为|011>，颜色值为|000>，将颜色值化为二进制则为|00000000>。

图3.b是若不用本发明中DPCM压缩方法，对一个量子三维图像制备存储的量子电路图。在本电路图中，可以看出，本图像共有4个真实像素(在|F>量子比特位上，一共有4个3-CNOT控制非门)，共使用12个量子比特，其中有8个颜色比特位1个标志比特位(|F>)，3个位置信息比特位(|X₀>、|Y₀>、|Z₀>)，共使用18个3-CNOT控制门。

图4是将图3.a的三维图像看做一个图像单元，并使用本发明中DPCM三维量子图像压缩的方法对图像单元进行压缩后的量子电路。假设图3.a刚好是一个大的三维图像中的一个小单元(2×2×2)，根据该图像单元中四个像素的颜色值，选择位置为|010>的像素点作为图像单元中的参照像素点，并将量子比特位|Q>的值置为|1>，即对它施加一个3-CNOT控制非门。剩余的三个像素与参照像素点做颜色值上的对比，其中位置信息为|000>的像素点将被记录为1，将该像素点颜色值最低量子比特位施加一个n₁+n₂+n₃-CNOT控制非门；位置信息为|100>和位置信息为|011>像素点将被记录为0，对颜色值量子比特位不做任何操作。在本电路图中，可以看出，共使用13个量子比特，其中有8个颜色比特位2个标志比特位(|F>、|Q>)，3个位置信息比特位(|X₀>、|Y₀>、|Z₀〉)，共使用9个3-CNOT控制门。由此看出量子电路中3-CNOT控制非门的数量明显减少，有效的实现了压缩。