一种基于相对熵理论的网络流量异常检测方法与流程
本发明涉及信息安全技术领域,涉及网络流量异常检测方法,具体是一种基于相对熵理论的网络流量异常检测方法。
背景技术:
:
随着计算机网络规模的不断扩大以及各类网络应用的不断深化,互联网已经融于人类的生产生活,逐渐成为人们生活的一部分,在给人们生活带来巨大方便的同时,网络拥挤和网络滥用等流量偏离其正常行为的流量异常情况时有发生,这些异常事件发作突然,并引起网络流量的剧烈变化,给网络安全和网络性能造成极大的伤害。而异常检测作为一种可以有效检测网络流量异常的方法,相关研究早已被广大学者和业界人士所重视,并取得了一定的研究成果。
熵是一种源于热力学的无序度量,表示系统微观状态的分布几率。信息熵则是熵在信息系统中的一种扩展,如果将信息源视为一组随机事件的集合,则热力学中微观状态的混乱度类同信息源的随机性不确定度,将热力学几率扩展到信息源信号出现的几率,就是信息熵。信息熵是对信息系统中随机事件不确定性程度的描述,标志着所含信息量的多少,信息熵作为一种复合型特征(区别简单特征,如计数特征、流量特征等),可以反映简单统计特征无法反映的内涵。当网络特征全部相同,取一个值时,表示特征的分布最集中,此时信息熵值取得最小值;当网络特征全取不同值时,表示特征的分布最为分散,信息熵值取得最大值,扩展到网络流量数据中,即在同一属性上,数据分布越集中的地方信息熵值越小,数据分布越分散的地方信息熵值越大。据研究发现,使用信息熵进行计算时,源/目的ip、源/目的端口和流持续时间等特征分布要比其他特征分布效果更好,并且这些特征本身具有强相关关系,可以有效的表征大规模网络流量的异常。以拒绝服务攻击(distributeddenialofservice,简称ddos)为例,它借助足够数量的傀儡主机,随机伪造大量的ip地址,在几乎同一时间开展拒绝服务攻击,向目标主机发送大量无用分组,引起源ip地址的分布更加分散,进而造成源ip地址信息熵突然增大,目的地址信息熵突然减小。
基于信息熵的网络流量异常检测依赖于流量的特征分布,可以提供比传统流量分析更细粒度的见解,近些年来引起了许多研究者的广泛关注。andersen、nychis等人针对网络流量报头特征和行为特征分布,测量出不同分布的熵在时间序列上的成对相关得分,结果表明基于熵的异常检测方法中,ip地址和端口分布之间具有强相关性,其他特征显示低相关性或无相关性;berezińskip、pawelecj等人通过捕获不同的流量特征,采用基于分组和基于流的方法,利用shannon熵和titchener熵以及参数化的renyi熵和tsallis熵四种信息熵算法分别实验,研究证明,当特征分布选择正确时,基于熵的检测方法优于大部分传统的异常检测方法,其中ip地址和端口以及持续时间的特征分布是最好的选择;国防科技大学教授郑黎明、邹鹏等针对传统异常检测系统分类器不同网络环境下不断变化的问题,提出了在hash直方图上基于增减式的在线svdd流量异常检测方法,结合多窗口关联检测算法结构,对提高分类器的检测效果和检测精度及减少算法的复杂度有很大的效果,但该方法需要大量的系统开销,且有一定的难度;清华大学信息网络工程研究中心专家朱应武和杨家海等通过对网络流量信息结构和网络流量规律的研究分析,利用正常网络流量的ip、端口等具有重尾分布和自相似特性等稳定的流量结构的特点,结合信息熵理论,对流量进行建模,将网络流量异常检测问题转换为基于svm的分类决策问题,提出了一种基于熵的支持向量机(supportvectormachine,svm)方法,实验结果表明,基于信息熵的svm方法更加简洁、高效,在网络流量小样本情况下,具有较高的检测效率和良好的检验精度,但在应对大规模突发性流量方面有一定的缺陷;西安理工大学张亚玲博士等人提出通过对网络流量进行统计分析,引入相对熵理论,通过对相对熵值多测度加权计算作为网络异常判断的依据,实现基于相对熵理论的网络异常检测,结果表明,该方法具有较低的误报率,但检测率效果不理想,而且需要计算大量的历史数据,另一方面,加权系数的设定比较困难;中国民航大学冯兴杰教授等人针对现有方法中模型弹性较差,无法适应动态网络变化的问题,在hurst指数分析的基础上,结合ewma和滑动窗口模型,提出一种基于动态阈值的网络异常检测,仅针对滑动窗口内的历史观测值进行分析,有效的避免了检测效率低的问题,但只对突发性流量具有较好的检测效果,对异常的类型检测方面也有不足。
技术实现要素:
本发明的目的是针对现有技术的不足,而提供一种基于相对熵理论的网络流量异常检测方法。这种检测方法能有效地检测出网络流量异常,并能解决低检测率和高误报率的问题,且能够适应动态变化的网络环境。
实现本发明目的的技术方案是:
一种基于相对熵理论的网络流量异常检测方法,包括如下步骤:
1)收集网络流量数据:从原始网络数据流中读取所需的网络流源端口的数据;
2)计算网络流量信息熵值:网络流量数据当作为离散信息源,将数据的特征当作一组随机事件,定义随机变量x={ni,i=1,2,...,n},表示网络流量数据中待分析的网络特征i发生了ni次,xi则表示该特征的具体值,那么信息熵的定义如下:
ni/s表示x取值特征值xi的概率,
设检测粒度为t,对检测粒度t内的网络流源端口的数据分布进行统计,将得到的统计结果通过公式(1)求出每个t内网络流源端口的数据分布的信息熵值,得到网络流源端口的数据分布情况的原始信息熵值序列e={ei,i=1,2,...,m},为下一步的检测分析准备数据;
3)构建滑动窗口模型:设数据流为一个不断增长的多维元组集合
4)计算滑动窗口内信息熵值的平均值:本方法中采用网络流量数据作为元祖集合的基本元祖。滑动窗口模型内预设w个正常网路流量数据,当有新的正常网络流量数据时,滑动窗口向前推移,加入最新的正常流量数据,并剔除最旧的正常流量数据;滑动窗口模型在任意时刻,仅仅考虑并处理包含在模型内的最近到达的w个数据,包含在滑动窗口内的w个数据即为有效元祖,有效元祖时标前的数据,称为过期元祖,且不参与数据的分析处理,正常信息熵值序列为ez={ezj,j=1,2,...,n},滑动窗口内包含最新的w个数据,求滑动窗口内数据的均值avg,其中
5)计算当前网络流量的相对熵值:信息熵是表示对不确定性程度的一种度量形式,当流量有异常发生时,网络流量在相关属性的信息熵值会与正常历史流量在该属性的信息熵值发生显著的差异性变化,对于这种差异性的变化,可以采用相对熵进行度量,相对熵,又称k-l散度,用信息量d(p,q)表示,用来度量两个概率分布p={p1,p2,...,pn}和q={q1,q2,...,qn}的相似程度,可表示为:
在信息熵的基础上,相对熵可以表示为对同一属性在不同状态下的特征分布的信息熵值比,用信息量i(p,q)表示,结合信息熵公式,相对熵可表示为:
其中,p代表当前检测的网络流量分布,q代表正常的历史网络流量分布,h(p)和h(q)分别代表当前检测的网络流量分布的信息熵值和正常的历史网络流量分布的信息熵值,相对熵值i(p,q)的一个重要性质是:i(p,q)≥0恒成立,且根据定义,i(p,q)越接近1,表示p和q越接近,反之则表示两个分布之间相差较大;当i(p,q)=1时,表示两个分布完全相同,此时,设u、v为上下限阈值,如果
i(p,q)∈[u,v](4)
则判定当前检测的网络流量正常;反之,则判定当前检测的网络流量发生异常,结合步骤4),当前信息熵值h(p)为ei,正常的历史网络流量分布的信息熵值h(q)为avg,根据公式(3),则相对熵值ei=ei/avg,若ei∈(u,v),则判定为正常;否,判定为异常;
6)检测下一粒度网络流量是否异常:
(1)若当前检测相对熵值无异常,将对应信息熵值放入正常信息熵值序列ez,滑动窗口向前推移一项,加入最新的正常熵值为活动数据,并剔除滑动窗口内最原始的一项为过期数据的活动数据,重新计算平均信息熵值avg,更新原有的avg,之后,跳转至步骤4),进行下一熵值的流量检测;
(2)若当前检测熵值为异常,则保持滑动窗口内数据、当前正常信息熵值的平均值avg不变,直接跳转至步骤4),进行下一熵值的异常检测。
所述检测粒度t为至少100。
所述网络特征i为源或目的ip、源或目的端口。
在实际应用中,人们常常关心的是最近一段时间的信息情况而不是所有的数据信息情况,这是因为久远的数据对最后的结果影响力比较小,而且在网络环境中,“正常流量”并非一个特定的状态,而是会随着网络环境以及相关因素的变化而不断更新的状态,因此,对于异常流量的判断也必须基于当前网络状态的正常基准值来确定。
这种检测方法将信息熵在原有的基础上,加以延伸,采用相对熵与滑动窗口结合的方法对网络流量进行异常的检测,检测率是指正确检测的异常数目占实际异常数目的百分比;误报率是指错误检测的异常数目占检测异常数目的百分比。
现实中,网络流量是随着网络环境以及相关因素的变化而不断更新的,比如,凌晨这个时段用户少,网络流量小,而工作时间等用网高峰期,网络流量大,这就给异常的检测带来偏差影响,针对这种情况,通过滑动窗口模型内的有效数据和当前检测数据相对熵值的变化可以准确的掌握当前数据流的状态,保证检测率的同时,有效降低误报率。
这种检测方法以信息熵算法为基础,与滑动窗口相结合,吸收相对熵的理论思想,通过对网络流量特征进行分析研究,建立熵值序列,结合滑动窗口模型,通过相对熵进行最后的检测。
这种检测方法能有效地检测出网络流量异常,并能解决低检测率和高误报率的问题,且能够适应动态变化的网络环境。
附图说明
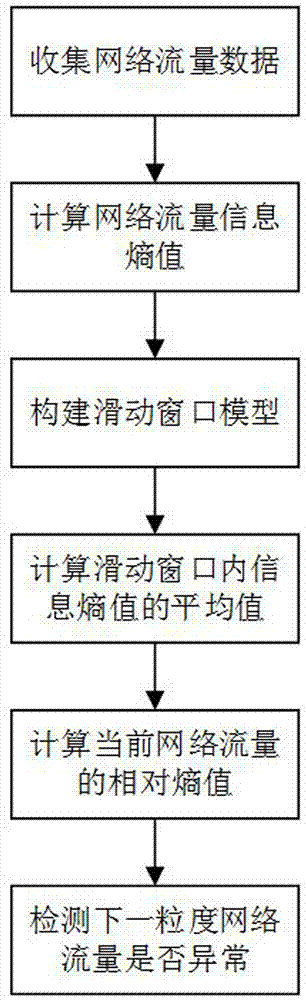
图1为实施例的方法流程示意图;
图2为实施例中滑动窗口参数取值变化对应的检测率和误报率曲线示意图;
图3为实施例中上下阈值参数取值变化对应的检测率和误报率曲线示意图;
图4为实施例中检测率与误报率变化曲线示意图。
具体实施方式
下面结合附图和实施例对本发明内容作进一步的阐述,但不是对本发明的限定。
实施例:
参照图1、一种基于相对熵理论的网络流量异常检测方法,包括如下步骤:
1)收集网络流量数据:从原始网络数据流中读取所需的网络流源端口的数据;
2)计算网络流量信息熵值:网络流量数据当作为离散信息源,将数据的特征当作一组随机事件,定义随机变量x={ni,i=1,2,...,n},表示网络流量数据中待分析的网络特征i发生了ni次,xi则表示该特征的具体值,那么信息熵的定义如下:
ni/s表示x取值特征值xi的概率,
设检测粒度为t,对检测粒度t内的网络流源端口的数据分布进行统计,将得到的统计结果通过公式(1)求出每个t内网络流源端口的数据分布的信息熵值,得到网络流源端口的数据分布情况的原始信息熵值序列e={ei,i=1,2,...,m},为下一步的检测分析准备数据;
3)构建滑动窗口模型:设数据流为一个不断增长的多维元组集合
4)计算滑动窗口内信息熵值的平均值:本方法中采用网络流量数据作为元祖集合的基本元祖。滑动窗口模型内预设w个正常网路流量数据,当有新的正常网络流量数据时,滑动窗口向前推移,加入最新的正常流量数据,并剔除最旧的正常流量数据;滑动窗口模型在任意时刻,仅仅考虑并处理包含在模型内的最近到达的w个数据,包含在滑动窗口内的w个数据即为有效元祖,有效元祖时标前的数据,称为过期元祖,且不参与数据的分析处理,正常信息熵值序列为ez={ezj,j=1,2,...,n},滑动窗口内包含最新的w个数据,求滑动窗口内数据的均值avg,其中
5)计算当前网络流量的相对熵值:信息熵是表示对不确定性程度的一种度量形式,当流量有异常发生时,网络流量在相关属性的信息熵值会与正常历史流量在该属性的信息熵值发生显著的差异性变化,对于这种差异性的变化,可以采用相对熵进行度量,相对熵,又称k-l散度,用信息量d(p,q)表示,用来度量两个概率分布p={p1,p2,...,pn}和q={q1,q2,...,qn}的相似程度,可表示为:
在信息熵的基础上,相对熵可以表示为对同一属性在不同状态下的特征分布的信息熵值比,用信息量i(p,q)表示,结合信息熵公式,相对熵可表示为:
其中,p代表当前检测的网络流量分布,q代表正常的历史网络流量分布,h(p)和h(q)分别代表当前检测的网络流量分布的信息熵值和正常的历史网络流量分布的信息熵值,相对熵值i(p,q)的一个重要性质是:i(p,q)≥0恒成立,且根据定义,i(p,q)越接近1,表示p和q越接近,反之则表示两个分布之间相差较大;当i(p,q)=1时,表示两个分布完全相同,此时,设u、v为上下限阈值,如果
i(p,q)∈[u,v](4)
则判定当前检测的网络流量正常;反之,则判定当前检测的网络流量发生异常,结合步骤4),当前信息熵值h(p)为ei,正常的历史网络流量分布的信息熵值h(q)为avg,根据公式(3),则相对熵值ei=ei/avg,若ei∈(u,v),则判定为正常;否,判定为异常;
6)检测下一粒度网络流量是否异常:
(1)若当前检测相对熵值无异常,将对应信息熵值放入正常信息熵值序列ez,滑动窗口向前推移一项,加入最新的正常熵值为活动数据,并剔除滑动窗口内最原始的一项为过期数据的活动数据,重新计算平均信息熵值avg,更新原有的avg,之后,跳转至步骤4),进行下一熵值的流量检测;
(2)若当前检测熵值为异常,则保持滑动窗口内数据、当前正常信息熵值的平均值avg不变,直接跳转至步骤4),进行下一熵值的异常检测。
所述检测粒度t为至少100,本例为100。
所述网络特征i为源或目的ip、源或目的端口。
具体地:
本实施例采用迄今为止网络安全审计研究人员使用最多的10%数据集(kddcup.data_10_percent_corrected)为实验的研究分析对象,检测粒度t为100,
对检测率dr和误报率fa定义如下:
dn,na,fd,df分别代表正确检测出的异常数目、实际存在的所有异常数目、误检测为异常的正常数据数目,检测的异常数目;
通过不断的调整u、v、w三个实验参数值对实验进行测试,并对结果进行分析,结果如图2-图4所示;
经过大量的实验测试发现,图2中,当u、v一定时,随着滑动窗口w的增大,模型的检测率先增加后减小,之后增加并稳定在区间[0.9,1]上,而误报率则随着w值的增大,先减小后增加,在图3中,随着对u、v、w三个参数值的不断调整,模型的检测率和误报率整体呈现增大趋势,当dr>0.936时,模型的检测率提升速度逐渐减慢,但误报率的增长速度加大,检测率和误报率的关系曲线如图4所示。在保证误报率在可接受范围内,检测率越高越好的前提下,综合分析可知,当检测率设在区间0.886~0.936之间时,检验结果比较理想,此时误报率在0.05~0.08之间,
通过分析测试结果可知,当相对熵上限值u=3.6,相对熵下限值取v=0.394时,dr=0.935,fa=0.055,结果相对理想,对kddcup9910%数据集(kddcup.data_10_percent_corrected)进行检测,结果如表1所示:
表1检测结果
由表1可知,本实施例的方法针对数据集中包含的四种异常类型均能有效的检测出来,其中以dos攻击检测结果最为优秀,检测率为97.8%,probe、u2r和r2l的检测率分别为78.74%、61.54%和75.84%,整体检测结果达到预期的效果。
为了证明实验改进的有效性,表2给出了3种不同网络流量异常检测的方法的结果,a代表一种基于分析视图的相对熵异常检测方法;b代表一种基于信息熵的异常检测方法;c代表基于信息熵的改进的k-maens网络流量异常检测方法;d代表本实施例方法:
表2不同检测方法异常检测结果比较
对比表中不同方法检测结果可知:检测率方面,方法a<b<c<d,误报率方面,方法b>c>d>a;相对于方法a、b、c三种算法,本实施例方法的检测率比方法a高出了8.5%,比方法b高出了2.3,比方法c高出0.8%;误报率方面,本实施例的方法比方法a高出0.5%、比方法b低3.1%、比方法c低1.96%。
综合分析表明,本实施例的方法在信息熵与相对熵理论的基础上,结合滑动窗口技术,采用最近影响力较大的正常流量数据,动态更新相对熵值,对网络流量进行异常检测,在保证低误报率的同时,最大限度提高了检测率,在总体上,对异常检测的性能有很大的改进。
- 还没有人留言评论。精彩留言会获得点赞!