一种基于分数阶自适应滑模控制的混沌系统同步方法与流程

本发明属于自动控制方法技术领域，涉及一种基于分数阶自适应滑模控制的混沌系统同步方法。

背景技术：

混沌是发生在确定系统中的貌似无规则运动，普遍存在于自然科学和社会科学中。混沌的研究是为发现系统混沌行为背后存在着的有序的、具有实用价值的信息，从而实现对混沌的利用。混沌同步作为混沌应用的重点课题，因其在保密通信等信息安全领域的巨大应用价值而备受关注。

混沌的同步从广义上将是一种混沌的控制，让被控混沌系统轨道按照目标混沌系统轨道运动，是一类控制问题。混沌同步的研究不局限于两系统间的同步，已拓展到多个系统间的同步，即复杂网络结点动力学的同步。另外，分数阶微积分作为整数阶微积分的推广，能够将原有整数阶系统中的丰富动力学行为拓展，能够更加真实地模拟自然界中的实际系统。

现阶段的研究一般基于整数阶微积分，实现混沌系统同步较慢。

技术实现要素：

本发明的目的是提供一种基于分数阶自适应滑模控制的混沌系统同步方法，能有效实现驱动混沌系统与其跟随系统的同步。

本发明所采用的技术方案是，一种基于分数阶自适应滑模控制的混沌系统同步方法，具体按照以下步骤实施：

步骤1，选择驱动混沌系统并计算该驱动混沌系统的状态信息量y1,y2,y3；

步骤2，计算该驱动混沌系统的跟随系统的状态信息量x1,x2,x3；

步骤3，根据该驱动混沌系统和其跟随系统的状态信息量求得误差系统e1,e2,e3；

步骤4，设置分数阶滑模面s(t)，保证驱动混沌系统在此滑模面上收敛；

步骤5，构建误差反馈同步控制率u1,u2,u3，添加自适应系数。

本发明的特点还在于，

步骤1中的驱动混沌系统的状态信息量y1,y2,y3具体为：

其中，u1为施加在y1上的控制量；τ是一个归一化处理后的时间函数；u2为施加在y2上的控制量；u3为施加在y3上的控制量，m为该系统非线性部分，q为误差系统的实际阶数。

步骤2中的跟随系统的状态信息量x1,x2,x3具体为：

步骤3中的误差系统e1,e2,e3具体为：

步骤4的设置分数阶滑模面s(t)的具体方法为：

步骤4.1，选择分数阶微积分的定义，具体为：

式中，q是分数阶微积分数且满足l-1＜q≤l，a为初值t为积分的下界，γ(·)是gamma函数。

步骤4.2，选取指定滑模面，具体为：

其中，i＝1,2,3，α的取值范围为0-1，q为误差系统的实际阶数，sgn为符号函数，公式中d^q-1是分数阶微积分算子，使用步骤4.1中的公式具体求出，步骤4.1中分数阶微积分的具体数值通过oustaloup滤波器方法求得。

步骤5中所述的构建误差反馈同步控制率u1,u2,u3，添加自适应系数具体方法为：

步骤5.1，构建误差反馈同步控制率：

u(t)＝-bx-g(y)+ax+f(x)-sgn(ei)|ei|^α

其中，b和a为驱动混沌系统和其跟随系统的系数矩阵，g(y)和f(x)为驱动混沌系统中的非线性项部分，当i＝1,2,3时，分别得到同步控制率u1,u2,u3；

步骤5.2，给步骤5.1求得的同步控制率中添加自适应系数，让系统根据误差大小更快的收敛，定义则，

式中，θ为自适应系数，n＝3。

本发明的有益效果是，一种分数阶滑模控制的方法，实现混沌系统的同步，能够根据误差信息实时反馈，根据误差信息自适应调节系统，实现驱动混沌系统与其跟随系统的同步。

附图说明

图1为本发明一种基于分数阶自适应滑模控制的混沌系统同步方法中跟随系统与驱动系统x1-y1时域波形；

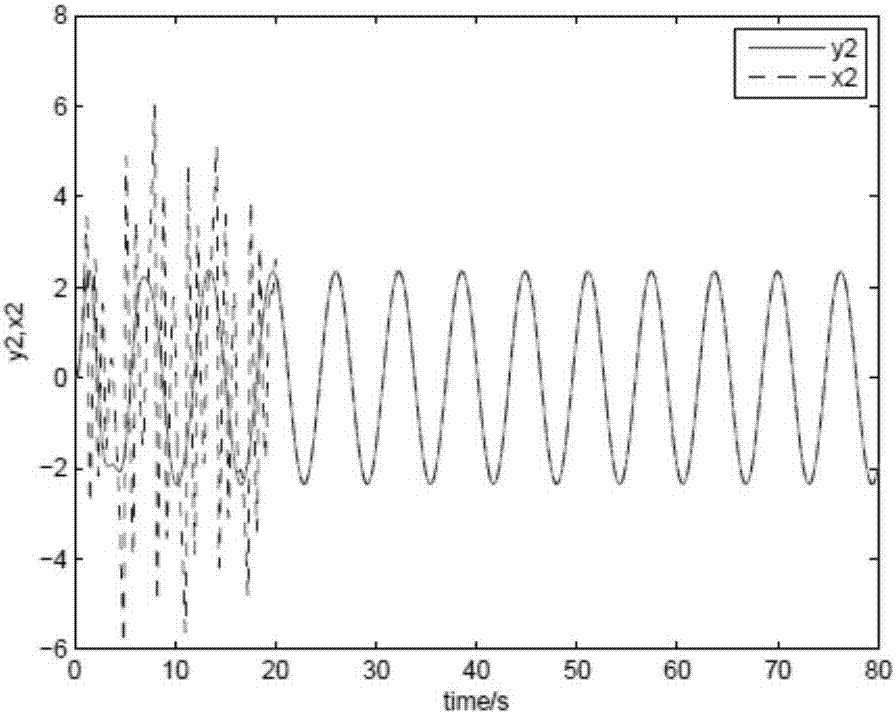
图2为本发明中一种基于分数阶自适应滑模控制的混沌系统同步方法跟随系统与驱动系统x2-y2时域波形；

图3为本发明中一种基于分数阶自适应滑模控制的混沌系统同步方法跟随系统与驱动系统x3-y3时域波形；

图4为本发明一种基于分数阶自适应滑模控制的混沌系统同步方法中误差系统时域波形。

具体实施方式

下面结合附图和具体实施方式对本发明进行详细说明。

本发明的一种基于分数阶自适应滑模控制的混沌系统同步方法，具体按照以下步骤实施：

取q＝0.95，m＝7，则：

步骤1，选择驱动混沌系统并计算该驱动混沌系统的状态信息量y1,y2,y3；具体为：

其中，u1为施加在y1上的控制量；τ是一个归一化处理后的时间函数；u2为施加在y2上的控制量；u3为施加在y3上的控制量。

步骤2，计算该驱动混沌系统的跟随系统的状态信息量x1,x2,x3；具体为：

步骤3，根据该驱动混沌系统和其跟随系统的状态信息量求得误差系统e1,e2,e3；具体为：

步骤4，设置分数阶滑模面s(t)，保证驱动混沌系统在此滑模面上收敛；具体方法为：

步骤4.1，选择分数阶微积分的定义，具体为：

式中，q是分数阶微积分数且满足l-1＜q≤l，a为初值t为积分的下界，γ(·)是gamma函数。

步骤4.2，选取指定滑模面，具体为：

其中，i＝1,2,3，α的取值范围为0-1，q为误差系统的实际阶数，sgn为符号函数，公式中d^q-1是分数阶微积分算子，使用步骤4.1中的公式具体求出，步骤4.1中分数阶微积分的具体数值通过oustaloup滤波器方法求得。

步骤5，构建误差反馈同步控制率u1,u2,u3，添加自适应系数；具体方法为：

步骤5.1，构建误差反馈同步控制率：

u(t)＝-bx-g(y)+ax+f(x)-sgn(ei)|ei|^α

其中，b和a为驱动混沌系统和其跟随系统的系数矩阵，g(y)和f(x)为驱动混沌系统中的非线性项部分，当i＝1,2,3时，分别得到同步控制率u1,u2,u3；

步骤5.2，给步骤5.1求得的同步控制率中添加自适应系数，让系统根据误差大小更快的收敛，定义则，

式中，θ为自适应系数，n＝3。

本发明的步骤4.2中q为误差系统的实际阶数，q取0.95。

根据李雅普诺夫稳定性定律，存在一个李雅普诺夫函数一直正定，对于本发明的控制率在所取滑模面对于误差系统可以实现正定，证明过程如下：

上述公式中bij为误差系统的系数矩阵，可以看出，李雅普诺夫函数满足以下关系：

化简后得：

可见化简后的等式恒为负数，由上述证明可以看出，李雅普诺夫函数的导数始终小于零，因此系统可以在滑模面上稳定。

通过matlab以及simulink仿真后，结果如图1-4所示，跟随系统以及驱动混沌系统所有变量都实现了混沌同步，在20秒系统开始介入控制率时，系统在2.5秒内收敛，体现了分数阶滑模控制具有较好的表现性能。