基于FPGA的独立边带调制信号解调方法与流程
本发明属于无线电监测领域,尤其涉及到的基于FPGA的独立边带调制信号解调方法,可用于接收机对ISB信号的解调应用。
背景技术:
在无线通信传输中,大体分为信号发射模块和信号接收模块,信号发射模块是将需要传递的基带信号转换成适合在信道中传输的功能模块,由于其包括较低频率分量,需要对其进行调制处理,将频率搬移到较高的频率上,提升发射效率;而信号接受模块是其逆过程,将已调信号解调出来,得到需要的基带信号。ISB信号是一种新型的信号调制方式,该调制信号的两个边带信号可以是不同频率的信号,相对于幅度调制信号、单边带调制信号、双边带调制信号,其中两个边带信号是完全相同的,其信息的传输能力更强,信道利用率更高,可以为日益拥挤的短波频段节约频率资源,具有较高的工程应用价值。ISB信号的频域表示直观、简明,如图1所示。目前已有的解调方法是基带边带滤波法,它是利用DSP强大的数据处理能力和高运算速度,对基带边带信号进行滤波的方法,分别滤出上下边带。假设上边带滤波器系数的实部是h1(n),虚部是h2(n),则上边带信号m(n)为:
m(n)=Re{[I(n)+jQ(n)]*[h1(n)+jh2(n)]}
=I(n)*h1(n)-Q(n)*h2(2)
同理,下边带信号m1(n)为:
m1(n)=Re{[I(n)+jQ(n)]*[h1(n)-jh2(n)]}
=I(n)*h1(n)+Q(n)*h2(2)
DSP要恢复出两路信号需要进行2次高阶滤波,并将滤波结果进行组合,最后得到解调结果。首先建立两条信号处理通路,通道0和通道1用来对上边带信号进行解调,通道2和通道3用来对上边带信号进行解调。以上边带通路为例,将通道0的本振载波设置为fc+f0,其中f0是上边带有效信号的中心频率。经过下变频后,上边带信号的中心频率被搬到零频,只要用一个低通滤波器进行滤波,就可以滤出上边带频谱。信号处理完毕后,将通道1输出的I1、Q1进行频率右移f0,并取实部就可以恢复出上边带信号。下边带通路处理过程与上边带类似,通道2和通道3时,本振载波应设置为fc-f0。
从上述分析可以看出,该方法充分利用了DSP固有的强大算法运算功能,如果用FPGA来实现时,会消耗大量的硬件资源,不利于工程实现。
技术实现要素:
本发明的目的是克服已有的基带边带滤波法对数据处理能力和高运算速度的强大需求,不易于FPGA中实现的缺点,提出的一种基于FPGA实现的新型ISB解调方法。
为实现上述目的,本发明是根据以下技术方案实现的:
基于FPGA的独立边带调制信号解调方法,其特征在于,包括以下步骤:
步骤S1:建立独立边带调制信号s(t)的数学表达公式:
式中,vU(t)和vL(t)分别为上、下边带信号,和分别为上、下边带信号的Hilbert变换,cos(wct)和sin(wct)为载波信号;
步骤S2:根据Hilbert变换原理,得到:
信号s(t)经过Hilbert变换后得到再经过Hilbert变换后得到-s(t);
在fc》fmax,的条件下,其中fc为信号的载波频率,fmax为调制信号的最大频率分量,得到下列表达式:
H[m(n)cos(wcn)]≈m(n)sin(wcn)
步骤S3:将ISB信号及其Hilbert变换信号输入第一通道中进行下变频操作,经过一组抽取滤波器后得到:
m1(t)=vL(t)+vU(t),
步骤S4:将ISB信号及其Hilbert变换信号输入第二通道中进行修正后的下变频操作,经过一组抽取滤波器后得到:
步骤S5:对得到的第二通道信号m2(t)进行Hilbert变换后,得到
步骤S6:对m1(t)和进行算法运算,分别求出上下边带信号:
上述技术方案中,所述步骤S2中的ISB信号的最大调制信号fmax在300kHz,而载波信号fc为30MHz以上。
上述技术方案中,步骤S3的抽取滤波器分段设置,结合Hilbert变换的带通范围,确定解调信号的频率范围。
上述技术方案中,步骤S4特征在于修正后的下变频是对换输入端口两端的信号,并且取反其中输出一端信号。
本发明与现有技术相比,具有如下有益效果:
本发明提出的基于FPGA实现的解调方法,是通过算法推导和工程实现验证过的,可以有效并准确的实现对ISB调制信号的解调,该方法同时还能用于SSB,USB和LSB信号的解调。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其它附图。
图1为本发明的独立边带信号的频谱图;
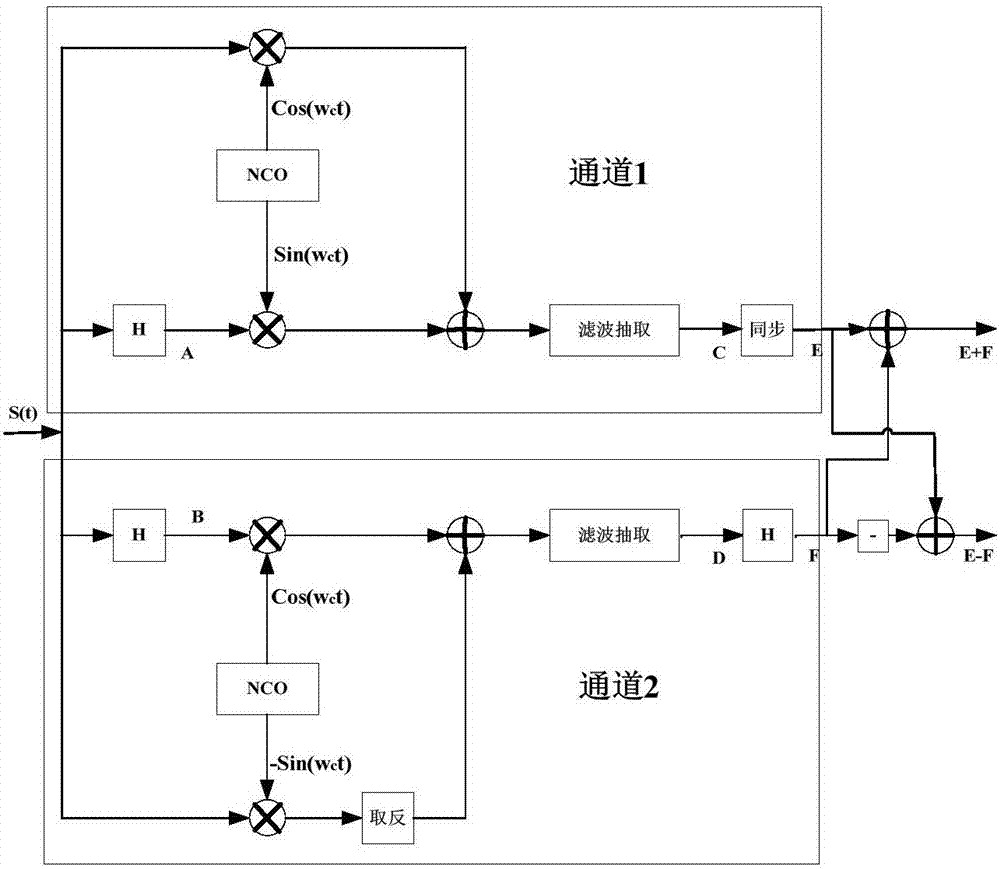
图2为本发明的ISB信号的相干解调算法原理图。
具体实施方式
为使本发明实施例的目的、技术方案和优点更加清楚,下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例是本发明一部分实施例,而不是全部的实施例。
在无线通信体系中,调制和解调是软件无线电中最具普适性也是最为关键的信号处理能力。为了便于信号发射,提高信道利用率、发射功率效率以及改善通信质量,人们研制出各种通信信号的调制方式。其中独立边带信号广泛应用于立体声广播、载波通信、无线电台、电视广播、卫星通信等领域。软件无线电几乎所有功能都将用软件实现,解调也不例外。软件无线电的解调一般采用数字相干解调的方法。数字相干解调法从原理上讲与模拟相干解调法一样。常见于模拟解调电路的一般相干解调法,当同频同相条件不满足时,解调信号就会出现严重失真。例如,在移动通信中,接受的信号由于受到严重的衰落,提取的出来的载波质量达不到要求,特别是在多普勒效应等引起的频偏环境下更是如此,由于正交解调法在一定程度上能克服以上这些弱点。因此,软件无线电的解调一般采用数字正交解调法。
目前已有的独立边带(ISB)解调算法是基带边带滤波法,该方法适用于DSP芯片,借助其强大的数据处理能力和高运算速度,对基带边带信号进行滤波,分别滤出上下边带,但是该方法需要大量的计算,不易于FPGA实现。
本发明的基于FPGA的独立边带调制信号解调方法,包含以下几个步骤:
步骤S1:建立独立边带调制信号s(t)的数学表达公式:
式中,vU(t)和vL(t)分别为上、下边带信号,和分别为上、下边带信号的Hilbert变换,cos(wct)和sin(wct)为载波信号;
步骤S2:根据Hilbert变换原理,得到:
信号s(t)经过Hilbert变换后得到再经过Hilbert变换后得到-s(t);
在fc》fmax,的条件下,其中fc为信号的载波频率,fmax为调制信号的最大频率分量,得到下列表达式:
H[m(n)cos(wcn)]≈m(n)sin(wcn)
步骤S3:将ISB信号及其Hilbert变换信号输入第一通道中进行下变频操作,经过一组抽取滤波器后得到:
m1(t)=vL(t)+vU(t),
步骤S4:将ISB信号及其Hilbert变换信号输入第二通道中进行修正后的下变频操作,经过一组抽取滤波器后得到:
步骤S5:对得到的第二通道信号m2(t)进行Hilbert变换后,得到
步骤S6:对m1(t)和进行算法运算,分别求出上下边带信号:
步骤S2中的ISB信号的最大调制信号fmax在300kHz,而载波信号fc为30MHz以上,条件fc》fmax是完全能够满足的,在实际使用过程中,只要保证fc是fmax的100倍以上,就完全没有问题。步骤S3的抽取滤波器分段设置,结合Hilbert变换的带通属性,确定解调信号的频率范围。步骤S4特征在于修正后的下变频是对换输入端口两端的信号,并且取反其中输出一端信号。
独立边带调制信号s(t)的数学表达公式:
式中,vU(t)和vL(t)分别为上、下边带信号,和分别为上、下边带信号的Hilbert变换,cos(wct)和sin(wct)为载波信号。图2中A、B两点处信号的数学表达公式:
滤波抽取模块主要功能是滤除杂散波、混有载波信号的高频已调信号和调节通带频率带宽,抽取倍数根据实际输出的解调信号和载波频率的比例关系以及Hilbert变换的带通性能确定,图2中C点处信号的数学表达公式:
后面经过同步模块,主要目的是为了同步2通道Hilbert变换的时序,得到图2中E点处信号的数学表达公式:
E=vU(t)+vL(t)。
滤波抽取模块主要功能是滤除杂散波、混有载波信号的高频已调信号和调节通带频率范围,抽取倍数由实际输出的解调信号和载波频率的比例关系以及Hilbert变换的带通性能确定,图2中D点处信号的数学表达公式:
后面经过Hilbert变换后,得到图2中F点处信号的数学表达公式:
F=-vU(t)+vL(t),
因此,上、下边带的解调信号数学表达公式分别为:
vU(t)=E-F
vL(t)=E+F°
本发明是基于软件无线电的核心思想,采用数字正交解调的基本思路,结合Hilbert变换性质,设计两路下变频通路,将所得信号进行算法运算,分别得到上下边带信号,解调信号灵敏度高,而且还适用于LSB/USB/SSB信号的解调应用。
虽然,上文中已经用一般性说明及具体实施例对本发明作了详尽的描述,但在本发明基础上,可以对之作一些修改或改进,这对本领域技术人员而言是显而易见的。因此,在不偏离本发明精神的基础上所做的这些修改或改进,均属于本发明要求保护的范围。
- 还没有人留言评论。精彩留言会获得点赞!