一种信噪比后滤波与特征空间融合的最小方差超声成像方法与流程

本发明属于超声成像技术领域，涉及一种信噪比后滤波与特征空间融合的最小方差超声成像方法。

背景技术：

超声成像中应用最为广泛的，也是最简单的波束形成技术即延时叠加算法(Delay And Sum，DAS)，它是根据阵元通道几何位置关系对所接收的回波信号进行延时量的计算，然后对延时后的数据对齐叠加。传统DAS算法复杂度低，成像速度快，但由于其采用固定窗函数加权导致主瓣宽度增加，分辨率较低。

近年来，为了提高波束形成算法的对比度和分辨率，自适应算法得到越来越多的研究。1969年Capon提出的最小方差(Minimum Variance,MV)波束形成算法是目前使用最为广泛的自适应算法。该方法依据保持期望方向增益不变，且使阵列输出能量达到最小的原则，通过动态地计算聚焦延时后的信号加权矢量，再将该矢量与输入信号相乘，提高了图像对比度和分辨率，但该算法的缺点是稳健性远不如传统的延时叠加算法，而且容易使有用信号相消，这在信噪比较低的情况下对图像质量有较大影响。因此，在最小方差算法的基础上算法分辨率、对比度和鲁棒性都还有很大的提升空间。

此外，由于介质的非均匀性，超声波在介质中的传播速度并非一成不变，而实际成像中往往使用固定常数减小计算复杂度，从而使图像分辨率和对比度有所下降。使用相干系数(Coherence Factor,CF)可以衡量超声波声束的聚焦质量，融合CF的波束形成算法可以减小栅瓣伪影。然而，当超声回波信号信噪比较低时，回波中噪声含量高，相干系数低，这将会导致图像整体亮度降低，目标幅值减小等问题。

综上所述，急需发明一种能够在低信噪比条件下提高图像分辨率、对比度，并且保持算法稳健性的波束形成算法，以全面整体提高超声成像质量。

技术实现要素：

有鉴于此，本发明的目的在于提供一种信噪比后滤波与特征空间融合的最小方差超声成像算法，该方法能够在低信噪比条件下提高图像分辨率、对比度以及波形形成鲁棒性，有效克服了传统自适应波束形成算法在低信噪比条件下，不能显著提高图像对比度和分辨率等问题，从而全面提高了超声图像的整体质量。

为达到上述目的，本发明提供如下技术方案：

一种信噪比后滤波与特征空间融合的最小方差超声成像算法，该方法包括以下步骤：

S1：对超声阵元接收的回波信号进行放大，AD转换和延时处理，以获得超声回波数据；得到聚焦延时处理之后的信号x(k)，x(k)表示为x(k)＝[x₁(k),x₂(k),…,x_N(k)]，其中N表示超声阵列的阵元个数，k表示为对应采样深度的采样时刻；

S2：将接收阵列依次划分为一个具有重叠阵元的子阵，然后对相应接收子阵的回波信号进行前后向平滑和对角加载处理，以获得样本协方差矩阵；

S3：对样本协方差矩阵进行特征分解，构造信号子空间；

S4：在期望信号子空间中，根据最小方差准则，计算得到特征空间最小方差波束形成权值；

S5：利用信号相干性设计后滤波器，并引入基于信噪比的噪声加权向量，得到信噪比后滤波系数；

S6：将自适应波束形成权值与信噪比后滤波系数融合，得到新的波束形成权值；

S7：使用信噪比后滤波与特征空间融合的最小方差波束形成权值对采样信号进行加权求和，得到自适应波束信号。

进一步，在S2中进行前后向平滑和对角加载处理，得到估计样本协方差矩阵，具体包括以下步骤：

S21：把N个阵元依次划分为阵元数目为L的子阵，并分别计算各个子阵的样本协方差矩阵R_l(k)，然后根据以下公式计算前向估计协方差矩阵

公式中表示第l个子阵的前向输出向量，为的共轭转置；

S22：定义为后向重叠向量，其中l＝1,2,…,N；与S21相似，可以通过下式计算得到后向估计协方差矩阵

公式中表示第l个子阵的后向输出向量，表示的共轭转置；

S23：通过以下计算公式计算前向估计协方差矩阵和后向估计协方差矩阵的求和平均，得到前后向估计协方差矩阵

S24：通过以下计算公式对前后向估计协方差矩阵进行对角加载，得到对角加载后的协方差矩阵

其中，Δ为空间噪声与信号功率之比，为信号的等效功率，I为单位矩阵。

进一步，在步骤S3中，通过下式对进行特征分解：

其中，λ_i为的特征值，且λ₁≥λ₂≥…≥λ_N，e_i为λ_i对应的特征向量，为e_i的共轭转置，特征向量矩阵E_M＝[e₁…e_M]；为E_M的共轭转置，特征值矩阵Λ_M＝diag[λ₁…λ_M]；将矩阵划分为期望信号子空间及与之正交的噪声子空间：

其中Λ_s为较大特征值组成的对角矩阵，Λ_n为较小特征值组成的对角矩阵；E_s为较大特征值对应特征向量，E_n为较小特征值对应特征向量，E_s^H，E_n^H分辨为E_s和E_n的共轭转置。

进一步，在步骤S4中，在期望信号子空间中，根据最小方差准则，计算得到特征空间最小方差波束形成权值，具体步骤如下：

S41：通过以下公式计算自适应波束形成权值：

其中a方向向量，w为自适应波束形成权值，为对应的逆矩阵；

S42：通过以下公式计算得到特征空间最小方差波束形成权值w_ESBMV：

其中E_s为较大特征值对应特征向量，E_s^H为其对应共轭转置，w为自适应波束形成权值；

进一步，在步骤5中，利用信号相干性设计后滤波器，并引入基于信噪比的噪声加权向量，得到信噪比后滤波系数，具体步骤如下：

S51：引入基于信噪比的噪声加权系数η：

其中，α为常数，P_s为信号功率，P_n为噪声功率；

S52：使用波束形成输出作为期望信号估计，得到新的后滤波系数L_pf为：

其中，w为自适应波束形成权值，w^H为w的共轭转置，x_n(k)为第n个阵元k时刻经过延时补偿后的信号，为x_n(k)的共轭转置；

进一步，在步骤6中，将自适应波束形成权值与信噪比后滤波系数融合，得到新的波束形成权值w_ESBMV-pf：

w_ESBMV-pf＝L_pfw_ESBMV

进一步，在步骤7中，使用信噪比后滤波与特征空间融合的最小方差波束形成权值对采样信号进行加权求和，得到自适应波束信号y(k)：

其中，表示w_ESBMV-pf的共轭转置，表示第l个子阵的输出向量。

本发明的有益效果在于：本发明采用了一种信噪比后滤波与特征空间融合的最小方差超声成像算法，该算法首先利用信号子空间划分将最小方差算法得到的权矢量投影到信号子空间中提高成像的对比度，然后基于信号相干性设计滤波器，并引入基于信噪比的噪声加权系数，使得算法对噪声的鲁棒性进一步增加。因此，本发明所提算法在低信噪比条件下改善图像对比度、分分辨率以及算法稳健性方面有较大提高，克服了传统自适应算法在信噪比较低条件下不能显著提高图像对比度和分辨率等问题。

附图说明

为了使本发明的目的、技术方案和有益效果更加清楚，本发明提供如下附图进行说明：

图1为本发明所述方法的流程图；

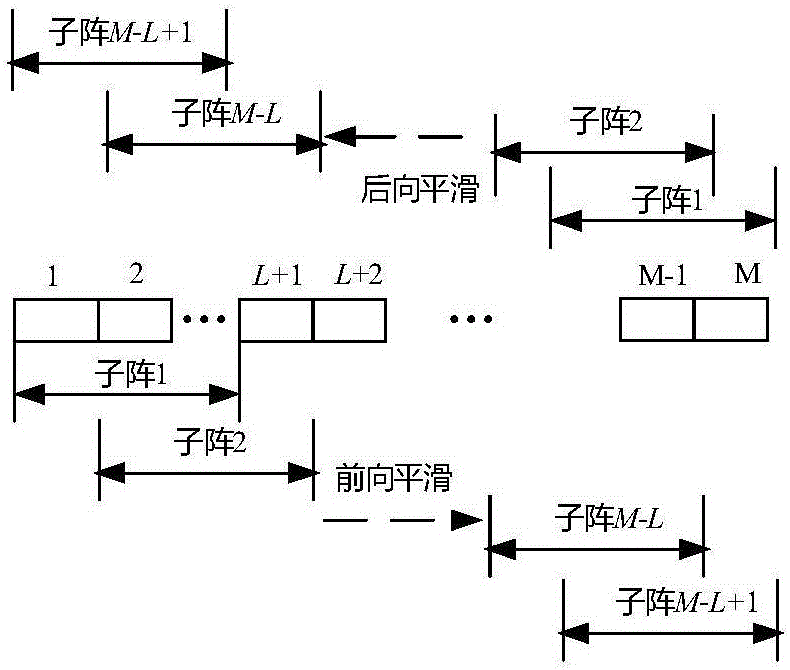
图2为前后向空间平滑算法示意图；

图3为5种算法点目标成像结果；

图4为55mm焦点处5种算法横向分辨率曲线图；

图5为5种算法不同深度处横向分辨率曲线；

图6为5种算法吸声斑目标成像结果；

图7为5种算法geabr_0数据成像结果；

图8为geabr_0实验70mm处散射点横向截面图。

具体实施方式

下面将结合附图，对本发明的优选实施例进行详细的描述。

图1为本发明的算法流程图，如图所示，本发明提供一种信噪比后滤波与特征空间融合的最小方差超声成像算法，包括以下步骤：

步骤S1：对回波信号进行放大和AD转换并进行延时聚焦处理，得到聚焦延时处理之后的信号x(k)，x(k)表示为x(k)＝[x₁(k),x₂(k),…,x_N(k)]，其中N表示超声阵列的阵元个数，k表示为对应采样深度的采样时刻。

步骤S2：将接收阵列依次划分为一个具有重叠阵元的子阵，然后对相应接收子阵的回波信号进行前后向平滑和对角加载处理，以获得样本协方差矩阵。图2给出了前后向空间平滑算法示意图，具体包括以下步骤：

S21：把N个阵元依次划分为阵元数目为L的子阵，L的取值上限为N/2，当L＝N/2时图像的分辨率最高，稳健性较差，考虑到本发明已采用前后向空间平滑滤波提高算法稳健性，因此子阵阵元数目取L＝N/2，并分别计算各个子阵的样本协方差矩阵R_l(k)，然后根据以下公式计算前向估计协方差矩阵

公式中表示第l个子阵的前向输出向量，为的共轭转置；

S22：定义为后向重叠向量，其中l＝1,2,…,N；与S21相似，可以通过下式计算得到后向估计协方差矩阵

公式中表示第l个子阵的后向输出向量，表示的共轭转置；

S23：通过以下计算公式计算前向估计协方差矩阵和后向估计协方差矩阵的求和平均，得到前后向估计协方差矩阵

S24：通过以下计算公式对前后向估计协方差矩阵进行对角加载，得到对角加载后的协方差矩阵

其中，Δ为空间噪声与信号功率之比，为信号的等效功率，I为单位矩阵。

步骤S3：对样本协方差矩阵进行特征分解，通过下式对进行特征分解，构造信号子空间：

其中，λ_i为的特征值，且λ₁≥λ₂≥…≥λ_N，e_i为λ_i对应的特征向量，为e_i的共轭转置，特征向量矩阵E_M＝[e₁…e_M]；为E_M的共轭转置，特征值矩阵Λ_M＝diag[λ₁…λ_M]；将矩阵划分为期望信号子空间及与之正交的噪声子空间：

其中Λ_s为较大特征值组成的对角矩阵，Λ_n为较小特征值组成的对角矩阵；E_s为较大特征值对应特征向量，E_n为较小特征值对应特征向量，E_s^H，E_n^H为其对应的共轭转置。

由于超声回波信号的主瓣能量主要集中在较大特征值所对应的特征向量中，因此，一般用大于最大特征值δ倍的特征值所对应的特征向量组成信号子空间，δ取值范围为0到1之间，在本实例中，用大于0.5倍最大特征值的特征值对角矩阵Λ_s和所对应的特征向量组成信号子空间其余的组成噪声子空间

步骤S4：在期望信号子空间中，根据最小方差准则，计算得到特征空间最小方差波束形成权值，具体包括以下步骤：

S41：通过以下公式计算自适应波束形成权值：

其中a方向向量，w为自适应波束形成权值，为对应的逆矩阵；

S42：通过以下公式计算得到特征空间最小方差波束形成权值：

其中E_s为较大特征值对应特征向量，E_s^H为其对应共轭转置，w为自适应波束形成权值，w_ESBMV为特征空间最小方差波束形成权值；

步骤S5：利用信号相干性设计后滤波器，并引入基于信噪比的噪声加权向量，得到信噪比后滤波系数，具体包括以下步骤：

S51：引入基于信噪比的噪声加权系数η：

其中，α为常数，P_s为信号功率，P_n为噪声功率；

S52：使用波束形成输出作为期望信号估计，得到新的后滤波系数为：

其中，w为自适应波束形成权值，x_n(k)为第n个阵元k时刻经过延时补偿后的信号，L_pf为后滤波系数；

η的取值范围为0～1，当回波信号信噪比较高时，η趋近于0，此时后滤波系数趋于1，波束形成输出在高信噪比条件下不受滤波系数影响；当回波信号信噪比较低时，η趋近于1，噪声系数相当于增大了期望信号能量，此时，后滤波系数的引入将减小栅瓣幅值。其中α影响噪声加权系数的斜率，较大的α值使得噪声加权系数曲线趋于二值函数，因此为避免噪声加权系数变化过快α取π。使用截止频率M₀将输入信号划分为信号功率P_s和噪声功率P_n，M₀的取值可以参考广义相干系数中截止频率选择方法，对点目标取0，吸声斑目标取3。

步骤S6：将自适应波束形成权值与信噪比后滤波系数融合，得到新的波束形成权值：

w_ESBMV-pf＝L_pfw_ESBMV

步骤S7：使用信噪比后滤波与特征空间融合的最小方差波束形成权值对采样信号进行加权求和，得到自适应波束信号y(k)：

其中，表示w_ESBMV-pf的共轭转置，表示第l个子阵的输出向量。

Field II是丹麦理工大学基于声学原理开发的一款超声实验仿真平台，其在理论研究上获得了广泛的认可和使用。为验证所提算法的有效性，利用Field II对超声成像中常用的点散射目标和吸声斑目标进行成像并利用实际实验数据进行成像对比实验。在点目标仿真实验中，设置两列横向间隔为2mm，纵向间隔为5mm的14个点目标，深度分布在35mm～65mm之间，采用发射定点聚焦和接收动态聚焦方式，发射焦点固定在55mm处，并在接收回波中加入一定噪声，设置图像的成像动态范围为60dB。同时，设一中心在35mm，半径为3mm的圆形区域吸声斑，外部随机分布着100000个散射点，在接收回波中加入一定噪声，并设定成像动态范围为80dB。实验所采用的阵元中心频率为3.33MHz，阵元数目为64个，间距为0.2413mm，采样频率为17.76MHz，声速为1500m/s，设成像动态范围为60dB。对上述三个实验目标采用延时叠加算法(DAS)，最小方差算法(MV)，特征空间最小方差算法(ESBMV)，融合相干系数的最小方差算法(ESBMV-CF)以及信噪比后滤波与特征空间融合的最小方差算法(ESBMV-PF)进行对比成像实验。

图3给出了5种算法点目标成像结果，从图3中可以看出DAS算法成像质量最差，分辨率最低，相比于其他4种算法横向伪影最多，两个散射点已经相互干扰难以区分。MV算法较DAS算法旁瓣有所降低，在焦点处散射点已基本能够区分，但在其他深度处横向伪影仍较多，分辨率有待提高。ESBMV算法在整个深度范围内可以明显分辨出相邻目标点。融合CF的ESBMV算法进一步减小了栅瓣影响。其中ESBMV-PF算法成像质量最优，对噪声鲁棒性最好，点目标主瓣宽度最小。

图4给出了55mm焦点处5种算法横向分辨率曲线图，图5给出5种算法不同深度处横向分辨率曲线，其中(a)为-6dB点目标处分辨率，(b)为-20dB点目标处分辨率。从图4中可以看出，DAS算法成像分辨率最差，主瓣宽度最宽且旁瓣等级最高。MV算法较DAS算法成像有所提高，其主瓣宽度和旁瓣等级都有所改善。ESBMV算法以及融合CF的ESBMV算法与DAS相比，主瓣宽度以及旁瓣等级已经改善明显，其-6dB主瓣宽度较MV分别减小了26.4％和29.0％，ESBMV-CF算法与ESBMV算法相比，主瓣宽度减小不多，但旁瓣幅度减小明显，对比度有所提高。其中ESBMV-PF算法主瓣最窄，其-6dB主瓣宽较MV算法减小69.6％，旁瓣等级最低，图像对比度最高。从图5可以看出5种算法横向分辨率随着深度的增加呈降低的趋势，由于焦点在55mm处，因此，在焦点处分辨率有所改善，分辨率曲线出现拐点。可以看出在不同深度处，ESBMV-PF算法分辨率均优于MV、ESBMV以及ESBMV-CF算法。

图6给出5种算法吸声斑目标成像结果，表1给出5种算法对比度。从图6中可以看出，DAS算法相比于其他算法成像效果最差，噪声抑制能力最弱，吸声斑内部存在噪声干扰严重。MV算法和ESBMV算法对噪声的抑制较DAS有所改善。由于CF对噪声较敏感，因而融合CF的ESBMV对噪声鲁棒性较ESBMV算法下降。ESBMV-PF算法噪声含量最小，算法旁瓣抑制能力最强。由表1可见，DAS算法对比度最低，仅为22.45dB，由于其只进行简单的叠加成像，计算复杂度低，因而背景方差最小，算法稳健性最好。MV算法提高了中心暗斑平均功率，但其外部平均功率也同时提高，对比度较DAS算法上升约2dB。ESBMV以及ESBMV-CF算法中心暗斑及背景功率分别在MV基础上有所提高，且可以看出当信噪比较低时，相干系数导致图像对比度下降。其中，ESBMV-PF算法中心平均功率上升最多，对比度较DAS，MV，ESBMV，ESBMV-CF算法分别提高了8.06dB、5.97dB、4.10dB、4.60dB，且背景区域方差低于ESBMV-CF。

表1 5种算法对比度

图7给出了5种算法geabr_0数据成像结果。图8给出geabr_0实验70mm处散射点横向截面图。从图7中可以看出，传统DAS算法成像效果最差，近场点目标受背景噪声干扰最为严重，采用自适应算法成像较DAS算法都好，其图像分辨率和对比度都有所改善，其中ESBMV-PF算法分辨率最高，对比度改善明显。从图8可以看出，ESBMV与MV算法分辨率相当且都高于传统DAS算法，融合CF的ESBMV算法进一步降低了旁瓣等级，提高了对比度。信噪比后滤波与特征空间融合的最小方差算法分辨率和对比度最高，其主瓣宽度最窄，最大旁瓣幅值最低。

最后说明的是，以上优选实例仅用以说明本发明的技术方案而非限制，尽管通过上述优选实例已经对本发明进行了详细的描述，但本领域技术人员应当理解，可以在形式上和细节上对其作出各种各样的改变，而不偏离本发明权利要求书所限定的范围。