一种新型主从式手术机器人控制方法与流程

本发明涉及一种遥操作机器人控制领域，特别涉及主从式遥操作手术机器人建模与控制技术，属于人机交互技术领域。

背景技术：

主从式遥操作手术机器人控制系统通常由一个主手操控台和若干个从手执行臂组成。从手执行臂安装于手术台旁边，在其末端可以安装内窥镜以及各种手术器械，通过微小创口到达病人体内病灶处。医生只需操作主手操控端，即可控制从手末端器械完成各种手术操作，为外科医生提供了传统手术的操作环境，可以协助医生完成更精细的手术动作，减少手术时由于疲劳产生的误操作或手部震颤造成的损伤。同时，因损伤小、愈合快为患者带来更理想的手术结果而得到广泛的应用。国外已有主从式手术机器人控制系统，但尚不具备动力学控制功能，且存在价格昂贵与不便于维护的问题。

技术实现要素：

有鉴于此，本发明的目的是提供一种新型主从式遥操作手术机器人控制方法，并通过力反馈技术提高手术安全性以及可靠性，让医生在实施遥操作手术时感受到远端执行机构与组织间的相互作用力。

本发明的目的是通过这样的技术方案实现的，一种新型主从式手术机器人控制方法，包括以下步骤：

s1、获取主手机器人各关节的位置信息和速度信息，利用构造法计算主手机器人的雅可比矩阵，经过主手机器人正运动学计算得到各关节在笛卡尔空间的位置信息和速度信息，并经过主手机器人正动力学计算得到各连杆与关节之间的力和力矩迭代方程；

s2、根据主手机器人各连杆质量及惯性张量计算惯性矩阵，根据已求得的各关节在笛卡尔空间的位置信息及力和力矩的关系信息计算各连杆的重力补偿系数，并将重力对各关节的力和力矩作用映射至各关节；

s3、根据末端受力情况，以及重力对各关节的作用，经过逆动力学计算得到各关节的期望力矩，并根据实时反馈的当前实际力反馈信息，引入内环/外环控制架构进行控制；

s4、根据主从手机器人比例及坐标映射关系得到从手机器人末端在笛卡尔空间的位置信息及速度信息，再经过从手机器人运动学位置逆解及基于逆雅可比矩阵变换得到从手机器人各关节的位置信息和速度信息，并计算各连杆与关节之间的力和力矩迭代方程；

s5、根据从手机器人各连杆质量及惯性张量计算惯性矩阵，根据已求得位置及力和力矩的信息对从手机器人进行重力补偿，实时获取从手执行端的力反馈信息，引入内环/外环控制架构进行控制。

进一步，在所述步骤s1与s4中，主手机器人与从手机器人的雅克比矩阵计算的构造法，上半部分下半部分其中，zi-1为第i个关节在基坐标系中表示的三维向量，on为末端执行器坐标原点在基坐标系中表示的三维向量，oi-1为第i个关节坐标原点在基坐标系中表示的三维向量，为雅可比矩阵的上半部分，为雅可比矩阵的下半部分。

进一步，在所述步骤s1与s4中，主手机器人与从手机器人各连杆与关节之间的力迭代方程

力矩迭代方程其中i为连体坐标系中的惯性张量，fi是由连杆i-1施加在连杆i上的力，为坐标系i+1到坐标系i的旋转矩阵，fi+1是由连杆i+1施加在连杆i上的力，mi为连杆i的质量，ac,i连杆i质心的加速度，gi重力引起的加速度在坐标系i中的表示，τi连杆i-1施加到连杆i的力矩，从坐标系i的原点到连杆i质心的向量，坐标系i相对于基坐标系的角加速度，ωi坐标系i相对于基坐标系的角速度，τi+1连杆i+1施加到连杆i的力矩。

进一步，在所述步骤s3中，各连杆的重力向量为g(q)＝[g1(q),...,gn(q)]^t,重力力矩对各关节的作用为力与力矩方程及各重力向量分量求得，g(q)重力引起的加速度在各坐标系中的向量表示，gn(q)为g(q)的分量，[]^t为矩阵的转置，g(k)为总势能p对关节k的位移qk的偏导数。

进一步，在所述步骤s3与s5中，内环控制方程为m(q)为惯量矩阵，aq表示待输入的加速度项，为离心项与科里奥项的表示，q为关节位置，为关节速度。

进一步，在所述步骤s3与s5中，外环控制方程为其中，k0和k1是对角矩阵，其对角元素分别由位置增益和速度增益组成。为参考加速度，k0与k1为增益矩阵，为位置增益，为加速度增益。

进一步，在所述步骤s4中，通过以下方法获得主从手机器人比例及坐标映射关系，

(1)首先通过进行主手机器人正运动学求解，得到主手机器人相对于主手机器人的基坐标系的位置变化为δdmb＝tmain(δθ1,...,δθ6)；θ1～θ6为关节位置，δθ1～δθ6为关节位置变化，为坐标系1到坐标系0的齐次变化矩阵，为坐标系2到坐标系1的齐次变化矩阵，为坐标系3到坐标系2的齐次变化矩阵，为坐标系4到坐标系3的齐次变化矩阵，为坐标系5到坐标系4的齐次变化矩阵，为坐标系6到坐标系5的齐次变化矩阵。

(2)然后通过δdmu＝tbu*δdmb关系式，将(1)中所述的δdmb从主手机器人的基坐标系转换到大地坐标系中，m表示主手，b表示大地坐标系，δdmu为主手机器人在大地坐标系中的位置变化，tbu为主手机器人的基坐标系相对于大地坐标系的变换矩阵。

(3)再通过主手机器人与从手器械臂间的比例变换关系δdsu＝k*δdmu，根据(2)中所述的δdmu得到从手器械臂相对于大地坐标系的位置变化δdsu，其中k为比例因子。

(4)再通过δdsd＝tu-d*δdsu关系式，根据tu-d和(3)中所述的δdsu，将从手器械臂相对于大地坐标系的位置变化转换为从手器械臂相对于显示器坐标系的位置变化δdsd，其中tu-d为从大地坐标系到显示器坐标系的变换矩阵。

(5)通过δdsc＝δdsd关系式，根据(4)中所述的δdsd，得到从手器械臂相对于从手持镜臂的位置变化δdsc。

(6)通过从手器械臂正运动学关系求得从手器械臂末端相对于持镜臂基坐标系(从手基坐标系)的变换矩阵；最后通过δdsb＝tslaveδdsc关系式，根据(5)中所述的δdsc得到从手器械臂相对于从手执行端基坐标系的运动；其中，θ1～θ6为关节位置，为坐标系1到坐标系0的齐次变化矩阵，为坐标系2到坐标系1的齐次变化矩阵，为坐标系3到坐标系2的齐次变化矩阵，为坐标系4到坐标系3的齐次变化矩阵，为坐标系5到坐标系4的齐次变化矩阵，为坐标系6到坐标系5的齐次变化矩阵。

由于采用了上述技术方案，本发明具有如下的优点：

本发明完成了主手与从手的运动学和动力学建模及主从手之间映射关系的理论推导，采用了重力补偿和内环/外环控制策略，采用模块化的程序架构完成了控制算法实现，高效的实现了主从式遥操作手术机器人控制系统，在控制的实时性、高速和高精度等方面具备较高水平。

附图说明

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作进一步的详细描述，其中：

图1为本发明遥操作手术机器人的控制系统结构示意图；

图2为本发明遥操作手术机器人的主手结构示意图；

图3为本发明遥操作手术机器人的从手程序框架图；

图4为本发明遥操作手术机器人的控制系统程序框架图；

图5为本发明遥操作手术机器人的控制系统建模方法流程图。

具体实施方式

以下将结合附图，对本发明的优选实施例进行详细的描述；应当理解，优选实施例仅为了说明本发明，而不是为了限制本发明的保护范围。

本实施例提供一种新型主从式遥操作手术机器人控制系统及方法，并通过力反馈技术提高手术安全性以及可靠性，让医生在实施遥操作手术时感受到远端执行机构与组织间的相互作用力。

一种新型主从式遥操作手术机器人控制系统，且通过下述的技术方案实现：

包括主手操控端、从手执行端及通讯系统；所述主手操控端包括主手机器人与主手操控端工业pc控制系统，所述从手执行端包括从手器械臂机器人、从手持镜臂机器人及从手执行端工业pc控制系统，所述通讯系统为以太网udp通讯系统。

主手机器人采用delta型7dof并联操纵机构，底层控制部分采用canopen总线式驱控一体式控制器，通过can转usb接口与主手操控端工业pc相连；

从手器械臂机器人采用7dof串联机构，底层控制部分采用canopen总线式驱控一体式控制器，通过can转usb接口与从手执行端工业pc相连；所述从手持镜臂采用6dof串联机构，底层控制部分采用canopen总线式驱控一体式控制器，通过can转usb接口与从手执行端工业pc相连。

所述控制系统包括以下部分：

机构参数模块，建立单连杆的结构体并根据手术机器人的结构参数及构造特征封装为机械类；

底层控制模块，将编码器读取函数、电机控制函数、i/o函数、状态监测函数封装为电机类；

运动控制算法模块，将运动学及动力学建模及求解、器械臂与持镜臂坐标变换、重力补偿及pid算法封装为控制类；

通信系统模块，将主从手间的udp通信部分封装为通信类；

文件操作模块，将文件读取及工作日志保存封装为文件类；

任务执行模块，将底层读取编码器及电机控制线程、运动学及动力学建模及求解线程、任务执行线程封装为任务类。

机构参数模块，包括连杆结构体、机构综合结构体。其中，连杆结构体包括连杆质量、质心位置、重力补偿系数、连杆惯量、电机惯量、dh参数、齐次变换矩阵、雅可比矩阵、连杆力矢量、连杆力矩矢量、正/逆运动学结果信息、正/逆动力学结果信息；机构综合结构体包括连杆数量、用户坐标系、世界坐标系、连杆坐标系、工具坐标系、关节位置/速度/加速度矢量、关节输出力矩矢量、重力矢量、机构全雅可比矩阵、机构惯量。

底层控制模块，包括编码器读取函数、电机控制函数、i/o函数、状态监测函数。

一种新型主从式手术机器人控制方法，包括以下步骤：

s1、获取主手机器人各关节的位置信息和速度信息，利用构造法计算主手机器人的雅可比矩阵，经过主手机器人正运动学计算得到各关节在笛卡尔空间的位置信息和速度信息，并经过主手机器人正动力学计算得到各连杆与关节之间的力和力矩迭代方程；根据编码器的信息反馈，通过主手机器人的逆运动学计算，实时监测各关节当前位置；

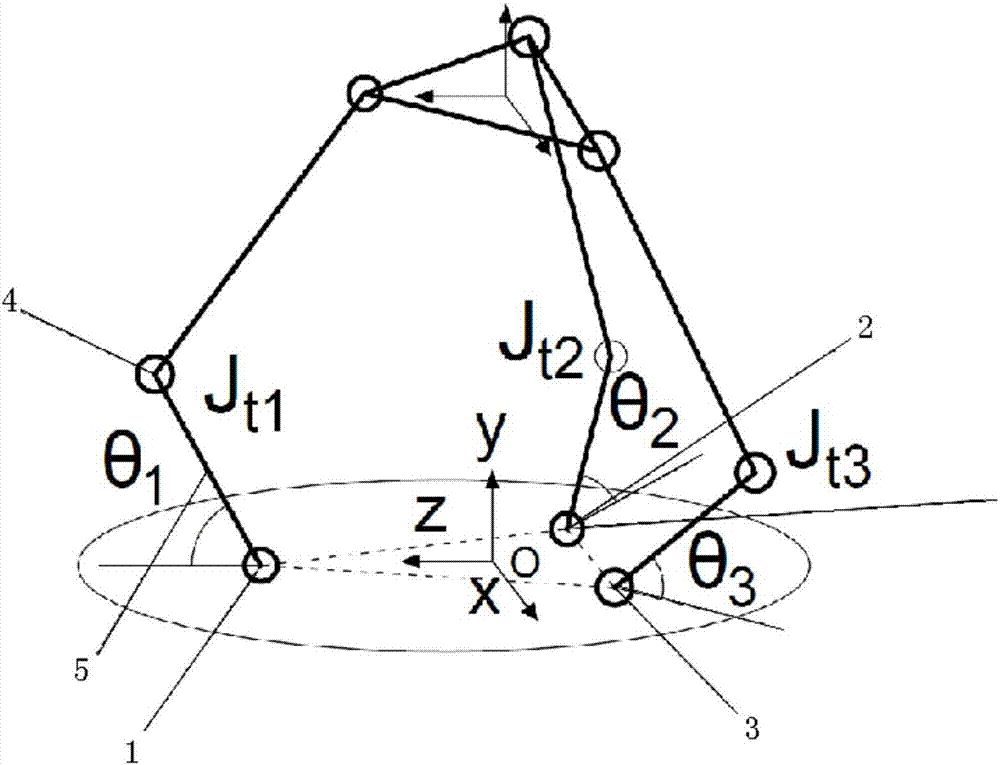
s1中主手机器人的运动学正解步骤为，首先根据三个关节的角度(θ1,θ2,θ3)可很容易求得delta并联机构三个杆链中间关节(jt1,jt2,jt3)的空间位置，然后再根据三个杆链的空间几何约束关系进行联合求解得到末端平台中心点的空间位置(xt,yt,zt)。

s1中主手机器人的运动学逆解步骤如下：θ1的求解过程为，首先将delta并联机构的三个杆链分别投影到三个关节的旋转平面上，然后根据delta并联机构末端小平台的三个顶点在各旋转平面上的投影位置可求解出各个杆链中间关节4(jt1,jt2,jt3)的位置坐标，进而可求解出关节一1的当前角度；θ2和θ3的求解过程为，分别将坐标系绕y轴旋转-120度和120度得到yoz’平面和yoz”平面，再分别将关节二2和关节三3的杆链5分别投影到新得到的yoz’和yoz”平面上，之后按照与关节一1的相同的求解步骤，求得关节二2和关节三3的当前角度。

s2、根据主手机器人各连杆质量及惯性张量计算惯性矩阵，根据已求得的各关节在笛卡尔空间的位置信息及力和力矩的关系信息计算各连杆的重力补偿系数，并将重力对各关节的力和力矩作用映射至各关节；

s3、根据末端受力情况，以及重力对各关节的作用，经过逆动力学计算得到各关节的期望力矩，并根据实时反馈的当前实际力反馈信息，引入内环/外环控制架构进行控制；

s4、根据主从手机器人比例及坐标映射关系得到从手机器人末端在笛卡尔空间的位置信息及速度信息，再经过从手机器人运动学位置逆解及基于逆雅可比矩阵变换得到从手机器人各关节的位置信息和速度信息，并计算各连杆与关节之间的力和力矩迭代方程；

s5、根据从手机器人各连杆质量及惯性张量计算惯性矩阵，根据已求得位置及力和力矩的信息对从手机器人进行重力补偿，实时获取从手执行端的力反馈信息，引入内环/外环控制架构进行控制。

在所述步骤s1与s4中，主手机器人与从手机器人的雅克比矩阵计算的构造法，上半部分下半部分其中，zi-1为第i个关节在基坐标系中表示的三维向量，on为末端执行器坐标原点在基坐标系中表示的三维向量，oi-1为第i个关节坐标原点在基坐标系中表示的三维向量，为雅可比矩阵的上半部分，为雅可比矩阵的下半部分。

在所述步骤s1与s4中，主手机器人与从手机器人各连杆与关节之间的力迭代方程

力矩迭代方程其中i为连体坐标系中的惯性张量，fi是由连杆i-1施加在连杆i上的力，为坐标系i+1到坐标系i的旋转矩阵，fi+1是由连杆i+1施加在连杆i上的力，mi为连杆i的质量，ac,i连杆i质心的加速度，gi重力引起的加速度在坐标系i中的表示，τi连杆i-1施加到连杆i的力矩，从坐标系i的原点到连杆i质心的向量，坐标系i相对于基坐标系的角加速度，ωi坐标系i相对于基坐标系的角速度，τi+1连杆i+1施加到连杆i的力矩。

在所述步骤s3中，各连杆的重力向量为g(q)＝[g1(q),...,gn(q)]^t,重力力矩对各关节的作用为力与力矩方程及各重力向量分量求得，g(q)重力引起的加速度在各坐标系中的向量表示，gn(q)为g(q)的分量，[]^t为矩阵的转置，g(k)为总势能p对关节k的位移qk的偏导数。

在所述步骤s3与s5中，内环控制方程为m(q)为惯量矩阵，aq表示待输入的加速度项，为离心项与科里奥项的表示，q为关节位置，为关节速度。

在所述步骤s3与s5中，外环控制方程为其

中，k0和k1是对角矩阵，其对角元素分别由位置增益和速度增益组成。为参考加速度，k0与k1为增益矩阵，为位置增益，为加速度增益。

进一步，在所述步骤s4中，通过以下方法获得主从手机器人比例及坐标映射关系，

(1)首先通过进行主手机器人正运动学求解，得到主手机器人相对于主手机器人的基坐标系的位置变化为δdmb＝tmain(δθ1,...,δθ6)；θ1～θ6为关节位置，δθ1～δθ6为关节位置变化，为坐标系1到坐标系0的齐次变化矩阵，为坐标系2到坐标系1的齐次变化矩阵，为坐标系3到坐标系2的齐次变化矩阵，为坐标系4到坐标系3的齐次变化矩阵，为坐标系5到坐标系4的齐次变化矩阵，为坐标系6到坐标系5的齐次变化矩阵。

(2)然后通过δdmu＝tbu*δdmb关系式，将(1)中所述的δdmb从主手机器人的基坐标系转换到大地坐标系中，m表示主手，b表示大地坐标系，δdmu为主手机器人在大地坐标系中的位置变化，tbu为主手机器人的基坐标系相对于大地坐标系的变换矩阵。

(3)再通过主手机器人与从手器械臂间的比例变换关系δdsu＝k*δdmu，根据(2)中所述的δdmu得到从手器械臂相对于大地坐标系的位置变化δdsu，其中k为比例因子。

(4)再通过δdsd＝tu-d*δdsu关系式，根据tu-d和(3)中所述的δdsu，将从手器械臂相对于大地坐标系的位置变化转换为从手器械臂相对于显示器坐标系的位置变化δdsd，其中tu-d为从大地坐标系到显示器坐标系的变换矩阵。

(5)通过δdsc＝δdsd关系式，根据(4)中所述的δdsd，得到从手器械臂相对于从手持镜臂的位置变化δdsc。

(6)通过从手器械臂正运动学关系求得从手器械臂末端相对于持镜臂基坐标系(从手基坐标系)的变换矩阵；最后通过δdsb＝tslaveδdsc关系式，根据(5)中所述的δdsc得到从手器械臂相对于从手执行端基坐标系的运动；其中，θ1～θ6为关节位置，为坐标系1到坐标系0的齐次变化矩阵，为坐标系2到坐标系1的齐次变化矩阵，为坐标系3到坐标系2的齐次变化矩阵，为坐标系4到坐标系3的齐次变化矩阵，为坐标系5到坐标系4的齐次变化矩阵，为坐标系6到坐标系5的齐次变化矩阵。

以上所述仅为本发明的优选实施例，并不用于限制本发明，显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。