基于现场拉拔试验的复合地层中预应力锚索轴力传递规律数学模型的构建方法

本发明涉及岩土工程领域，特别是涉及预应力锚索轴力传递规律数学模型的构建方法。

背景技术：

预应力锚索技术是一种被广泛地应用于基坑、边坡、巷道等岩土与地下工程领域的有效加固手段。预应力锚索的加固效果和工作性状对被加固体的安全与稳定以及经济效益具有重要影响，因此一直以来都是工程师和研究人员的重点关注对象。由于预应力锚索加固工程场地水文地质条件的隐蔽性及复杂性，影响预应力锚索加固效果和荷载传递规律的因素较多且其机理较为复杂。因此在研究预应力锚索的加固效果和荷载传递规律时采用能够反映预应力锚索实际工作状态的手段是保证研究成果可靠的前提。在不同的研究手段中，试验是较为可靠的研究手段。

近年来，基于试验手段研究锚索或预应力锚索荷载传递规律的装置和方法取得了一定的进展。例如中国专利文献cn111579229a公开了一种用于锚索预应力传递规律研究的试验装置及其工作方法，通过采用钢筒内填充砂浆模拟材料的设计，其可以使用钢筒来模拟围岩边界，用砂浆模拟材料来模拟围岩内部，合理的模拟出了锚索的固定环境；然后其通过在钢筒内设置锚索对中架来令锚索在钢筒内形成一个纺锤状结构，导致轴力减小，可以更加准确有效的检测到锚索位于钢筒内的预应力；最后其通过单孔穿心传感器、锚索轴力穿心传感器、磁通量传感器实现对锚索各个部位的预应力进行监测，通过监测数据对锚索预应力的传递规律进行研究；例如中国专利cn202073094u公开了预应力锚索连接器，利用锚索连接器的应用对现场监测轴力传递力非常方便，通过了解锚索轴力的传递，对设计和控制受力可作到实时监控。

然而，采用以上装置和方法均无法构建复合地层中预应力锚索轴力传递规律的数学模型。已有研究表明，预应力锚索的轴力传递规律与锚杆的轴力传递规律具有本质的区别，大量现场拉拔试验证实，锚杆轴力沿长度方向的分布近似呈高斯型正态曲线。由于预应力锚索的锚固段位于被加固体的深部，拉拔装置作用于岩土体表面的反向压力与注浆后岩土体自身的卸载对锚索锚固段外端的受力状态的影响可以忽略不计，因此预应力锚索锚固段外端的轴力最大，并逐步向岩土体深部衰减。事实上，如何利用预应力锚索现场拉拔试验获取的复合地层中预应力锚索的极限粘结强度构建轴力传递规律的数学模型，目前暂未见报道，这给复合地层中预应力锚索的设计优化带来了一定的困难。

技术实现要素：

本发明针对以上不足之处，提供了一种基于现场拉拔试验的复合地层中预应力锚索轴力传递规律数学模型的构建方法，该构建方法理论依据合理、操作简单、能够真实反映不同类型地层中预应力锚索极限粘结强度对轴力传递规律的影响效应，可方便地应用于复合地层中预应力锚索的二次设计优化。

为了实现上述内容，本发明提供以下技术方案：

本发明提供一种基于现场拉拔试验的复合地层中预应力锚索轴力传递规律数学模型的构建方法，所述构建方法的步骤为：

(1)对复合地层中预应力锚索的浆体-岩土体界面工作性状和荷载传递机理作出合理化假设与简化；

(2)推导整个预应力锚索锚固段均未达到塑性状态时的轴力传递规律方程t1(x)；

(3)推导上部地层中预应力锚索锚固段局部范围内达到塑性状态时的轴力传递规律方程t2(x)；

(4)推导上部地层中预应力锚索锚固段全部达到塑性状态时的轴力传递规律方程t3(x)；

(5)推导上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的轴力传递规律方程t4(x)；

(6)推导整个预应力锚索锚固段均达到塑性状态时的轴力传递规律方程t5(x)；

(7)开展第一组预应力锚索现场拉拔试验，并基于第一组预应力锚索现场拉拔试验结果计算上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度cupper；

(8)开展第二组预应力锚索现场拉拔试验，并基于第二组预应力锚索现场拉拔试验结果计算下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度clower；

(9)开展第三组预应力锚索现场拉拔试验，并基于第三组预应力锚索现场拉拔试验结果计算表征浆体-岩土体相对位移和浆体-岩土体剪切应力之间力学关系的刚度系数k；

(10)建立复合地层中预应力锚索轴力传递规律的数学模型。

进一步的，步骤(1)中所述假设与简化的内容具体为：

(1.1)随拉拔力的不断增大，复合地层中预应力锚索的浆体-岩土体界面工作性状逐渐由弹性状态向塑性状态过渡；

(1.2)当复合地层中预应力锚索的浆体-岩土体界面工作性状处于弹性阶段时，复合地层中预应力锚索的浆体-岩土体相对位移和复合地层中预应力锚索的浆体-岩土体剪切应力之间的力学关系符合虎克定律；

(1.3)当复合地层中预应力锚索的浆体-岩土体界面工作性状处于塑性阶段时，复合地层中预应力锚索的浆体-岩土体剪切应力随复合地层中预应力锚索的浆体-岩土体相对位移的增大保持不变；

(1.4)复合地层中预应力锚索的荷载传递机理符合弹簧-粘片力学模型。

进一步的，步骤(2)中所述整个预应力锚索锚固段均未达到塑性状态时的轴力传递规律方程t1(x)的推导过程为：

整个预应力锚索锚固段均未达到塑性状态时的浆体-岩土体剪切应力分布函数f1(x)表达式为：

对公式(1a)在0→x范围内进行积分，得到整个预应力锚索锚固段均未达到塑性状态时的轴力传递规律方程t1(x)为：

其中，p1^pullout是整个预应力锚索锚固段均未达到塑性状态时预应力锚索受到的拉拔力，范围为

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

是预应力锚索锚固段总长度；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

进一步的，步骤(3)中所述上部地层中预应力锚索锚固段局部范围内达到塑性状态时的轴力传递规律方程t2(x)的推导过程为：

假设从自预应力锚索锚固段始端算起，此时处于塑性状态的预应力锚索锚固段长度为满足的条件为：

上部地层中预应力锚索锚固段局部范围内达到塑性状态时的浆体-岩土体剪切应力分布函数f2(x)为：

对公式(2a)在0→x范围内进行积分，得到上部地层中预应力锚索锚固段范围内达到塑性状态时的轴力传递规律方程t2(x)为：

其中，是上部地层中预应力锚索锚固段局部范围内达到塑性状态时预应力锚索受到的拉拔力，范围为：

是上部地层中的预应力锚索锚固段长度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

与之间的关系为

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

进一步的，步骤(4)中所述上部地层中预应力锚索锚固段全部达到塑性状态时的轴力传递规律方程t3(x)的推导过程为：

此时处于塑性状态的预应力锚索锚固段长度＝上部地层中的预应力锚索锚固段长度

上部地层中锚固段全部达到塑性状态时的浆体-岩土体剪切应力分布函数f3(x)为：

将公式(3a)在0→x范围内进行积分，得到上部地层中锚固段全部达到塑性状态时的轴力传递规律方程t3(x)为：

其中，是上部地层中预应力锚索锚固段全部达到塑性状态时预应力锚索受到的拉拔力，范围为：

clower是下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

进一步的，步骤(5)中所述上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的轴力传递规律方程t4(x)的推导过程为：

此时处于塑性状态的预应力锚索锚固段长度满足的条件为：

上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的浆体-岩土体剪切应力分布函数f4(x)为：

将公式(4a)在0→x范围内进行积分，得到上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的轴力传递规律方程t4(x)为：

其中，是上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时预应力锚索受到的拉拔力，范围为：

公式(4c)；

clower是下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

进一步的，步骤(6)中所述整个锚固段均达到塑性状态时的轴力传递规律方程t5(x)的推导过程为：

此时处于塑性状态的预应力锚索锚固段长度＝预应力锚索锚固段总长度

整个预应力锚索锚固段均达到塑性状态时的浆体-岩土体剪切应力分布函数f5(x)为：

将公式(5a)在0→x范围内进行积分，得到整个预应力锚索锚固段均达到塑性状态时的轴力传递规律方程t5(x)：

其中，是整个锚固段均达到塑性状态时预应力锚索受到的拉拔力，

clower是下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

进一步的，步骤(7)中上部地层中锚固段浆体与岩土体之间的平均极限粘结强度cupper的计算过程为：

在第一组预应力锚索现场拉拔试验中，钻孔仅钻至上部地层中，预应力锚索锚锚固段仅位于上部地层中；第一组预应力锚索现场拉拔试验应加载至拉出破坏；上部地层中预应力锚索锚锚固段浆体与岩土体之间的平均极限粘结强度cupper计算式为：

其中，π是圆周率；

是第一组预应力锚索现场拉拔试验达到拉出破坏时的极限拉拔力；

dgr1是第一组预应力锚索现场拉拔试验的锚固段钻孔半径；

是第一组预应力锚索现场拉拔试验的锚固段长度。

进一步的，步骤(8)中下部地层中锚固段浆体与岩土体之间的平均极限粘结强度clower的计算过程为：

在第二组预应力锚索现场拉拔试验中，钻孔钻至下部地层中，预应力锚索锚固段仅位于下部地层中；第二组预应力锚索现场拉拔试验应加载至拉出破坏；下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度计算式为；

其中：π是圆周率；

是第二组预应力锚索现场拉拔试验达到拉出破坏时的极限拉拔力；

dgr2为第二组预应力锚索现场拉拔试验的锚固段钻孔半径；

为第二组预应力锚索现场拉拔试验的锚固段长度。

进一步的，步骤(9)中表征浆体-岩土体相对位移和浆体-岩土体剪切应力之间力学关系的刚度系数k的计算过程为：

在第三组预应力锚索现场拉拔试验中，钻孔钻至下部地层中，预应力锚索锚固段位于上部地层和下部地层中；第三组预应力锚索现场拉拔试验不需要加载至拉出破坏，但应至少加载至上部地层中预应力锚索锚固段局部范围内开始达到塑性状态；表征浆体-岩土体相对位移和浆体-岩土体剪切应力之间力学关系的刚度系数k计算式为：

其中：π是圆周率；

dgr3是第三组预应力锚索现场拉拔试验的锚固段钻孔半径；

etest3是第三组预应力锚索现场拉拔试验中预应力锚索钢绞线的弹性模量；

atest3是第三组预应力锚索现场拉拔试验中预应力锚索钢绞线的横截面面积；

是第三组预应力锚索现场拉拔试验的锚固段长度；

β是第三组预应力锚索现场拉拔试验获得的荷载-位移曲线的弹性阶段的斜率；

是第三组预应力锚索现场拉拔试验的自由段长度。

进一步地，将所获取的相关参数代入t1(x)、t2(x)、t3(x)、t4(x)、t5(x)中，即建立起复合地层中预应力锚索轴力传递规律的数学模型。

本发明具有以下有益效果：

(1)本发明只需开展常规的预应力锚索现场拉拔试验，且在预应力锚索现场拉拔试验过程中不需要在预应力钢绞线上粘贴应变片，因此彻底解决了在预应力钢绞线上粘贴应变片较为困难以及钢绞线上应变片测值与实际偏差较大的缺陷，具有节约工程成本、省时省力、计算精度高的优点；

(2)本发明将预应力锚索现场拉拔试验的优势和弹簧-粘片理论模型的优势相结合，能够真实考虑不同类型地层中预应力锚索极限粘结强度对轴力传递规律的影响效应，可方便地应用于复合地层中预应力锚索的二次设计优化；

(3)本发明能够真实反映不同类型地层中预应力锚索极限粘结强度对轴力传递规律的影响效应，可方便地应用于复合地层中预应力锚索的二次设计优化。

附图说明

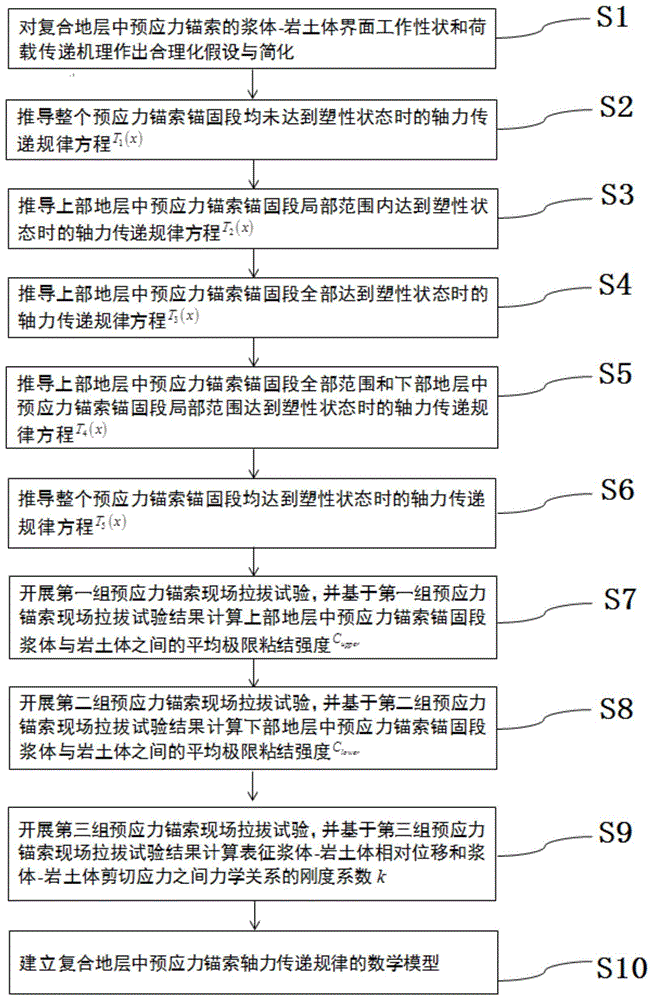
图1为基于现场拉拔试验的复合地层中预应力锚索轴力传递规律数学模型的构建方法的流程图。

图2为整个预应力锚索锚固段均未达到塑性状态时的复合地层中预应力锚索示意图。

图3为上部地层中预应力锚索锚固段局部范围内达到塑性状态时的复合地层中预应力锚索示意图。

图4为上部地层中预应力锚索锚固段全部达到塑性状态时的复合地层中预应力锚索示意图。

图5为上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的复合地层中预应力锚索示意图。

图6为整个预应力锚索锚固段均达到塑性状态时的复合地层中预应力锚索示意图。

图7为第一组预应力锚索现场拉拔试验示意图。

图8为第二组预应力锚索现场拉拔试验示意图。

图9为第三组预应力锚索现场拉拔试验示意图。

图10为实施例中的预应力锚索布置及相关参数示意图；

具体实施方式

以下结合附图对本发明的具体实施方式做详细描述，应当指出的是，实施例只是对发明的具体阐述，不应视为对发明的限定，实施例的目的是为了让本领域技术人员更好地理解和再现本发明的技术方案，本发明的保护范围仍应当以权利要求书所限定的范围为准。

如图1所示，本发明提供一种基于现场拉拔试验的复合地层中预应力锚索轴力传递规律数学模型的构建方法，所述构建方法的步骤为：

(1)对复合地层中预应力锚索的浆体-岩土体界面工作性状和荷载传递机理作出合理化假设与简化；

所述假设与简化的内容具体为：

(1.1)随拉拔力的不断增大，复合地层中预应力锚索的浆体-岩土体界面工作性状逐渐由弹性状态向塑性状态过渡，

如图2所示，当拉拔力满足公式(1c)时，整个预应力锚索锚固段均未达到塑性状态(即整个锚固段均处于弹性状态)，此时处于塑性状态的锚固段长度满足

如图3所示，当拉拔力满足公式(2c)时，上部地层中预应力锚索锚固段局部范围内达到塑性状态，此时处于塑性状态的预应力锚索锚固段长度满足

如图4所示，当拉拔力满足公式(3c)时，上部地层中预应力锚索锚固段全部达到塑性状态，此时处于塑性状态的预应力锚索锚固段长度满足

如图5所示，当拉拔力满足公式(4c)时，上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态，此时处于塑性状态的锚固段长度满足

如图6所示，当拉拔力满足公式(5c)时，整个预应力锚索锚固段均达到塑性状态，此时处于塑性状态的预应力锚索锚固段长度满足

(1.2)当复合地层中预应力锚索的浆体-岩土体界面工作性状处于弹性阶段时，复合地层中预应力锚索的浆体-岩土体相对位移和复合地层中预应力锚索的浆体-岩土体剪切应力之间的力学关系符合虎克定律；

(1.3)当复合地层中预应力锚索的浆体-岩土体界面工作性状处于塑性阶段时，复合地层中预应力锚索的浆体-岩土体剪切应力随复合地层中预应力锚索的浆体-岩土体相对位移的增大保持不变；

(1.4)复合地层中预应力锚索的荷载传递机理符合弹簧-粘片力学模型。

(2)推导整个预应力锚索锚固段均未达到塑性状态时的轴力传递规律方程t1(x)，推导过程为：

整个预应力锚索锚固段均未达到塑性状态时的浆体-岩土体剪切应力分布函数f1(x)表达式为：

对公式(1a)在0→x范围内进行积分，得到整个预应力锚索锚固段均未达到塑性状态时的轴力传递规律方程t1(x)为：

其中，p1^pullout是整个预应力锚索锚固段均未达到塑性状态时预应力锚索受到的拉拔力，范围为

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

是预应力锚索锚固段总长度；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

(3)推导上部地层中预应力锚索锚固段局部范围内达到塑性状态时的轴力传递规律方程t2(x)，推导过程为：

假设从自预应力锚索锚固段始端算起，此时处于塑性状态的预应力锚索锚固段长度为满足的条件为：

上部地层中预应力锚索锚固段局部范围内达到塑性状态时的浆体-岩土体剪切应力分布函数f2(x)为：

对公式(2a)在0→x范围内进行积分，得到上部地层中预应力锚索锚固段范围内达到塑性状态时的轴力传递规律方程t2(x)为：

其中，是上部地层中预应力锚索锚固段局部范围内达到塑性状态时预应力锚索受到的拉拔力，范围为：

是上部地层中的预应力锚索锚固段长度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

与之间的关系为

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

(4)推导上部地层中预应力锚索锚固段全部达到塑性状态时的轴力传递规律方程t3(x)，推导过程为：

此时处于塑性状态的预应力锚索锚固段长度＝上部地层中的预应力锚索锚固段长度

上部地层中锚固段全部达到塑性状态时的浆体-岩土体剪切应力分布函数f3(x)为：

将公式(3a)在0→x范围内进行积分，得到上部地层中锚固段全部达到塑性状态时的轴力传递规律方程t3(x)为：

其中，是上部地层中预应力锚索锚固段全部达到塑性状态时预应力锚索受到的拉拔力，范围为：

clower是下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

(5)推导上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的轴力传递规律方程t4(x)，推导过程为：

此时处于塑性状态的预应力锚索锚固段长度满足的条件为：

上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的浆体-岩土体剪切应力分布函数f4(x)为：

将公式(4a)在0→x范围内进行积分，得到上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的轴力传递规律方程t4(x)为：

其中，是上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时预应力锚索受到的拉拔力，范围为：

clower是下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

k是表征浆体-岩土体相对位移和表征浆体-岩土体剪切应力之间力学关系的刚度系数；

e是预应力锚索钢绞线的弹性模量；

a是预应力锚索钢绞线的横截面面积；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

(6)推导整个预应力锚索锚固段均达到塑性状态时的轴力传递规律方程t5(x)，推导过程为：

此时处于塑性状态的预应力锚索锚固段长度＝预应力锚索锚固段总长度

整个预应力锚索锚固段均达到塑性状态时的浆体-岩土体剪切应力分布函数f5(x)为：

将公式(5a)在0→x范围内进行积分，得到整个预应力锚索锚固段均达到塑性状态时的轴力传递规律方程t5(x)：

其中，是整个锚固段均达到塑性状态时预应力锚索受到的拉拔力，

clower是下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度；

是下部地层中的预应力锚索锚固段长度；

是预应力锚索锚固段总长度；

π是圆周率；

x是预应力锚索锚固段上某点至预应力锚索锚固段末端的距离；

dgr是预应力锚索锚固段浆体的直径；

cupper是上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度。

(7)开展第一组预应力锚索现场拉拔试验，并基于第一组预应力锚索现场拉拔试验结果，计算上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度cupper，计算过程为：

如图7所示，在第一组预应力锚索现场拉拔试验中，钻孔仅钻至上部地层中，预应力锚索锚锚固段仅位于上部地层中；第一组预应力锚索现场拉拔试验应加载至拉出破坏；上部地层中预应力锚索锚锚固段浆体与岩土体之间的平均极限粘结强度cupper计算式为：

其中，π是圆周率；

是第一组预应力锚索现场拉拔试验达到拉出破坏时的极限拉拔力；

dgr1是第一组预应力锚索现场拉拔试验的锚固段钻孔半径；

是第一组预应力锚索现场拉拔试验的锚固段长度。

(8)开展第二组预应力锚索现场拉拔试验，并基于第二组预应力锚索现场拉拔试验结果，计算下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度clower，计算过程为：

如图8所示，在第二组预应力锚索现场拉拔试验中，钻孔钻至下部地层中，预应力锚索锚固段仅位于下部地层中；第二组预应力锚索现场拉拔试验应加载至拉出破坏；下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度计算式为；

其中：π是圆周率；

是第二组预应力锚索现场拉拔试验达到拉出破坏时的极限拉拔力；

dgr2为第二组预应力锚索现场拉拔试验的锚固段钻孔半径；

为第二组预应力锚索现场拉拔试验的锚固段长度。

(9)开展第三组预应力锚索现场拉拔试验，并基于第三组预应力锚索现场拉拔试验结果，计算表征浆体-岩土体相对位移和浆体-岩土体剪切应力之间力学关系的刚度系数k，计算过程为：

如图9所示，在第三组预应力锚索现场拉拔试验中，钻孔钻至下部地层中，预应力锚索锚固段位于上部地层和下部地层中；第三组预应力锚索现场拉拔试验不需要加载至拉出破坏，但应至少加载至上部地层中预应力锚索锚固段局部范围内开始达到塑性状态；表征浆体-岩土体相对位移和浆体-岩土体剪切应力之间力学关系的刚度系数k计算式为：

其中：π是圆周率；

dgr3是第三组预应力锚索现场拉拔试验的锚固段钻孔半径；

etest3是第三组预应力锚索现场拉拔试验中预应力锚索钢绞线的弹性模量；

atest3是第三组预应力锚索现场拉拔试验中预应力锚索钢绞线的横截面面积；

是第三组预应力锚索现场拉拔试验的锚固段长度；

β是第三组预应力锚索现场拉拔试验获得的荷载-位移曲线的弹性阶段的斜率；

是第三组预应力锚索现场拉拔试验的自由段长度。

(10)建立复合地层中预应力锚索轴力传递规律的数学模型；

将所获取的相关参数代入t1(x)、t2(x)、t3(x)、t4(x)、t5(x)中，即建立起复合地层中预应力锚索轴力传递规律的数学模型。

具体实施例：

该具体应用案例为襄阳市东西轴线道路工程鱼梁洲段某基坑工程，基坑围护结构形式为锚拉地连墙和格型地连墙组合方式。

如图10所示，该实施例中的预应力锚索锚固段穿越细砂层和卵石层两种地层，细砂层为上部地层(厚度为7m)，卵石层为下部地层(厚度为10m)，预应力锚索采用4×φ15.2-7低松弛钢绞线，钻孔水平倾角为25°，预应力锚固段浆体的直径dgr＝0.133m，预应力锚索锚固段总长度预应力锚索现场拉拔试验的自由段长度上部地层中的预应力锚固段长度下部地层中的预应力锚固段长度预应力锚索钢绞线的弹性模量e＝1.95gpa，预应力锚索钢绞线的横截面面积a＝5.6×10^-4m²。

试验仪器采用电动油泵+液压穿心式千斤顶系统加载，钢绞线伸长量采用钢直尺测量，型钢位移采用全站仪测量。

s1，对复合地层中预应力锚索的浆体-岩土体界面工作性状和荷载传递机理作出合理化假设与简化；

s2，推导整个预应力锚索锚固段均未达到塑性状态时的轴力传递规律方程t1(x)；

s3，推导上部地层中预应力锚索锚固段局部范围内达到塑性状态时的轴力传递规律方程t2(x)；

s4，推导上部地层中预应力锚索锚固段全部达到塑性状态时的轴力传递规律方程t3(x)；

s5，推导上部地层中预应力锚索锚固段全部范围和下部地层中预应力锚索锚固段局部范围达到塑性状态时的轴力传递规律方程t4(x)；

s6，推导整个预应力锚索锚固段均达到塑性状态时的轴力传递规律方程t5(x)；

s7，开展第一组预应力锚索现场拉拔试验，计算上部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度cupper＝30kpa；

s8，开展第二组预应力锚索现场拉拔试验，计算下部地层中预应力锚索锚固段浆体与岩土体之间的平均极限粘结强度clower＝200kpa；

s9，开展第三组预应力锚索现场拉拔试验，计算表征浆体-岩土体相对位移和浆体-岩土体剪切应力之间力学关系的刚度系数k＝176.672kn/m；

s10，将基于预应力锚索现场拉拔试验所获取的cupper、clower、k等相关参数代入t1(x)、t2(x)、t3(x)、t4(x)、t5(x)中，即建立起复合地层中预应力锚索轴力传递规律的数学模型，数学模型为：

尽管已描述了本申请的优选实施例，但本领域内的技术人员一旦得知了基本创造性概念，则可对这些实施例作出另外的变更和修改。所以，所附权利要求意欲解释为包括优选实施例以及落入本申请范围的所有变更和修改。