一种基于Bezier样条的机器人实时拐角过渡方法与流程

本发明属于工业机器人轨迹规划领域，更具体地，涉及一种基于Bezier样条的机器人实时拐角过渡方法。
背景技术：
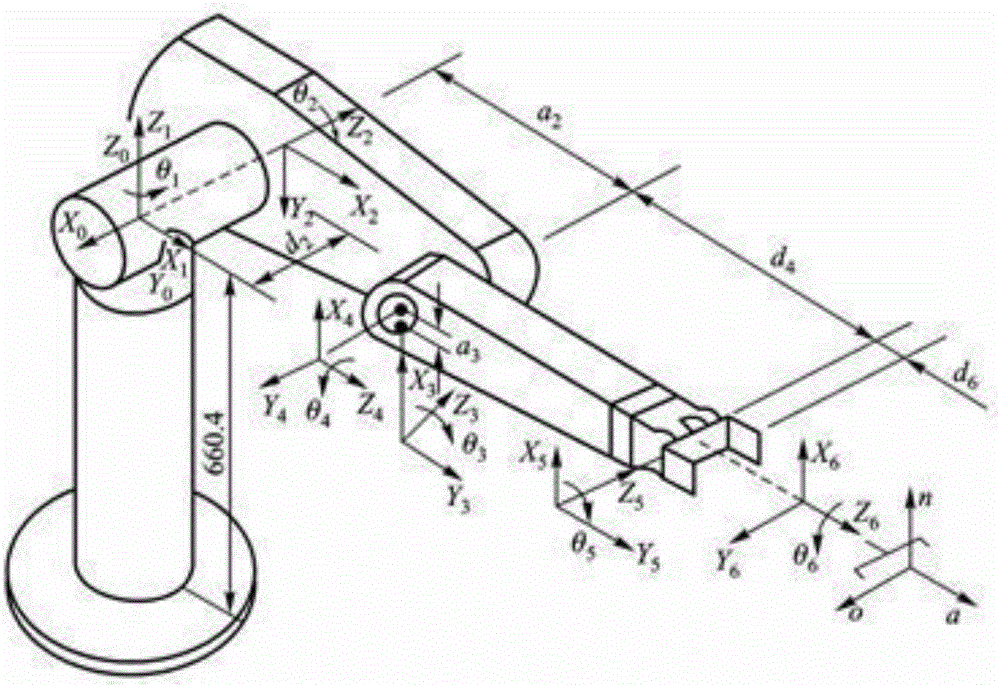
：工业机器人的轨迹规划方式根据是否通过指定路径点主要分为两种方式。通过指定路径点的轨迹规划由操作人员指定一系列路径点，机器人按给定的运动指令通过每一个路径点，并且在每一个路径点附近区域完成减速，停止再加速的过程，该方法可以实现精确到达指令要求的位置，但是在经过路径点时会有停顿，因此当路径点较多时会耗费较多时间，降低了整体效率。不通过指定路径点的轨迹规划即拐角过渡，由操作人员指定过渡路径点以及过渡半径，机器人按照过渡半径计算过渡段，其在过渡区域内采用曲线过渡，位置连续，且过渡曲线不经过过渡路径点，因此不需要降速为0，从而整体提高了作业效率。根据规划过渡曲线的空间不同，拐角过渡方法又可以分为关节空间下的拐角过渡和笛卡尔空间的拐角过渡。如果拐角前后均为PTP(点到点)运动指令，则表示机器人在关节空间进行轨迹规划，此时的拐角过渡可以根据关节空间下的过渡半径约束来进行关节空间过渡曲线的规划。如果拐角前后均为线性运动指令，则表示机器人在笛卡尔空间进行轨迹规划，此时的拐角过渡可以根据笛卡尔空间下的过渡半径约束进行笛卡尔空间过渡曲线的规划。如果拐角前后分别为PTP(点到点)和线性运动指令，则规划过渡曲线的空间与前后运动指令所对应的轨迹规划空间不相同。因此存在着无法满足不同空间的过渡半径约束的问题。对于相同运动指令之间的过渡曲线的最大误差可以通过控制过渡曲线的参数实现，但是不同运动指令的过渡曲线的最大误差约束却不能用相同的方法进行计算求解。目前只能根据生成的过渡曲线计算距离过渡路径点的最大误差，而不能采用最大误差计算过渡曲线参数从而控制过渡曲线的生成。因为这些问题，目前已有的工业机器人PTP(点到点)和线性运动指令之间的拐角过渡不能实现过渡半径和最大误差的同时约束，增大了拐角过渡的误差。技术实现要素：针对现有技术的以上缺陷和改进需求，本发明提供了一种基于Bezier样条曲线的机器人实时拐角过渡方法，其目的在于提供了一种能在PTP(点到点)运动指令和线性运动指令之间进行拐角过渡轨迹规划方法。由此解决了现有工业机器人在PTP(点到点)运动指令和线性运动运动指令之间过渡时无法满足过渡半径和最大过渡误差同时约束的技术问题。为实现上述目的，按照本发明，提供了一种基于Bezier样条的机器人实时拐角过渡方法，其特征在于，该方法包括下列步骤：(a)记录关节空间起始点的坐标qstart及其运动速度大小关节空间过渡点的坐标qvia，笛卡尔空间目标点的坐标Pend，笛卡尔空间的过渡半径R以及最大误差约束ε。笛卡尔空间过渡点的坐标为Pvia，将所述Pvia用所述qvia表示；(b)通过笛卡尔空间过渡曲线起点的坐标满足的所述过渡半径R的约束条件，计算出所述笛卡尔空间过渡曲线起点的坐标P0，并通过弦截法计算出关节空间过渡曲线起点的坐标q0；(c)通过所述Pvia、所述Pend和所述笛卡尔空间的过渡半径R的约束条件，计算出笛卡尔空间过渡终点的坐标P1；(d)关节空间匀速运动，所述关节空间起始点的运动速度的速度方向等于所述关节空间过渡曲线起点的速度方向，采用雅克比矩阵转换将所述关节空间过渡曲线段起点的速度大小映射到所述笛卡尔空间过渡曲线起点速度，计算该速度方向的单位矢量V0，利用所述笛卡尔空间目标点的坐标Pend和所述笛卡尔空间过渡点的坐标Pvia，计算所述笛卡尔空间过渡曲线终点速度方向的单位矢量V1；(e)预设笛卡尔空间过渡曲线中间控制点的坐标P2和P3与所述V0和所述V1的关系式(一)，结合所述最大误差约束的条件ε，求解出所述P2和所述P3，同时计算出三次Bezier样条曲线的构造函数；(f)采用S型加减速对前后段以及过渡曲线进行速度规划以及插补。作为进一步优选地，在步骤(a)中，所述用qvia表示Pvia优选采用运动学正解方程，其关系式(二)如下，其中，qvia＝[θ1θ2θ3θ4θ5θ6]，θ1，θ2，θ3，θ4，θ5和θ6分别代表旋转关节1～6的关节变量，c1＝cosθ1、s1＝sinθ1、c23＝cos(θ2+θ3)、s23＝sin(θ2+θ3)，其余依此类推，a2是连杆2的连杆长度参数，a3是连杆3的连杆长度参数，d3是连杆1和连杆2之间的连杆偏置参数，d4是连杆3和连杆4之间的连杆偏置参数，Pvia=c1(a2c2+a3c23-d4s23)-d2s1s1(a2c2+a3c23-d4s23)-d2c1-a3s23-a2s2-d4c23.]]>作为进一步优选地，在步骤(b)中，所述过渡半径的约束条件优选采用以下关系式(三)：|P0-Pvia|-R＝0。作为进一步优选地，在步骤(c)中，所述过渡终点的笛卡尔坐标P1优选采用以下关系式(四)：P1=Pvia-Pvia-Pend|Pvia-Pend|R.]]>作为进一步优选地，在步骤(d)中，所述雅克比矩阵优选采用以下表达式(五)，J(q)＝[J1(q)J2(q)J3(q)J4(q)J5(q)J6(q)]J1(q)=-s1(a1+a2c2+a3c23+d4s23)c1(a1+a2c2+a3c23+d4s23)0001]]>J2(q)=c1(d4c23-a3s23-a2s2)s1(d4c23-a3s23-a2s2))d4s23+a3c23+a2c2s1-c10]]>J3(q)=-c1(a3s23-d4c23)-s1(a3s23-d4c23)a3c23+d4s23s1-c10]]>J4(q)=000c1s23s1s23-c23]]>J5(q)=000s1c4-c1s4c23-c1c4-s1s4c23-s4s23]]>J6(q)=000c1c5s23+s5(s1s4+c1c4c23)c1s5s23+s5(-c1s4+s1c4c23)-c5c23+c4s5s23;]]>所述V0优选采用以下表达式(六)：V0=J(q0)q0.|J(q0)q0.|;]]>所述V1优选采用以下表达式(七)：V1=Pvia-Pend|Pvia-Pend|.]]>作为进一步优选地，在步骤(e)中，所述关系式(一)优选采用以下表达式：P2-P0=λ3V0P1-P3=λ3V1;]]>所述三次Bezier样条曲线的构造函数优选采用以下表达式(八)，其中t是0～1之间的任意数：S(t)＝(1-t)3P0+3t(1-t)2P2+3t2(1-t)P3+t3P1；所述最大误差约束的条件优选采用以下表达式(九)，并由所述表达式(九)获得一元二次方程，其中S(t0)中t0取0～1之间的任意数：|S(t0)-Pvia|＝ε；通过所述一元二次方程计算出λ优选采用以下表达式(十)，且λ取最小正数值λ=2(M1·M2)±Δ2M1;]]>其中Δ＝(2(M1·M2))2-4|M1|2||M2|2-ε2|M1=V0|V0|t0(1-t0)2-V1|V1|t02(1-t0)M1∈R3M2=(P0(1-t0)3+P1t03+3P0t0(1-t0)2+3P1t02(1-t0))-PviaM2∈R3]]>总体而言，通过本发明所构思的以上技术方案与现有技术相比，能够取得下列有益效果：1、本发明通过采用拐角过渡的方法，在指定的过渡区域内采用曲线过渡实现位置连续，在笛卡尔空间和关节空间，过渡曲线起点的速度都不为0，避免了经过指定路径点时的停顿，解决了当路径点较多时会耗费时间长的问题，整体提高了作业效率；2、本发明通过采用笛卡尔空间过渡曲线起点满足过渡半径的约束条件，算出了笛卡尔空间过渡曲线起点的坐标P0，并通过弦截法算出关节空间过渡曲线起点的坐标q0，实现了不同空间的过渡半径约束条件；3、本发明通过采用雅克比矩阵转换将所述关节空间过渡曲线段起点的速度大小映射到所述笛卡尔空间过渡曲线起点速度方向的单位矢量V0，然后利用最大误差约束的条件求解Bezier样条曲线的构造函数，实现了不同运动指令(笛卡尔空间和关节空间指令)之间的最大误差约束的条件，同时实现了过渡半径和最大误差的同时约束，减少了拐角过渡的误差；4、本发明通过采用了运动学正解方程、弦截法、雅克比矩阵和一元二次方程求解等方法实现了关节空间到笛卡尔空间的拐角过渡，整体方案简单，高质量地完成了整个拐角过渡过程，并且整个过程便于操作和控制。附图说明图1是机器人点到点运动指令和线性运动指令之间拐角过渡方法的流程图；图2是按照本发明的优选实施例所构建的机器人结构图；图3是按照本发明的优选实施例所构建的进行速度规划和插补后的拐角过渡效果图。具体实施方式为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。图1是机器人点到点运动指令和线性运动指令之间拐角过渡方法的流程图，如图1所示，该拐角过渡方法具体包括以下步骤：S1：记录PTP(点到点)运动指令起始点的关节坐标qstart，线性运动指令目标点的笛卡尔空间坐标值Pend，给定笛卡尔空间的过渡半径R以及最大误差约束ε。路径过渡点的关节空间坐标为qvia，笛卡尔空间坐标Pvia。由运动学正解方程可以将qvia表示为Pvia，图2是按照本发明的优选实施例所构建的机器人结构图，本实例中采用基于图2所示的PUMA机器人结构，相应的运动学正解方程如下：Pvia=c1(a2c2+a3c23-d4s23)-d2s1s1(a2c2+a3c23-d4s23)-d2c1-a3s23-a2s2-d4c23]]>式中，c1＝cosθ1、s1＝sinθ1、c23＝cos(θ2+θ3)、s23＝sin(θ2+θ3)，其余依此类推。qvia＝[θ1θ2θ3θ4θ5θ6]。a2、a3、d2、d4分别为机器人连杆参数。S2：计算PTP(点到点)运动指令下的过渡曲线段起点P0。由于约束在笛卡尔空间进行描述，过渡曲线段起点的笛卡尔空间坐标需满足如下约束条件：|P0-Pvia|-R＝0由于PTP(点到点)运动指令下机器人在关节空间进行轨迹规划，所以需要利用机器人运动学正解将关节空间的坐标值映射到笛卡尔空间。PTP(点到点)运动指令下机器人运动轨迹在映射到笛卡尔空间后为不规则曲线，因此不能找到距离约束的解析解。采用弦截法可以计算出任意精度的数值解。从而得出过渡曲线段起点的关节空间坐标和笛卡尔空间坐标。S3：在线性运动指令下的过渡终点P1可以根据给定的路径过渡点Pvia和线性运动指令的目标点Pend以及过渡半径R求出：P1=Pvia-Pvia-Pend|Pvia-Pend|R]]>S4：V0、V1分别为过渡曲线段起点和过渡曲线段终点的笛卡尔空间速度方向的单位矢量，在计算V0时需要将关节空间运动到该点时的关节速度映射到笛卡尔空间，采用雅克比矩阵进行转换：V0=J(q0)q0.|J(q0)q0.|]]>V1=Pvia-Pend|Pvia-Pend|]]>其中q0，J(q0)分别为过渡起点的关节坐标，关节速度和该工业机器人的雅克比矩阵转换式。对于实例中所用机器人，其雅克比矩阵为：J(q)＝[J1(q)J2(q)J3(q)J4(q)J5(q)J6(q)]J1(q)=-s1(a1+a2c2+a3c23+d4s23)c1(a1+a2c2+a3c23+d4s23)0001]]>J2(q)=c1(d4c23-a3s23-a2s2)s1(d4c23-a3s23-a2s2))d4s23+a3c23+a2c2s1-c10]]>J3(q)=-c1(a3s23-d4c23)-s1(a3s23-d4c23)a3c23+d4s23s1-c10]]>J4(q)=000c1s23s1s23-c23]]>J5(q)=000s1c4-c1s4c23-c1c4-s1s4c23-s4s23]]>J6(q)=000c1c5s23+s5(s1s4+c1c4c23)c1s5s23+s5(-c1s4+s1c4c23)-c5c23+c4s5s23]]>S5：计算Bezier过渡曲线参数方程。P2、P3为样条曲线的中间控制点坐标。规定过渡曲线起点与终点的速度方向分别与按照原始指令进行运动规划时经过该点时的速度方向V0、V1相同。假设存在如下关系：P2-P0=λ3V0]]>P1-P3=λ3V1]]>λ为比例系数。三次Bezier样条曲线的构造函数为S(t)＝(1-t)3P0+3t(1-t)2P2+3t2(1-t)P3+t3P1t∈[0,1]其中，t为样条曲线的控制参数。P0、P1分别为样条曲线的首末控制点坐标。根据约束条件，设置当t为定值t0，且t0＝0.5时，过渡曲线段与路径过渡点之间的距离为ε，则有：|S(t0)-Pvia|＝ε由此可列出一元二次方程求解λ。先对方程判别式进行分析，防止出现无解情况。Δ＝(2(M1·M2))2-4|M1|2||M2|2-ε2|其中，M1,M2均为三维实数向量，M1=V0|V0|t0(1-t0)2-V1|V1|t02(1-t0)M1∈R3M2=(P0(1-t0)3+P1t03+3P0t0(1-t0)2+3P1t02(1-t0))-PviaM2∈R3]]>当Δ<0说明当t＝t0时无法找到满足误差公式的解。因此需要替换不同的参数值直到Δ≥0，此时通过下式计算λ：λ=2(M1·M2)±Δ2M1]]>由于一元二次方程存在两个解，需取较小的正数值作为最终解，保证速度不反向以及过渡曲线位于原轨迹路径的内侧。根据上述公式可以求解出P2、P3，从而表达出Bezier过渡曲线的参数方程。S6：采用S型加减速对前后段以及过渡曲线进行速度规划以及插补。本发明的一个优选实施例如下：设PTP(点到点)运动指令起始点的关节空间坐标为qstart＝[8.0482.3-16.7496.68.04]，单位为度。线性运动指令目标点的位置坐标为Pend＝[920130300]，单位为毫米。过渡路径点的关节空间坐标为qvia＝[7.9882.1-17494.87.26]，经过运动学正解计算得出其笛卡尔空间位置坐标为Pvia＝[7900300]。过渡半径为150mm，最大误差为60mm。根据以上约束，计算得出PTP(点到点)运动指令下的过渡曲线段起点的笛卡尔空间坐标为P0＝[939.317.1298.9]，线性运动指令下的过渡曲线段终点的笛卡尔坐标为P1＝[896.3106.3300]。比例系数λ＝451。P2＝[814.28.1216]，P3＝[80398300]。获得过渡段参数曲线后，进行速度规划和插补，图3是按照本发明的优选实施例所构建的进行速度规划和插补后的拐角过渡效果图，如图3所示的原始轨迹和插补后的过渡曲线，可以看出用Bezier过渡曲线代替原始的轨迹可以实现圆滑的拐角过渡。本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3