一种多自由度机器人的类脑学习控制方法与流程

本发明涉及机器人控制领域和不确定非线性动态系统控制领域，特别涉及一种多自由度机器人的仿生智力控制方法。
背景技术：
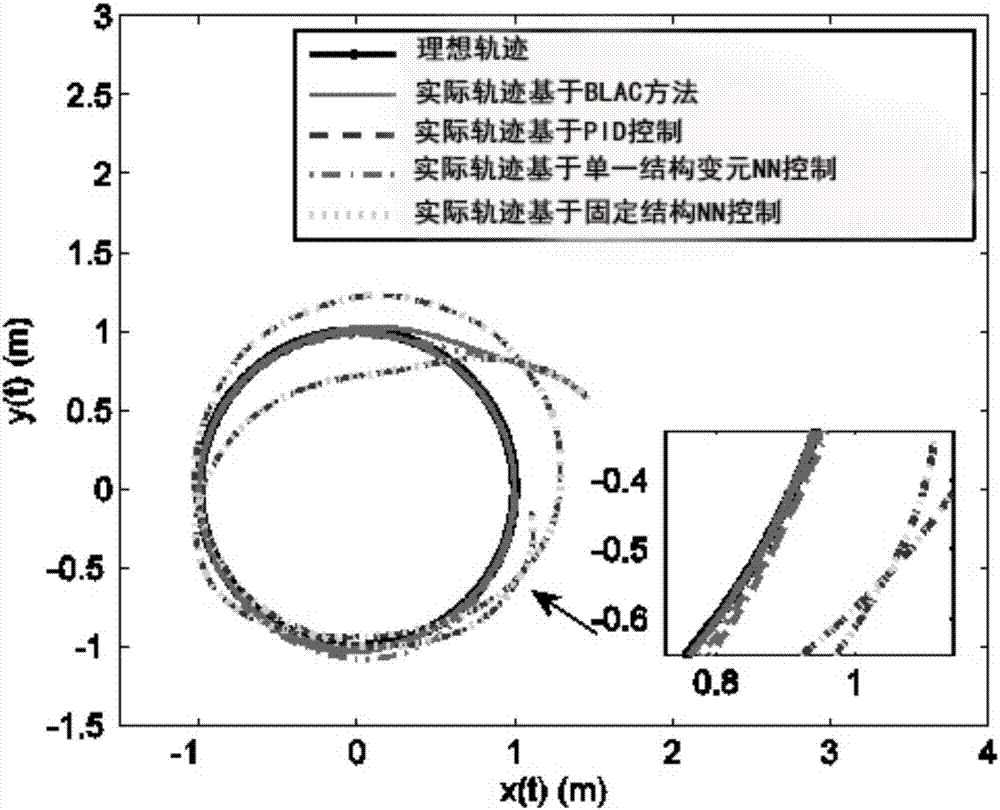
：多关节机械臂是mimo系统控制的典型对象。与自适应nn稳定性分析技术结合，目前机械臂控制取得了很多成果，比如：为了提升轨迹跟踪控制的精度和综合性能，一些学者针对末端执行器的位置跟踪任务，设计了无需有效载荷质量先验信息的在线nn自适应控制器；一些学者通过nn控制实现了机器人与不确定粘性环境的交互；一些学者结合小脑模型关节控制(cmac)和回声状态网络，针对非光滑的非线性动力学系统提出了一种输出跟踪误差受限的鲁棒位置控制方法。由于这些控制策略中采用的是固定结构的nn模型，因此在实际使用场景中存在如下问题：nn控制以万能逼近定理(uat)为严格前提，在控制器设计和集成阶段需要确保nn能够安全有效地发挥学习/近似能力，一旦nn参数设置不恰当，不仅会使nn整体逼近能力丧失，还会影响系统的平稳安全运行。其主要问题在于缺少系统化、通用性强的参数选取方法，包括神经元个数，基函数及其结构参数(如，高斯基函数的中心和宽度参数)等。在绝大多数nn控制方法中，这些参数往往需要人工选定，而不能根据系统的实际输出进行自动调整，使得系统控制性能对这些参数格外敏感。比如，设置过多的神经元会造成参数过拟合并且加重运算负担，设置过少则会达不到学习的效果；再比如，rbf-nn设计中，若高斯基函数中心与宽度的设计不在nn输入有效的映射范围内，则会导致rbf-nn失效。虽然通过梯度下降法能够得到在线调节的参数，但却存在局部最优解的情况，并且很难从理论上证明系统的全局一致最终收敛。为巩固nn性能并确保功能的有效性，研究人员作出了各种尝试，比如切换控制方法，自组织控制方法，以及基于受限李雅普诺夫函数的方法。总体来说，传统nn控制的设计与分析过程十分复杂，所建立的控制器通常结构复杂，而且需要占用大量的系统在线运算资源。技术实现要素：有鉴于此，本发明的目的是提供一种多自由度机器人的类脑学习控制方法，类脑学习控制方法：brainlearningassociatedcontrol，blac，其针对具有跳变扰动和未知不确定性的多自由度机器人系统，以解决在关节空间(方阵情形)与笛卡尔空间(非方阵情形)中多自由度机器人系统输出的轨迹跟踪问题，旨在避免线性化处理过程和繁琐的设计流程，改善系统的自学习和自适应能力。本发明多自由度机器人的类脑学习控制方法，包括以下步骤：多自由度机器人的类脑学习控制方法，其特征在于：包括以下步骤：步骤一、建立多自由度机器人系统动力学模型；对于含有n个旋转关节的刚性电驱动机械臂，其动力学方程为：其中，q＝[q1,...,qn]t∈rn，分别表示关节角位移，关节角速度和关节角加速度向量；d(q)∈rn×n为对称正定惯性矩阵，为向心力与科氏力矩，g(q)∈rn和分别为重力与摩擦力，δ(t)∈rn表示外部扰动和建模不确定性；u∈rl为系统控制输入信号，表示关节电机产生的实际力矩与控制信号间的非线性映射；记机械臂末端执行器的位姿为p＝[p1,...,pm]t∈rm，m表示末端执行器在笛卡尔任务空间的自由度，且满足m≤n以涵盖冗余运动情形；并引入如下多入多出非仿射系统：其中，系统状态向量x＝[x1,...,xn]t∈rn；控制输入向量u＝[u1,...,ul]t∈rl；系统输出y＝[y1,...,yn]t∈rn；f(·)＝[f1(·),...,fn(·)]t∈rn和fd(x,t)＝[fd1,...,fdn]t∈rn分别表示未知光滑非线性函数向量和不确定外界扰动或子系统故障引起的额外跳变；根据中值定理可知存在k＝1,...,n，j＝1,...,l，使得非仿射函数fk(·)满足且定义跟踪误差e(t)＝y-yd＝[e1,...,en]t，取β>0为一已知常数，定义滤波误差向量：其关于时间的导数为：其中，集总不确定性项l(·)表示为l(·)＝f(x,0)±fd(x,t)+yd且虚拟控制增益矩阵中间变量当b(·)为未知且非必须对称型方阵时，控制器唯一可用信息是(b+bt)/2为正定或负定，正定(b+bt)/2的最小特征值恒正，故存在某未知正常数ω使得当b(·)为部分已知的非方矩阵时，将其解耦表示为b(x,u)＝a(x)m(x,u)，其中a(·)∈rn×l为已知有界的行满秩矩阵，m(·)∈rl×l为完全未知且非必须对称型方阵；已知a(m+mt)at/2为对称且正定，故存在某未知正常数ν使得步骤二、构建基于msae-nn的智能控制器u：1)采用多内涵自调节型神经网络msae-nn对l(·)的l2范数上界进行重构，即其中为输入信号，分别为第i个子网络的第j个神经元新增神经元和将被剔除神经元的基函数，是时变理想权值；且有重构误差|ε(z)|<εc<∞；又因为和ε(z)有界，故存在未知常量wε使得||wε(z,t)||≤wε；2)设计机器人系统在关节空间空间的控制器u：给定理想关节角度轨迹qd(t)∈rn，则关节角位移跟踪误差向量表示为：ej＝q-qd∈rn滤波误差sj(t)及其动特性设计神经自适应控制器u如下其中控制参数k0>0，θ>0，β1>||sj(0)||，γ0>0，γ1>02)设计机器人系统在笛卡尔任务空间的控制器u给定末端执行器理想位姿pd(t)∈rm，则其位姿跟踪误差向量表示为：ec＝p-pd∈rm滤波误差sc(t)及其动特性为：显然，当m<l时，b(·)为非方矩阵。结合情形2，b(·)可被分解为两矩阵相乘形式，即b(·)＝am，并且符合行满秩矩阵a＝j(q)∈rm×l，正定对称方阵设计神经神经自适应控制器u如下其中控制参数k0>0，θ＞0,β1>||sc(0)||，γ0>0，γ1>0；步骤三、将控制器u作用到步骤一)建立的机器人系统，使输出y(t)按给定精度β0跟踪期望轨迹xd(t)，同时确保系统跟踪误差e(t)在t≥0有界。本发明的有益效果：本发明多自由度机器人的类脑学习控制方法，其解决了在关节空间(方阵情形)与笛卡尔空间(非方阵情形)中多自由度机器人系统输出的轨迹跟踪问题。与绝大多数机器人神经网络控制方法不同的是，类脑学习控制方法完整地继承了msae-nn的优质特性，网络具有结构多元化的基函数以及时变的理想权值，并且能够根据系统当前的输出偏差对神经元个数进行实时调整。这一方面避免了人工通过反复试验的方式来配置nn相关参数的繁冗过程；另一方面，有助于巩固与强化系统的自学习和自适应能力，提升其整体智能程度。值得一提的是，由于控制算法本身并不依赖机器人动力学模型的精确信息，并且也无需计算传统nn中庞大规模的权值估计向量，而是通过引入虚拟参数的方式巧妙地将矩阵运算转化为标量运算，因此所设计的控制器具有结构简单的特点，即使对于存在高度不确定非线性的系统，也能以较低的成本在工程系统中集成。附图说明图1为含有3个旋转关节的三连杆平面机械臂的结构示意图。图2为使用四种控制策略得到的末端执行器的轨迹跟踪情况示意图。图3为在四种控制方法作用下末端执行器的位置跟踪误差演变情况示意图。图4为描绘blac、对照组2和3的权值/虚拟参数变化情况的示意图。图5为blac方法和对照组2的神经元实时调节结果示意图。图6和图7分别为四种控制策略产生的关节控制信号及相应关节角度输出结果的示意图。具体实施方式下面结合附图和实施例对本发明作进一步描述。本实施例多自由度机器人的类脑学习控制方法，包括以下步骤：步骤一、建立多自由度机器人系统动力学模型；对于含有n个旋转关节的刚性电驱动机械臂，其动力学方程为：其中，q＝[q1,...,qn]t∈rn，分别表示关节角位移，关节角速度和关节角加速度向量；d(q)∈rn×n为对称正定惯性矩阵，为向心力与科氏力矩，g(q)∈rn和分别为重力与摩擦力，δ(t)∈rn表示外部扰动和建模不确定性；u∈rl为系统控制输入信号，表示关节电机产生的实际力矩与控制信号间的非线性映射。记机械臂末端执行器的位姿为p＝[p1,...,pm]t∈rm，m表示末端执行器在笛卡尔任务空间的自由度，且满足m≤n以涵盖冗余运动情形。并引入如下多入多出非仿射系统：其中，系统状态向量x＝[x1,...,xn]t∈rn；控制输入向量u＝[u1,...,ul]t∈rl；系统输出y＝[y1,...,yn]t∈rn；f(·)＝[f1(·),...,fn(·)]t∈rn和fd(x,t)＝[fd1,...,fdn]t∈rn分别表示未知光滑非线性函数向量和不确定外界扰动或子系统故障引起的额外跳变。根据中值定理可知存在k＝1,...,n，j＝1,...,l，使得非仿射函数fk(·)满足且定义跟踪误差e(t)＝y-yd＝[e1,...,en]t，取β>0为一已知常数，定义滤波误差向量：其关于时间的导数为：其中，集总不确定性项l(·)表示为l(·)＝f(x,0)±fd(x,t)+yd且虚拟控制增益矩阵中间变量当b(·)为未知且非必须对称型方阵时，控制器唯一可用信息是(b+bt)/2为正定或负定，正定(b+bt)/2的最小特征值恒正，故存在某未知正常数ω使得当b(·)为部分已知的非方矩阵时，将其解耦表示为b(x,u)＝a(x)m(x,u)，其中a(·)∈rn×l为已知有界的行满秩矩阵，m(·)∈rl×l为完全未知且非必须对称型方阵；已知a(m+mt)at/2为对称且正定，故存在某未知正常数ν使得步骤二、构建基于msae-nn的智能控制器u：1)采用多内涵自调节神经网络(msae-nn即：多内涵自调节神经网络)对l(·)的l2范数上界进行重构，即其中为输入信号，φi,j(z)分别为第i个子网络的第j个神经元新增神经元和将被剔除神经元的基函数，是时变理想权值；且有重构误差|ε(z)|<εc<∞；又因为和ε(z)有界，故存在未知常量wε使得||wε(z,t)||≤wε。2)设计机器人系统在关节空间的控制器u：给定理想关节角度轨迹qd(t)∈rn，则关节角位移跟踪误差向量表示为：ej＝q-qd∈rn滤波误差sj(t)及其动特性设计神经自适应控制器u如下其中控制参数k0>0，θ>0，β1>||sj(0)||，γ0>0，γ1>0。2)设计机器人系统在笛卡尔任务空间的控制器u给定末端执行器理想位姿pd(t)∈rm，则其位姿跟踪误差向量表示为：ec＝p-pd∈rm滤波误差sc(t)及其动特性为：显然，当m<l时，b(·)为非方矩阵。结合情形2，b(·)可被分解为两矩阵相乘形式，即b(·)＝am，并且符合行满秩矩阵a＝j(q)∈rm×l，正定对称方阵设计神经自适应控制器u如下其中控制参数k0>0，θ>0，β1>||sc(0)||，γ0>0，γ1>0。步骤三、将控制器u作用到步骤一)建立的机器人系统，使输出y(t)按给定精度β0跟踪期望轨迹xd(t)，同时确保系统跟踪误差e(t)在t≥0有界。下面通过仿真实验，对本实施例中多自由度机器人的类脑学习控制方法的有效性进行验证：以图1所示含有3个旋转关节的三连杆平面机械臂为被控系统，验证blac方法在mimo系统上的有效性，多输入多输出：multiple-inputmultiple-output，mimo。该机械臂系统动力学方程在步骤一中给出，现给出其详细数据：连杆i连杆1连杆2连杆3mi[kg]0.50.50.5li[m]0.30.60.8lci[m]0.150.30.4ii[kg·m2]1.51.00.5给定机器人末端执行器理想位姿为pd＝[xd,yd]t＝[cos(πt),sin(πt)]t，实际位姿p＝[x,y]t，三个关节角度初始值为q(0)＝[q1,q2,q3]t＝[-18°,30°,30°]t，关节角速度初始值为估计虚拟参数初值控制参数k0＝20，权值学习参数γ0＝0.005，γ1＝100，θ＝0.05，hurwitz多项式参数β＝5，受限李函数的界β1＝||1.1×sc(0)||>||sc(0)。msae-nn的配置中，神经元自动增减阈值因子ρ＝0.1和χ＝0.1，网络训练输入采用升余弦函数(raisedcosinebasisfunctions,rcbfs)和高斯函数(gaussianbasisfunctions,gbfs)共同作为神经元的基函数，并且两类基函数对应的神经元初始数量均为5个，即网络中共含10个神经元。系统仿真总时间为4秒，控制周期1毫秒。仿真结果如下：图2给出了使用四种控制策略得到的末端执行器的轨迹跟踪情况。图3展现了四种控制方法作用下末端执行器的位置跟踪误差演变情况。可以清晰看出，在外界扰动和未建模动态存在时，blac方法的精度要高于其他三种方法。值得一提的是，由于blac和对照组2均启用了神经元自动增减策略，其结果要比另外两个对照组效果好。图4描绘了blac、对照组2和3的权值/虚拟参数变化情况。从图中发现，固定结构的nn已失去权值更新能力。因此，在图2中，对照组1和3的轨迹曲线几乎完全重合，进一步印证了固定结构的nn控制在网络参数选取不恰当时，nn存在失效问题。注意到，对照组3的方法并未产生发散结果的原因在于其含有与组1完全相同的反馈控制单元。图5中给出了blac方法和对照组2的神经元实时调节结果。其中，粗线表示采用了gbf和rcbf两种类型的神经元的blac方法，虚线和点划线分别表示rcbf型和gbf型神经元在msae-nn中的各自数量变化情况；黑色粗线为仅采用单一rcbfs的对照组2方法。图6和图7给出了四种控制策略产生的关节控制信号及相应关节角度输出结果。由于在2秒后引入了频率为5hz的扰动信号，控制器会随之产生相应频率的变化，而非产生抖动。有趣的是，在引入扰动后blac方法与对照组2均能使跟踪误差得到收敛，体现了神经元自调节策略对nn自学习能力的强化作用。最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。当前第1页12