偏置腕6R工业机械手笛卡尔轨迹跟踪逆运动学算法

偏置腕6r工业机械手笛卡尔轨迹跟踪逆运动学算法
技术领域
1.本发明涉及一种逆解数值算法，更具体地，涉及偏置腕6r工业机械手笛卡尔轨迹跟踪逆运动学算法。


背景技术：

2.工业机器人逆运动学求解作为机器人离线编程、轨迹规划、控制算法设计等其他课题研究的基础，一直是工业机器人学中的一个经典问题，同样也是研究热点。逆运动学求解的实质是完成机器人工作空间到关节空间的映射，逆运动学方程组具有高维、非线性的特点，求解复杂且不易求出。在工业机器人应用中，最后三个关节相交于一点的6r工业球面腕关节机械手(6riswm)应用最为广泛，因为它具有逆运动学(ik)解析解。近年来，为了使工业机械手的手腕更好地布置管道，并具有更大的水平延伸范围，设计师在6riswm的手腕上增加了一个偏移量，如motoman epx2050和fanuc p-250ib喷涂机器人等，这种结构改进使得机械手的运动学方程更加耦合和复杂，因此没有ik解析解。
3.6r偏置腕工业机器人(6rimwow)的ik(逆运动学)问题是研究工业机器人必须面对和解决的一个问题，将6rimwow的ik转化为一维非线性方程的寻根问题是一个很好的选择。
4.现有逆运动学解法虽然也可以解决大部分工业机器人的逆运动学问题，但是仍然缺乏一种通用方法，既具有几何直观意义推导出逆解公式，数值求解过程中又可以满足实时、高精度控制。


技术实现要素：

5.本发明针对现有技术中逆运动学解法推导过程十分繁琐耗时，无法保证离线求解和实时求解问题，提供偏置腕6r工业机械手笛卡尔轨迹跟踪逆运动学算法。
6.为实现上述目的，本发明采用以下技术方案：
7.偏置腕6r工业机械手笛卡尔轨迹跟踪逆运动学算法，所述6r工业机械手包括关节1到关节6，在连杆坐标系中建立坐标系{1}到坐标系{6}，每个坐标系由xi，zi表示，关节之间的连杆长度表示为a，连杆偏移量表示为d，转动关节之间的角度变量为θ1到θ6；
8.包括以下步骤：
9.s1、首先，采用改进的断开和重新连接方法，得到了仅包含θ6的非线性方程组和其他关节变量的解析公式，θ6为关节6的关节夹角；
10.将所有齐次变换矩阵相乘，得到末端执行器相对于基座的正向运动学公式：
[0011][0012]
使用tcf姿态标定方法测得机械手的末端姿势，则上述表达式可以写成：
[0013]
[0014]
改进的断开与重新连接方法：在连接坐标系{4}的原点处将机械手切割成两个子链。两个子链的正向运动学公式如下：
[0015]
t
l
＝t1(θ1)t2(θ2)t3(θ3)t4(θ4)rot(-α4，x4)
[0016][0017]
上式表示将原机器人分解为两个子链，子链l的末端位姿为t
l
，它由关节2的原点至关节4和关节5的轴线交点部分组成，是一个平面结构；其余部分组成子链r，其末端位姿为tr，其关节1和关节6之间的原点由t表示的虚拟连杆连接；在子链末端处，只要两子链的位姿满足以下条件即可重连：
[0018]
p
l
＝pr[0019][0020][0021][0022]
上述四个等式中，第一个等式实际上包括三个等式。β是第四和第五关节轴之间的角度。第一个等式及第二个等式中仅包括θ1、θ2、θ3和θ6。由它们可以导出只包含θ6的非线性方程组。第三个等式可用于求θ4，第四个等式可用于求θ5。机械手的六个关节变量满足以上四个等式后，两个子链可以重新连接到原来的六自由度结构中。
[0023]
s2、使用奇异轨迹将前三个关节的关节空间划分为四个唯一区域，建立了它们与逆运动学公式中k1，k2正负号之间的关系。
[0024]
等式|j|＝-a2p
n1
p
n2
，p
n1
＝a1+d4c
23-a3s
23-a2s2，p
n2
＝d4c
3-a3s3，c
23
为cos(θ2+θ3)缩写，s
23
为sin(θ2+θ3)缩写，s2为sin(θ2)缩写，c3为cos(θ2)缩写，s3为sin(θ3)缩写，其它缩写同理。可用于将θ2和θ3划分为四个子空间，每个子空间只有一个唯一的ik解，将表1中的d-h参数代入等式，得到四个唯一域(ud)，表2中的不等式可以确定每个唯一域的范围。
[0025]
表1机械手的d-h参数
[0026][0027]
表2唯一域的划分方法
[0028][0029]
通过将公式a1+d4c
23-a3s
23-a2s2＝k与表2进行比较，如
果p
n1
＜0，则k1＝-1，否则k1＝1。式＝1。式中，当k2＝1时，θ3的范围与p
n2
＞0的范围相同，两者部是θ3∈[-π/2，π/2]-atan(a3/d4)。因此，可以得到k1和k2与唯一域的对应关系，如表3所示：
[0030]
表3 k1和k2与唯一域之间的对应关系
[0031][0032]
s3、结合黄金分割法和对分法设计了一种求解一维非线性方程根的算法；
[0033]
s4、进行数值验证。
[0034]
进一步地，在步骤s1中单个接头的齐次变换矩阵可以表示为：
[0035][0036]
其中：
[0037]
θi——x
i-1
轴和xi轴之间关于z
i-1
的夹角；
[0038]di
——x
i-1
轴沿着z
i-1
轴到xi轴的距离；
[0039]ai
——沿着x
i-1
轴，z
i-1
轴和zi轴之间的距离；
[0040]
αi——z
i-1
轴和zi轴之间关于x
i-1
的夹角。
[0041]
进一步地，在步骤s1中采用以下方法推导关于θ6的非线性方程组：
[0042]
首先，将表1中机械手的d-h符号参数代入两个子链的正向运动学公式，并从式p
l
＝pr中得到三个方程式：
[0043]
c1(a1+d4c
23-a3s
23-a2s2)＝p1[0044]
s1(a1+d4c
23-a3s
23-a2s2)＝p2[0045]
d1+d4s
23
+a3c
23
+a2c2＝p3[0046]
其中：p1＝p
x-a
xd6-a
x
d5c
β
+(o
x
c6+n
x
s6)d5s
β
，
[0047]
p2＝p
y-a
yd6-ayd5c
β
+(oyc6+nys6)d5s
β
，
[0048]
p3＝p
z-a
xd6-azd5c
β
+(ozc6+nzs6)d5s
β
。
[0049]
si，ci，s
ij
，和c
ij
分别是sinθi，cosθi，sin(θi+θj)，和cos(θi+θj)的缩写形式。
[0050]
求等式c1(a1+d4c
23-a3s
23-a2s2)＝p1及s1(a1+d4c
23-a3s
23-a2s2)＝p2的平方和：
[0051]
a1+d4c
23-a3s
23-a2s2＝k
[0052][0053]
移动等式d1+d4s
23
+a3c
23
+a2c2＝p3和a1+d4c
23-a3s
23-a2s2＝k中除θ2以外的项到右边，然后求和的平方：
[0054]
as
23
+bc
23
＝e
[0055]
其中：a＝2a3(k-a1)+2d4(d
1-p3)，
[0056]
b＝2a3(d
1-p3)+2d4(a
1-k)，
[0057][0058]
通过将等式a1+d4c
23-a3s
23-a2s2＝k反向替换回等式c1(a1+d4c
23-a3s
23-a2s2)＝p1和s1(a1+d4c
23-a3s
23-a2s2)＝p2中获得：
[0059]
s1＝p2/k
[0060]
c1＝p1/k
[0061]
替换等式s1＝p2/k和c1＝p1/k进入式0
°
＜α4＜180
°
中得到：
[0062]
cs
23
+dc
23
＝f
[0063]
其中：c＝c
23
k，
[0064]
d＝a
23
p1+b
23
p3，
[0065]
f＝kc
β
，
[0066]a23
＝a
xcβ-(o
x
c6+n
x
s6)s
β
，
[0067]b23
＝a
ycβ-(oyc6+nys6)s
β
，
[0068]c23
＝a
zcβ-(ozc6+nzs6)s
β
。
[0069]
进一步地，在步骤s1中：将(θ2+θ3)作为一个整体，方程as
23
+bc
23
＝e和cs
23
+dc
23
＝f中只有两个变量，(θ2+θ3)和θ6，加上一个三角恒等式，从中导出只包含θ6的非线性方程
[0070]
f(θ6)＝(de-bf)2+(af-ce)
2-(ad-bc)2[0071]
由于k1的正负号，上述等式中有两个非线性方程。
[0072]
进一步地，在步骤s1中其余关节变量的ik解决方案为：
[0073]
θ6已解，那么：
[0074]
θ1＝atan2(s1，c1)；θ2＝atan2(s2，c2)；
[0075]
θ4＝atan2(0，-s
β
)+atan2(b4，a4)；θ5＝atan2(0，s
β
)+atan2(b5，a5)。
[0076]
本发明的有益效果为：相比于一般传统的6r工业机械手轨迹跟踪逆运动学求解的方法，本发明中的解法具有更明确的几何意义，推导过程更加便捷，满足实时、高精度及稳定性的要求。
附图说明
[0077]
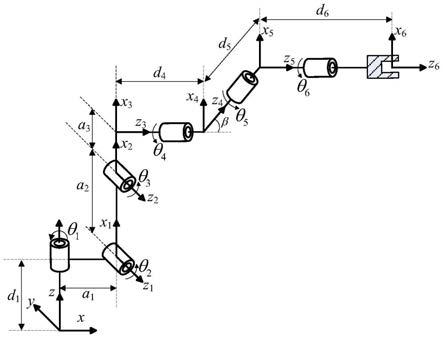
图1为手腕斜偏置工业机器人连杆坐标系；
[0078]
图2为四个唯一域；
[0079]
图3为初始搜索点的可能位置；
[0080]
图4为二分法流程图，表示为bisection()；
[0081]
图5为两个闭合根的选择算法流程图，表示为select_algo()；
[0082]
图6为组合算法的流程图，表示为comb_algo()；
[0083]
图7为完整ik算法的流程图，表示为complete_ik_algo()；
[0084]
图8为笛卡尔空间中轨迹跟踪的可视化；
[0085]
图9(a)为ik解和目标姿势之间的位姿误差范数；
[0086]
图9(b)为每个采样姿势的计算时间；
[0087]
图10为各位姿对应的关节位置曲线。
具体实施方式
[0088]
下面结合具体实施方式对本发明作进一步的说明。
[0089]
偏置腕6r工业机械手笛卡尔轨迹跟踪逆运动学算法：
[0090]
s1、以motoman-epx2050工业机器人为研究对象。该机器人手腕存在斜偏置，在非球腕工业机器人中比较特殊，解决了它的逆运动学问题，其它手腕偏置型工业机器人的逆运动学问题都可得到解决。表1列举了该机器人的d-h参数，表中β＝60
°
。
[0091]
表1工业机器人的d-h参数
[0092][0093]
单个接头的齐次变换矩阵表示为：
[0094][0095]
θi——x
i-1
轴和xi轴之间关于z
i-1
的夹角；
[0096]di
——x
i-1
轴沿着z
i-1
轴到xi轴的距离；
[0097]ai
——沿着x
i-1
轴，z
i-1
轴和zi轴之间的距离；
[0098]
αi——z
i-1
轴和zi轴之间关于x
i-1
的夹角。
[0099]
将所有齐次变换矩阵相乘，得到末端执行器相对于基座的正向运动学公式。
[0100][0101]
使用 姿态标定方法测得机械手的末端姿势，则上述表达式可以写成
[0102]
[0103]
在坐标系{4}的原点处将机械手切割成两个子链。两个子链的正向运动学公式如下
[0104][0105]
断开重新连接方法：上式表示将原机器人分解为两个子链，子链l的末端位姿为t
l
，它由关节2的原点至关节4和关节5的轴线交点部分组成，是一个平面结构；其余部分组成子链r，其末端位姿为tr，其关节1和关节6之间的原点由t表示的虚拟连杆连接；在子链末端处，当两子链的位姿满足以下条件即可重连：
[0106]
p
l
＝prꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0107][0108][0109][0110]
等式(5)包括三个等式。β是第四和第五关节轴之间的角度。等式(5)及(6)中仅包括θ1，θ2，θ3和θ6。由它们可以导出只包含θ6的非线性方程组。式(7)可用于求θ4，式(8)可用于求θ5。机械手的六个关节变量满足等式(5-8)后，两个子链可以重新连接到原来的六自由度结构中。
[0111]
首先，将表1中机械手的d-h符号参数代入式(4)，并从式(5)中得到三个方程式
[0112]
c1(a1+d4c
23-a3s
23-a2s2)＝p1ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0113]
s1(a1+d4c
23-a3s
23-a2s2)＝p2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0114]
d1+d4s
23
+a3c
23
+a2c2＝p3ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0115]
其中：p1＝p
x-a
xd6-a
x
d5c
β
+(o
x
c6+n
x
s6)d5s
β
，
[0116]
p2＝p
y-a
yd6-atd5c
β
+(oyc6+nys6)d5s
β
，
[0117]
p3＝p
z-a
zd6-azd5c
β
+(ozc6+nzs6)d5s
β
。
[0118]
si，ci，s
ij
，和c
ij
分别是sinθi，cosθi，sin(θi+θj)，和cos(θi+θj)的缩写形式。
[0119]
求等式(9)及(10)的平方和
[0120]
a1+d4c
23-a3s
23-a2s2＝k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0121][0122]
移动等式(11)和(12)中除θ2以外的项到右边，然后求和的平方
[0123]
as
23
+bc
23
＝e
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0124]
其中：a＝2a3(k-a1)+2d4(d
1-p3)，
[0125]
b＝2a3(d
1-p3)+2d4(a
1-k)，
[0126][0127]
通过将等式(12)反向替换回等式(9)和(10)获得
[0128]
s1＝p2/k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0129]
c1＝p1/k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0130]
替换等式(14)和(15)进入式(6)得到
[0131]
cs
23
+dc
23
＝f
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0132]
其中：c＝c
23
k，
[0133]
d＝a
23
p1+b
23
p3，
[0134]
f＝kc
β
，
[0135]a23
＝a
xcβ-(o
x
c6+n
x
s6)s
β
，
[0136]b23
＝a
ycβ-(oyc6+nys6)s
β
，
[0137]c23
＝a
zcβ-(ozc6+nzs6)s
β
。
[0138]
将(θ2+θ3)作为一个整体，方程(13)和(16)只有两个变量，(θ2+θ3)和θ6，加上一个三角恒等式，从中导出只包含θ6的非线性方程
[0139]
f(θ6)＝(de-bf)2+(af-ce)
2-(ad-bc)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0140]
由于k1的正负号，等式(17)中有两个非线性方程。
[0141]
θ6已解，θ1直接由等式(14)及(15)得到
[0142]
θ1＝atan2(s1，c1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0143]
(11)将和(12)移动到方程的右侧，然后将它们的平方和，可以得到θ3[0144][0145]
k2＝
±
1，
[0146]
得到θ3后，将其代入等式(11)和(12)并将其视为一阶方程的二元系统，以获得θ2，
[0147]
θ2＝atan2(s2，c2)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(20)
[0148]
其中：
[0149][0150]
在得到θ1，θ2，θ3，和θ6后，可以唯一地确定θ4和θ5。θ4可以通过式(7)来解决
[0151]
θ4＝atan2(0，-s
β
)+atan2(b4，a4)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(21)
[0152]
其中：a4＝a
23s1-b
23
c1，
[0153]
b4＝c1s
23a23-c
23c23
+s1s
23b23
。
[0154]
θ5可由式(8)确定
[0155]
θ5＝atan2(0，s
β
)+atan2(b5，a5)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22)
[0156]
其中：a5＝c
23
(c1(n
xc6-o
x
s6)+s1(n
yc6-oys6))+s
23
(n
zc6-ozs6)，
[0157][0158]
s2、以θ6为常数，微分式(9～11)中的θ1，θ2，和θ3，得到子链l的雅可比矩阵。从而得到雅可比矩阵的行列式
[0159]
|j|＝-a2p
n1
pnꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(23)
[0160]
其中：p
n1
＝a1+d4c
23-a3s
23-a2s2，
[0161]
p
n2
＝d4c
3-a3s3。
[0162]
等式(23)可用于将θ2和θ3划分为四个子空间，每个子空间只有一个唯一的ik解，将表1中的d-h参数代入等式，得到四个唯一域(ud)，如图2所示，在图2中，绿线表示|j|＝0时获得的奇点轨迹，表2中的不等式可以确定图2中的每个唯一域。
[0163]
表2唯一域的划分方法
[0164][0165]
现在考虑k1和k2的正负号和唯一域之间的关系。通过将公式(12)与表2进行比较，可以清楚地看到，如果p
n1
＜0，则k1＝-1，否则k1＝1。式(19)中，当k2＝1时，θ3的范围与p
n2
＞0的范围相同，两者都是θ3∈[-π/2，π/2]-atan(a3/d4)。因此，可以得到k1和k2与唯一域的对应关系，如表3所示：
[0166]
表3 k1和k2与唯一域之间的对应关系
[0167][0168]
机械手只需要一组ik解就可以在笛卡尔空间中完成轨迹跟踪任务。假设轨迹上有两个相邻的点，它们的位姿误差很小，然后将两点之间的姿态变换视为微分运动，从差动运动可以看出，它们之间的关节误差也很小，从图2中每个唯一域的分布可以看出，只有当相邻姿势的ik解在同一唯一域中时，它们之间的关节误差才会始终很小，它符合机械手ik多解选择方法中的最小位移原则，因此在同一唯一域中的相邻点之间选择ik解决方案，即当前时刻ik解决方案中的k1和k2可以由基于表2和表3的相邻点的ik解决方案确定。
[0169]
s3、考虑到机械手末端在笛卡尔空间中跟踪轨迹，将前一姿态的已知θ6作为初始搜索点，设计一种一维局部搜索算法。
[0170]
一种求解一维非线性方程根的算法：由于给定的初始搜索点是相邻位置的ik解，因此它将接近当前姿势的ik解，初始搜索点和非线性方程根之间可能有四种方位关系，如图3所示，在图中x1，x2，x3，和x4表示非线性方程的根，黑色框表示初始搜索点可能出现的位置。
[0171]
在找到根之前，需要确定搜索间隔，因此搜索方向至关重要，从图中可以看出，沿水平方向和垂直方向有两个变化方向，即沿轴的正向和反向。
[0172]
首先，当θ6改变时，非线性方程的值总是在负方向上改变，等式(17)可以改写为
[0173][0174]
接下来，沿θ6轴的变化方向可确定如下：
[0175][0176]
其中ε是一个极小的正数。
[0177]
那么，θ6可以根据下面的公式进行迭代，
[0178]
[0179]
其中k是迭代次数，h是步长。
[0180]
一维连续非线性方程的根只有两种形式，如图3所示，形式一是x1和x2，根部之间有波谷(或波峰)，形式二是x3和x4，其中波谷(或波峰)的顶点是方程的根。
[0181]
形式一的算法：上述计算结果表明，唯一域方法可以获得在跟踪轨迹上前三个相邻点之间的最小距离的ik解，从上述的公式可以推断，其他四个关节变量确定θ4和θ5，所以需要找到最接近初始θ6的非线性方程的根，找到f(θ
6k-1
，ky)f(θ
6k
，ky)＜0的区间[min{θ
6k-1
，θ
6k
}，max{θ
6k-1
，θ
6k
}]，使用二分法确定根，该算法如图4所示，由于以下算法提供的间隔可能没有根，因此在图中将判断条件fafc＞0添加到原始的二分法中。
[0182]
当方程的两个根非常接近时，距离初始搜索点最近的根不一定是目标解，原因是虽然θ3的符号被消除，但它与非线性方程耦合，因此当两个根彼此非常接近时，与初始搜索点附近的根对应的θ2和θ3可能与初始搜索点的θ2和θ3不在同一唯一域中，因此需要设计一种算法，以便在两个根接近时在它们之间进行选择，如图5所示，在图中函数all_ik()由等式(18-22)组成，其输入为θ6，k1和k2，其输出为六个关节变量的一组ik解，函数fit()仅由公式(16)组成，它与输入θ1，θ2，θ3和θ6一起工作，由于方程中每个根获得的θ2和θ3具有唯一对应的k1和k2，因此最终可以使用fit()确定根选择。
[0183]
形式二的算法：在根存在的第二种形式中，区间不能由f(θ
6k-1
，ky)f(θ
6k
，ky)＜0来确定，当搜索步长大于相邻两个根之间的距离时，该方法也会失败，在这种情况下，可以使用f(θ
6k-1
，ky)＜f(θ
6k
，ky)来确定搜索间隔，找到根的组合算法如图6所示，在图中，当区间中仅存在重复根时，可通过激活黄金分割法直接找到，然而重复根更可能作为两个非常接近的根存在，因此黄金分割法也可以用来寻找θ6，它对应于两个非常接近的根之间的负f(θ6，ky)，然后可以使用select_algo()算法选择最终ik解决方案。
[0184]
前面的内容介绍了ik算法的关键细节，接下来将它们串联起来作为一个完整的算法，如图7所示，在图中，θ
20
，θ
30
和θ
60
通常是前一个姿势的ik解，当机械手从起始位置移动时，它们都默认为零，ε用于确定θ6的搜索方向k
dir
，由于可能有两个彼此非常接近的根，ε的值应小于e2，在区间确定期间，迭代的θ6可能正好是方程的根，因此e1也可以设置为小于e2的值，需要注意的是，当区间的端点满足f(θ
6k-1
，ky)f(θ
6k
，ky)＜0时，不直接使用对分法求解，而是使用select_algo()算法，原因是当相邻根足够近时，定义间隔的端点可能位于它们之间。
[0185]
s4、为检验本文所提算法的性能，在仿真环境下展开试验，该算法在笔记本电脑平台(windows10 professional 64位，英特尔)上的matlb2018b中编译coretm i7-9750h，@2.60ghz cpu，8.00gb ddr4 2666mhz ram)。
[0186]
仿真实验过程中，机械手需要在笛卡尔空间中跟踪球形螺旋线，其参数方程如下：
[0187]
[0188]
其中：t0＝5.01∶0.01∶125。
[0189]
使用笛卡尔空间中的五次多项式插值，获得从机械手起始位置到球面螺旋起点的轨迹，
[0190][0191]
其中：t＝0∶0.01∶5。
[0192]
轨迹由等式(27)和(28)组成，如图8所示，轨迹上每个点的姿态始终与θ＝[0，0，0，0，0，0]处的姿态相同，然后使用图7中complete_ik_algo()算法来求解每个姿势的ik，初始化ε＝10-15
，e1＝10-16
，e2＝10-14
，h＝π/180。θ
20
，θ
30
和θ
60
的输入值在第一个姿势时设置为零，然后使用前一个姿势的ik解作为其值。
[0193]
图8显示了motoman-epx2050机械手在simulink中跟踪笛卡尔空间轨迹，图中的轨迹由等式(27)和(28)获得的12501个点组成，图9显示了使用complete_ik_algo()算法求解这些点的ik的结果，在图9(a)中，最大值为4.04
×
10-12
mm，最小值为1.65
×
10-13
mm，平均值为1.58
×
10-12
mm，标准偏差为8.60
×
10-13
mm，在图9(b)中，最大值为0.0648ms，最小值为0.0117ms，平均值为0.0137ms，标准偏差为0.0024ms，图10显示了每个接头的位移。
[0194]
本文的方法在公式推导过程中有更明确的几何意义，本文采用固定的初始迭代点，算法在固定运行次数内便可求出所有逆解；同时本文的方法具有更强的理论推广性，同时给出了其他关节角的具体求解方法；本文算法部分所使用的算法易于编程实现。
[0195]
以上所述实例仅是为充分说明本发明而所举的较佳的实施例，本发明的保护范围不限于此，本技术领域的技术人员在本发明基础上所作的等同替代或变换，均在本发明的保护范围之内。