一种基于平滑切换的机械臂碰撞响应控制方法

1.本发明涉及碰撞响应领域，特别涉及一种基于平滑切换的机械臂碰撞响应控制方法。


背景技术：

2.机械臂是能模仿人类手臂功能完成各项作业任务的自动控制设备，具体有高精度、承受能力强、刚性强的特点。机械臂的运动都是按照接收到的指令进行的，因此并不具备灵敏检测以及响应外界碰撞的能力，所以在作业过程中极易会发生机械臂发生碰撞的情况，从而影响作业的安全性。合理的碰撞响应能力可保证机械臂自身及周围环境的安全，因此机械臂碰撞响应成为本领域的研究重点。
3.目前最简单的碰撞响应策略就是使机械臂停止或者朝着远离碰撞的方向运动。但是这种方法虽然保证了机械臂在遭到意外冲击时的安全性，但这种方式无法对人机交互场景进行合理响应。因此本领域的技术人员又提出了基于柔顺控制的碰撞响应策略，这种方法不仅能缓冲机械臂所受意外冲击力，还可确保人机交互的安全，是目前广泛使用的碰撞响应方法。但现有基于柔顺控制的碰撞响应方法通常在检测到碰撞后采用“硬切换”方式将控制模式从位置控制切换到柔顺控制，容易控制量突变甚至系统失稳的问题，从而导致碰撞响应方法难以实现控制状态平滑切换，进而影响机械臂的作业安全性。


技术实现要素：

4.本发明目的是为了解决目前的机械臂碰撞响应方法还无法实现控制状态的平滑切换，进而导致机械臂作业安全性低的问题，而提出了一种基于平滑切换的机械臂碰撞响应控制方法。
5.一种基于平滑切换的机械臂碰撞响应控制方法具体过程为：
6.步骤一、建立机械臂动力学回归模型；
7.步骤二、设计机械臂的阈函数β(τ
ext
)，并根据阈函数β(τ
ext
)获取机械臂平滑切换函数ω；
8.步骤三、根据步骤二设计的平滑切换函数获取机械臂关节控制力矩；
9.步骤四、将步骤三获得的机械臂关节控制力矩代入步骤一建立的机械臂动力学回归模型中，获取机械臂碰撞的平滑切换方式：
10.若机械臂没有受到外力则阈函数β(τ
ext
)＜0，平滑切换函数ω＝1，机械臂则在位置控制模式下工作，若机械臂受到外力作用则阈函数β(τ
ext
)＞0，平滑切换函数ω＝0，机械臂则在柔顺控制模式下工作。
11.本发明的有益效果为：
12.本发明提出的碰撞响应方法使机械臂在发生碰撞后可以做出合理响应，为机械臂及周围环境提供了安全保障。本发明通过设计可实现平滑切换的关节控制力矩解决了现有基于柔顺控制的碰撞响应方法采用“硬切换”方式所带来的控制量突变甚至系统失稳的问
题，确保了机械臂系统的稳定性。且本发明易于工程实现。
附图说明
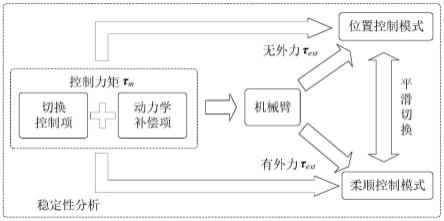
13.图1为本发明中机械臂碰撞响应的工作原理图；
14.图2为本发明的切换函数图形解释图。
具体实施方式
15.具体实施方式一：本实施方式一种基于平滑切换的机械臂碰撞响应控制方法具体过程为：
16.步骤一、建立机械臂动力学回归模型；
17.步骤二、设计机械臂的阈函数β(τ
ext
)，并根据阈函数β(τ
ext
)获取机械臂平滑切换函数ω；
18.步骤三、根据步骤二设计的平滑切换函数获取机械臂关节控制力矩；
19.步骤四、将步骤三获得机械臂关节控制力矩代入步骤一建立的机械臂动力学回归模型中，获取机械臂碰撞的响应方式：
20.判断机械臂是否受到外力作用，若机械臂没有受到外力则阈函数β(τ
ext
)＜0，平滑切换函数ω＝1，机械臂则在位置控制模式下工作，若机械臂受到外力作用则阈函数β(τ
ext
)＞0，平滑切换函数ω＝0，机械臂则在柔顺控制模式下工作；
21.步骤五、验证机械臂系在没有受到外力时在位置控制模式下工作以及机械臂系统受到外力在柔顺控制模式下工作是否稳定。
22.具体实施方式二：所述步骤一中的建立机械臂动力学回归模型，如下：
23.利用牛顿拉格朗日法建立机械臂动力学模型并对模型进行线性化，具体如下：
[0024][0025]
其中，q，分别为机械臂关节位置、速度、加速度；m(q)，d，g(q)分别为机械臂的惯量矩阵、粘性摩擦矩阵、重力向量；为机械臂的科氏力和向心力矩阵；为机械臂关于的回归矩阵；p为机械臂动力学参数向量；τm，τ
ext
分别为机械臂关节控制力矩和所受外力矩。
[0026]
具体实施方式三：所述步骤二中的设计机械臂的阈函数β(τ
ext
)，并根据阈函数β(τ
ext
)获取机械臂平滑切换函数ω，具体包括以下步骤；
[0027]
步骤二一、设计机械臂的阈函数β(τ
ext
)，如下式：
[0028][0029]
其中，ri为机械臂第i个关节的阈值，是人为设定的，取值范围通常为0.3～0.5，i∈[1,n]是机械臂关节的标号，n是机械臂关节的总数量，τ
ex
t
,i
为τ
ext
的第i个分量，即机械臂第i个关节所受力矩；
[0030]
步骤二二、根据阈函数β(τ
ext
)获取机械臂平滑切换函数：
[0031][0032]
其中，κ为切换函数；
[0033]
当阈函数β(τ
ext
)＜0，切换函数ω＝1；当阈函数β(τ
ext
)＞0，切换函数ω＝0。由公式(3)可知，切换函数ω是二阶连续的，因此ω在0和1之间的切换是平滑的。
[0034]
其中，当τ
ext
的任一分量大于对应预设关节阈值(任一机械臂关节所受外力矩大于对应预设关节阈值)时，阈函数β(τ
ext
)的值大于零；当τ
ext
的所有分量都小于对应的预设关节阈值(机械臂中所有关节所受外力矩小于对应预设关机阈值)时，阈函数β(τ
ext
)的值小于零。
[0035]
具体实施方式四：所述步骤三中的根据步骤二设计的平滑切换函数获取机械臂关节控制力矩，包括以下步骤：
[0036]
步骤三一、根据步骤二获得的平滑切换函数定义机械臂参考速度向量：
[0037][0038]
其中，qd为机械臂期望跟踪位置，eq＝q-qd为机械臂位置误差，λq为位置误差系数，为大于0的常数，是为机械臂期望跟踪速度。
[0039]
步骤三二、利用步骤三一获得的机械臂参考速度向量定义机械臂滑动向量：
[0040][0041]
步骤三三、利用步骤三一获得的机械臂参考速度向量和机械臂滑动向量获取机械臂关节控制力矩：
[0042][0043]
其中，k为正定对角矩阵；为机械臂关于的回归矩阵；为机械臂动力学参数向量p的估计向量，为机械臂参考加速度向量。
[0044]
所述机械臂关节控制力矩为切换控制项和动力学补偿项之和；
[0045]
所述通过如下自适应律进行更新：
[0046][0047]
其中，г为正定矩阵，()
t
是转置。
[0048]
具体实施方式五：所述步骤四中的将步骤三获得机械臂关节控制力矩代入步骤一建立的机械臂动力学回归模型中，获取机械臂碰撞的响应方式，包括以下步骤：
[0049]
步骤四一、将步骤三获得的械臂关节控制力矩代入步骤一建立的机械臂动力学回归模型，获得改写后的机械臂动力学模型：
[0050]
首先，将公式(6)带入到公式(1)可得到机械臂动力学模型的改写形式：
[0051][0052]
然后，公式(8)可进一步改写为：
[0053]
[0054]
其中，为机械臂动力学参数估计误差，
[0055]
步骤四二、定义lyapunov函数，并将步骤四一获得的机械臂所受外力代入到lyapunov函数中，具体如下：
[0056]
首先，定义如下lyapunov函数：
[0057][0058]
对公式(10)求导可得lyapunov函数的导数：
[0059][0060]
然后，将公式(9)所表示的动力学模型改写式带入公式(11)，将lyapunov函数的导数进一步改写为：
[0061][0062]
步骤四三、将公式(7)所表示自适应律代入到公式(12)中，可进一步简化lyapunov函数的导数为：：
[0063][0064]
其中，是中间变量；
[0065]
步骤四四、根据步骤四三获得的公式(13)确定机械臂在没有受到外力作用时的工作模式：
[0066]
首先，由于机械臂不受外力(τ
ext
＝0、ω＝1)，公式(13)所表示的lyapunov函数的导数可改写为：
[0067][0068]
由公式(14)可知，机械臂系统的lyapunov函数的导数小于等于零，系统是稳定的。
[0069]
然后，由于v＞0，则v有界。由公式(10)所表示的机械臂系统的lyapunov函数可知e
sq
和有界；由于e
sq
和有界，根据公式(9)所表示的机械臂动力学模型中可知有界；由于e
sq
和有界，则esq一致连续。由公式(14)所表示的lyapunov函数的导数可得：
[0070][0071]
其中，t是时间，λ
min
[d+k]为矩阵d+k的最小特征值，v(0)和v(+∞)分别表示机械臂系统在0时刻和+∞时刻的lyapunov函数；
[0072]
由于v(0)-v(+∞)有界，根据积分公式(15)可知：
[0073][0074]
公式(16)表示e
sq
收敛，再由公式(5)所表示的机械臂滑动向量可知：
[0075][0076]
公式(17)表示机械臂位置误差eq收敛于0(eq＝q-qd)，机械臂运动位置收敛于期望位置，机械臂工作在位置控制模式下。
[0077]
步骤四五、根据机械臂关节控制力矩确定机械臂在受到外力作用时的工作模式：
[0078]
步骤四五一、由于机械臂在受到外力时τ
ext
≠0、ω＝0，因此根据公式(4)所表示的机械臂参考速度向量可得到下式：
[0079][0080]
步骤四五二、根据机械臂动力学回归模型的具体形式和公式(18)可得到如下等式：
[0081][0082]
其中，和分别为m(q)，d，g(q)和的估计值；机械臂动力学回归模型的具体形式为：
[0083]
步骤四五三、采用公式(7)所表示的自适应律使和分别收敛于m(q)，d，g(q)和因此公式(19)可进一步简化为：
[0084][0085]
步骤四五四、根据公式(20)和ω＝0，公式(6)所表示的机械臂关节控制力矩可简化为τm＝g(q)。再将τm＝g(q)带入公式(1)所表示的机械臂动力学回归模型可获得下式：
[0086][0087]
由公式(21)可以看出，当受外力作用时，机械臂可视为由外力矩驱动的阻尼系统，处于柔顺控制模式。
[0088]
具体实施方式六：所述步骤五中的验证机械臂系在没有受到外力时在位置控制模式下工作以及机械臂系统受到外力在柔顺控制模式下工作是否稳定：
[0089]
步骤五一、验证机械臂系统没有受到外力时在位置控制模式下工作是否稳定：
[0090]
由公式(14)可知，机械臂系统在没有受到外力时在位置控制模式下工作是稳定的；
[0091]
步骤五二、验证机械臂系统受到外力时在柔顺控制模式下工作是否稳定：
[0092]
对公式(13)积分可得：
[0093][0094]
其中，t为时间；ε为积分因子。
[0095]
由于根据公式(22)可得：
[0096][0097]
由于τ
ext
有界，则有如下不等式成立：
[0098][0099]
根据公式(22)和公式(24)可得：
[0100][0101]
由可知：
[0102]
q≥λ
min
[dq]||e
sq
||2ꢀꢀ
(26)
[0103]
将公式(26)带入公式(25)可得：
[0104][0105]
由公式(27)可知e
sq
有界。由于e
sq
有界，由公式(23)可知v有界。再由公式(10)所表示的机械臂的lyapunov函数可知有界。至此，机械臂系统所有的状态量均可证明有界，机械臂系统是稳定的。
[0106]
需特殊强调的是：由于切换函数ω是连续的，因此机械臂可在位置控制和柔顺控制之间进行平滑切换。
[0107]
以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的一般技术人员来说，依据本发明的思想，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。