双层自聚焦透镜阵列的制作方法

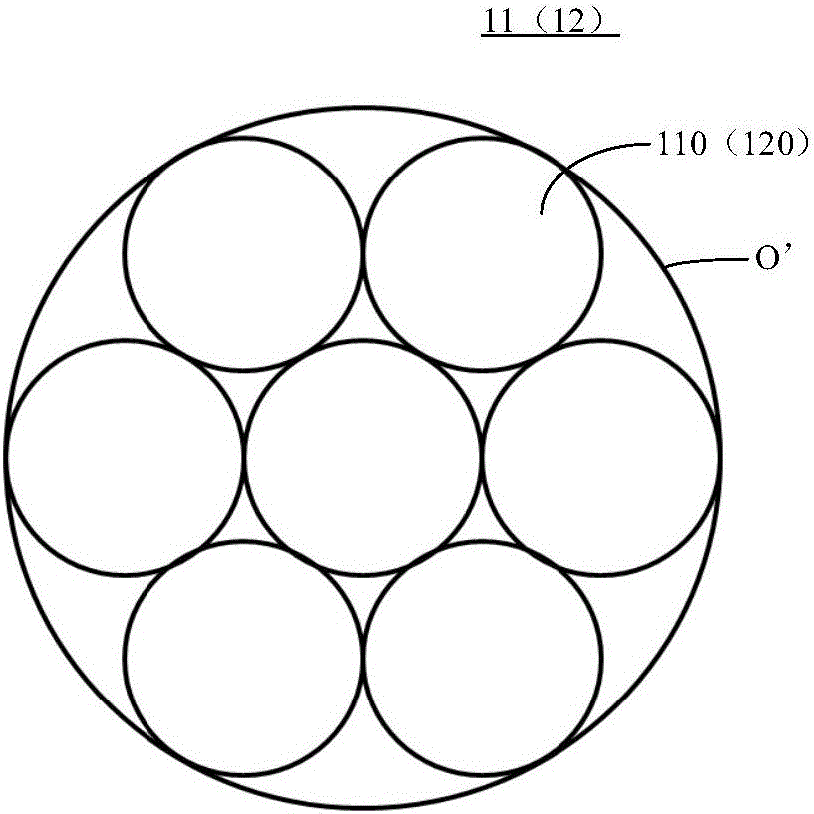
本发明涉及光学聚焦系统，尤其涉及双层自聚焦透镜阵列。

背景技术：

自由空间光通信(FSO)，又称为无线光通信或者大气光通信，主要包含星间光通信，星地光通信及地面激光通信等。光纤具有体积小、重量轻等优点，并且可以利用高灵敏度和高放大倍数的放大器放大光纤中传输的光信号，这些优势使得光纤能够改善空间光接收装置的性能。

随着光纤技术的发展，空间光-光纤的耦合技术己经被广泛运用于各领域，如光纤传感、生物光子学、激光雷达等。由于单模光纤的性能好，而且大部分光器件都是基于单模光纤的，因此将空间光耦合到单模光纤中能够更加方便地实现高灵敏度的相干接收、低噪声的光信号放大以及高性能的光滤波。

但是自由空间光通信中，无论是在地面短距离激光通信还是卫星光通信，都将面临的重大挑战之一是大气湍流对光通信的影响，大气湍流引起的光场振幅起伏以及光束漂移效应会使得接收孔径接收到的光强发生起伏，使得耦合进光纤的光强不稳定。到达角起伏效应使得接收面上耦合角度大于临界角的光线增多，即耦合进光纤的功率大幅下降。波前相位起伏会使得光场的空间相干性发生退化，使空间光到单模光纤的耦合效率降低并产生起伏，这些起伏可导致突发性通信错误,以至于通信中断。这些效应将严重降低光束的传输质量，进而限制激光通信系统的通信性能和激光链路的可靠性，因此，在应用光纤通信技术的空间激光链路中，大气湍流对空间光到单模光纤耦合效率影响是必须考虑的重要因素。

已知现有技术出现了小口径透镜阵列型的空间光-单模光纤耦合结构，耦合效果较好，而且耦合效率随着耦合距离的增加不断减小，相比较单透镜而言在长距离的传输中表现出了明显的优势，但是此种结构未考虑到像差的存在以及偏移对耦合效率的影响。

技术实现要素：

本发明的目的在于，解决像差和偏移对空间光通信中耦合效率的不利影响。

本发明的目的是采用以下技术方案来实现的。

一种双层自聚焦透镜阵列，包括：第一层自聚焦透镜阵列，包括多个紧密排列、结构相同、主光轴平行的第一自聚焦透镜元；第二层自聚焦透镜阵列，位于所述第一层自聚焦透镜阵列的下方，包括多个紧密排列、结构相同、主光轴平行的第二自聚焦透镜元，所述第二自聚焦透镜元与所述第一自聚焦透镜元的数量相同、直径相等、位置对应且主光轴重合；多条耦合光纤，每条耦合光纤与每个所述第二自聚焦透镜元一对一地耦合，以使信号光依次经过所述第一层自聚焦透镜阵列、第二层自聚焦透镜阵列后进入所述耦合光纤；以及连接部，用于连接所述第一层和第二层自聚焦透镜阵列。

相较于现有技术，本发明提供的双层自聚焦透镜阵列既缩小了光斑尺寸也尽量减小了发散角，具有更好的偏移容忍度，在大气湍流中也具有较好的抑制湍流的作用，在传输同样距离的情况下，双自聚焦透镜阵列的耦合效率下降更缓慢，在长距离传输中表现出了良好的优势。

上述说明仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，而可依照说明书的内容予以实施，并且为了让本发明的上述和其他目的、特征和优点能够更明显易懂，以下特举较佳实施例，并配合附图，详细说明如下。

附图说明

图1是本发明第一实施例提供的双层自聚焦透镜阵列的结构示意图。

图2是本发明第一实施例提供的双层自聚焦透镜阵列其中一层自聚焦透镜阵列的平面示意图。

图3是本发明第一实施例提供的双层自聚焦透镜阵列的第一、第二自聚焦透镜元的结构及光路图。

图4是本发明第一实施例提供的双层自聚焦透镜阵列的耦合曲线示意图。

图5是本发明第二实施例提供的双层自聚焦透镜阵列的第一、第二自聚焦透镜元的结构示意图。

图6是本发明第三实施例提供的双层自聚焦透镜阵列结构示意图。

具体实施方式

为了便于理解本发明，下面将参照相关附图对本发明进行更全面的描述。附图中给出了本发明的较佳实施方式。但是，本发明可以以许多不同的形式来实现，并不限于本文所描述的实施方式。相反地，提供这些实施方式的目的是使对本发明的公开内容理解的更加透彻全面。

除非另有定义，本文所使用的所有的技术和科学术语与属于本发明的技术领域的技术人员通常理解的含义相同。本文中在本发明的说明书中所使用的术语只是为了描述具体的实施方式的目的，不是旨在于限制本发明。本文所使用的术语“及/或”包括一个或多个相关的所列项目的任意的和所有的组合。

请参阅图1，本发明第一实施例提供的双层自聚焦透镜阵列10包括第一层自聚焦透镜阵列11、第二层自聚焦透镜阵列12、多条耦合光纤30以及连接部40。

第一层自聚焦透镜阵列11包括多个紧密排列、结构相同、主光轴平行的第一自聚焦透镜元110。第二层自聚焦透镜阵列12位于第一层自聚焦透镜阵列11的下方，包括多个紧密排列、结构相同、主光轴平行的第二自聚焦透镜元120，第二自聚焦透镜元120与第一自聚焦透镜元110的数量相同、位置对应且主光轴重合。多条耦合光纤30分别与每个第二自聚焦透镜元120耦合。连接部40用于连接第一层自聚焦透镜阵列11和第二层自聚焦透镜阵列12。在本实施例中，连接部40具体包括多个连接杆400，沿圆周均匀设置，粘接两个自聚焦透镜阵列。

请参阅图2，第一层自聚焦透镜阵列11包括至少7个按照六边形紧密排列的第一自聚焦透镜元110，第一层自聚焦透镜阵列11用于接收信号光，所述信号光可以是激光。第二层自聚焦透镜阵列12包括至少7个按照六边形紧密排列的第二自聚焦透镜元120。数量大于7个的自聚焦透镜元也依次按照六边形紧密排列，整个阵列形状类似蜂巢。

按照图2所示方式排列的自聚焦透镜元(包括第一和第二自聚焦透镜元)可以达到最大的占空比，从而避免不必要的耦合损耗，可以计算得出七个自聚焦透镜元所占的面积约为与其外切的大圆O’(相当于一个大透镜)的78％。

如图3所示，第一自聚焦透镜元110的入光面1101和出光面1102为平面，第二自聚焦透镜元120的入光面1201和出光面1202也均为平面。优选地，第一、第二自聚焦透镜元110、120的结构相同，这是指除了出光面和入光面的形状相同之外，还包括厚度、中心折射率、聚焦常数等参数均相同。优选地，本实施例选用1/4节距自聚焦透镜作为第一、第二自聚焦透镜元110、120。

在本实施例中，耦合光纤30具体包括7条单模光纤30。单模光纤30的入光面301与第二自聚焦透镜元120的出光面1202直接粘接，使得结构更紧凑、稳固，耦合效率更高。

信号光的光束L依次经过第一层自聚焦透镜阵列11、第二层自聚焦透镜阵列12后被会聚，然后进入单模光纤30。

为了达到理想耦合效果，需要光线以最佳位置出射，因此以下通过求解光线的出射位置来确定达到理想耦合效果的各项结构参数。

对于第一自聚焦透镜元110来说，由平行光入射条件，极限边光出射后的光线高度r₁及其向外光学方向余弦p₁为：

$r_1=\frac{D}{2}cos\left(\sqrt{A_1}{z}_1\right)---\left(1\right)$

$p_1=-\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}sin\left(\sqrt{A_1}{z}_1\right)---\left(2\right)$

对于第二自聚焦透镜120来说，利用逆光束求解，在第二自聚焦透镜120出光面轴上中心点处，令光线以向外光学方向余弦等于单模光纤数值孔径NA_f入射，即入射高度为0，入射角度余弦为单模光纤数值孔径NA_f，此处为能入射的最大角度，则在出射断面处即靠近第一自聚焦透镜110的出光面处，出射点r₂及向外方向余弦p₂分别为：

$r_2=\frac{{\mathrm{NA}}_f}{n_2\left(0\right)\sqrt{A_2}}sin\left(\sqrt{A_2}{z}_2\right)---\left(3\right)$

$p_2={\mathrm{NA}}_{f}cos\left(\sqrt{A_2}{z}_2\right)---\left(4\right)$

为满足入射条件，从第一自聚焦透镜110中出射的光线，与第二自聚焦透镜120的逆向光束的出射端面上的方向余弦的绝对值相等，即|p₁|＝|p₂|，代入式(4)所得方程组：

$z_2=\frac{\arcsin \sqrt{1-\frac{{\left(\frac{D}{2}{n}_1\right(0\left)\sqrt{A_1}\right)}^2}{{\left({\mathrm{NA}}_f\right)}^2}}{\sin }^2\left(\sqrt{A_1}{z}_1\right)}{\sqrt{A_2}}---\left(5\right)$

由于θ一般不是很大，由几何关系可知两自聚焦透镜之间的间距为：

$z_{\mathrm{\Δ}}=\frac{r_1-r_2}{\left|p_1\right|}---\left(6\right)$

由|p₁|＝|p₂|得到：

$sin\left(\sqrt{A_1}{z}_1\right)=\sqrt{1-{\left(\frac{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}sin\left(\sqrt{A_1}{z}_1\right)}{{\mathrm{NA}}_f}\right)}^2}---\left(7\right)$

为了求得使整个耦合结构更小的参数，将式(6)代入式(7)中，可以得到：

$z_{\mathrm{\Δ}}=\frac{\frac{D}{2}\cos \left(\sqrt{A_1}{z}_1\right)-\frac{{\mathrm{NA}}_f}{n_2\left(0\right)\sqrt{A_2}}\sqrt{1-{\left(\frac{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}\sin \left(\sqrt{A_1}{z}_1\right)}{{\mathrm{NA}}_f}\right)}^2}}{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}\sin \left(\sqrt{A_1}{z}_1\right)}---\left(8\right)$

将上式变形得到：

$z_{\mathrm{\Δ}}=\frac{\cot \left(\sqrt{A_1}{z}_1\right)}{n_1\left(0\right)\sqrt{A_1}}-\left(\frac{{\mathrm{NA}}_f}{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}{n}_2\left(0\right)\sqrt{A_2}}\right)\left(\sqrt{{\csc }^2\left(\sqrt{A_1}{z}_1\right)-{\left(\frac{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}}{{\mathrm{NA}}_f}\right)}^2}\right)---\left(9\right)$

对上式求导为零来求解，在上式中令将上式对x求导：

$\frac{{\mathrm{dz}}_{\mathrm{\Δ}}}{dx}=-\frac{{\csc }^2\left(\sqrt{A_1}{z}_1\right)}{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}}(\frac{D}{2}-\frac{\frac{{\mathrm{NA}}_f\cot \left(\sqrt{A_1}{z}_1\right)}{n_2\left(0\right)\sqrt{A_2}}}{\sqrt{{\csc }^2\left(\sqrt{A_1}{z}_1\right)-{\left(\frac{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}}{{\mathrm{NA}}_f}\right)}^2}})---\left(10\right)$

令此式为零，解出的值即为使得整个系统最小的z₁，由各项关系可得括号里的因子整体为0：

$\frac{D}{2}=\frac{\frac{{\mathrm{NA}}_f\cot \left(\sqrt{A_1}{z}_1\right)}{n_2\left(0\right)\sqrt{A_2}}}{\sqrt{{\csc }^2\left(\sqrt{A_1}{z}_1\right)-{\left(\frac{\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}}{{\mathrm{NA}}_f}\right)}^2}}---\left(11\right)$

得到z₁、z_Δ、z₂的值分别为：

$z_1=\frac{\arcsin \left({\mathrm{NA}}_f\sqrt{\frac{\frac{D^2}{4}-{\left(\frac{{\mathrm{NA}}_f}{n_2\left(0\right)\sqrt{A_2}}\right)}^2}{{\left(\frac{D^2}{4}{n}_1\right(0\left)\sqrt{A_1}\right)}^2-{\left(\frac{{\mathrm{NA}}_f^2}{n_2\left(0\right)\sqrt{A_2}}\right)}^2}}\right)}{\sqrt{A_1}}---\left(12\right)$

$z_{\mathrm{\Δ}}=\frac{2\sqrt{({\left(\frac{D}{2}{n}_1\left(0\right)\sqrt{A_1}\right)}^2-{\mathrm{NA}}_f^2)(\frac{D^2}{4}-{\left(\frac{{\mathrm{NA}}_f}{n_2\left(0\right)\sqrt{A_2}}\right)}^2)}}{{\mathrm{Dn}}_1\left(0\right)\sqrt{A_1}{\mathrm{NA}}_f}---\left(13\right)$

$z_2=\frac{\arcsin \left(\frac{{\mathrm{NA}}_f}{n_2\left(0\right)\sqrt{A_2}}\right)\sqrt{\frac{{\left(\frac{D}{2}{n}_1\right(0\left)\sqrt{A_1}\right)}^2-{\mathrm{NA}}_f^2}{{\left(\frac{D^2}{4}{n}_1\right(0\left)\sqrt{A_1}\right)}^2-{\left(\frac{{\mathrm{NA}}_f^2}{n_2\left(0\right)\sqrt{A_2}}\right)}^2}}}{\sqrt{A_2}}---\left(14\right)$

其中，z₁为第一自聚焦透镜元110的厚度，z₂为第二自聚焦透镜元120的厚度，z_Δ为第一、第二自聚焦透镜元110、120之间的距离，n₁(0)为第一自聚焦透镜元110的中心折射率，n₂(0)为第二自聚焦透镜元120的中心折射率。A₁为第一自聚焦透镜元110的聚焦常数，A₂为第二自聚焦透镜元120的聚焦常数，D为第一、第二自聚焦透镜元110、120的直径，两个自聚焦透镜元的直径相等。

当第一自聚焦透镜元110和第二自聚焦透镜元120的聚焦常数A₁、A₂，中心折射率n₁(0)、n₂(0)，直径D、耦合光纤30的数值孔径NA_f确定，则每层自聚焦透镜元的厚度和间距就可以确定，且可以确保很好的耦合效率。系统的厚度可根据实际情况来确定。

自聚焦透镜的折射率沿半径方向按一定规律渐变，折射率的渐变分布使它具有良好的聚光能力；通信中如果要提高光纤的耦合效率，需要光束同时拥有较小的束腰半径和发散角，自聚焦透镜可以减小束腰宽度，而且，与一般的透镜相比，它的束腰半径在减小时所引起的发散角的增大程度要小得多，因此，使用自聚焦透镜，系统耦合效率更高。其次，自聚焦透镜阵列(这里包括第一、第二自聚焦透镜阵列11、12)由多个小透镜组成，分别对信号光进行接收，孔径小能提高耦合效率，抑制湍流的能力更强，所以整个双层自聚焦透镜阵列10同时拥有小孔径和大面积的优势，而且可以同时校正球差和像散，一般透镜或透镜阵列无法达到此效果。

经过计算及仿真，可以得到如图4所示的耦合曲线，上方曲线为半径和焦距分别为原半径和焦距三分之一的双层自聚焦透镜阵列10(包括7个小透镜)的耦合曲线，下方是双自聚焦透镜单元(相当于与7个小透镜外切的大圆O’)的耦合曲线。经过分析计算，可得出如下结论，双层自聚焦透镜阵列10既缩小了光斑尺寸也尽量减小了发散角，具有更好的偏移容忍度，在大气湍流中也具有较好的抑制湍流的作用，在传输同样距离的情况下，双自聚焦透镜阵列10的耦合效率下降更缓慢，在长距离传输中表现出了良好的优势。

请参阅图5，本发明第二实施例提供的双层自聚焦透镜阵列20与第一实施例提供的双层自聚焦透镜阵列10相比基本相同，不同之处在于，第一自聚焦透镜元210的入光面2101为球面。

由于自聚焦透镜的平面状的端面所产生的反射光会干扰光源，并且平端面自聚焦透镜会造成一定的球差，从而导致会聚光斑较大，因此，优选地，将端面2101研磨成球面以校正球差，且能减小反射光的干扰，进一步提高耦合效率。

请参阅图6，本发明第三实施例提供的双层自聚焦透镜阵列50与第一实施例提供的双层自聚焦透镜阵列10相比基本相同，不同之处在于，耦合光纤具体包括多条拉锥光纤53。拉锥光纤53和单模光纤相比而言其端面直径变大，因此只需要将拉锥光纤53尽可能覆盖到较多的第二自聚焦透镜元52，例如，两个、三个或者更多的第二自聚焦透镜元52公用一个拉锥光纤53。拉锥光纤53的入光面530紧贴第二自聚焦透镜元52的出光面520。

由拉锥光纤33接收聚焦光斑可以尽量减小合束损耗，进一步提高耦合效率。

以上所述实施例仅表达了本发明的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对本发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。因此，本发明专利的保护范围应以所附权利要求为准。