一种高效并且稳定的模拟吊车、起重机中不可拉伸绳索的方法

1.本发明属于机械工程领域，具体涉及一种高效并且稳定的模拟吊车、起重机中不可拉伸绳索的方法。


背景技术：

2.在起重机和吊车作业中，稳钩控制是一个十分常见业务。人工控制往往非常耗时并且需要驾驶员长时间的训练。现在基于控制算法、强化学习等技术的发展，自动稳钩技术开始发展。而在这些技术中，开销最大的就是正向模拟技术。传统分段线性不可扩展的绳索通常用顶点的笛卡尔坐标和段上的四元数表示。该方法使用了过多的自由度，为了描述一个精确的不可拉伸绳索，需要额外施加三类约束：不可拉伸约束、单位四元数约束以及局部坐标系的轴与绳索对齐的约束。离散后的绳索的每一段都需要施加这三类约束，约束数量巨大。为了满足此类约束，常见的方法有惩罚函数法以及拉格朗日乘子法，都给模拟带来了不必要的数值困难和计算负担。具体的说，惩罚函数法有三大缺点：它不仅会给动力学系统引入额外的数值耗散，而且惩罚函数的权重系数需要手动调节，另外没有精确满足前述的三类约束。拉格朗日乘子法有两大缺点：它不仅会导致一个巨大的系统矩阵大幅度提升求解的开销，而且上述三类约束都是非线性约束，需要多次迭代求解才能精确满足。因此，本发明提供了一种非常高效并且稳定的模拟不可拉伸绳索的方法。


技术实现要素：

3.针对上述问题，本发明提出了一种高效并且稳定的模拟吊车、起重机中绳索的方法，在该方法中，将杆视为刚性段链，将其形状编码为其根顶点的笛卡尔坐标以及每个段上的材料框架的轴角表示。在这种表示下，隐式时间步进的海森矩阵具有特殊的非零排布，利用该特性，可以以近似线性复杂度来求解相关线性方程。此外，本发明还设计了一种预条件，使得计算速度提高了一个或两个数量级。
4.为了实现上述目的，本发明采用的技术方案为：
5.一种高效并且稳定的模拟吊车、起重机中不可拉伸绳索的方法，包括：
6.s1，将不可拉伸绳索离散表示为起始点的笛卡尔坐标以及每一段的轴角表示，得到绳索的自由度与绳索的紧凑表达之间的转换关系；
7.s2，根据绳索的自由度表示建模绳索的动力学方程，使用隐式欧拉对绳索的动力学方程进行时间离散，得到间隔为时间步长δt的时间离散点，每一个离散点对应一帧；
8.s3，将时间离散后的动力学方程转化为优化问题，使用序列二次规划方法求解优化问题，得到每一帧对应的绳索的紧凑表达，实现对不可拉伸绳索的模拟。
9.进一步地，所述的步骤s1具体为：
10.s11，将不可拉伸绳索的起始点的笛卡尔坐标表示为p0＝{p
0，x
，p
0，y
，p
0，z
}，将不可拉伸绳索的第i段的轴角表示为ωi＝{ω
i，0
，ω
i，1
，ω
i，2
}；
11.其中，i＝1，2，...，n-1，n表示绳索的顶点数量，p
0，x
，p
0，y
，p
0，z
分别是起始点p0的x、y、z轴坐标，ω
i，0
，ω
i，1
，ω
i，2
分别是第i段轴角的三个分量；
12.s12，根据轴角计算绳索每一段的四元数表达：
[0013][0014]
其中，qi表示第i段的四元数表达，||.||表示取模，ωi表示第i段的轴角表示；
[0015]
s13，根据轴角计算局部坐标系：
[0016]
mi＝exp ωi[0017]
其中，mi表示第i段的局部坐标系；
[0018]
s14，根据起始点的笛卡尔坐标，递推其余顶点的笛卡尔坐标，递推计算公式为：
[0019]
p
i+1
＝pi+lid(mi)
[0020]
其中，pi表示第i-1个顶点的笛卡尔坐标，li表示第i段的长度，d(.)表示抽取局部坐标系中的第三个轴；
[0021]
s15，将绳索的自由度表示为：
[0022][0023][0024]
p0＝{p
0，x
，p
0，y
，p
0，z
}
[0025]
ω＝(ω1，ω2，...，ωi，...，ω
n-1
)
[0026]
ωi＝{ω
i，0
，ω
i，1
，ω
i，2
}
[0027]
其中，x表示绳索的自由度，p表示绳索中各顶点的位置，q表示绳索中各段的四元数表达；t(.)表示坐标转换函数，用于表示绳索的自由度与绳索的紧凑表达之间的转换关系；s表示绳索的紧凑表达，ω表示绳索中各段的轴角集合，上角标t表示转置。
[0028]
进一步地，所述的步骤s3具体为：
[0029]
s31，将时间离散后的动力学方程转化成目标函数为弯曲扭转势能v(q)、平移动能增量t
p
(p)、旋转动能tq(q)和重力势能g(p)的和，并且受到来自于碰撞的不可穿透约束ci(x)≥0的优化问题，表示为：
[0030]
x
t+δt
＝argmine(x)＝v(q)+t
p
(p)+tq(q)+g(p)
[0031]
s.t.ci(x)≥0
[0032]
其中，x
t+δt
表示绳索下一帧的自由度，e(x)表示隐式欧拉转化后的优化目标函数，ci(x)表示点面或者段段之间的距离，x表示绳索的自由度，p表示绳索中各顶点的位置，q表示绳索中各段的四元数表达；
[0033]
s32，将步骤s31中的优化问题转化为以绳索的紧凑表达s替代自由度x的优化问题：
[0034]st+δt
＝argmine(t(s))
[0035]
s.t.ci(t(s))≥0
[0036]
其中，s表示绳索的紧凑表达，t(.)表示坐标转换函数，用于表示绳索的自由度与绳索的紧凑表达之间的转换关系，s
t+δt
表示绳索下一帧的紧凑表达；
[0037]
s33，选取线搜索方法来保证收敛性，所述的线搜索方法的衡量函数φ(.)为：
[0038][0039]
其中，μ表示拉格朗日乘子最大值的倒数，||.||表示取模；
[0040]
s34，使用序列二次规划方法求解优化问题：
[0041][0042][0043][0044][0045]
其中，δsk表示第k次迭代的紧凑表达s的增量，上角标t表示转置，δs表示紧凑表达s的增量，ak表示第k次迭代的系统矩阵，表示对紧凑表达s求导，bk表示第k次迭代的右手项，j(.)表示坐标转换函数t(.)的导数，sk表示第k次迭代的紧凑表达，h表示目标函数e(x)以x为变量的海森矩阵。
[0046]
进一步地，所述的弯曲扭转势能v(q)、平移动能增量t
p
(p)、旋转动能tq(q)和重力势能g(p)的计算公式为：
[0047][0048][0049][0050][0051]
其中，m
p
为集中质量矩阵，p
t
为上一帧的每一个顶点的笛卡尔坐标位置，p为每一个顶点的笛卡尔坐标，δt为时间步长，为上一帧的每一个顶点的速度，j
kk
为转动惯量，li为第i段的长度，bk为常数反对称矩阵，qi表示第i段的四元数表达，表示第i段的四元数表达的时间导数，hi为第i个顶点的质量，g为重力加速度，p
i，y
为第i个顶点的y坐标，k
kk
为单元刚度对角矩阵。
[0052]
进一步地，在步骤s34所述的使用序列二次规划方法求解优化问题时，使用活跃集的方法处理碰撞生成相应的kkt矩阵，并使用舒尔补理论方法进行求解，具体为：
[0053]
首先，根据离散碰撞检测方法得到碰撞对，并生成点面碰撞约束和段段碰撞约束ci，表达式如下：
[0054][0055]
其中，pa为点面碰撞中点的坐标，pi、pj和pk为点面碰撞中三角形面片中三个顶点的坐标。段段碰撞对有两个绳索中的段，其中一段的两个顶点为pi和p
i+1
，另一段的两个顶点为pj和p
j+1
，wi、wj、wk分别表示为pi、pj、pk的重心坐标，δ表示碰撞检测的阈值，n表示碰撞法向；
[0056]
之后，使用活跃集的方法提取ci中的活跃的碰撞约束ca，将步骤s34中的二次规划问题转化为求解如下kkt矩阵：
[0057][0058]
其中，λ表示拉格朗日乘子；
[0059]
使用舒尔补理论方法将kkt矩阵转换为如下方程组：
[0060][0061]
其中，(ak)-1
表示ak的逆。
[0062]
进一步地，使用预条件共轭梯度法对(ak)-1
进行求解，在求解过程中，使用三对角矩阵作为预条件将ak作为左手项进行方程求解，所述的预条件为：
[0063][0064]
其中，p为预条件，diagblk(.)为提取分块对角部分的函数；j
p，s
为绳索中各顶点的位置p对绳索的紧凑表达s的导数，j
q，ω
为绳索中各段的四元数表达q对绳索中各段的轴角ω的导数，h
p
为目标函数e(x)对绳索中各顶点的位置p的导数，hq为目标函数e(x)对绳索中各段的四元数表达q的导数，上角标表示转置。
[0065]
进一步地，所述的预条件中的和两项均能够在线性复杂度下构造，构造方法为：
[0066]
(1)在已知j
q，ω
和hq的情况下，的第(i，j)个分块的计算方法为：
[0067][0068]
其中，blk
i，i
(.)、blk
i，j
(.)、blk
j，j
(.)分别表示提取矩阵中第(i，i)、(i，j)、(j，j)个分块；
[0069]
(2)在已知j
p，s
和h
p
的情况下，的第(i，i)个分块的计算方法为：
[0070][0071]
其中，blk
k，k
(.)表示提取矩阵中第(k，k)个分块，n表示绳索的顶点数量。
[0072]
与现有技术相比，本发明的优势在于：
[0073]
(1)因为本发明采用了紧凑的表达形式，相比于使用传统离散方法避免引入不可拉伸约束、单位四元数约束以及局部坐标系的轴与绳索对齐的约束，从而使得动力学方程的条件数大大降低。
[0074]
(2)因为本发明采用了紧凑的表达形式，相比于传统离散方法下的惩罚函数法，避免引入大权重的惩罚项，降低了模拟的数值耗散，并且能够精确刻画不可拉伸绳索。
[0075]
(3)因为本发明采用了紧凑的表达形式，相比于传统离散方法下的拉格朗日乘子法，避免引入过多的约束项，从而大大简化了最终的kkt矩阵，提高了求解的效率。
[0076]
(4)因为本发明探究了该紧凑表达形式下目标函数海森矩阵的特殊结构并针对性的开发了一个可以线性复杂度构造的、具有三对角结构的预条件，与已有的对角预条件，更好的保留了原矩阵的项，从而能够在计算复杂度上提高一到两个数量级。
附图说明
[0077]
图1为本发明的一个实施例中绳索的离散表达方式示意图。
[0078]
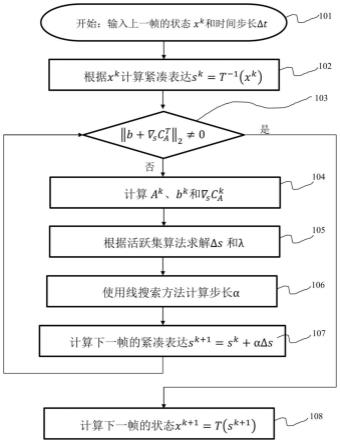
图2为本发明的一个实施例中序列二次规划的算法流程图。
[0079]
图3为本发明的一个实施例中计算得到的结果示意图。
[0080]
图4为本发明的另一个实施例中计算得到的结果示意图。
具体实施方式
[0081]
为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图对本发明的具体实施方式做详细的说明。在下面的描述中阐述了很多具体细节以便于充分理解本发明。但是本发明能够以很多不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似改进，因此本发明不受下面公开的具体实施例的限制。本发明各个实施例中的技术特征在没有相互冲突的前提下，均可进行相应组合。
[0082]
在本发明的描述中，需要理解的是，术语“第一”、“第二”仅用于区分描述目的，而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括至少一个该特征。
[0083]
本发明提出的一种高效稳定的模拟不可拉伸绳索的方法，主要包括以下步骤：
[0084]
步骤一，将不可拉伸绳索离散表示为起始点的笛卡尔坐标以及每一段的轴角表示。
[0085]
如图1所示，对于一个由n个顶点(p0，p1，...，p
n-2
，p
n-1
)离散的绳子，共计n-1段，本发明提出的紧凑表达方式为仅仅使用第一个点p0的笛卡尔坐标以及每一段上的轴角表示，通过轴角表示来获得每一段的方向，从而递推得到第2个顶点p1到第n个顶点p
n-1
的笛卡尔
坐标。
[0086]
s11、将起始点表示为pc＝p0＝{p
0，x
，p
0，y
，p
0，z
}，将第i段的轴角表示为ωi＝{ω
i，0
，ω
i，1
，ω
i，2
}，i＝1，2，
…
，n-1，p
0，x
，p
0，y
，p
0，z
分别是点p0的x、y、z轴坐标，ω
i，0
，ω
i，1
，ω
i，2
分别是第i段轴角的三个分量。
[0087]
s12、根据轴角计算每一段的四元数表达：
[0088][0089]
其中，qi表示第i段的四元数表达，||.||表示取模，ωi表示第i段的轴角表示；
[0090]
s13、根据轴角计算局部坐标系；
[0091]
mi＝exp ωi[0092]
其中，mi表示第i段的局部坐标系；
[0093]
s14、根据起始点的笛卡尔坐标，递推其余顶点的笛卡尔坐标，递推计算公式为：
[0094]
p
i+1
＝pi+lid(mi)
[0095]
其中，pi表示第i-1个顶点的笛卡尔坐标，li表示第i段的长度，d(.)表示抽取局部坐标系中的第三个轴；
[0096]
s15、将绳索的自由度表示为：
[0097][0098][0099]
p0＝{p
0，x
，p
0，y
，p
0，z
}
[0100]
ω＝(ω1，ω2，...，ωi，...，ω
n-1
)
[0101]
ωi＝{ω
i，0
，ω
i，1
，ω
i，2
}
[0102]
其中，x表示绳索的自由度，p表示绳索中各顶点的位置，q表示绳索中各段的四元数表达，t(.)表示坐标转换函数，s表示绳索的紧凑表达式，ω表示绳索中各段的轴角集合，上角标t表示转置。
[0103]
步骤二，根据绳索的自由度表示建模绳索的动力学方程，使用隐式欧拉对绳索的动力学方程进行时间离散，得到间隔为时间步长δt的时间离散点，每一个离散点对应一帧；将时间离散后的动力学方程转化为优化问题，使用序列二次规划方法求解优化问题，得到每一帧对应的绳索的紧凑表达，实现对不可拉伸绳索的模拟。
[0104]
本步骤中，具体实现方法为：
[0105]
s21、依据基尔霍夫理论建模以为自由度的绳索的动力学方程，并转化为目标函数为弯曲扭转势能v(q)、平移动能增量t
p
(p)、旋转动能tq(q)和重力势能g(p)的和并且受到来自于碰撞的不可穿透约束ci(x)≥0的优化问题：
[0106]
x
t+δt
＝argmine(x)＝v(q)+t
p
(p)+tq(q)+g(p)
[0107]
s.t.ci(x)≥0
[0108]
其中，x
t+δt
表示绳索下一帧的自由度，e(x)表示隐式欧拉转化后的优化目标函数，ci(x)表示点面或者段段之间的距离，x表示绳索的自由度，p表示绳索中各顶点的位置，q表示绳索中各段的四元数表达。
[0109]
上述平移动能增量计算公式为：
[0110][0111]
其中，m
p
为集中质量矩阵，p
t
为上一帧的每一个顶点的笛卡尔坐标位置，p为每一个顶点的笛卡尔坐标，δt为时间步长，为上一帧的每一个顶点的速度。
[0112]
旋转动能计算公式为：
[0113][0114]
其中，f
kk
为转动惯量，为四元数的时间导数，li为第i段的长度，bk为常数反对称矩阵，qi表示第i段的四元数，表示第i段的四元数的时间导数。
[0115]
弯曲扭转势能计算公式为：
[0116][0117]
其中，表示绳索的自然曲率，k
kk
为单元刚度对角矩阵，该矩阵的项为：k
11
＝k
22
＝eπr2/4，k
33
＝gπr2/2。其中e和g为杨氏模量和剪切模量，r为绳索的横截面半径；bk为常数反对称矩阵，具体形式如下：
[0118][0119]
重力势能的计算公式为：
[0120][0121]
其中，hi为第i个顶点的质量，g为重力加速度(默认重力施加在方向上)，p
i，y
为第i个顶点的y坐标。
[0122]
s22，将步骤s21中的优化问题转化为以绳索的紧凑表达s替代自由度x的优化问题：
[0123]st+δt
＝argmine(t(s))
[0124]
s.t.ci(t(s))≥0
[0125]
其中，s表示绳索的紧凑表达，t(.)表示坐标转换函数，用于表示绳索的自由度与绳索的紧凑表达之间的转换关系，s
t+δt
表示绳索下一帧的紧凑表达；
[0126]
s23，选取线搜索方法来保证收敛性，所述的线搜索方法的衡量函数φ(.)为：
[0127][0128]
其中，μ表示拉格朗日乘子最大值的倒数，||.||表示取模；本实施例中，通过线搜索方法计算搜索步长α；
[0129]
s24，使用序列二次规划方法求解优化问题：
[0130][0131][0132]
其中，δsk表示第k次迭代的紧凑表达s的增量，上角标t表示转置，δs表示紧凑表达s的增量，ak表示第k次迭代的系统矩阵，表示对紧凑表达s求导，bk表示第k次迭代的右手项；系统矩阵ak和右手项bk的计算公式为：
[0133][0134][0135]
其中，j(.)表示坐标转换函数t(.)的导数，sk表示第k次迭代的紧凑表达，h表示目标函数e(x)以x为变量的海森矩阵。
[0136]
在本发明的一项具体实施中，求解上述步骤s24中所述的二次规划问题时，使用活跃集的方法处理碰撞生成相应的kkt矩阵，并使用舒尔补理论(schur complement)方法进行求解。
[0137]
具体的实现步骤为：
[0138]
s241，根据离散碰撞检测方法得到碰撞对，并生成点面碰撞约束和段段碰撞约束ci如下：
[0139][0140]
其中，pa为点面碰撞中点的坐标，pi、pj和pk为点面碰撞中三角形面片中三个顶点的坐标。
[0141]
段段碰撞对有两个绳索中的段，其中一段的两个顶点为pi和p
i+1
，另一段的两个顶点为pj和p
j+1
，wi、wj、wk分别表示为pi、pj、pk的重心坐标，δ表示碰撞检测的阈值，n表示碰撞法向；
[0142]
s242，使用活跃集的方法提取ci中的活跃的碰撞约束ca，
[0143]
s243，将求解s24中的二次规划问题转化为求解如下kkt矩阵：
[0144][0145]
其中，为活跃的碰撞约束，λ表示拉格朗日乘子；
[0146]
s244，求解该矩阵使用舒尔补理论(schur complement)方法进行求解，也就是转换为求解如下两条方程组：
[0147]
[0148]
其中，λ表示拉格朗日乘子，(ak)-1
表示ak的逆，具体实现是并不会直接求解矩阵的逆，而是将ak作为左手项进行方程求解，因此。求解该方程组时，开销最大的步骤就是求解以ak为左手项的方程，一共需要求解约束数量+2次方程。
[0149]
为了加速该求解，本发明使用预条件共轭梯度法(pcg)求解，具体的，针对ak，使用一种特殊三对角矩阵作为预条件，加速以ak为左手项的方程的求解，过程如下：
[0150]
首先，根据步骤s24可知，a＝j
t
hj，矩阵h具有如下结构：
[0151][0152][0153][0154]
其中，h
p
为目标函数e(x)对绳索中各顶点的位置p的导数，hq为目标函数e(x)对绳索中各段的四元数表达q的导数，kq表示弯曲扭转势能对q的海森矩阵，mq表示广义的旋转惯量矩阵。
[0155]
矩阵j具有如下结构：
[0156][0157]
其中，j
q，s
为绳索中各段的四元数表达q对绳索的紧凑表达s的导数，该矩阵为分块对角矩阵，具体表示声对角矩阵，具体表示声为0，为分块对角矩阵；j
p，s
为绳索中各顶点的位置p对绳索的紧凑表达s的导数，该矩阵为下三角矩阵。
[0158]
之后，基于上述特殊结构，系统矩阵a可以简化为：
[0159][0160]
则预条件为：
[0161][0162]
其中，p为预条件，为提取中的分块对角部分，表示绳索中各段的四元数表达q对绳索中各段的轴角ω的导数；
[0163]
上述预条件中的和都可以在线性复杂度下构造，因此p可以在线性复杂度下构造。
[0164]
在本发明的一项具体实施中，线性构造和的方法为：
[0165]
在已知j
q，ω
和hq的情况下，的第(i，j)个分块的计算方法为：
cpu，32gb内存的台式机上得到了50fps的帧率。
[0185]
以上列举的仅是本发明的具体实施例。显然，本发明不限于以上实施例，还可以有许多变形。本领域的普通技术人员能从本发明公开的内容直接导出或联想到的所有变形，均应认为是本发明的保护范围。