基于到达时间的多目标定位外部逼近近似凸优化算法的制作方法

本发明属于基于无线信号定位
技术领域：
，特别涉及一种多目标定位问题的凸优化算法，适用于基于toa的多目标定位问题。
背景技术：
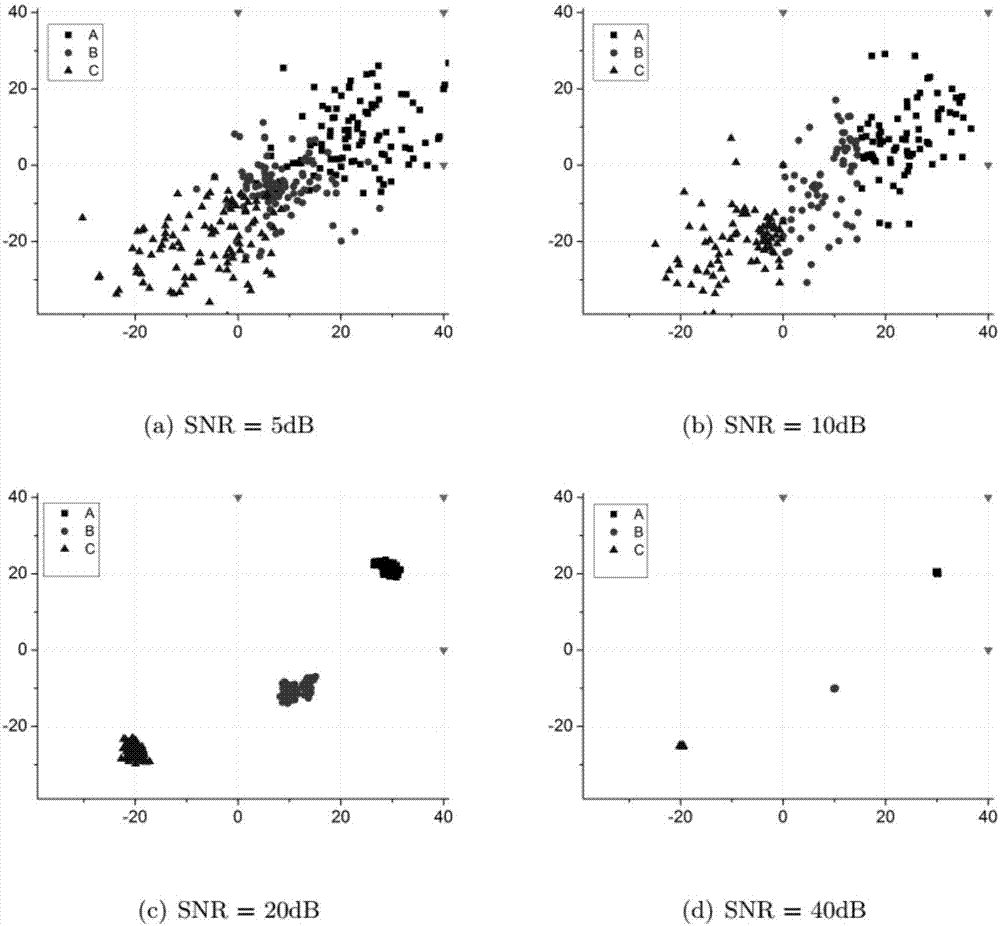
：无线定位技术，最早用于二战时期对舰艇和战斗机等军事目标的定位问题。随着科技的发展，无线定位技术越来越多的在工业、民用和国防等领域得到了广泛的应用。比如紧急救援响应，危险物品追踪，手机定位，过程控制。通过数学方法来改进无线定位算法的估计速度和精度一直是相关科技人员关心的问题。得益于凸优化算法的发展，高效的凸优化松弛技术能应用于目标定位问题。随着大数据、移动互联网和物联网等技术的快速发展，多目标定位问题已成为一个无线定位领域的研究热点。目前的主要研究关注于使用最新的凸优化算法去完善单目标定位问题，主要使用了半正定松弛，二次锥松弛和分枝界限法等方法来解决单目标定位问题。其中为了提高计算效率，一阶加速算法，拟牛顿法和内点法等高收敛速度的算法也应用在计算以上的松弛后的问题中。特别地，对于多目标定位问题，因为基站不能识别信号源于哪一个目标，因此该问题是一个np-hard问题，现有多目标定位算法只能在合理布置基站，然后目标分布在特定范围的前提下，选择合适的起始估计点的条件下才能得到一个全局最优解。否则，只能确保收敛到一个局部最优解。并且为了解决np-hard问题，计算复杂度随着目标数量的增加而呈现出指数级的增加，并且容易陷于局部最优解。因此设计一种能提高对基站和目标位置鲁棒性、高收敛速度和收敛至全域最优的算法具有很大的实际应用前景。技术实现要素：针对上述现有技术的不足，本发明的目的在于提出一种基于到达时间(toa)的多目标定位外部逼近近似凸优化算法(oaa)，该方法基于外部近似逼近凸优化算法最突出的优势在于，利用外部近似逼近算法，对基站的布局和目标所在区域没有现有方法如此复杂的要求，并且能够确保收敛到全域最优解，并且不需要初始估计点。本发明是这样实现的：实现本发明的技术思路是首先构造原始问题模型(1)，然后使用松弛方法将原问题松弛为一个混合整数凸优化问题模型(2)，并针对半正定矩阵构建新的合适的约束，然后使用外部逼近近似算法子模型(3)和连续凸优化问题模型(4)，使用oaa算法求得待定位的各个目标的坐标值。本发明更具体的步骤如下：基于到达时间的多目标定位(timeofarrivalbasedmultiplesourcelocalizationtoa-msl)外部逼近近似凸优化算法(outerapproximalapproachalgorithmoaa)，，包括通过半正定松弛，二次锥松弛、泰勒松弛和添加sdp约束条件后，根据最大似然估计(mle)模型得到一个混合整数凸优化问题，根据外部逼近近似算法得到精确的多目标坐标。具体包括以下步骤：a)通过toa定义，使用最大似然估计构造了一个混合整数、非凸的原始问题模型(1)；b)通过采用半正定松弛、泰勒松弛和二次锥松弛等松弛方法以及添加sdp约束条件，将原问题松弛为一个混合整数凸优化问题模型(2)；c)通过解外部逼近近似算法子模型(3)得到一个整数部分的解p，对应的最优函数值作为整个算法的下界(lb)；d)固定整数解部分，b)对应的混合整数凸优化问题模型(2)变为一个连续凸优化问题模型(4)，通过解该连续凸优化问题模型(4)得到连续部分解，及对应的函数值,对应函数值中的最小值为整个算法的上界(ub)；e)判断连续凸优化问题模型(4)得到的解是否是原问题的最优解：ⅰ.ifub>lb+constant，d)中的连续解以及与他相对应的整数解不是原问题的最优解，迭代升级b)中的外部逼近近似算法子模型(3)的约束条件，确保已经出现过的整数解不会再次出现，继续执行b)-d)直至得到最优解或者迭代次数超过预设的上限。ⅱ.ifub<＝lb+constant,d)中的连续解以及与他相对应的整数解为原问题的最优解，停止程序。更进一步的方案是：所述步骤a)包括：ⅰ.toa定义,假设有k个目标待定位x其对应一个l×k矩阵，m个基站s对应一个l×m矩阵，其中基站的位置矩阵s已知，到达时间对应的k×m矩阵d已知，目标的位置矩阵x未知。根据toa定义可知，第k个目标到第i个基站的到达时间如下所示：其中，最后一项为噪音，不失一般性的，我们假设每个噪声都服从高斯分布，并且独立同分布。多目标定位中，假设对于每一个基站不能识别他获得的信号来自于哪一个目标(表示为)，为了识别每一个目标，我们为每一个基站引入一个了置换矩阵(permutationmatrix)以识别每一个目标，方法如下(对于第i个基站，识别来自第k个目标的toa值)：ⅱ.通过最大似然估计，去最小化噪声的绝对值，基于此我们构造了如下多目标定位模型(1)：zk，i≥0，pi∈π，原始问题模型(1)其中，pi表示第i个基站对应的置换矩阵；为第i个基站接收的toa数据；zk,i表示第k个目标与第i个基站的实际toa数据与估计数据的差异的平方；为待计算的第k个目标与第i个基站的真实toa值；第二个约束是toa的物理定义。显而易见的，该问题是一个混合整数非凸问题，现有算法很难确保收敛到全局最优解。更进一步的方案是：所述步骤b)包括：ⅰ.根据所述toa数据和基站的位置信息来计算多个目标的位置；ⅱ.对原始问题进行包括但不限于半正定松弛、二次锥松弛、泰勒松弛和添加sdp约束条件以使得原问题变为凸问题以及降低计算复杂度。更进一步的方案是：所述步骤c)包括：ⅰ.松弛掉sdp约束的半正定的约束条件，得到外部逼近近似算法子模型(3)；ⅱ.外部逼近近似算法子模型(3)是一个混合整数-二次锥凸优化问题；ⅲ.松弛后的外部逼近近似算法子模型(3)，可以使用包括但不限于分支定界算法、内点法、固定步长梯度下降法、变步长梯度下降法和牛顿法来得到子问题的最优解和最优函数值；ⅳ.保存最优解的整数部分，最优函数值被定义为原问题的下界lb，进入步骤c)。更进一步的方案是：所述步骤d)包括：ⅰ.固定整数部分后，原混合整数凸优化问题模型(2)变为了一个连续的带有半正定约束和二次锥约束的连续可微分凸优化问题；ⅱ.该问题可以使用包括但不限于内点法、梯度下降法(固定步长，变化步长)和牛顿法等成熟的凸优化算法来得到该子问题的最优解和最优函数值；ⅲ.最优函数值被记为原问题的上界(ub)。更进一步的方案是：所述步骤e)包括：确保整数解不重复的方法包括但不限于：ⅰ.计算d)中连续凸优化问题模型(4)的对偶问题，得到位置变量x的松弛变量x对应的对偶最优解x_dual和真实到达时间d对应的松弛变量d的对偶最优解d_dual,在b)的子问题中添加约<x,x_dual>>＝0(克罗内克积)；<d,d_dual>>＝0.ⅱ.直接在b)的外部逼近近似算法子模型(3)中添加约束<p,p><＝m×k-1.(p为b)步中得到的整数解)更进一步的方案是：构建最大似然估计(mle)模型，包括：ⅰ.建立噪声的概率密度函数(包括但不限于服从高斯分布)；ⅱ.计算实际到达时间表示为d0+ε；ⅲ.目标函数为噪声的平方和最小化；ⅳ.考虑的噪声信噪比(snr)主要范围为0-100db。更进一步的方案是：步骤b)中松弛步骤，半正定松弛和二次锥松弛，得到以下松弛后的最大似然估计问题，即混合整数凸优化问题模型(2)其中第一个约束是二次锥松弛，第二个、第三个、第四个和第五个约束条件是半正定松弛，通过半正定松弛和二次锥松弛后得了一个混合整数-半正定-二次锥的凸优化问题模型(2)。更进一步的方案是：泰勒松弛具体步骤如下：通过对原始问题模型(1)中第二个约束条件的进行泰勒一阶松弛、二阶松弛或者高阶松弛，从而得到一个松弛的一阶、二阶或者高阶不等式，从而将问题转化一个混合整数-二次锥的凸优化问题。更进一步的方案是：添加新的松弛后的半正定矩阵(sdp)约束条件，具体为：对半正定松弛后的半正定矩阵d添加约束条件，以保证半正定矩阵中对角元元素dik,k数值尽可能接近(dik,l+1)2，从而确保半正定松弛与原问题等价，使用的方法包括但不限于添加如下约束条件：更进一步的方案是：外部逼近近似算法子模型(3)，其模型包含但不限于如下所示特征：<di，ddual{iternum}i>≥0<xk，xdual{iternum}k>≥0外部逼近近似算法子模型(3i)zk，i≥0，pi∈π，外部逼近近似算法子模型(3ii)更进一步的方案是：连续凸优化问题模型(4)，其模型包含但不限于如下所示特征：连续凸优化问题模型(4)该模型是一个连续-半正定-二次锥凸优化问题，可以使用凸优化算法得到最优解，其中第一个约束条件表示将得到的整数解带入我们的toa数据，从而消掉0-1整数变量。更进一步的方案是：d_dual真实到达时间d对应的半正定松弛变量d的对偶最优解d_dual,和目标位置未知变量x对应的半正定松弛变量x的对偶最优解x_dual，可通过计算具有以下特征的凸优化问题得到：松弛问题对应的对偶问题模型其中第二个和第三约束分布代表了d_dual和x_dual。本发明公开的基于到达时间(toa)的多目标定位外部逼近近似凸优化算法(oaa)，在有限次的迭代后就能得到一个全局最优解，仿真结果表明在大规模多目标定位问题中，该方法仍能在很短的时间内得到全局最优解，在信噪比高于30db时，该方法能达到cramér-rao下界(crlb)。该方法可应用于手机定位，救援定位，雷达不明飞行物定位等领域中。附图说明图1为本发明流程示意图；图2为本发明实施例1计算的目标位置散点图；图3为本发明实施例2计算的目标位置散点图。具体实施方式下面结合具体实施方式对本发明作进一步的说明。如附图1所示，一种基于到达时间(toa)的多目标定位外部逼近近似凸优化算法(oaa)，包括通过半正定松弛，二次锥松弛、泰勒松弛和添加sdp约束条件后，根据最大似然估计(mle)模型得到一个混合整数凸优化问题，根据外部逼近近似算法得到精确的多目标坐标。具体包括以下步骤：a)通过toa定义，使用最大似然估计构造了一个混合整数、非凸的原始问题模型(1)；b)通过采用半正定松弛、泰勒松弛和二次锥松弛等松弛方法以及添加sdp约束条件，将原问题松弛为一个混合整数凸优化问题模型(2)；c)通过解外部逼近近似算法子模型(3)得到一个整数部分的解p，对应的最优函数值作为整个算法的下界(lb)；d)固定整数解部分，b)对应的混合整数凸优化问题模型(2)变为一个连续凸优化问题模型(4)，通过解该连续凸优化问题模型(4)得到连续部分解，及对应的函数值,对应函数值中的最小值为整个算法的上界(ub)；e)判断连续凸优化问题模型(4)得到的解是否是原问题的最优解：ⅰ.ifub>lb+constant，d)中的连续解以及与他相对应的整数解不是原问题的最优解，迭代升级b)中的外部逼近近似算法子模型(3)的约束条件，确保已经出现过的整数解不会再次出现，继续执行b)-d)直至得到最优解或者迭代次数超过预设的上限。ⅱ.ifub<＝lb+constant,d)中的连续解以及与他相对应的整数解为原问题的最优解，停止程序。更进一步的方案是：所述步骤a)包括：ⅰ.toa定义,假设有k个目标待定位x其对应一个l×k矩阵，m个基站s对应一个l×m矩阵，其中基站的位置矩阵s已知，到达时间对应的k×m矩阵d已知，目标的位置矩阵x未知。根据toa定义可知，第k个目标到第i个基站的到达时间如下所示：其中，最后一项为噪音，不失一般性的，我们假设每个噪声都服从高斯分布，并且独立同分布。多目标定位中，假设对于每一个基站不能识别他获得的信号来自于哪一个目标(表示为)，为了识别每一个目标，我们为每一个基站引入一个了置换矩阵(permutationmatrix)以识别每一个目标，方法如下(对于第i个基站，识别来自第k个目标的toa值)：ⅱ.通过最大似然估计，去最小化噪声的绝对值，基于此我们构造了如下多目标定位模型(1)：zk，i≥0，pi∈π，原始问题模型(1)其中，pi表示第i个基站对应的置换矩阵；为第i个基站接收的toa数据；zk,i表示第k个目标与第i个基站的实际toa数据与估计数据的差异的平方；为待计算的第k个目标与第i个基站的真实toa值；第二个约束是toa的物理定义。显而易见的，该问题是一个混合整数非凸问题，现有定位算法很难得到全局最优解。更进一步的方案是：所述步骤b)包括：ⅰ.根据所述toa数据和基站的位置信息来计算多个目标的位置；ⅱ.对原始问题进行包括但不限于半正定松弛、二次锥松弛、泰勒松弛和添加sdp约束条件以使得原问题变为凸问题以及降低计算复杂度。更进一步的方案是：所述步骤c)包括：ⅰ.松弛掉sdp约束的半正定的约束条件，得到外部逼近近似算法子模型(3)；ⅱ.外部逼近近似算法子模型(3)是一个混合整数-二次锥凸优化问题；ⅲ.松弛后的外部逼近近似算法子模型(3)，可以使用包括但不限于分支定界算法、内点法、固定步长梯度下降法、变步长梯度下降法和牛顿法来得到子问题的最优解和最优函数值；ⅳ.保存最优解的整数部分，最优函数值被定义为原问题的下界lb，进入步骤c)。更进一步的方案是：所述步骤d)包括：ⅰ.固定整数部分后，原混合整数凸优化问题模型(2)变为了一个连续的带有半正定约束和二次锥约束的连续可微分凸优化问题；ⅱ.该问题可以使用包括但不限于内点法、梯度下降法(固定步长，变化步长)和牛顿法等成熟的凸优化算法来得到该子问题的最优解和最优函数值；ⅲ.最优函数值被记为原问题的上界(ub)。更进一步的方案是：所述步骤e)包括：确保整数解不重复的方法包括但不限于：ⅰ.计算d)中连续凸优化问题模型(4)的对偶问题，得到位置变量x的松弛变量x对应的对偶最优解x_dual和真实到达时间d对应的松弛变量d的对偶最优解d_dual,在b)的子问题中添加约<x,x_dual>>＝0(克罗内克积)；<d,d_dual>>＝0.ⅱ.直接在b)的外部逼近近似算法子模型(3)中添加约束<p,p><＝m×k-1.(p为b)步中得到的整数解)更进一步的方案是：构建最大似然估计(mle)模型，包括：ⅰ.建立噪声的概率密度函数(包括但不限于服从高斯分布)；ⅱ.计算实际到达时间表示为d0+ε；ⅲ.目标函数为噪声的平方和最小化；ⅳ.考虑的噪声信噪比(snr)主要范围为0-100db。更进一步的方案是：步骤b)中松弛步骤，半正定松弛和二次锥松弛，得到以下松弛后的最大似然估计问题，即混合整数凸优化问题模型(2)其中第一个约束是二次锥松弛，第二个、第三个、第四个和第五个约束条件是半正定松弛，通过半正定松弛和二次锥松弛后得了一个混合整数-半正定-二次锥的凸优化问题模型(2)。更进一步的方案是：泰勒松弛具体步骤如下：通过对原始问题模型(1)中第二个约束条件的进行泰勒一阶松弛、二阶松弛或者高阶松弛，从而得到一个松弛的一阶、二阶或者高阶不等式，从而将问题转化一个混合整数-二次锥的凸优化问题。更进一步的方案是：添加新的松弛后的半正定矩阵(sdp)约束条件，具体为：对半正定松弛后的半正定矩阵d添加约束条件，以保证半正定矩阵中对角元元素dik,k数值尽可能接近(dik,l+1)2，从而确保半正定松弛与原问题等价，使用的方法包括但不限于添加约束条件：更进一步的方案是：外部逼近近似算法子模型(3)，其模型包含但不限于如下所示特征：<di，ddual{iternum}i>≥0<xk，xdual{iternum}k>≥0外部逼近近似算法子模型(3i)zk，i≥0，pi∈π，外部逼近近似算法子模型(3ii)更进一步的方案是：连续凸优化问题模型(4)，其模型包含但不限于如下所示特征：连续凸优化问题模型(4)该模型是一个连续-半正定-二次锥凸优化问题，可以使用凸优化算法得到最优解，其中第一个约束条件表示将得到的整数解带入我们的toa数据，从而消掉0-1整数变量。更进一步的方案是：d_dual真实到达时间d对应的半正定松弛变量d的对偶最优解d_dual,和目标位置未知变量x对应的半正定松弛变量x的对偶最优解x_dual，可通过计算具有以下特征的凸优化问题得到：松弛问题对应的对偶问题模型其中第二个和第三约束分布代表了d_dual和x_dual。下面根据实际情况举出两个更具体的实施例进行说明。实施例1基站：s＝4040-40-40400-40040-4040-40040040待定位的目标：x＝10-2030-10-2520100次蒙特卡洛模拟后，计算的目标位置散点图如附图2所示，图2示出了3个目标8个基站的门特卡罗模拟结果图。实施例2基站：s＝4040-40-4040-4040-40待定位的目标：x＝-20020-20020-20020202020000-20-20-20信噪比snr(db)10203040100次蒙特卡洛模拟后，计算的目标位置散点图如附图3所示，图3示出了9个目标4个基站的门特卡罗模拟结果。表1多目标(9个)定位精度与计算复杂度所有数值实验都是由笔记本电脑完成，由附图2、3可知本专利所描述的算法能解决toa-msl定位问题，在信噪比大于等于20db时，能得到不错的数值结果。表1表明，使用本专利所描述的算法解决多目标问题仅需要不到9秒钟，大大低于已知的多目标定位算法，在噪音较小时能接近crlb精度。尽管这里参照本发明的解释性实施例对本发明进行了描述，上述实施例仅为本发明较佳的实施方式，本发明的实施方式并不受上述实施例的限制，应该理解，本领域技术人员可以设计出很多其他的修改和实施方式，这些修改和实施方式将落在本申请公开的原则范围和精神之内。当前第1页12