一种变应力场中非常规储层气-水相渗曲线计算方法与流程

本发明涉及非常规油气藏开发领域，尤其是一种变应力场中非常规储层气-水相渗曲线计算方法。
背景技术：
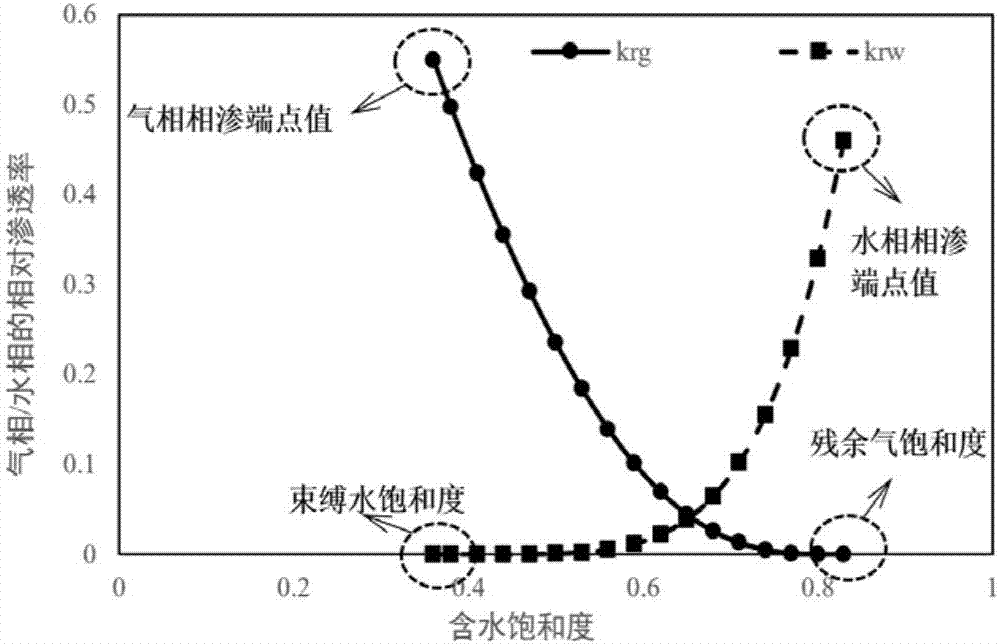
：非常规储层在油气开发领域通常包括致密储层、煤层、页岩储层等多种储层类型，以上储层的特点之一是具有较为显著的应力敏感性。非常规气藏开发过程中，地层压力不断变化，由此所形成的变应力场会导致储层微观孔喉结构发生改变。当储层中同时存在气-水两相流体时，孔喉结构的变化会改变气-水两相的渗流特征，在宏观尺度下表现为气-水相对渗透率特征的变化，进而对非常规气井的生产造成影响。而相渗曲线(又可称为相对渗透率曲线)作为表征气-水两相渗流特征的基础资料，在非常规气藏开发过程中发挥着关键的作用。因此，对于非常规储层，快速准确的获取变应力场中任意应力条件下的相对渗透率曲线，具有十分重要的意义。但是，现有的大部分相对渗透率曲线测试手段或计算方法仅能获得恒定应力条件下的相对渗透率曲线。而多应力条件下相渗曲线的获取则主要依赖于进行不同围压下的岩心驱替实验。该类实验的局限性在于受实验条件及成本的限制，通常仅能获得3～6个压力值所对应的相渗曲线，难以形成完整的定量数学模型，无法获得任意应力条件所对应的相对渗透率曲线，从而难以为非常规气藏的开发提供足够的基础资料。一些基于分形的应力敏感相对渗透率曲线计算方法虽然可以建立相对渗透率与应力之间的关系，但是利用该类方法在计算过程中需要使用较为准确的气井含水率等生产数据。因此，对于未开发的储层，由于尚未进行生产，通常不具备含水率等生产数据，无法使用基于分形的应力敏感相对渗透率曲线计算方法获得变应力场中的非常规储层相渗曲线；另一方面，即使是已开发的非常规储层，由于现场工艺措施及成本的限制，大部分气井也并未记录生产含水率数据，从而限制了该类方法的应用效果。因此，建立一种受实验条件及次数的限制较小，同时不依赖于油田现场实际含水率数据的变应力场中非常规储层气-水相渗曲线快速准确的确定方法显得尤为关键。技术实现要素：本发明要解决的技术问题是：为了克服现有技术中之不足，本发明提供一种变应力场中非常规储层气-水相渗曲线计算方法，解决现有的相对渗透率测试手段及计算模型无法快速准确得获取变应力场中任意应力条件下的非常规储层气-水相对渗透率曲线的问题，从而达到有效计算变应力场中非常规储层气-水相对渗透率曲线的目的。本发明解决其技术问题所采用的技术方案是：一种变应力场中非常规储层气-水相渗曲线计算方法，包括以下步骤：(a)、首先利用实验方法测定5个以上不同应力条件(需包含原始地层压力所对应的应力条件)下的孔隙度及相渗曲线各端点值，并将实验室应力条件折算为所对应的地层压力；(b)、基于原始地层压力所对应的应力条件下的实验结果，拟合以下关系式获得毛管分布指数λ及毛管弯曲系数η；其中，krgi为原始地层压力所对应的应力条件下的气相相对渗透率；krgendi为原始地层压力下的气相相渗端点值；Sw为含水饱和度；Swci为原始地层压力下的束缚水饱和度；Sgri为原始地层压力下的残余气饱和度；λ为毛管分布指数；η为毛管弯曲系数；krwi为原始地层压力所对应的应力条件下的水相相对渗透率；krwendi为原始地层压力下的水相相渗端点值；(c)、基于不同应力条件下的实验数据，拟合孔隙度与地层压力变化的关系得到孔隙度应力敏感系数γ；并基于实验结果，分别根据以下关系式拟合获得相渗曲线各端点值与应力之间的定量表征系数C、D、E、F：利用所获得的相渗曲线各端点值与应力之间的定量表征系数，代入以下关系式，从而构建相渗曲线端点值随应力场的动态变化模型：其中，φ为指定应力条件下的储层孔隙度；φi为原始地层压力所对应的应力条件下的储层孔隙度；krgend-test、krwend-test、Swc-test、Sgr-test分别为实验压力下的气相相渗端点值、水相相渗端点值、束缚水饱和度、残余气饱和度测试结果；krgendi、krwendi、Swci、Sgri分别为原始地层压力所对应的应力条件下的气相相渗端点值、水相相渗端点值、束缚水饱和度、残余气饱和度；krgend、krwend、Swc、Sgr分别为指定地层压力条件下的气相相渗端点值、水相相渗端点值、束缚水饱和度、残余气饱和度；γ为孔隙度应力敏感系数，单位为MPa-1；C为气相相渗端点值应力敏感系数；D为水相相渗端点值应力敏感系数；E为束缚水饱和度应力敏感系数；F为残余气饱和度应力敏感系数；p为指定地层压力，单位为MPa；pi为原始地层压力，单位为MPa；(d)、利用所构建的相渗曲线端点值随应力场的动态变化模型，进一步建立考虑相渗曲线端点值随应力变化的气-水相对渗透率计算模型，并计算不同应力条件下的气-水两相相对渗透率。(e)、利用计算获得的不同应力条件下的气-水两相相对渗透率结果，绘制变应力场中的气-水相对渗透率曲线。其中，上述步骤(d)包括以下步骤：(d1)、基于孔隙度应力敏感系数γ、气相相渗端点值应力敏感系数C，水相相渗端点值应力敏感系数D，利用下式计算不同压力条件下的气-水相对渗透率端点值；(d2)、基于孔隙度应力敏感系数γ、束缚水饱和度应力敏感系数E及残余气饱和度应力敏感系数F，利用下式计算不同压力条件下的标准化水相饱和度其中，为标准化水相饱和度；(d3)、基于标准化水相饱和度、孔隙度应力敏感系数及相渗曲线各端点值的应力敏感系数，利用下式，计算不同压力及饱和度条件下的气-水相对渗透率。其中，krg为气相相对渗透率；krw为水相相对渗透率。本发明的有益效果是：本发明与多应力场条件下的岩心驱替实验相比，可以突破实验条件和次数的限制，在降低测试成本的基础上获得任意应力条件下的相对渗透率曲线，并形成可直接用于后续计算的数学模型，从而为非常规气田的开发提供更加丰富的气-水相渗资料。而与基于分形理论的相对渗透率计算方法相比，本发明不依赖于含水率等现场生产动态资料，可用于缺乏含水率数据的未开发储层及大部分已开发气井，应用范围更广。附图说明下面结合附图和实施例对本发明进一步说明。图1为本发明流程图；图2为相渗曲线上各端点值示意图；图3为本发明实施例中无因次孔隙度变化曲线图；图4为本发明实施例中气相相渗端点值变化曲线图；图5为本发明实施例中水相相渗端点值变化曲线图；图6为本发明实施例中束缚水饱和度端点值变化曲线图；图7为本发明实施例中残余气饱和度端点值变化曲线图；图8为本发明实施例中不同应力条件下的相对渗透率曲线；图9为本发明实施例中等效地层压力为30.7MPa(原始地层压力)时实验与计算结果的对比图；图10为本发明实施例中等效地层压力为20MPa时实验与计算结果的对比图；图11为本发明实施例中等效地层压力为10MPa时实验与计算结果的对比图。具体实施方式现在结合附图对本发明作进一步详细的说明。这些附图均为简化的示意图，仅以示意方式说明本发明的基本结构，因此其仅显示与本发明有关的构成。如图1所示的本发明的流程图，以某非常规气田数据为例，对利用本发明的方法和现有技术中的岩心驱替实验方法进行对比实验，其中，实验中得到的相对渗透率曲线如图9～11所示。而同样的数据，按照本发明的步骤如下操作：(a)、首先利用实验方法测定包含原始地层压力所对应的应力条件在内的5个不同应力条件下的孔隙度及相渗曲线各端点值，并将实验室应力条件折算为所对应的地层压力(等效地层压力)，结果如表1所示；表1不同等效地层压力条件下的参数情况等效地层压力(MPa)无因次孔隙度气相相渗端点值水相相渗端点值束缚水饱和度残余气饱和度30.710.5530.4610.3620.168250.9890.5190.4520.3890.171200.9790.5020.4360.4260.173150.9690.4660.4310.4390.179100.9610.4560.4210.4660.181其中，无因次孔隙度定义为测试应力下的孔隙度与原始地层压力所对应的应力条件下的孔隙度(原始孔隙度)的比值。相渗曲线端点值包括气相相渗端点值、水相相渗端点值、束缚水饱和度、残余气饱和度，以上各点在相渗曲线上的位置如图2所示。(b)、基于原始地层压力所对应的应力条件下的实验结果，拟合以下关系式获得毛管分布指数λ为3.6，毛管弯曲系数η为2.3；其中，krgi为原始地层压力所对应的应力条件下的气相相对渗透率；krgendi为原始地层压力下的气相相渗端点值；Sw为含水饱和度；Swci为原始地层压力下的束缚水饱和度；Sgri为原始地层压力下的残余气饱和度；λ为毛管分布指数；η为毛管弯曲系数；krwi为原始地层压力所对应的应力条件下的水相相对渗透率；krwendi为原始地层压力下的水相相渗端点值；(c)、基于不同应力条件下的实验数据，拟合孔隙度与地层压力变化的关系得到孔隙度应力敏感系数γ为0.0019MPa-1；并基于实验结果，分别根据以下关系式拟合获得气相相渗端点值应力敏感系数C为5.2，水相相渗端点值应力敏感系数D为2.1，束缚水饱和度应力敏感系数E为7.5，残余气饱和度应力敏感系数F为1.8：利用所获得的相渗曲线各端点值与应力之间的定量表征系数，代入以下关系式，从而构建相渗曲线端点值随应力场的动态变化模型：(d1)、基于孔隙度应力敏感系数γ、气相相渗端点值应力敏感系数C，水相相渗端点值应力敏感系数D，利用下式计算不同压力条件下的气-水相对渗透率端点值；(d2)、基于孔隙度应力敏感系数γ、束缚水饱和度应力敏感系数E及残余气饱和度应力敏感系数F，利用下式计算不同压力条件下的标准化水相饱和度其中，为标准化水相饱和度；(d3)、基于标准化水相饱和度、孔隙度应力敏感系数及相渗曲线各端点值的应力敏感系数，利用下式，计算不同压力及饱和度条件下的气-水相对渗透率。其中，krg为气相相对渗透率；krw为水相相对渗透率。(e)、利用计算获得的不同应力条件下的气-水两相相对渗透率结果，绘制不同应力条件下(等效地层压力分别为30.7/20/18/10/5MPa)的气-水相对渗透率曲线，如图8所示，在此基础上，将部分应力条件下(等效地层压力分别为30.7/20/10MPa)的计算结果与实际实验测试结果进行对比，结果如图9～11所示。其中，krg为气相相对渗透率；krw为水相相对渗透率；krgi为原始地层压力所对应的应力条件下的气相相对渗透率；krwi为原始地层压力所对应的应力条件下的水相相对渗透率；krgend为当前压力下的气相相渗端点值；krwend为当前压力下的水相相渗端点值；Swc为当前压力下的束缚水饱和度；Sgr为当前压力下的残余气饱和度；krgendi为原始地层压力下的气相相渗端点值；krwendi为原始地层压力下的水相相渗端点值；Swci为原始地层压力下的束缚水饱和度；Sgri为原始地层压力下的残余气饱和度；Sw为含水饱和度；为标准化水相饱和度；λ为毛管分布指数；η为毛管弯曲系数；γ为相渗曲线应力敏感系数，单位为MPa-1；C为气相相渗端点值应力敏感系数；D为水相相渗端点值应力敏感系数；E为束缚水饱和度应力敏感系数；F为残余气饱和度应力敏感系数；P为当前地层压力，单位为MPa；pi为原始地层压力，单位为MPa。按照该方法实现利用孔隙度及相渗曲线端点值与有效应力之间的关系如图3～7所示，得到相应的应力敏感系数，进一步建立考虑相渗曲线端点值随应力变化的气-水相对渗透率计算模型，然后计算不同应力条件下的相对渗透率曲线如图8所示，图9至图11为岩心应力敏感实验测试得到的不同应力条件下的相对渗透率曲线与计算得到的相对渗透率曲线的对比，从对比的情况可以看出，本发明提出的方案与实验结果吻合程度较高，可以用于油田实际相对渗透率的计算。以上述依据本发明的理想实施例为启示，通过上述的说明内容，相关工作人员完全可以在不偏离本项发明技术思想的范围内，进行多样的变更以及修改。本项发明的技术性范围并不局限于说明书上的内容，必须要根据权利要求范围来确定其技术性范围。当前第1页1 2 3