一种阵列误差条件下的互质阵列DOA估计新方法与流程

阵列天线工程化过程中遇到的阵列误差主要包括阵元方向图误差、阵元位置误差、阵元互耦、通道幅相误差及通道频带误差等。其中，方向图误差和频带误差在特定情况下可以等效为通道幅相误差，因此，关于阵列误差的研究主要围绕阵元位置误差、阵元互耦、通道幅相误差展开。阵元位置误差与来波方向相关，通常称之为方向依赖误差；阵元互耦、通道幅相误差则与来波方向无关，称为方向独立误差。

背景技术：

早期的阵列误差校正是通过对阵列流型进行测量、内插、存储来实现的，这些方法实现代价大且效果不理想。20世纪90年代以后，阵列误差校正研究逐步向参数估计方向发展，通过对各种误差进行建模，依据观测数据对误差参数进行估计。参数估计类阵列误差校正方法可以分为两类，有源校正和无源校正(自校正)。有源校正通过在空间设置方位精确已知的辅助信源，依据观测数据对阵列误差进行离线估计。这类算法以辅助信源方位精确已知为前提，校正过程中不需要对辅助信源的来波方向进行估计，运算量较小，但当辅助信源的来波方向存在偏差时，参数估计结果偏差较大。自校正算法依据观测数据对信源的来波方向和误差参数进行联合估计，不需要设置辅助信源，与有源校正相比系统成本较低，且可以进行在线估计，实现实时校正。但是，由于自校正算法涉及参数联合估计，对应的高维非线性优化问题，计算量巨大，且全局最优解获取困难，为自校正算法研究带来巨大挑战。

关于互质阵列的误差校正问题，相关研究十分匮乏，截止目前可以检索到的文献寥寥无几。针对阵元互耦问题，文献[1]对互耦条件下的互质阵列doa估计进行了探索性研究，首先利用接收互耦阻抗方法(receiving-mutual-impedancemethod，rmim)对互质阵列中阵元间的互耦效应进行衡量，再利用混合参数协方差矩阵自适应迭代算法(covariancematrixadaptationevolutionstrategy，cma-es)对到达角及互耦矩阵进行联合估计；文献[2]研究了阵元互耦对三种稀疏阵列doa估计性能的影响，并提出两种互耦补偿方法。一种方法假设互耦效应部分已知，在迭代过程中分别应用稀疏信号重构和cma-es更新互耦矩阵和到达角；另一种方法假设互耦完全未知，利用cma-es对代价函数进行最小化从而实现互耦矩阵、信号源能量、信号到达角的同时估计。上述两篇文献虽实现了互耦条件下互质阵列的doa估计的问题，但cma-es算法运算量大、耗时长，难以实现误差的实时校正。

针对通道幅相误差问题，目前尚无公开发表的关于互质阵列幅相误差校正的研究成果，但文献[3，4]对嵌套阵列的幅相误差校正问题进行了研究，可以为互质阵列提供参考。其中，文献[3]将幅度误差和相位误差分别进行处理，利用嵌套阵列接收数据协方差矩阵的部分toeplitz性对幅度误差进行估计，对于相位误差则不直接估计误差参数而是通过构建稀疏总体最小二乘(sparsetotalleastsquares，stls)问题直接对信源到达角进行估计。文献[4]在文献[3]的基础上，分析了算法的鲁棒性，并将校正算法扩展到任意非均匀线阵。

针对阵元位置误差问题，文献[5]分析了阵元位置扰动对虚拟阵列基础上的互质阵列doa估计算法的影响，并提出一种稀疏重构类迭代算法实现了doa和阵元位置误差的联合估计。文献[6]利用一阶泰勒级数展开对虚拟阵列的阵列流型进行估计，构建“双仿射”模型，并在此基础之上进行降维处理，将问题转化为线性欠定doa估计问题，最后利用文献[5]中迭代方法进行求解，从虚拟阵列角度解决了均匀线阵及互质阵列的阵元位置误差校正问题。

综合目前的研究成果，互质阵列在拥有分辨能力强、估计精度高、信源处理能力强等优点的同时，其特殊的阵列结构也为误差校正带来困难，主要表现在：

(1)阵元稀疏布置，导致协方差矩阵不再具有toeplitz性，研究成熟的均匀线阵误差校正方法难以适用于互质阵列；

(2)基于互质阵列的doa估计算法扩展测向自由度的关键在于构建了虚拟阵列，而此过程中协方差的运算使得阵列误差成倍增长，增大了误差校正的难度。

鉴于上述难点的存在，互质阵列的误差校正问题尚未得到很好的解决，现有成果普遍存在运算量大、实时性差等问题。因此，本发明针对互质阵列的阵列误差校正问题展开研究。

技术实现要素：

1)提出了阵列误差存在时互质阵列的一般信号模型，该模型能够将误差参数分离出来，便于进行后续处理，对应说明书具体实施方式(1)中的内容，在sbac算法[7]中一般模型的基础上针对互质阵列的特点进行了扩展。

2)提出了基于bessel先验的稀疏贝叶斯模型进行阵列误差条件下的互质阵列doa估计，对应说明书具体实施方式(2)a和(2)b中的内容，将bessel先验稀疏贝叶斯模型[13]应用到了互质阵列误差校正doa估计问题当中。

3)针对网格失配问题，为降低模型复杂度，提出了互质阵列的网格失配求根算法，该方法可适用于更为稀疏的网格，并且运算复杂度更低。对应说明书具体实施方式(2)c部分中的内容，针对互质阵列的结构特点，进行了网格失配求根处理方法[14]的改进升级。

附图说明

附图1是贝叶斯结构模型图。

附图2是耦合误差条件下信噪比变化对算法性能的影响，其中子图(a)表示rmse随信噪比的变化，子图(b)表示成功率随信噪比的变化，子图(c)表示运算时间随信噪比的变化。

附图3是耦合误差条件下采样点数变化对算法性能的影响，其中子图(a)表示rmse随采样点数的变化，子图(b)表示成功率随采样点数的变化，子图(c)表示运算时间随采样点数的变化。

附图4表示幅相误差条件下信噪比变化对算法性能的影响，其中子图(a)表示rmse随信噪比的变化，子图(b)表示成功率随信噪比的变化，子图(c)表示运算时间随信噪比的变化。

附图5表示幅相误差条件下采样点数变化对算法性能的影响，其中子图(a)表示rmse随采样点数的变化，子图(b)表示成功率随采样点数的变化，子图(c)表示运算时间随采样点数的变化。

附图6表示位置误差条件下信噪比变化对算法性能的影响，其中子图(a)表示rmse随信噪比的变化，子图(b)表示成功率随信噪比的变化，子图(c)表示运算时间随信噪比的变化。

附图7表示位置误差条件下采样点数变化对算法性能的影响，其中子图(a)表示rmse随采样点数的变化，子图(b)表示成功率随采样点数的变化，子图(c)表示运算时间随采样点数的变化。

具体实施方式

1)阵列误差存在时的一般模型

a)阵元位置误差存在时的信号模型

当阵列位置误差存在时，可得互质阵列的输出信号模型为：

y(t)＝ap(θ)x(t)+n(t)(1)

式中，令y(t)为阵列输出y的第t列，为来波信号的第t列，t∈[l]，ap(θ)为含有阵元位置误差的阵列流行矩阵。设为互质阵列个阵元的阵元位置误差矢量，d0＝λ/2为基本阵元间距，可得ap(θ)的表达式为：

在doa估计中，通常考虑阵元的相对位置差，可得阵元位置误差的理论解集为系数为由个1组成的矢量，为增强求解的唯一性，选择第一个阵元为基准阵元，计算其它阵元与第一个阵元的相对位置误差，即设为待估计的相对阵元位置误差矢量，cp＝diag([0,cp])，ap1(θ)＝a(θ)diag([j2πd0sinθ1/λ0,...,j2πd0sinθg/λ0])，a(θ)同上文为误差情况下的阵列流行矩阵，当阵元位置误差较小时，对处进行一阶泰勒展开，可得：

ap(θ)＝a(θ)+cpap1(θ)(3)

式中：

式中，为与cp无关的参数矩阵。对式(5)关于cp求导，可得：

式中，为的第i列，只有第(i+1,i+1)个元素为1，其它元素均为0，cp,i为cp的第i个元素。将式(4)代入式(1)，可得阵元位置误差存在时的信号模型为：

b)阵元幅相误差存在时的信号模型

当阵元幅相误差存在时，互质阵列的输出信号模型为：

y(t)＝ag(θ)x(t)+n(t)＝cga(θ)x(t)+n(t)(8)

式中，和分别为互质阵列个阵元的幅度增益误差和初始相位误差，ag(θ)为包含幅相误差的阵列流行矩阵，其表达式为：

类似于阵元位置误差的情况，幅相误差的理论解集为cge＝b0cg，系数且b0≠0，为增强求解的唯一性，选择第一个阵元为基准阵元，计算其它阵元与第一个阵元的相对误差，即α1＝1，对式(8)中cga(θ)x(t)进行展开，可得：

式中，

设对式(11)关于cg求导，可得：

式中，为的第i列，只有第(i+1,i+1)个元素为1，其它元素均为0，cg,i为cg的第i个元素，将式(10)代入式(8)，可得阵元幅相误差存在时的信号模型为：

c)阵元耦合存在时的信号模型

类似于幅相误差存在的情况，阵元耦合误差也是一种乘性误差，设阵元耦合矩阵为cc，ac(θ)为包含阵元耦合误差的阵列流行矩阵，此时式(8)的信号模型可改写为：

y(t)＝ac(θ)x(t)+n(t)＝cca(θ)x(t)+n(t)(14)

设cc,ij为cc的第i行第j列元素，即阵元i和阵元j的耦合系数。当两个阵元的间距大于一定距离时，可忽略阵元耦合效应，设mmax为忽略耦合效应的临近距离系数，为耦合系数矢量，可得：

式中，di和dj分别为阵元i和阵元j的位置，当m＝0时，易得cc,0＝1。文献[7]针对均匀线阵的结构，给出了一般模型，但并不适用于结构上有较大差异的互质阵列，为更加直观阐述互质阵列和均匀线阵的阵元耦合矩阵差异，进行举例说明。设有cacis型互质阵列，共有个物理阵元，阵列系数m＝2,n＝3,p＝2，基本阵元间距为λ/2，mmax＝2，其阵元耦合矩阵cc为：

对于阵元数和基本阵元间距相同的均匀线阵，当mmax＝2时，其阵元耦合矩阵为：

对比式(16)和式(17)可见，阵元数相同的均匀线阵和互质阵列，其阵元耦合矩阵存在较为明显的差异。均匀线阵由于阵元间距相同，其阵元耦合矩阵是toeplitz矩阵，具有明显的结构特征，而互质阵列由于阵元位置的稀疏性，其阵元耦合矩阵不具备toeplitz性，耦合系数所在位置不确定性强，只能通过式(15)来确定非零元素所在位置。

类似阵元幅相误差存在时的处理方法，可得阵元耦合存在下的信号模型为：

式中，

对式(19)关于cc求导，可得：

式中，为的第i列，gci,kj为gci的第k行第j列元素，可得：

综合式(7)、式(13)和式(18)可知，对于互质阵列，当只有阵元位置误差、阵元幅相误差或阵元耦合误差存在时，可得一般化的阵列误差信号模型为：

y(t)＝a(θ)x(t)+qtc+n(t)(22)

式中，qt和c因误差的形式而有所差异。利用式(22)可将一般化的误差参数矢量c从含有误差的阵列流行矩阵中分离出来，使阵列流行矩阵降级为无误差条件下的阵列流行矩阵a(θ)，便于后续doa估计算法进行阵列误差条件下的doa估计和误差参数的估计。

2)基于bessel先验的sbl阵列校正算法

a)参数的概率密度分布

基于式(22)给出的一般化阵列信号误差模型，设空域网格为g为网格个数，x(t)的空域稀疏模型为接收信号可稀疏表示为：

设接收信号y(t)服从均值为方差为的复高斯分布，即可得的概率密度函数为：

式中，设噪声方差参数α0参数为a和b的伽马分布，其概率密度函数为：

设服从零均值，方差为γ＝diag(γ)的先验复高斯分布，γ＝[γ1,...,γg]为非负向量，的条件概率密度函数为：

式中，为的第i个元素。设超参数γ服从参数ε和η的伽马分布，概率密度函数为：

对于阵元位置误差参数cp，由于取值具有随机性，可近似为干扰位置信息的高斯噪声。故设cp服从零均值，方差为σ^-1的高斯分布，概率密度函数为：

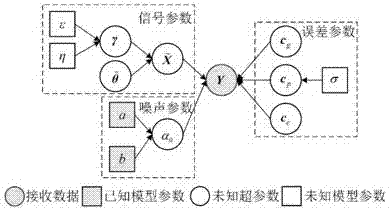
不同于阵元位置误差参数cp，幅相误差参数cg和阵元耦合误差cc的成因更为复杂且均为复数，尚难以用概率分布模型进行描述，故直接将cg和cc作为模型参数。图1给出了表征各参数关系的贝叶斯结构模型图。

由图1可知，接收数据y是由信号参数、噪声参数和误差参数共同表征的，其中噪声方差参数a和b已知，不进行更新，其它变量均为未知变量。此外，为降低网格失配的影响，本发明将网格作为一个未知超参数并进行更新，这一处理方式较之前章节所用方法降低了模型的复杂度和参数间的关联影响，更适合阵列误差条件下的网格失配doa估计问题。

b)稀疏贝叶斯学习

设服从均值为μ(t)，方差为σ的后验复高斯分布，即其中μ(t)和σ的表达式分别为：

式中，根据式(24)～(28)可得联合概率密度函数为：

根据贝叶斯公式，可得后验概率密度函数为：

式中，可见p(y)独立于超参数和模型参数ξ＝[ε,η,σ]。由文献[8]可知，θ的最大后验估计和ξ最优解为：

式中，

式中，表示关于后验概率密度函数的期望，下文用<·>进行简化表示。下面对未知参数的求解过程进行介绍。

(1)更新误差参数cp和σ

对于位置误差参数cp，式(33)等价为：

对式(35)进行化简，可得：

对式(36)关于cp,k求导，可得：

令可得：

对式(38)化简并求cp,k，可得第i次迭代cp,k的估计值为：

结合式(6)、式(29)和式(30)，可得和的表达式分别为：

式(40)～式(42)中，上式的推导利用了迹的乘法公式a^hba＝tr(baa^h)。

对于参数σ，式(33)等价为：

对式(43)展开，可得：

式中const为σ无关项，对(44)关于σ求导并令导数为0，可得第i次迭代σ的估计值为：

当阵元耦合误差或幅相误差存在时，误差参数的求解思想不变，式(39)改写为：

易得，式(40)～式(42)的推导过程与误差类型无关。因此，对于其它两种误差，将替换为即可沿用式(40)～式(42)的方法求得和其中上标g/c表示可为g或者c，即或者下文同理。

(2)更新噪声参数α0

对于噪声参数α0，式(33)等价为：

对式(48)展开，可得：

式中，const为与α0无关项。对式(49)关于α0求导并令导数为0，可得第i次迭代α0的估计值为：

(3)更新信号参数γ、ε和η

对于超参数γ，式(33)等价为：

对式(51)展开，可得：

式中const为与γk无关项，μk(t)为μ(t)的第k个元素，σkk为σ的第k行，第k列个元素。对式(52)关于γk求导并令导数为0，可得第i次迭代γk的估计值为：

对于参数ε和η，式(33)等价为：

对式(54)进行化简，可得：

对式(55)分别关于ε和η求导并令导数为0，可得：

式(56)中，ψ(ε)为digamma函数代表lnγ(ε)在ε处的导数，通过求解式(56)可得ε的在第i次迭代的更新值ε⁽ⁱ⁾。η在第i次迭代的更新值直接由式(57)给出。

c)网格失配求根处理

由于网格失配现象只发生在真实到达角的临近网格，对距离真实到达角较远的网格进行更新并不会对结果产生较大影响。因此，为提高算法效率，在进行网格参数的更新之前，首先对待更新的网格位置进行选择。由于信号个数通常未知，考虑到初始迭代过程中算法并未收敛，选择重构信号所有谱峰所在网格作为待更新的网格，设选定的网格编号集为g⁽ⁱ⁾，未被选定的网格不进行更新。

对于网格变量式(34)等价为：

对式(58)进行展开，并化简可得：

式中const为与无关项，为的第k列，为中间变量k∈g⁽ⁱ⁾。对式(59)关于vk求导，可得：

式中，综合式(60)和式(61)，可得：

式中，tk和fk为中间变量，fkj为fk的第j个元素，tk和fk的表达式分别为：

由于d1＝0，可将式(62)表示为矩阵相乘的形式：

式(65)是关于vk的多项式和，vk的最高阶数为系数为由于互质阵列通常满足即式(65)中vk的最高阶数大于系数矩阵wk的维数。在实际应用中，为便于多项式求根，需要对系数矩阵进行维度扩展，使其维数等于

设d1的第n个元素d1n为d2的第j个元素d2j为扩展后的系数矩阵的第j个元素为：

此外，对于阶的多项式求根会得到个解，需要进行解的筛选。由于可将|vi|＝1作为限制条件进行解的筛选。综合可得第i次迭代vk的估计值为：

式中，表示系数为的多项式的根，得到后可反解出为：

由于的求解结果具有不确定性，为避免的计算偏差造成结果发散，对的可靠范围进行约束以保证算法具有较强的收敛性。当存在网格失配时，设信号的真实到达角距网格最近，可得：

式(69)的含义为：当距网格最近时，选择作为的更新值，此时可降低网格失配的影响；当不在网格的附近时，网格估计值已经偏离了真实doa所在位置，为增强收敛速度，令的值同i-1次迭代保持不变，不接受作为的更新值。

d)算法步骤

当迭代终止后，设p＝[p1,...,pg]为重构的信号功率谱，可得：

搜索p的谱峰所在位置，设谱峰所在网格编号集为g，则信号到达角的估计值θe为：

综合上述，在实际应用中，利用br-sbac算法进行阵列误差条件下的doa估计大致分为参数初始化、参数迭代和doa估计三个步骤，doa估计指从重构信号谱中选出谱峰，将谱峰所在网格作为doa估计值。为便于理解，表1给出了利用br-sbac算法进行阵元位置误差校正的步骤，其它阵列误差的校正方法同理。

表1利用br-sbac算法进行阵元位置误差校正步骤

4)方法效果和其他方法的对比分析

由于不同阵列误差间具有一定的独立性，对阵元耦合误差条件、阵列幅相误差条件、阵元位置误差条件分别进行仿真实验，通过仿真实验进一步分析不同信噪比和采样点数条件下所提br-sbac算法性能。仿真所用阵列采用cacis型互质阵列，共有10个阵元，其中子阵1位置[0,3,6,9,12]d，子阵2位置[0,5,10,15,20,25]d，d为来波信号波长的一半。仿真实验不再单独分析误差参数的估计精度，通过doa估计效果来表征算法性能。仿真软件为matlabv.2014a，电脑系统为windows8.1，cpu为i3-2120，8g内存。

(1)阵列耦合误差条件

为对比算法性能，采用耦合误差条件下的sbac算法[7]、cma-es[9]算法、ogsbi算法[10]和阵元耦合条件下的crlb作为对比。br-sbac、ogsbi和sbac的最大迭代次数itermax＝500，迭代终止门限τ＝1×10^-4，噪声初始值γ⁽⁰⁾＝0，br-sbac算法的ε⁽⁰⁾＝0，η⁽⁰⁾＝1，cma-es算法的参数和初始值设定同文献[9]，稀疏重构算法的网格范围为[-90°,90°]。实验中sbac的网格间隔采用r＝1°和r＝4°两种情况，用sbac(r＝1)和sbac(r＝4)进行表示，br-sbac和ogsbi算法的网格间隔为r＝4°。

首先进行采样点数固定，信噪比变化条件下的仿真实验。设有3个相互独立的远场窄带信号，到达角分别为[11°+2δθ,-25°-3δθ,52°+2δθ]，δθ在-5°～5°的范围内随机取值，以排除角度先验信息对算法性能的影响。设信噪比的变化范围为-6db到10db，步长为2db，采样点固定为50，每个信噪比进行500次蒙特卡洛实验，统计doa估计的成功率、计算估计成功时的rmse和记录每种算法的运算时间，结果如图2。

由图2(a)可知：①随着信噪比的升高，除ogsbi算法外，其它三种算法的rmse均有不同程度的降低，br-sbac算法的rmse降低幅度最大，cma-es算法由于受参数设置和初始值的影响，doa估计精度随信噪比的提升相对较慢；②当信噪比大于-3db时，br-sbac算法的rmse低于四种比较算法，随着信噪比的增大逐步趋近于crlb，达到了较高的doa估计精度；③同sbac(r＝4)算法对比，尽管网格间隔相同，但br-sbac算法在doa估计精度上有明显提升，验证了所用bessel先验稀疏贝叶斯模型和网格失配求根处理方式的有效性。

由图2(b)可知：在不同信噪比条件下，br-sbac算法和sbac(r＝1)算法的成功率均接近为100％，高于其他算法，而适用于常规情况的ogsbi算法的检测成功率始终较低。

由图2(c)可知：①在不同信噪比条件下，br-sbac算法的运算时间少于图2(a)和(b)中表现较好的cma-es算法和sbac(r＝1)算法，而ogsbi和sbac(r＝4)两种方法的运算时间虽然较少，但在doa估计精度和成功率上却相对较差；②并且随着信噪比的升高br-sbac算法的运算时间有较为显著的下降趋势，当信噪比大于6db时，其运算时间同ogsbi算法接近，由于br-sbac算法每次迭代的运算量相同，可见高信噪比条件下，br-sbac算法的收敛速度也会加快。

下面进行信噪比固定，采样点变化条件下的仿真实验。设采样点的变化范围为20到200，步长为20，信噪比固定为0db，每个采样点进行500次蒙特卡洛实验，其它实验条件和算法参数设置同图2中信噪比变化的情况，统计doa估计的成功率、计算估计成功时的rmse和记录每种算法的运算时间，结果如图3所示。

由图3(a)可知：随着采样点数的增加，除ogsbi算法外，其它三种算法的doa估计精度均有不同程度的提升，br-sbac算法始终优于其它算法并且逐步接近crlb。可见，阵元耦合误差条件下，br-sbac算法的测向精度对采样点数的依赖度低，在采样点数较少时即可达到较高的doa估计精度。

由图3(b)可知：类似于图1(b)中信噪比变化的情况，br-sbac和sbac(r＝1)的成功率始终接近100％；cma-es算法虽然在成功分辨时具有较高的doa估计精度，但是分辨的成功率却只有85％～90％，不如br-sbac算法；ogsbi算法在不同采样点条件下的成功率仍为最低。

由图3(c)可知：①随着采样点数的增加，br-sbac、sbac(r＝1)和sbac(r＝4)算法的运算时间近似线性增长；②br-sbac算法的运算时间仍低于sbac(r＝1)算法1s左右，在采样点数小于200时也低于cma-es算法，而sbac(r＝4)和ogsbi算法虽然运算时间优于br-sbac算法，但doa估计成功率和精度均不够理想；③由于br-sbac算法的测向精度和成功率受采样点数影响较小，实际应用中可采用较少的采样点，降低运算时间随采样点数线性增加的负面影响。

(2)阵元幅相误差条件

为对比算法性能，采用幅相误差条件下的sbac算法[7]、s-tls算法[11]、ogsbi算法[10]和阵元幅相误差条件下的crlb作为对比。br-sbac、ogsbi和sbac算法的参数设置同耦合条件下的实验，s-tls算法的参数设置同文献[11]。实验中sbac的网格间隔仍采用r＝1°和r＝4°两种情况，沿用sbac(r＝1)和sbac(r＝4)的表示方法，br-sbac和ogsbi算法的网格间隔为r＝4°，s-tls算法的网格间隔为r＝1°。

首先进行采样点数固定，信噪比变化条件下的仿真实验。设有3个相互独立的远场窄带信号，到达角分别为[11°+2δθ,-25°-3δθ,52°+2δθ]，δθ在-5°～5°的范围内随机取值。设信噪比的变化范围为-6db到10db，步长为2db，采样点固定为50，每个信噪比进行500次蒙特卡洛实验，统计doa估计的成功率、计算估计成功时的rmse和记录每种算法的运算时间，结果如图4所示。

由图4(a)可知：①随着信噪比的升高，br-sbac和sbac(r＝1)算法的性能会有提高，br-sbac算法的提升幅度更为明显，当信噪比大于-4db时，br-sbac算法的rmse低于其它四种比较算法并逐步稳定于0.45左右；②sbac(r＝4)算法的doa估计精度较差，doa估计精度不如未进行误差校正的ogsbi算法，可见sbac算法对于稀疏重构网格宽度具有较高的依赖；③同crlb相比，br-sbac算法仍有一定差距，rmse平均相差0.39，算法的doa估计精度仍有进一步的提升空间。

由图4(b)可知：br-sbac和sbac(r＝1)两种算法始终保持较高的成功率，当信噪比大于-6db时，成功率接近于100％；s-tls算法成功率次之保持在90％之上；ogsbi算法在不同采样点条件下的成功率仍为最低，难以得到令人满意的doa估计结果。

由图4(c)可知：当信噪比大于2db时，br-sbac的运算时间会有较为明显的下降并少于sbac(r＝1)算法，当信噪比为10db时，接近s-tls算法。可见，当信噪比较高时，br-sbac算法在运算时间方面更为理想，而低信噪比条件下，虽然可以得到较高的doa估计精度，但仍需进一步提升运算效率。

下面进行信噪比固定，采样点变化条件下的仿真实验。设采样点的变化范围为20到200，步长为20，信噪比固定为0db，每个采样点进行500次蒙特卡洛实验，其它实验条件和算法参数设置同图4中信噪比变化的情况，统计doa估计的成功率、计算估计成功时的rmse和记录每种算法的运算时间，结果如图5所示。

由图5(a)可知：①在不同采样点数条件下，br-sbac算法的性能始终优于其它四种比较算法，当采样点数大于60时，rmse稳定于0.42左右；②sbac(r＝1)和s-tls算法的rmse随采样点数的变化趋势类似于br-sbac算法，但rmse分别平均高0.12和0.27；③br-sbac算法的rmse较crlb仍有一定差距，平均高0.34，虽然优于其它比较算法，但仍有很大的提升空间。

由图5(b)可知：br-sbac和sbac(r＝1)算法的成功率最优，当采样点数大于40时接近100％，ogsbi算法的成功率最低，虽然随着采样点数的增大有明显增加，但仍低于进行阵元幅相误差校正的其它算法。由图5(c)可知：在运算时间上，br-sbac算法略高于sbac(r＝1)算法，并且随采样点数的增加两种算法的运算时间仍有较为明显的上升。

(3)阵元位置误差条件

为对比算法性能，采用阵元位置误差条件下的sbac算法[7]、bi-affine算法[12]、ogsbi算法[10]和阵元位置误差条件下的crlb作为对比。br-sbac、ogsbi和sbac算法的参数设置同耦合误差的情况，bi-affine算法的参数设置同文献[12]，实验中sbac的网格间隔采用r＝1°和r＝4°两种情况，沿用sbac(r＝1)和sbac(r＝4)的表示方法，br-sbac和ogsbi算法的网格间隔为r＝4°，bi-affine算法的网格间隔为r＝1°。

首先进行采样点数固定，信噪比变化条件下的仿真实验。设有3个相互独立的远场窄带信号，到达角分别为[11°+2δθ,-25°-3δθ,52°+2δθ]，δθ在-5°～5°的范围内随机取值。设信噪比的变化范围为-6db到10db，步长为2db，采样点固定为50，每个信噪比进行500次蒙特卡洛实验，统计doa估计的成功率、计算估计成功时的rmse和记录每种算法的运算时间，结果如图6所示。

由图6(a)可知：①在信噪比为-6到0db的区间内，br-sbac算法的doa估计精度随信噪比的增加有明显提升，当信噪比大于-2db时，br-sbac算法的rmse低于其它四种比较算法并逐步稳定于0.41左右，达到了较高的doa估计精度；②同crlb相比，br-sbac算法的rmse平均相差0.33，这一差距和仿真条件中位置误差大小直接相关。可见，较已有方法br-sbac算法具有更高的doa估计精度，但当阵元位置误差较大时，算法的性能仍有进一步提升的空间。

由图6(b)可知：阵元位置误差条件下br-sbac的成功率有所下降，但最低仍有90％的成功率，高于rmse最为接近的sbac(r＝1)算法，并且随着信噪比的增加，成功率也会逐步增加并最终趋近于100％。

由图6(c)可知：①五种算法的运算时间有着较为明显的区分，br-sbac算法的运算时间仅高于doa估计精度和成功率均较差的sbac(r＝4)和ogsbi算法，并且随着信噪比的增加br-sbac算法的运算时间仍具有减少的趋势；②bi-affine算法虽然在低信噪比条件下具有较高的doa估计精度和成功率，但运算时间在五种算法中最长，接近br-sbac算法的一倍。

下面进行信噪比固定，采样点变化条件下的仿真实验。设采样点的变化范围为20到200，步长为20，信噪比固定为0db，每个采样点进行500次蒙特卡洛实验，其它实验条件和算法参数设置同图6中信噪比变化的情况，统计doa估计的成功率、计算估计成功时的rmse和记录每种算法的运算时间，结果如图7所示。

由图7(a)可知：①类似幅相误差存在的情况，在不同采样点条件下，br-sbac算法的rmse虽较crlb仍有一定差距，但低于其它四种比较算法，同现有算法相比具有更高的测向精度；②br-sbac算法的测向精度受采样点数的影响不大，当采样点数大于40时，算法的rmse即可逐步稳定于0.44左右。

由图7(b)可知：①总体来看，五种算法的doa估计成功率随着采样点数的增加均有不同程度的上升，其中br-sbac、sbac(r＝1)和bi-affine三种算法在采样点数大于20时即可达到90％的成功率；②相比之下，ogsbi和sbac(r＝4)算法的成功率较低，效果并不理想。

由图7(c)可知：①br-sbac算法的运算时间仍少于sbac(r＝1)算法和bi-affine算法，而bi-affine算法虽然成功率较高，但在rmse和运算时间方面表现均不如br-sbac算法；②较位置误差条件下，br-sbac算法的运算时间随采样点数增大的幅度要相对较慢，而sbac(r＝1)算法仍具有较为明显的线性上升趋势，原因主要为当采样点数增加时，br-sbac算法的收敛速度变快，部分抵消了采样点数增加对运算时间的影响。

references:

[1].boudaher,e.,etal.doaestimationwithco-primearraysinthepresenceofmutualcoupling.ineuropeansignalprocessingconference.2015.nice,france.

[2].boudaher,e.,etal.,mutualcouplingeffectandcompensationinnon-uniformarraysfordirection-of-arrivalestimation.digitalsignalprocessing,2017.14(03):p.3-14.

[3].han,k.,p.yanganda.nehorai.calibratingnestedsensorarrayswithmodelerrors.inasilomarconferenceonsignals,systemsandcomputers.2014.pacificgrove,ca,usa.

[4].han,k.,p.yanganda.nehorai,calibratingnestedsensorarrayswithmodelerrors.ieeetransactionsonantennasandpropagation,2015.63(11):p.4739-4748.

[5].koochakzadeh,a.andp.pal.sparsesourcelocalizationinpresenceofco-arrayperturbations.ininternationalconferenceonsamplingtheoryandapplications.2015.

[6].koochakzadeh,a.andp.pal,sparsesourcelocalizationusingperturbedarraysviabi-affinemodeling.digitalsignalprocessing,2017:p.15-25.

[7].liu,z.andy.zhou,aunifiedframeworkandsparsebayesianperspectivefordirection-of-arrivalestimationinthepresenceofarrayimperfections.ieeetransactionsonsignalprocessing,2013.61(15):p.3786-3798.

[8].wipf,d.p.andb.d.rao,anempiricalbayesianstrategyforsolvingthesimultaneoussparseapproximationproblem.ieeetransactionsonsignalprocessing,2007.55(7):p.3010-3022.

[9].boudaher,e.,etal.,mutualcouplingeffectandcompensationinnon-uniformarraysfordirection-of-arrivalestimation.digitalsignalprocessing,2017.61(2):p.3-14.

[10].yang,z.,l.xieandc.zhang,off-griddirectionofarrivalestimationusingsparsebayesianinference.ieeetransactionsonsignalprocessing,2013.61(1):p.38-43.

[11].han,k.,p.yanganda.nehorai,calibratingnestedsensorarrayswithmodelerrors.ieeetransactionsonantennasandpropagation,2015.63(11):p.4739-4748.

[12].koochakzadeh,a.andp.pal,sparsesourcelocalizationusingperturbedarraysviabi-affinemodeling.digitalsignalprocessing,2017.61(2):p.15-25.

[13].pedersen,n.l.,etal.,sparseestimationusingbayesianhierarchicalpriormodelingforrealandcomplexmodels.signalprocessing,2015.115(41):p.94-109.

[14].dai,j.,etal.,rootsparsebayesianlearningforoff-griddoaestimation.ieeesignalprocessingletters,2017.24(1):p.46-50.