纠正静止卫星地表上行长波辐射产品热辐射方向性的方法

本发明涉及一种纠正静止卫星地表上行长波辐射产品热辐射方向性的实用化方法，可用于静止卫星地表上行长波辐射产品的角度订正，属于空间信息技术领域。

背景技术：

地表上行长波辐射遥感产品被广泛地应用于水文、生态、气象、环境等领域，是表征地球冷暖的直接指标，是地表辐射收支的四分量之一。以goes-16、msg、himawari-8、fengyun-4为代表的静止卫星都设置了热红外通道以观测地球表面的上行长波辐射。由于静止卫星只能从固定的角度对地观测，目前利用静止卫星大气层顶亮度温度估算地表上行长波辐射的算法均假设地表热辐射是各向同性的，即认为从某个方向观测信号反演的地表上行长波辐射与地面实测的半球积分的上行长波辐射相等。

然而，地面、航空、卫星尺度的研究均表明地表热辐射是非各向同性的，并将这种现象称之为热辐射方向性。对于具备复杂三维结构的异温像元，热辐射方向性可导致不同方向观测到的方向亮度温度差异高达10k，严重制约了地表上行长波辐射产品的精度。即使在均一的沙漠、水面等地表，亦存在着显著的热辐射方向性现象。热辐射方向性现象在夏季比冬季突出、在白天比夜晚突出、在稀疏植被比浓密植被突出，已有研究表明回避热辐射方向性最大可导致地表上行长波辐射产品产生10％的估算误差。

因此，针对不同的地表类型(植被、城市、土壤、水体、冰雪等)，国内外研究者提出了诸多的物理模型来刻画热辐射方向性现象，建立方向亮度温度与地表结构、属性、光谱、温差等参数之间的关系，并试图用来纠正地表上行长波辐射产品的角度效应。然而这些物理模型因为需要的驱动参数太多导致不能实用化，于是近些年来提出了热红外波段的半经验半物理模拟模型，直接通过输入多个方向亮温/温度实现核系数的求解及任意方向的亮温/温度的计算，将半球所有方向的亮温计算出来之后，可以通过半球积分实现地表上行长波辐射的准确估算。目前的热红外半经验半物理模拟模型主要有8个：三参数的ross-li模型、rl模型、lsf-li模型和vinnikov模型，以及四参数的lsf-rl模型、lsf-chen模型、vinnikov-rl模型和vinnikov-chen模型。四参数的模型精度明显优于三参数模型，但是这些模型均为静态模型，即要求输入准同步的3-4个角度的热红外观测数据，以保证地表温度状态的稳定性。

对于某个像元，静止卫星的观测角度不变，而太阳角度在一天之内会发生变化，可构成多角度数据集，然而该多角度数据集并非准同步的，因为地表温度状态会随着光照条件的变化而变化且同时受到热惯量影响，通常表现为上午增温下午降温的趋势。由于动态热辐射方向性半经验半物理模型的缺乏，目前国内外尚没有实用化的方法能够有效地利用静止卫星的动态多角度信息纠正其热辐射方向性。

技术实现要素：

为了解决上述技术所存在的不足之处，本发明提供了一种纠正静止卫星地表上行长波辐射产品热辐射方向性的方法。

为了解决以上技术问题，本发明采用的技术方案是：一种纠正静止卫星地表上行长波辐射产品热辐射方向性的方法，包括以下步骤：

步骤一、利用经典的多波段大气层顶辐亮度直接估算法，计算晴空条件下静止卫星地表上行长波辐射的初值sulre(t)；

步骤二、利用日变化模型拟合步骤一估算的地表上行长波辐射初值,得到四个日变化模型的系数初值，并以其为基础限定地表上行长波辐射真值sulrm(t)的日变化参数范围；

步骤三、时间相关角度相关的热辐射方向性修正项trd(t)的建模；

步骤四、联立前三个步骤的结果求解六个未知数，包括日变化模型的四个未知数以及热辐射方向性建模的两个未知数；

步骤五、利用步骤四求解的四个日变化参数计算地表上行长波辐射真值；

步骤六、利用地面实测数据对步骤五的结果进行验证，选用的评价指标包括均方根误差rmse及平均偏差mbe。

进一步地，步骤一的具体过程如下：

首先基于modtran大气辐射传输模型模拟不同地表温度、地表发射率、大气廓线情况下的多通道大气层顶辐射亮度(ltoa,1,ltoa,2…ltoa,n)以及地表上线长波辐射真值，然后利用多元线性回归方法可以得到每个通道的回归系数，如公式(1)所示：

sulre(t)＝(a0,a1,a2…an)^t·(1,ltoa,1(t),ltoa,2(t)…ltoa,n(t))

(1)

上式中，ltoa,1为第一个大气窗口波段的大气层顶辐亮度，ltoa,2为第二个大气窗口波段的大气层顶辐亮度，一般选取8.5，11和12微米三个特征波段，a1,a2…an分别为第一波段、第二波段…第n波段的拟合系数，a0为常数项。

进一步地，步骤二的具体过程如下：

日变化模型由白天段模型和夜晚段模型两部分组成，但由于夜晚的地表热辐射方向性较弱，因此仅纠正白天段的地表热辐射方向性现象，白天的sulr日变化可以用公式(2-3)所示的余弦函数来拟合：

sulre(t)＝sulr0+sulra·cos(π(t-tm)/ω)(2)

sulrm(t)＝sulr0’+sulra’·cos(π(t-tm’)/ω’)(3)

其中公式(2)用来拟合初始值sulre的日变化，公式3用来拟合纠正后的地表上行长波辐射sulrm的日变化，均具有4个系数，即日出时刻附近的初始地表上行长波辐射sulr0和sulr0’，变化幅度sulra和sulra’，最大地表上行长波辐射出现时刻tm和tm’，余弦半周期宽度ω和ω’；基于步骤一的估算结果可以得到sulr0，sulra，tm和ω，以此为基础，可以得到sulr0，sulra，tm和ω的初值以及取值范围：sulr0-100<sulr0’<sulr0+100；sulra-100<sulra’<sulra+100；tm-2<tm’<tm+2；ω-2<ω’<ω+2。

进一步地，步骤三的具体过程如下：

瞬时的角度相关的地表热辐射方向性建模主要考虑三个因素的影响：地表温差大小，地表结构以及观测方向与太阳方向之间的角度距离，其中地表温差大小影响热点幅度，地表结构影响热点宽度；地表结构可以认为在一天内不变；观测方向与太阳方向之间的角度距离可以用公式(5)解析计算；而地表温差则是时间相关量，其与太阳光的入射强度相关，且受到地表热惯量的影响，其可通过公式(4)进行计算：

trd(t)＝sulrm(t)·cosθs(t)·a·e^{-f(t)/(π·b)}

(4)

在公式(4)中，cosθs(t)用来表征一天之内不同时刻的太阳光照条件，sulrm(t)表示热惯量对地表温差变化的作用，a是缩放因子以约束trd(t)的最大值，b是用来表征热点宽度的场景结构相关量；公式(5)中的θs为太阳天顶角；θv为观测天顶角；和分别表示太阳方位角和观测方位角。

进一步地，步骤四的具体过程如下：

联立公式(1-5)可以得到如下方程：

sulre(t)-sulrm(t)＝trd(t)＝sulrm(t)·cosθs(t)·a·e^{-f(t)/(π·b)}

(6)

移项之后得到如下的公式：

sulre(t)＝sulrm(t)·(1+cosθs(t)·a·e^{-f(t)/(π·b)})

(7)

将公式(3)代入公式(7)得到以下结果：

sulre(t)＝(sulr0’+sulra’·cos(π(t-tm’)/ω’)·(1+cosθs(t)·a·e^{-f(t)/(π·b)})(8)

该公式共含有六个未知数，分别是日出时刻附近的初始地表上行长波辐射sulr0’，变化幅度sulra’，最大sulr出现时刻tm’，余弦半周期宽度ω’，缩放因子a和热点宽度b；当一天内的静止卫星有效观测不小于六个时，该方程可以直接求解；非线性求解需要为未知数赋初值和取值范围，前四个参数的范围在步骤二中已经确定，a和b的初值为：a＝0.05，b＝0.25，a和b的取值范围为：0<a<0.1，0<b<0.5。

进一步地，步骤五的具体过程如下：

由步骤四求得sulrm的四个日变化参数，即日出时刻附近的初始地表上行长波辐射sulr0’，变化幅度sulra’，最大sulr出现时刻tm’和余弦半周期宽度ω’，随后利用公式(3)计算sulrm(t)的真值，即热辐射方向性纠正后的地表上行长波辐射结果。

进一步地，步骤六的具体过程如下：

地面辐射表测量的参量就是半球积分的地表上行长波辐射值(sulrt)，在物理意义上与公式(3)中的sulrm完全一致，可以利用地面辐射表的观测值sulrt来对步骤五得到的纠正热辐射方向性的sulrm结果进行验证，选取的评价指标有2个，见公式(9-10)：

上式中，ti表示卫星观测时刻，t1和tn分别为起止和终止时刻。

本发明过提出时间相关角度相关的热辐射方向性修正项，有效利用了静止卫星一天内多次观测构成的多角度信息，实现了热辐射方向性的动态纠正，显著提高了静止卫星地表上行长波辐射的估算精度，解决了一直以来在估算静止卫星地表上行长波辐射中回避热辐射方向性的问题。本发明输入数据仅为静止卫星多时刻的大气层顶辐射亮度值，即可实现地表上行长波辐射中热辐射方向性误差与半球积分真值的分离，兼具准确性与简洁性。

附图说明

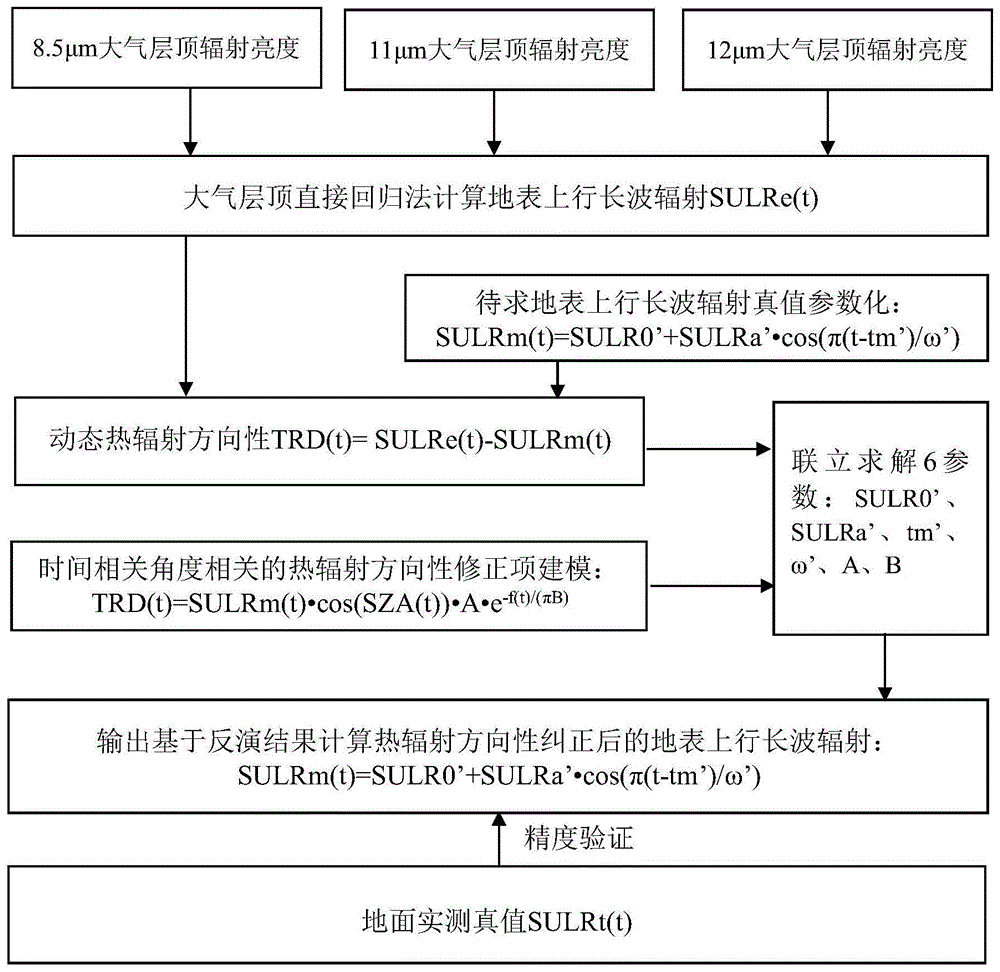
图1为本发明方法的整体流程图。

图2为基于goes-16abi数据的测试结果图。

图3为以sulrt为标准的sulre和sulrm的散点图。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细的说明。

图1所示的一种纠正静止卫星地表上行长波辐射产品热辐射方向性的方法，包括以下步骤：

步骤一、利用经典的多波段大气层顶辐亮度直接估算法，计算晴空条件下静止卫星地表上行长波辐射的初值sulre(t)；

步骤二、利用日变化模型拟合步骤一估算的地表上行长波辐射初值,得到四个日变化模型的系数初值，并以其为基础限定地表上行长波辐射真值sulrm(t)的日变化参数范围；

步骤三、时间相关角度相关的热辐射方向性修正项trd(t)的建模；

步骤四、联立前三个步骤的结果求解六个未知数，包括日变化模型的四个未知数以及热辐射方向性建模的两个未知数；

步骤五、利用步骤四求解的四个日变化参数计算地表上行长波辐射真值；

步骤六、利用地面实测数据对步骤五的结果进行验证，选用的评价指标包括均方根误差rmse及平均偏差mbe。

步骤一的具体过程如下：

大气窗口通道的大气层顶观测的辐亮度包含了地表上行长波辐射的有效信息，可以用来回归地表上行长波辐射的结果，首先基于modtran大气辐射传输模型模拟不同地表温度、地表发射率、大气廓线情况下的多通道大气层顶辐射亮度(ltoa,1,ltoa,2…ltoa,n)以及地表上线长波辐射真值，然后利用多元线性回归方法可以得到每个通道的回归系数，如公式(1)所示：

sulre(t)＝(a0,a1,a2…an)^t·(1,ltoa,1(t),ltoa,2(t)…ltoa,n(t))

(1)

上式中，ltoa,1为第一个大气窗口波段的大气层顶辐亮度，ltoa,2为第二个大气窗口波段的大气层顶辐亮度，一般选取8.5，11和12微米三个特征波段，a1,a2…an分别为第一波段、第二波段…第n波段的拟合系数，a0为常数项；

该方法由于其间接性和准确性已经成为目前生产全球地表上行长波辐射产品的主流算法，静止卫星一天内的多次观测可以直接多次使用该公式进行估算，得到动态的sulre结果，该结果基于单个方向的辐射亮度估算地表上行长波辐射，是受到地表热辐射方向性影响的量，与地表实测上行长波辐射真值之间存在偏差，可作为估算的初始值。

步骤二的具体过程如下：

地表温度及地表上行长波辐射日变化可以采用日变化模型来高精度刻画，日变化模型由白天段模型和夜晚段模型两部分组成，但由于夜晚的地表热辐射方向性较弱，因此仅纠正白天段的地表热辐射方向性现象，白天的sulr日变化可以用公式(2-3)所示的余弦函数来拟合：

sulre(t)＝sulr0+sulra·cos(π(t-tm)/ω)(2)

sulrm(t)＝sulr0’+sulra’·cos(π(t-tm’)/ω’)(3)

其中公式(2)用来拟合初始值sulre的日变化，公式3用来拟合纠正后的地表上行长波辐射sulrm的日变化，均具有4个系数，即日出时刻附近的初始地表上行长波辐射sulr0和sulr0’，变化幅度sulra和sulra’，最大地表上行长波辐射出现时刻tm和tm’，余弦半周期宽度ω和ω’；基于步骤一的估算结果可以得到sulr0，sulra，tm和ω，以此为基础，可以得到sulr0，sulra，tm和ω的初值以及取值范围：sulr0-100<sulr0’<sulr0+100；sulra-100<sulra’<sulra+100；tm-2<tm’<tm+2；ω-2<ω’<ω+2。

步骤三的具体过程如下：

瞬时的角度相关的地表热辐射方向性建模主要考虑三个因素的影响：地表温差大小，地表结构以及观测方向与太阳方向之间的角度距离，其中地表温差大小影响热点幅度，地表结构影响热点宽度；

对于静止卫星一天多次观测构建的多角度数据集而言，需要采用动态建模方法对热辐射方向性进行刻画，以同时考虑地表温差大小的时间相关性和观测方向与太阳方向之间角度距离的角度相关性；

地表结构可以认为在一天内不变；观测方向与太阳方向之间的角度距离可以用公式(5)解析计算；而地表温差则是时间相关量，其与太阳光的入射强度相关，且受到地表热惯量的影响，因此本发明提出了一个新的计算时间相关角度相关的热辐射方向性修正项trd(t)的方法，其可通过公式(4)进行计算：

trd(t)＝sulrm(t)·cosθs(t)·a·e^{-f(t)/(π·b)}

(4)

在公式(4)中，cosθs(t)用来表征一天之内不同时刻的太阳光照条件，sulrm(t)表示热惯量对地表温差变化的作用，a是缩放因子以约束trd(t)的最大值，b是用来表征热点宽度的场景结构相关量；公式(5)中的θs为太阳天顶角；θv为观测天顶角；和分别表示太阳方位角和观测方位角。

步骤四的具体过程如下：

联立公式(1-5)可以得到如下方程：

sulre(t)-sulrm(t)＝trd(t)＝sulrm(t)·cosθs(t)·a·e^{-f(t)/(π·b)}

(6)

移项之后得到如下的公式：

sulre(t)＝sulrm(t)·(1+cosθs(t)·a·e^{-f(t)/(π·b)})

(7)

将公式(3)代入公式(7)得到以下结果：

sulre(t)＝(sulr0’+sulra’·cos(π(t-tm’)/ω’)·(1+cosθs(t)·a·e^{-f(t)/(π·b)})(8)

该公式共含有六个未知数，分别是日出时刻附近的初始地表上行长波辐射sulr0’，变化幅度sulra’，最大sulr出现时刻tm’，余弦半周期宽度ω’，缩放因子a和热点宽度b；当一天内的静止卫星有效观测不小于六个时，该方程可以直接求解；非线性求解需要为未知数赋初值和取值范围，前四个参数的范围在步骤二中已经确定，a和b的初值为：a＝0.05，b＝0.25，a和b的取值范围为：0<a<0.1，0<b<0.5。

步骤五的具体过程如下：

由步骤四求得sulrm的四个日变化参数，即日出时刻附近的初始地表上行长波辐射sulr0’，变化幅度sulra’，最大sulr出现时刻tm’和余弦半周期宽度ω’，随后利用公式(3)计算sulrm(t)的真值，即热辐射方向性纠正后的地表上行长波辐射结果。

步骤六的具体过程如下：

地面辐射表测量的参量就是半球积分的地表上行长波辐射值(sulrt)，在物理意义上与公式(3)中的sulrm完全一致，可以利用地面辐射表的观测值sulrt来对步骤五得到的纠正热辐射方向性的sulrm结果进行验证，选取的评价指标有2个，见公式(9-10)：

上式中，ti表示卫星观测时刻，t1和tn分别为起止和终止时刻。

下面将结合具体的实施例，对本发明进行进一步的阐述。

实施例1、

goes-16是美国新一代goes-r系列静止卫星的首颗星，于2016年发射，2017年发布数据。其搭载的主要载荷abi可实现每15分钟一次的对地观测，第11、14和15波段的中心波长为8.5、11.2和12.3μm，利用这三个特征通道的大气层顶辐射亮度直接可以估算地表上行长波辐射的初始值sulre。利用本发明提出的方法可以进一步估算得到热辐射方向性纠正后的结果sulrm，利用美国通量ameriflux站点实测数据sulrt可以对sulrm的精度进行直接验证，以检验本发明的功效，具体实施方式见图1。

图2给出了利用abi大气层顶辐射亮度直接估算sulre的结果，包括地表上行长波辐射的初始估算结果(sulre)、考虑热辐射方向性的纠正结果(sulrm)及地面站点实测结果(sulrt)。如图2中圆圈所示，以及热辐射方向性纠正后的sulrm结果，如图2中绿色方框所示，站点实测sulr数据是每30分钟一次，如图2中星号所示，因此将估算的sulre和sulrm也采样成该时间频率，从上午9点到下午16点，每天包含15次观测。图2(a)-(d)分别给出的是该站点2019年08月30日、2019年08月26日、2019年08月13日、2019年08月12日的结果，sulre的rmse分别为22.9、28.5、23.2、18.7w/m2，sulrm的rmse分别降低为12.7、4.8、7.7、9.6w/m2，sulre的高估现象得到显著的抑制。

图3给出了全部4天(2019年08月30日、2019年08月26日、2019年08月13日、2019年08月12日，共60个点)估算结果的散点图，可以看出整体而言，sulre的rmse为23.6w/m2，sulrm的rmse为9.2w/m2，rmse大幅降低14.4w/m2，证明了本发明的有效性及先进性。

本发明首次提出了时间相关角度相关的热辐射方向性修正项，以其为基础构建了静止卫星地表上行长波辐射的六参数热辐射方向性纠正算法。基于goes-16静止卫星和ameriflux的站点实测验证表明，本发明有效抑制了热辐射方向性对地表上行长波辐射造成的误差，显著提高了地表上行长波辐射的精度。本发明在空间信息技术领域，尤其是地表能量平衡遥感领域具有重要的应用价值。

上述实施方式并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的技术方案范围内所做出的变化、改型、添加或替换，也均属于本发明的保护范围。