一种冷成形摩擦系数测定方法

1.本发明涉及一种冷成形摩擦系数测定方法，属于金属塑性成形技术领域。


背景技术：

2.冷锻模具与工件的接触表面存在着变形金属的塑性流动使得摩擦产生，摩擦本身是一种非常复杂的物理现象，而冷锻塑性变形过程中不断形成新的表面更是增加了其摩擦与润滑状态的复杂性。摩擦与润滑条件作为冷锻工艺过程的重要边界条件，直接影响金属的塑性流动与变形均匀性、成形力的大小与能量消耗、成形件的内部结构与表面质量，以及模具的使用寿命等。因此正确地理解摩擦与润滑机理、合理利用摩擦效应与优选相关润滑剂，对于冷锻工艺的顺利实施与冷锻件的批量生产具有重要的意义。
3.而目前对于冷成形摩擦系数的测定主要采用的是圆环镦粗法，该方法通过测量镦粗前后的圆环内径与高度，计算内径与高度的相对变化量，然后查询标定曲线获得具体摩擦系数或摩擦因子。该方法虽然能够实现摩擦系数的测定，但是若要想获得比较精确的摩擦系数或者摩擦因子，就要得到非常精细的标定曲线，而大量标定曲线的获取是一个繁琐的过程，且存在一定的误差。


技术实现要素：

4.本发明的目的是提供一种冷成形摩擦系数测定方法，以解决目前测定过程存在的效率低、误差大的问题。
5.本发明为解决上述技术问题而提供一种冷成形摩擦系数测定方法，该测定方法包括以下步骤：
6.1)将待测材料加工成摩擦试验所需要的试样结构，并对其进行润滑处理；
7.2)对润滑处理后的试样结构进行压缩变形试验，在试验过程中控制试样结构高度的相对缩减量在设定范围以内，并测量试样结构在压缩变形试验后的特征参数，所述的特征参数至少包括两个；
8.3)建立试样结构的有限元模型，根据所述压缩变形试验确定压下高度和压下速度；
9.4)以有限元测得的特征参数与试验测得的特征参数之间差异最小建立目标函数；
10.5)采用遗传算法对建立的目标函数进行求解，得到使有限元模型确定的特征参数与压缩变形试验测得的特征参数之间差异最小时对应的摩擦系数，该摩擦系数即为待测材料的摩擦系数。
11.本发明首先建立目标函数，使得有限元测得的特征参数与试验测得的特征参数之间差异最小，然后利用遗传算法对目标函数进行求解，通过有限元软件将每次遗传迭代出的摩擦系数代入到所建立的有限元模型中，进而得到对应的特征参数，并将其与试验测得的对应的特征参数进行比较，判断是否能够达到最优，若否，则对种群重新进行更新，直至能够找到最优的解对应的摩擦系数。本发明简单易行，可以直接获得待测工件材料与模具
接触面的摩擦系数，不需要进行标定曲线的制作，提高了效率；同时通过优化算法，避免了手工调整参数带来的随机性，提高了摩擦系数测定的精度。
12.进一步地，所述步骤5)采用的遗传算法为nsga-ii。
13.由于特征参数不止一个，为了保证得到摩擦系数能够使特征参数均能达到最优，本发明采用nsga-ii的遗传算法，使得到的摩擦系数能够满足各特征参数的要求，进一步提升摩擦系数的精度。
14.进一步地，所述的目标函数为：
15.y＝min((x-x
′
)/2)216.y为目标函数，x为通过有限元模型确定的特征参数，x
′
为试验测得的特征参数。
17.本发明采用的目标函数能够准确、直接描述特定的参数之间的关系，并有利于求解出满足目标的摩擦系数。
18.进一步地，为方便进行压缩试验，所述的试样结构为圆环或者外侧带凸台的圆环。
19.进一步地，为方便实现准确测量特征参数，当试样结构为外侧带凸台的圆环，所述的特征参数包括外凸台外径和高度。
20.进一步地，为避免压缩力度过大导致试样结构变形严重而难于进行特征参数的测量，所述的设定范围为30％-50％。
21.进一步地，为提高特征参数测量的准确性，所述步骤2)中在测量试验后的试样结构的特征参数时，对一个特征参数进行若干次测量，取若干次测量结果的平均值作为最终的特征参数。
22.进一步地，采用nsga-ii算法的求解过程如下：
23.a.初始化摩擦系数，生成对应的初始种群；
24.b.将初始种群对应的摩擦系数导入有限元模型中，按照设定的试验条件对有限元模型进行计算，得到对应的特征参数；
25.c.将有限元计算出的特征参数与试验测量得到的特征参数进行比较，判断结果是否满足收敛条件，若不满足，则对种群进行优化，将优化后的种群对应的摩擦系数导入到所述有限元模型中，重新计算对应的特征参数，直至计算出的特征参数与试验测量得到的特征参数之间的差值满足收敛条件，满足收敛条件的对应的摩擦系数即为待测材料的摩擦系数。
26.进一步地，种群优化过程如下：对初始种群进行非支配排序，对排序后的初始种群进行选择、交叉、变异操作得到第一代子代种群；将父代种群与子代种群合并，进行非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取对应的个体组成新的父代种群。
27.本发明在选择种群更新之前会根据个体间的支配关系进行分层，使好的个体有更大的机会遗传到下一代，从而让目标搜索向最优解集的方向进行；同时，通过拥挤度来比较算子，避免具有相同次序的个体在空间较近距离内聚集，从而使计算结果在目标空间内分布较为均匀，保障群体的多样性，克服超级个体的过度繁殖，防止过早收敛。
附图说明
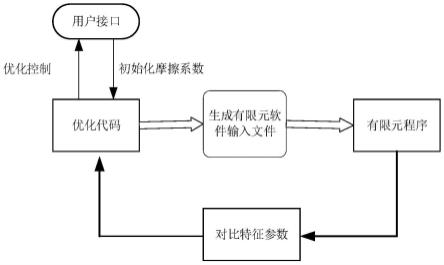
28.图1是本发明冷成形摩擦系数测定方法的原理图；
29.图2是本发明冷成形摩擦系数测定方法的流程图；
30.图3是本发明所采用的nsga-ii算法的实现流程图；
31.图4是本发明实施例中所加工的试样结构的尺寸示意图；
32.图5是本发明实施例中建立的有限元模型示意图；
33.图6是本发明实施例中优化过程的收敛曲线示意图；
34.图7-a是本发明实施例中所加工的试样结构的主视图；
35.图7-b是本发明实施例中所加工的试样结构的立体图；
36.图8-a是本发明实施例中压缩变形后的试样结构的主视图；
37.图8-b是本发明实施例中压缩变形后的试样结构的立体图。
具体实施方式
38.下面结合附图对本发明的具体实施方式作进一步地说明。
39.冷成形摩擦系数测定方法的实施例
40.本发明首先将待测材料加工成摩擦试验所需要的试样结构；然后进行润滑处理；再将该待测工件材料于平面模具中进行压缩变形；然后在有限元软件中建立相同条件下的压缩实验有限元模型，初始化待求的摩擦系数；选择优化算法作为最小化目标函数的识别策略，编写优化程序，不断自动调整摩擦系数调用有限元求解器来模拟压缩试验，对比有限元计算与实验测得的特征参数变化量，利用目标函数评估两者的误差，误差最小时对应的摩擦系数即为最优解。该方法的实现原理如图1所示，下面结合具体的实例来进行说明。
41.1.将待测材料加工成摩擦试验所需要的试样结构，并对其进行润滑处理。
42.本实施例中选用al1050铝作为测试工件材料，将待测工件材料做成试样结构，以进行实验测量。其中试样结构可选择常规摩擦试验的试样形状，如圆环、外侧带凸台的圆环、带内筋的圆环等。本实施例试样采用外侧带凸台的结构尺寸如图4所示，成品试样如图7-a和图7-b所示，其中图7-a为主视图，图7-b为立体图。测量待测材料关键尺寸，包括待测材料外径、外凸台外径与高度，用游标卡尺3次测量取平均值，本实施例中测量结果为：待测材料的外径为外凸台外径为高度5.988mm。
43.对做好的试样结构进行润滑处理，采用现有润滑介质与润滑方法对工件材料或模具表面进行润滑；润滑介质可以是液态润滑剂或固态润滑剂；润滑方法可以是机械、物理或化学的润滑方法。本实施例选择fuchs1905l润滑油作为润滑介质，并使用毛刷均匀地涂覆在上下平面模具上，实现对试样结构的润滑处理。
44.2.将该待测工件材料于平面模具中进行压缩变形，并控制工件材料高度的相对缩减量在设定范围以内，测量试验条件下的特征参数变化量。
45.本实施例在平面模具下，对试样结构进行压缩变形，使待测材料高度相对缩减量控制在40％。对本实施例而言，可采用预设压力机的行程或者试验机的压力量实现对试样结构高度的相对缩减量的控制。本实施例压缩变形后的试样结构如图8-a和图8-b所示，其中图8-a为主视图，图8-b为立体图，采用游标卡尺对压缩变形后的试样结构进行测量，主要是测量压缩变形后的待测材料的外凸台外径与高度，考虑到测量带来的误差，本实施例将采用多次测量结果的平均值作为最终的测量结果，本实施例测量得到待测材料的外凸台外径为高度为3.934mm。为避免压缩力度过大导致试样结构变形严重而难于进行
特征参数的测量，或者压缩力度过小无法有效测量，压缩变形的高度相对缩减量控制30％-50％。
46.3.根据设定的试验条件建立有限元模型，根据设定的高度的相对缩减量确定压下高度。
47.对步骤1中构建的待测材料的试样结构进行有限元建模，得到相应的有限元模型，如图5所示，对试样模型划分四面体网格、在对称面设置轴对称约束条件、设定有限元模拟所需要的材料本构模型(该模型由al1050铝的单向压缩试验测得的基础数据推导计算得到)以及记录模拟过程中尺寸变化的追踪点，对下砧板模型设置固定约束条件，对上砧板模型设置与试验相同的运动方向及载荷大小，最后设定试样模型与砧板模型之间的初始摩擦系数，从而实现对步骤2所述试验过程的有限元模拟。
48.4.构建目标函数，并求解。
49.本发明建立的使得有限元测得的特征参数与试验测得的特征参数之间差异最小的目标函数为：
50.y＝min((x-x
′
)/2)251.y＝min((x/x
′
)-1)252.其中y为目标函数，x为通过有限元模型确定的特征参数，x
′
为试验测得的特征参数。作为其他实施方式，这里的目标函数也可以有其他变形，只要能够准确描述通过有限元模型确定的特征参数和试验测得的特征参数之间的差异即可。
53.不同试样结构的测量的特征参数不只一个，若试样形状为带内筋的圆环，特征参数则为试样高度、内筋内径；若试样形状为外侧带凸台的圆环，特征参数则为试样高度、外凸台外径；若试样形状为圆环，特征参数则为试样高度、圆环内径；因此建立的目标函数也不只一个，即本发明建立的目标函数为多目标函数。由于本实施例中试样选用的是外侧带凸台的圆环，因此对应的测量特征参数包括待测材料的外凸台外径和高度，此时建立两个目标函数，一个是外凸台外径的误差，一个是高度的误差。其中外凸台外径的误差＝((外凸台外径的模拟值-外凸台外径试验值)/2)2，高度的误差＝((高度的模拟值-高度试验值)/2)2。
54.以上述两个误差函数最小为目标，建立双目标函数。对建立的目标函数进行求解，能够使两种测量特征参数误差最小的摩擦系数就是本发明最终需要确定的摩擦系数。
55.遗传算法(ga)是基于达尔文生物进化论发展而来的一种随机搜索算法。遗传算法被提出以后，在函数优化、生产调度、模式识别、神经网络、自适应控制等领域得到了广泛的应用，在这些领域遗传算法发挥了巨大的作用，提高了问题求解的效率。遗传算法是模拟一个人工种群的繁衍进化过程，通过选择、交叉以及变异等机制，在每次迭代中都保留一组优选个体，不断地重复这个过程，种群经过若干代的繁衍进化后，在理想情况下整个种群的适应度达到“近似最优”的状态。因此，本发明采用遗传算法以及改进的遗传算法对目标函数进行求解。对本实施例而言，先产生初始种群，将初始种群对应的摩擦系数作为初始摩擦系数，利用初始摩擦系数对试样结构进行有限元模拟，若试样结构采用外侧带凸台的圆环，圆环采用四面体实体单元，在对称面施加对称约束条件，下砧板固定，上砧板向下移动施加载荷，施加的载荷大小与试验过程相同，施加载荷完成后对有限元模型进行测定，得到模拟结束时的圆环高度和对应的外凸台外径尺寸，由于圆环外凸台不同节点对应的外径不完全相
同，因此圆环外凸台外径采用多个节点的平均值。将由有限元模拟测定出来的特征参数与步骤2中测量的对应的特征参数进行比较，若各特征参数的差异均满足设定要求，则认为该摩擦系数即为待测材料的摩擦系数，否则，需要对种群进行更新，直至找到满足设定条件的种群，将该种群对应的摩擦系数作为最终测定的摩擦系数。采用遗传算法的求解流程如图2所示。
56.nsga
‑ⅱ
算法是目前最流行的多目标遗传算法之一，它的运行速度快、解集收敛性好，nsga
‑ⅱ
算法在选择算子执行之前会根据个体间的支配关系进行分层，使好的个体有更大的机会遗传到下一代，从而让目标搜索向最优解集的方向进行。同时，它通过拥挤度来比较算子，避免具有相同次序的个体在空间较近距离内聚集，从而使计算结果在目标空间内分布较为均匀，保障群体的多样性，克服超级个体的过度繁殖，防止过早收敛。
57.当采用nsga
‑ⅱ
算法进行种群更新时，首先，随机产生规模为n的初始种群,非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；其次，从第二代开始，将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；最后通过遗传算法的基本操作产生新的子代种群，依此类推，直到满足程序结束的条件，如图3所示。其中对初始种群更新前进行非支配排序，对排序后的初始种群进行选择、交叉、变异操作得到第一代子代种群；将父代种群与子代种群合并，进行非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取对应的个体组成新的父代种群。
58.按照nsga
‑ⅱ
算法进行求解，其迭代次数和精度的关系如图6所示，从中可以看出，本发明采用nsga
‑ⅱ
算法对目标函数进行求解时，能够在100次迭代后使得目标函数达到最优，大大提高了求解的效率。