一种基于离散小波矩量法的地震散射波场数值模拟方法

1.本发明属于地震散射波偏移成像技术领域，具体涉及一种利用小波函数将lippmann
–
schwinger积分方程生成的线性方程组变成稀疏带状矩阵方法，特别涉及一种利用离散小波矩量法进行地震散射波场数值模拟的方法。


背景技术：

2.近年来，随着地震勘探逐渐转向复杂地质构造的偏移成像转变，如何有效利用散射波携带的地下介质信息，对复杂介质进行偏移成像逐渐受到重视。相应地，地震散射波场正演模拟技术作为全波场偏移和全波形反演的基础，对认识散射波场的时空分布特征及其与复杂构造之间的关系具有重要意义。利用lippermann-schwinger(ls)方程解决地震波散射问题时，传统的求解积分方程的矩量法计算复杂，离散后生成一个满秩的系数矩阵，需要求解大型线性方程组，计算量大，效率低。
3.针对积分方程法处理散射问题时所存在的问题，国内外学者在积分方程快速算法方面作了大量研究工作。《geophysical prospecting》2005年第03期公开了sun的“on the electrical reflectivity tensor in d.c.electric field modeling”，其借鉴电磁散射问题中的拟线性近似技术，通过假设散射波场与背景波场之间的线性关系，建立了声波散射的拟解析近似表达式。拟解析近似是半解析解，只需计算数值积分，该方法可以有效的避开复杂介质情况下大型线性方程组的求解。中国专利cn104112044a提出了一种超细线结构物体电磁特性的高效分析方法，通过使用区间小波作为矩量法中的基函数，并使用快速小波变换，在计算中得到稀疏矩阵，从而消除稠密矩阵所带来的弊端，达到比传统分析更精确、高效的效果。《地球物理学报》2021年第08期公开了徐杨杨等的“一种利用离散与fft快速褶积的散射地震波并行计算方法”，该文对原ls方程进行改写，构造等价ls方程并用法进行离散，根据格林函数矩阵的toeplitz性质，通过快速傅氏变换来加速矩阵向量乘积，达到降低存储和计算复杂的目的。
4.但是，利用矩量法解决地震波散射问题时，前人成果中，并没有提出针对传统矩量法计算效率进行提高和改进的方法和策略。小波函数在时域和频域上都具有很好的局部性，用小波进行数值计算可以在时域和频域上都获得较好的分辨率。积分或微分方程在小波基下展开后，便转化成一个关于小波系数的代数方程或方程组。小波函数特有的消失矩、正则性和紧支撑的性质，使小波分析通过选择合适的离散基函数或离散方式能够减少二维和三维问题用矩量法求解的时间。
5.连续小波矩量法是直接用连续小波函数及其尺度函数作为基函数和权函数的方法，并依据多分辨分解，把函数展开成小波级数，再利用矩量法确定展开系数的值。但连续小波矩量法公式推导复杂且小波函数通常无解析解，要通过频域方法、迭代法和离散化法等数值方法求解。基于此，急需研发一种新型矩量法，可以在求解离散线性方程组时有效降低存储和计算复杂度。


技术实现要素：

6.本发明的目的就在于提供一种基于离散小波矩量法的地震散射波场数值模拟方法，以解决传统矩量法在解lippermann-schwinger(ls)方程时，离散系数矩阵满秩导致占用存储空间大、计算效率低的问题。
7.本发明的目的是通过以下技术方案实现的：
8.首先，选取形式较为简单的正交分域基函数，对待求波场进行展开，通过矩量法将ls方程转化为矩阵方程；其次，选取具有较好消失矩、正则性和紧支撑的daubechie小波函数，利用mallat塔式分解算法得到daubechie小波滤波器，进而构造出正交小波变换矩阵对系数矩阵进行稀疏化，即得到关于小波展开系数的线性方程组；接着采用共轭梯度法求解该线性方程组；最后，对线性方程组的解向量进行小波逆变换，即得到待求波场的展开系数，进而求得计算区域上的待求波场值。
9.一种基于离散小波矩量法的地震散射波场数值模拟方法，包括以下步骤：
10.a、读入速度模型(模型大小nx*nz)，设置震源子波、背景速度；
11.b、积分区域(速度模型)ω均匀剖分(vj为第j个剖分面元)；取分片常函数空间(l2(ω)为hilbert空间)；构造标准正交基函数ej(r)，满足
[0012][0013]
c、根据步骤b的正交分域基函数ej(r)，对以速度扰动为权的位移场进行展开其中α＝α(r)＝c2/v2(r)-1(v(r)为介质速度)，u(r)位移场，得到近似算子方程：
[0014][0015]
其中，en是映l2(ω)到sn的正投影算子。为带权总位移场，为带权背景场，k0＝ω/c为背景波数(c为常速背景介质速度)，g＝g(r,r')为背景介质格林函数；
[0016]
d、选取步骤b中的分域基函数ej(r)作为矩量法的权函数。利用正投影算子的自共轭性质，方程两边同时与权函数作内积，
[0017][0018]
其中，(
·
，
·
)表示l2(ω)的内积。由此，通过矩量法得到系数{cj,j＝1,
…
,n}满足线性方程组
[0019]g′
c＝s
ꢀꢀꢀ
(4)
[0020]
其中，且
[0021]
e、选取daubechie小波函数，利用mallat塔式分解算法，通过daubechie小波滤波器构造出正交小波变换矩阵w；
[0022]
f、用步骤e得到的正交小波变换矩阵w对步骤d得到的系数矩阵进行小波变换，变换过程如下：
[0023][0024]
根据小波函数的紧支撑性、高阶消失矩特性，变换后矩阵中大部分小波系数为零或者值很小。设定阈值ε，在不影响计算精度的前提下忽略掉小于ε的值。采用一维索引只存储稀疏矩阵的非零元素可以降低内存。进而得到等价稀疏系数矩阵线性方程组，
[0025][0026]
g、采用共轭梯度法求解步骤f得到的稀疏线性方程组，并对解向量进行小波逆变换，得到展开系数向量c，最终获得
[0027]
进一步地，所述步骤e，包括以下步骤：
[0028]
e1、根据mallat塔式分解算法，相邻子空间中小波系数和尺度系数有递推关系：
[0029][0030]
其中，c
j-1
、cj、d
j-1
和dj分别为尺度空间v
j-1
和vj中的尺度系数和小波系数向量。h和g分别为低通滤波器和高通滤波器。
[0031]
e2、具有二阶消失矩的周期daubechie小波的低通滤波器hn表示为
[0032][0033]
其中hi为矩阵元素(i＝1,2,3,4)，高通滤波器gn与hn具有相同结构，由小波系数gk组成。
[0034]
e3、对于一个长度为n＝2n的向量s，它的周期小波分解可以通过n
×
n的矩阵来表示，
[0035][0036]
其中，hn和gn为n/2
×
n阶矩阵，分别称为低通滤波器和高通滤波器。一阶小波分解：
[0037]
wns＝[hns,gns]
t
ꢀꢀꢀ
(8)
[0038]
e4、重复小波分解步骤e3，得到向量s的离散小波变换，
[0039]
ws＝w
n-l
…wn-1
wns
ꢀꢀꢀ
(9)
[0040]
构造的离散小波变换矩阵w为一系列正交矩阵的乘积，所以w也是正交的。
[0041]
与现有技术相比，本发明的有益效果是：
[0042]
本发明提出一种离散小波矩量法求解lippermann-schwinger积分方程的快速数值方法。根据mallat塔式分解算法构造正交小波变换矩阵对矩量法形成的系数矩阵进行小波变换，使得变换后的系数矩阵为近似对角分布的稀疏矩阵，达到降低存储和计算复杂度的目的。
[0043]
本发明有以下优点：
[0044]
1、本发明选取具有较好消失矩、正则性和紧支撑的daubechie小波函数，利用mallat塔式分解算法得到daubechie小波滤波器，进而构造出正交小波变换矩阵对矩量法生成的系数矩阵进行稀疏化，降低了存储和计算复杂度，提高了矩量法在地震散射波场数值计算的计算效率；
[0045]
2、通过采用离散正交小波变换，可以将具有良好特性但没有显示表达式的小波函数(如daubechies小波函数族)直接应用于矩量法中；
[0046]
3、本发明避免了直接用小波基展开待求波场时，核函数与小波基函数复杂的内积积分计算；更换小波基函数时，本发明提出的离散小波矩量法，只需重新构造正交小波变换矩阵，无需重新计算基函数与核函数的内积积分。
附图说明
[0047]
为了更清楚地说明本发明实施例的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。
[0048]
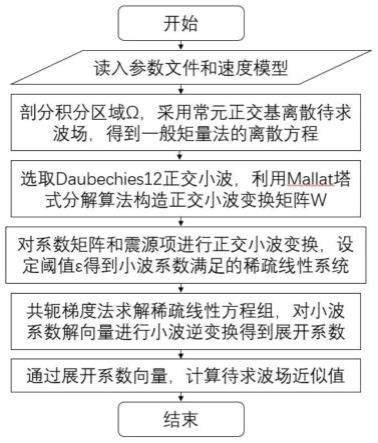
图1本发明总体流程图；
[0049]
图2数值模拟速度模型；
[0050]
图3阈值ε1＝1.0
×
10-6
的稀疏变换矩阵；
[0051]
图4阈值ε2＝1.0
×
10-5
的稀疏变换矩阵；
[0052]
图5阈值ε3＝1.0
×
10-4
的稀疏变换矩阵；
[0053]
图6阈值ε1＝1.0
×
10-6
稀疏变换矩阵的三维显示图；
[0054]
图7有限差分数值模拟结果；
[0055]
图8离散小波矩量法数值模拟结果。
具体实施方式
[0056]
下面结合实施例对本发明作进一步说明：
[0057]
下面结合附图和实施例对本发明作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释本发明，而非对本发明的限定。另外还需要说明的是，为了便于描述，附图中仅示出了与本发明相关的部分而非全部结构。
[0058]
应注意到：相似的标号和字母在下面的附图中表示类似项，因此，一旦某一项在一
个附图中被定义，则在随后的附图中不需要对其进行进一步定义和解释。同时，在本发明的描述中，术语“第一”、“第二”等仅用于区分描述，而不能理解为指示或暗示相对重要性。
[0059]
本发明离散小波矩量法是先利用一般的基函数将函数展开，通过矩量法得到常用的矩阵方程，再利用mallat塔式分解算法对矩阵方程进行正交小波变换求得展开系数。离散小波矩量法只需对矩量法形成的矩量矩阵进行变换，再利用稀疏化的矩阵求解。它是一种矩阵的运算，与连续算子方程关系不大，所以公式推导相对简单。与连续小波矩量法比，避免了小波基函数的直接积分。
[0060]
本发明基于离散小波矩量法的地震散射波场数值模拟方法，包括以下步骤：
[0061]
a、读入速度模型(模型大小nx*nz)，设置震源子波、背景速度。
[0062]
b、对积分区域ω进行均匀剖分(vj为第j个剖分面元)，取分片常函数空间构造标准正交基函数，满足
[0063][0064]
c、根据步骤b的正交分域基函数，对以速度扰动为权的位移场进行展开得到近似算子方程：
[0065][0066]
其中，en是映l2(ω)到sn的正投影算子。为带权总位移场，为带权背景场，k0＝ω/c为背景波数(c为常速背景介质速度)，α＝α(r)＝c2/v2(r)-1(v(r)为介质速度)，g＝g(r,r')为背景介质格林函数。
[0067]
d、选取步骤b中的分域基函数作为矩量法的权函数。利用正投影算子的自共轭性质，方程两边同时与权函数作内积，
[0068][0069]
其中，(
·
，
·
)表示l2(ω)的内积。由此，通过矩量法得到系数{cj,j＝1,
…
,n}满足线性方程组
[0070]g′
c＝s
ꢀꢀꢀ
(4)
[0071]
其中，且
[0072]
e、根据mallat塔式分解算法，相邻子空间中小波系数和尺度系数有递推关系：
[0073]
[0074]
其中，c
j-1
、cj、d
j-1
和dj分别为尺度空间v
j-1
和vj中的尺度系数和小波系数向量。h和g分别为低通滤波器和高通滤波器。
[0075]
具有二阶消失矩的周期daubechie小波的低通滤波器hn表示为
[0076][0077]
其中hi为矩阵元素(i＝1,2,3,4)，高通滤波器gn与hn具有相同结构，由小波系数gk组成。
[0078]
对于一个长度为n＝2n的向量s，它的周期小波分解可以通过n
×
n的矩阵来表示，
[0079][0080]
其中，hn和gn为n/2
×
n阶矩阵，分别称为低通滤波器和高通滤波器。一阶小波分解：
[0081]
wns＝[hns,gns]
t
ꢀꢀꢀ
(8)
[0082]
重复小波分解式(8)，得到向量s的离散小波变换，即选取daubechie小波函数，利用mallat塔式分解算法，通过daubechie小波滤波器构造出任意向量的正交小波变换矩阵w，
[0083]
ws＝w
n-l
…wn-1
wns，其中
[0084]
f、用步骤e得到的正交小波变换矩阵w对步骤d得到的系数矩阵进行小波变换，变换过程如下：
[0085][0086]
根据小波函数的紧支撑性、高阶消失矩特性，变换后矩阵中大部分小波系数为零或者值很小。设定阈值ε，在不影响计算精度的前提下忽略掉小于ε的值。采用一维索引只存储稀疏矩阵的非零元素可以降低内存。进而得到等价稀疏系数矩阵线性方程组，
[0087][0088]
g、采用共轭梯度法求解步骤f得到的稀疏线性方程组，并对解向量进行小波逆变换，得到展开系数向量c，最终获得
[0089]
为了更好的对上述具体算法流程的实施效果进行说明，下面给出一套具体实例：
[0090]
实施例1
[0091]
本发明基于离散小波矩量法的地震散射波场数值模拟方法整体流程，如图1所示。
[0092]
a、读入速度模型(图2)。模型大小为640m*640m，震源子波为主频15hz的雷克子波，背景速度为c＝3000m/s。
[0093]
b、对积分区域ω进行均匀剖分，构造标准正交基函数。
[0094]
c、根据步骤b的正交分域基函数，构造得到近似算子方程。
[0095]
d、选取步骤b中的分域基函数作为矩量法的权函数。利用正投影算子的自共轭性质，方程两边同时与权函数作内积，得到矩量法系数矩阵。
[0096]
e、根据mallat塔式分解算法，选取daubechie小波函数，利用mallat塔式分解算法，通过daubechie小波滤波器构造出任意向量的正交小波变换矩阵w。本实例中选取daub12小波函数。
[0097]
f、用步骤e得到的正交小波变换矩阵w对步骤d得到的系数矩阵进行小波变换。设定阈值ε，在不影响计算精度的前提下忽略掉小于ε的值。本示例中设定不同阈值并对正交小波变换后的矩阵进行显示。图3、图4和图5分别为设定阈值ε1＝1.0
×
10-6
、ε2＝1.0
×
10-5
、ε3＝1.0
×
10-4
。图6为阈值ε1的矩阵三维显示。可以看出，经过小波矩阵变换之后系数矩阵已变成带状稀疏矩阵，可以大大降低存储空间。
[0098]
g、采用以为索引存储小波变换后的稀疏矩阵，求解步骤f得到的稀疏线性方程组，并对解向量进行小波逆变换，得到展开系数向量c，最终获得待求波场。
[0099]
本实例中与有限差分正演模拟结果(图7)对比，采用离散小波矩量法得到的计算结果(图8)并没有损失计算精度。本发明中提出的离散小波矩量法可进一步应用于地震散射波偏移成像和全波形反演中，用于计算全波场的偏移格林函数和正反演格林函数。
[0100]
注意，上述仅为本发明的较佳实施例及所运用技术原理。本领域技术人员会理解，本发明不限于这里所述的特定实施例，对本领域技术人员来说能够进行各种明显的变化、重新调整和替代而不会脱离本发明的保护范围。因此，虽然通过以上实施例对本发明进行了较为详细的说明，但是本发明不仅仅限于以上实施例，在不脱离本发明构思的情况下，还可以包括更多其他等效实施例，而本发明的范围由所附的权利要求范围决定。