一种设计基于事件触发的磁悬浮系统模糊控制器的方法与流程

本发明应用于非线性系统的模糊控制，具体涉及一种设计基于事件触发的磁悬浮系统模糊控制器的方法。

背景技术：

磁悬浮系统由于其环境、商业和技术等方面的特点，在许多实际生产应用中得到广泛的应用。ems系统的磁悬浮列车是当今非常先进的轨道交通工具。ems系统利用电磁力来克服重力，利用“同性相斥，异性相吸”的原理，使得磁悬浮列车以一定的间隙浮于轨道上方，使其完全脱离轨道。磁悬浮列车在正常运行状态中需要控制稳定的电流，以保证列车的正常悬浮以及高速安全行驶，因此磁悬浮列车电流控制技术是十分重要的。由于有电磁力的参与，典型的磁悬浮系统是高度非线性、开环不稳定的系统。

传统的控制方法都是以建立被控对象的精确模型为基础进行控制。但随着被研究系统的复杂性的增加，有时难以建立起精确模型，有时所研究的对象具有强非线性、时滞、时变、外部干扰等复杂情况，利用现在的数学方法难以求解计算，传统控制方法就不再适应。

在实际磁悬浮系统中，由于传感器、执行机构和所设计的控制器都是作为节点与列车的控制系统相连，并通过网络进行数据交换，因为网络的带宽有限，容易导致信息碰撞而产生输入诱导时延，可能会导致所控制的系统不稳定。

技术实现要素：

目前对磁悬浮系统的控制研究大都是将磁悬浮模型在平衡点进行泰勒展开，从而得到线性化的模型，但该方法对于存在时变时延、数据碰撞丢失等情况的时候并不适用。因此，本发明针对复杂的非线性磁悬浮系统的控制，解决诱导时延，减少不必要的数据传输，节约有限带宽的资源，提供了一种设计基于事件触发的磁悬浮系统模糊控制器的方法。

为了解决上述技术问题，本发明采用了如下技术方案：

一种设计基于事件触发的磁悬浮系统模糊控制器的方法，该方法包括如下步骤:

1、建立非线性磁悬浮系统的动态模型，通过在平衡点展开再转换成状态空间方程，通过4个模糊规则对磁悬浮系统进行t-s模糊建模；

2、利用事件触发策略，以及模糊控制器，得到相应的基于事件触发的磁悬浮闭环模糊系统；

3、利用交互凸组合的方法以及融合参数依赖的李雅普诺夫函数，推导出稳定性条件以及设计对应的基于事件触发的模糊控制器，并用线性矩阵不等式(lmi)表示，便于用matlab求解。

与现有技术相比，本发明具有如下技术效果：

1、本发明设计出对于非线性磁悬浮系统的事件触发模糊控制器，即使在传感器、执行机构、所设计的控制器与控制系统进行信息数据交换发生碰撞，而产生诱导时延时，还是能够通过事件触发模糊控制器的控制下保持系统的性能以及稳定性。

2、本发明能对非线性磁悬浮系统进行有效控制，使得其在运行的时候是稳定的，并且能减少不必要的信息传输，节约带宽资源。

附图说明

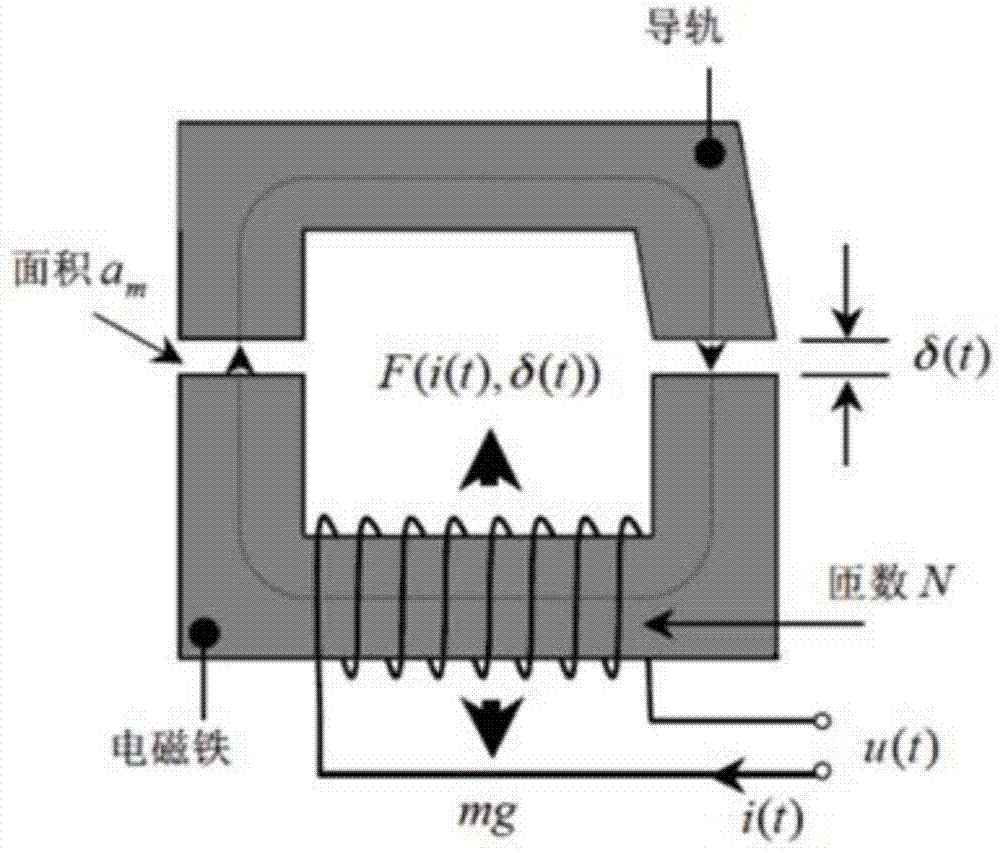
图1为磁悬浮列车的结构简化图；

图2为基于事件触发的模糊控制系统图；

图3为原磁悬浮开环系统的状态轨迹图；

图4为受控的闭环模糊系统的状态轨迹图；

图5为事件触发时刻以及时间间隔图；

图6为模糊控制器的输入图。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细地描述。

一种设计基于事件触发的磁悬浮系统模糊控制器的方法，该方法包括如下步骤:

1)建立非线性磁悬浮系统的动态模型，通过在平衡点展开再转换成状态空间方程，通过4个模糊规则对磁悬浮系统进行t-s模糊建模；

2)利用事件触发策略，以及模糊控制器，得到相应的基于事件触发的磁悬浮闭环模糊系统；

3)利用交互凸组合的方法以及融合参数依赖的李雅普诺夫函数，推导出稳定性条件以及设计对应的基于事件触发的模糊控制器，并用线性矩阵不等式(lmi)表示，便于用matlab求解。

下面主要对磁悬浮系统模糊模型建模、基于事件触发的闭环模糊系统构建以及模糊控制器设计方法进行描述，以解决非线性磁悬浮系统的基于事件触发模糊控制器设计的问题。

图1给出了磁悬浮列车的结构简化图，根据牛顿定理以及基尔霍夫定理，对磁悬浮系统进行物理分析。在步骤1)的建模过程中，不考虑轨道本身的形变对系统模型的影响，仅考虑电磁铁相对于轨道的运动关系，根据牛顿定理以及基尔霍夫定理，可以求得磁悬浮系统的动态描述方程如下：

其中，ψ(i(t),δ(t))是系统的磁势，f(i(t),δ(t))表示电磁铁产生的电磁力，μ0为真空磁导率(4π×10^-7h/m)，g是重力加速度(9.8m/s²)，n是线圈匝数，m是电磁铁以及客厢总重，rm是线圈电阻，am是线圈绕组有效横截面积，δ(t)是电磁铁与导轨之间的空气隙，i(t)是控制线圈电流，v(t)是控制线圈两端电压；

将式(1)中的等式经过简单的代入数学变化，可以得到下式的结果：

选取系统的状态z1＝δ(t)，以及z3＝i(t)，那么，式(2)可以转换成如下的状态空间表达：

因为在系统正常运行状态下，系统始终是处于稳定的状态，设z1＝δ(t)的稳定状态为z1e＝δref，则相应的的稳定状态为z2e＝0，z3＝i(t)的稳定状态是

其中，δref是状态z1的平衡态，是对状态z1求导，是状态z2求导，是状态z3求导；

为了便于下面的分析，将做如下的变换：

式中，x(t)是状态变量矩阵[x1^t(t)x2^t(t)x3^t(t)]^t，x1(t)是z1(t)-z1e的等价变换，x2(t)是z2(t)的等价变换，x3(t)是z3(t)-z3e的等价变换；

令u(t)＝v(t)-ve，将上式(4)代入到式(3)中，容易得到下面的对应的系统状态空间方程：

式中，u(t)是v(t)-ve的等价变换，ve是输入变量的平衡态，是对状态变量x1(t)求导，是对状态变量x2(t)求导，是对状态变量x3(t)求导；

由式(5)所得到的系统状态空间方程是高度非线性的，无法用现存的线性控制方法以及经典控制来处理该系统。为了能利用线性控制方法，接下来利用基于t-s模糊模型来逼近该非线性系统；

利用t-s模糊建模来逼近原非线性系统时，定义即可得到如下结果：

则θ1(t)和θ2(t)可表示为如下的形式：

其中

ξ11(θ1(t))+ξ12(θ1(t))＝1；ξ21(θ2(t))+ξ22(θ2(t))＝1(8)

式中，θ1(t)是前件变量x1(t)，θ2(t)是前件变量x3(t)，θ1max是前件变量x1(t)的最大值，θ2max是前件变量x3(t)的最大值，ξ11(θ1(t))是前件变量θ1(t)的隶属度函数，ξ12(θ1(t))是前件变量θ1(t)的隶属度函数，ξ21(θ2(t))是前件变量θ2(t)的隶属度函数，ξ22(θ2(t))是前件变量θ2(t)的隶属度函数；

磁悬浮系统在正常运行状态，导轨之间的空气隙δ(t)，将x1(t)定义为系统的输出，即y(t)＝x1(t)，那么，就可以用如下的4条模糊规则来等效于原系统；

模糊规则1：当θ1(t)接近θ1max，θ2(t)接近θ2max时，该非线性等式可化简为：

模糊规则2：当θ1(t)接近θ1max，θ2(t)接近θ2min时，该非线性等式可化简为：

模糊规则3：当θ1(t)接近θ1min，θ2(t)接近θ2max时，该非线性等式可化简为：

模糊规则4：当θ1(t)接近θ1min，θ2(t)接近θ2min时，该非线性等式可化简为：

式中，y(t)含义是系统的连续输出；

利用一阶欧拉近似的方法，将该磁悬浮连续模型离散化，从而可以得到如下的离散的t-s模糊模型：

模糊规则1：当θ1(t)是m11，θ2(t)是m12时，则该非线性等式可化简为：

模糊规则2：当θ1(t)是m21，θ2(t)是m22时，则该非线性等式可化简为：

模糊规则3：当θ1(t)是m31，θ2(t)是m32时，则该非线性等式可化简为：

模糊规则4：当θ1(t)是m41，θ2(t)是m42时，则该非线性等式可化简为：

其中，m11和m21都表示接近θ1max；m31和m41都表示接近θ1min；m12和m32都表示接近θ2max；m22和m42都表示接近θ2min，x(k+1)是系统状态变量的下一时刻状态，x(k)是系统状态变量矩阵，u(k)是系统输入，y(k)是系统的离散输出，a1、b1、c1均表示模糊规则1下的系统矩阵，a2、b2、c2均表示模糊规则2下的系统矩阵，a3、b3、c3均表示模糊规则3下的系统矩阵，a4、b4、c4均表示模糊规则4下的系统矩阵；t表示采样时间；所以，mij的隶属度函数表示如下式，i∈{1,2,3,4}，j∈{1,2}；

m11(θ1(k))＝m21(θ1(k))＝ξ11(θ1(k)),m31(θ1(k))＝m41(θ1(k))＝ξ12(θ1(k))

m12(θ2(k))＝m32(θ2(k))＝ξ21(θ2(k)),m22(θ2(k))＝m42(θ2(k))＝ξ22(θ2(k))

式中，θ1(t)是前件变量x1(t)，θ2(t)是前件变量x3(t)；

去模糊化t-s模糊模型表示为：

其中：θ(k)是前件变量，hi是模糊基底函数，ai、bi、ci是模糊规则1，2，3，4下的模糊系统的系统矩阵；

h1(θ(k))＝ξ11(θ1(k))·ξ12(θ1(k)),h2(θ(k))＝ξ11(θ1(k))·ξ22(θ1(k))

h3(θ(k))＝ξ21(θ1(k))·ξ12(θ1(k)),h4(θ(k))＝ξ21(θ1(k))·ξ22(θ1(k))

其中，h1是模糊规则1下的模糊基底函数，h2是模糊规则2下的模糊基底函数，h3是模糊规则3下的模糊基底函数，h4是模糊规则4下的模糊基底函数；

上述模型可以表达为下式的紧凑形式：

其中：a(k)、b(k)、c(k)是模糊规则下系统矩阵的紧凑形式，具体表达形式如下：

在步骤2)获得基于事件触发的闭环模糊系统过程中：引入一种机制来决定是否传输“信息”，且保证该传输的信息确实对系统的稳定运行来说是必不可少的，从而可以很大程度上减少传输的信息的量。为了减少不必要的数据传输以及节约网络带宽资源，利用事件触发策略来决定系统的状态x(k)是否该传送；

2.1)事件触发决策算法：

[x(k)-x(kt)]^tω[x(k)-x(kt)]≤σx^t(kt)ωx(kt)(12)

其中：ω是需要求的对称正定矩阵，σ是给定的参数σ∈[0,1)，该不等式即表示，对于系统状态x(k)满足式子(12)不会被传送；最新的采样状态是否会被传输取决于在触发kt时刻的最新的传输数据x(kt)与当前采样k时刻的数据x(k)是否满足上述式子；

2.2)基于事件触发的模糊控制系统如图2所示。

模糊规则i，模糊规则i统一代表模糊规则1，2，3，4；

如果θ1(k)是mi1，θ2(k)是mi2，那么

u(k)＝kix(k),i∈1,2,3,4(13)

其中，ki是要求得的模糊控制器的增益矩阵，因此，又可以表示为

则

u(k)＝k(k)x(k)(15)

其中，

假设网络诱导延时满足其中τ和分别表示时变时延的最小值和最大值；以下，考虑两种事件触发的情况：

情况1：如果定义h(k)如下：

h(k)＝k＝kt,k∈[kt+τk,kt+1+τk+1]

显然：

情况2：如果那么，考虑如下的两个区间：

其中：n∈n,n≥1；

因为总是成立的，那么，总是存在d使得并且，x(kt)和x(kt+n)满足式子(12)；

定义如下式子：

其中，n＝1,2,3,...,d-1；因此，可以得到以下的式子：

定义h(k)如下：

因此，可得：

令由上述分析，显然可以得到

令h＝h2-h1；

对于情况1，定义ei(k)＝0，

对于情况2，定义：

通过上述两种情况的分析，结合ei(k)的定义以及事件触发策略算法式(12)，对于

式(12)可重写为如下形式：

ei(k)^tωei(k)≤σx^t(k-h(k))ωx(k-h(k))(18)

利用ei(k)和h(k)，对应的模糊控制器为

u＝kx(k)＝ke(k)+kx(k-h(k))(19)

将式子(19)代入到式子(11)，可得到对应的磁悬浮闭环系统表示为：

在步骤3)基于事件触发的模糊控制器设计中包括如下子步骤：

3.1)稳定性分析

在进行稳定性分析之间，定义如下的参数矩阵：

3.1.1)对于给定的标量σ，h1，h2，并且已知系统的控制增益k；则该闭环系统(20)是渐进稳定的的条件是：存在矩阵q1i＞0，q2i＞0，q3i＞0，s1＞0,s2＞0,ω＞0,m,z1对于正数k满足：

υ(k)+υ1(k)＜0(21)

其中：

wa＝[a(k)0b(k)k0b(k)k-in]

w1＝[i00000]w2＝[0i0000]

w3＝[00i000]w4＝[000i00]

w5＝[0000i0]w6＝[00000i]

其中，in是n×n的单位矩阵，*是对称矩阵的对称项，上角标“t”代表矩阵转置；

3.1.1)得到的结果是模糊参数依赖矩阵不等式的形式，无法用lmi工具箱直接求解。所以需要将此结果转换为有限的线性矩阵不等式，并可以利用标准的工具箱进行求解。下面的定理就是将这些矩阵约束转换为有限的线性矩阵不等式；

3.2.2)对于给定的标量σ，h1，h2，并且已知系统(20)的控制增益ki；则该闭环系统是渐进稳定的条件是：存在矩阵q1i＞0，q2i＞0，q3i＞0，s1＞0,s2＞0,ω＞0,mi(k),z1对于正数k满足下式，其中i,j,k,s＝1,2,3,4：

υiis(k)+υ1iis(k)＜0(23)

υijs(k)+υ1ijs(k)+υjis(k)+υ1jis(k)＜0，1≤i＜j(24)

其中：

wajs＝[aj0bjks0bjks-in]；

3.2)对步骤3.1)的结果，来设计模糊系统(20)的基于事件触发的模糊控制器，使得磁悬浮模糊系统是渐进稳定的。

对于给定的标量σ，h1，h2，λ1，λ2，...，λ6；该闭环系统的基于事件触发的模糊控制器存在，且满足磁悬浮系统是渐进稳定的条件是：存在矩阵φi,x对于正数k满足下式，其中i,j,k,s＝1,2,3,4：

πiis(k)+π1iis(k)＜0(26)

πijs(k)+π1ijs(k)+πjis(k)+π1jis(k)＜0，1≤i＜j(27)

其中：

并且该模糊系统的反馈增益矩阵可由下式计算得到：

ki＝φix^-1。

至此，完成了基于事件触发策略的非线性磁悬浮系统的模糊控制器设计。

实施例1

利用对磁悬浮非线性系统所设计的基于事件触发的模糊控状态反馈制器进行仿真。下表1列出了磁悬浮系统中的相应的参数，在下表2中列出了前件变量θ(k)的所允许的取值范围。

表1磁悬浮非线性系统参数量值

表2前件变量θ(k)所允许的范围

利用表1和表2中的参数值，可以得到原磁悬浮非线性系统的确切的表达式。在求解模糊控制器之前，先分析原磁悬浮非线性系统的稳定性。首先，假设该系统的状态初始条件为x(0)＝[0.000100]^t。图3给出了原磁悬浮开环系统的状态轨迹图。

从图3可以看出，非线性磁悬浮在不受控的情况下状态轨迹是发散的，系统是不稳定的。

利用matlab中进行求解，可得该非线性磁悬浮系统的基于事件触发的模糊控制器的参数矩阵：

k1＝10³×[-9.48230.12140.0216],k2＝10⁴×[-5.24210.09290.0118]

k3＝10⁴×[7.7503-0.1409-0.0177],k4＝10³×[2.6740-0.0445-0.0060]

事件触发参数矩阵ω求解如下：

根据以上的求解，可得到系统的基于事件触发的非线性磁悬浮系统的模糊控制器，图4表示的是在该控制器下，系统的状态轨迹图。从该图4中可以看出该非线性磁悬浮系统在模糊控制下的状态轨迹是收敛的，已被镇定。

图5表示的事件触发的时刻以及间隔时间，图6为模糊控制器的输入，从图5、图6中可见，利用事件触发策略可以有效减少通信的负担。

最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。