一种基于有限时间稳定的对称组合大系统的分散控制方法

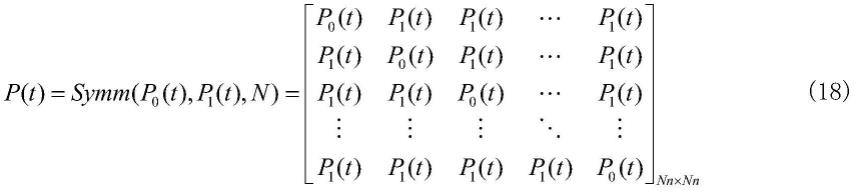
1.本发明属于控制工程技术领域，尤其是涉及一种基于有限时间稳定的对称组合大系统的分散控制方法。


背景技术：

2.随着社会的不断发展，人们在日常生活中接触到越来越多的大型系统，其系统信息量庞大、结构繁琐、影响因素多样的特点也给控制理论的研究带来许多挑战。在大系统的研究过程中，对称组合系统作为一类特殊的大系统，因其对称的结构在工业领域分布广泛。对于此类系统，采用集中控制将使得整个控制系统信息交换异常复杂，在系统维数较大的时候导致运行成本提高，系统的可靠性降低。针对这些问题，20世纪70年代出现分散控制方法，分散控制相比于集中控制；首先，各子系统具有针对各自特性的控制器，提高控制效率及控制质量；其次，子系统间无需进行信息交换，增加系统控制器设计的简便性；最后，即使某一子系统故障，其余子系统仍能正常运行，增加系统的可靠性。
3.大系统的稳定性分析与综合问题一直是系统控制理论研究中的重点。在稳定性问题的研究方法中，最为著名的是lyapunov稳定性理论。20世纪90年代末，已有许多学者对对称组合大系统的稳定性进行研究，其中大部分成果是基于lyapunov理论背景得出的。但lyapunov稳定性理论更偏向研究系统的渐近稳定性，而在工业生产的过程中，人们更关心系统在短时间内的暂态表现。因此，有限时间稳定的控制方法应运而生，其保证系统在某一确定的(短时间或暂态)时间范围内，系统状态的幅度始终在规定的轨迹域内。
4.有限时间稳定相关概念的出现最早可以追溯到20世纪60年代，一经提出便得到引起许多学者的关注，得到许多有限时间稳定框架下的研究成果。受当时计算手段与运算工具的限制，即使推导出有效有限时间镇定控制器设计方法，却仍然难以通过计算实现。直至上个世纪90年代，线性矩阵不等式工具箱的出现，使得有限时间稳定理论能够应用在工程中，才又激发起学者们新一轮的研究热情，将有限时间稳定理论进一步推广到非线性系统、随机系统、自适应系统等领域。
5.迄今为止，有限时间控制理论与各类系统结合，解决众多系统分析以及控制器设计问题，有限时间稳定理论已经成为控制理论中不可或缺的一部分。然而在有限时间稳定理论中，针对大系统的相关文献仍然较少，关于大系统的有限时间分散控制器设计相关的研究仍然是空白。


技术实现要素：

6.本发明的目的在于针对现有技术存在的上述空白，提供利用大系统的相似结构简化有限时间稳定分析综合过程，解决对称组合系统的有限时间稳定性分析和有限时间镇定问题,利用线性矩阵不等式或微分线性矩阵不等式对有限时间稳定条件和有限时间稳定控制器设计策略进行描述的一种基于有限时间稳定的对称组合大系统的分散控制方法。
7.本发明包括以下步骤：
8.步骤1，确定一个对称组合大系统：
[0009][0010]
其中xi(t)∈rn，ui(t)∈rm，yi(t)∈r
p
分别为系统的状态量、控制输入量与控制输出量。
[0011]
步骤2，对步骤1所述对称组合系统，进行等价描述：
[0012][0013]
其中,且矩阵a∈r
nn
×
nn
,b∈r
nn
×
nm
,c∈r
np
×
nn
有如下形式：
[0014][0015]
b＝block-diag{b0,b0,
…
,b0},c＝block-diag{c0,c0,
…
,c0}。其中block-diag(*)表示以*为主对角线元素构成的分块对角矩阵；
[0016]
符号symm(x,y,r)表示如下r
×
r维的矩阵：
[0017][0018]
其中，x和y为具有相同维度的方阵；利用此形式，将系统矩阵a表示为a＝symm(a0,h,n)；系统(2)称为对称组合系统，是由n个相同的子系统通过相似的内联形式组合而成的复合系统；
[0019]
步骤3，引入含有子系统和互联项信息的低维系统，并建立假设；对于系统(2)，取a
p
＝a0+(n-1)h且am＝a
0-h；给定正定矩阵r0∈rn×n，一个定义在区间[t0,t0+t]上的正定矩阵值函数γ0(
·
)∈r
nn
×
nn
，其满足γ0(t0)＜r0，同时令r＝block-diag{r0,r0,
…
,r0}，r∈r
nn
×
nn
且γ(t)＝block-diag{γ0(t),γ0(t),
…
,γ0(t)}，γ∈r
nn
×
nn
；
[0020]
步骤4，根据有限时间稳定定义，应用两个引理，提出对称组合系统有限时间稳定简化分析定理。
[0021]
步骤5，根据步骤4所述简化分析定理，进一步提出基于状态反馈构建有限时间分散控制器设计方法，实现对称组合系统有限时间稳定分散控制。
[0022]
在步骤4中，所述两个引理分别为：
[0023]
引理1：下述两个条件是等价的：
[0024]
(1)时变系统x(t0)＝x0关于(t0,t,r0,γ0(
·
))有限时间稳定；
[0025]
(2)下述带有初始条件和终端条件的微分线性矩阵不等式
[0026]
[0027]
p(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0028]
p(t0)＜r0.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0029]
在t∈[t0,t0+t]上有分段连续可微对称解p(
·
)。
[0030]
引理2：考虑线性时不变系统：
[0031][0032]
给定一个正标量t以及正定矩阵r0∈rn×n，若存在一个非负标量α和正定矩阵p∈rn×n使得
[0033][0034][0035]
成立，其中表示p的条件数，系统(8)关于(t,r0,ρr0)，0＜ρ＜1有限时间稳定。
[0036]
注意到当非负标量α的取值确定后，条件(9)即转变为一个传统的线性矩阵不等式约束。进一步地，式(10)也可以由如下形式的线性矩阵不等式确保其可行性：
[0037]
ρe
αt
i＜p＜i.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0038]
结合式(9)以及(11)，给出一个基于线性矩阵不等式的线性时不变系统有限时间稳定判据。
[0039]
注1：一方面，若条件(9)中α取值为0时，对比连续系统lyapunov方程，易得系统(8)是渐近稳定的，且对于所有t∈(0,+∞)均有x
t
(t)ρr0x(t)＜1。另一方面，若条件(9)中α取值为0且条件(10)中α不取为0，则系统(8)在满足渐近稳定的同时，也关于(t,r0,ρr0)有限时间稳定。
[0040]
在步骤4中，有限时间稳定简化分析定理为：
[0041]
定理1：若两个n维系统和关于(t0,t,r0,γ0(
·
))有限时间稳定，那么对称组合系统(2)是关于(t0,t,r,γ(
·
))有限时间稳定的。
[0042]
证明：由引理1可知，若低维系统和均关于(t0,t,r0,γ0(
·
))有限时间稳定，等价于存在定义在[t0,t0+t]上的分段连续可微对称矩阵p
p
(
·
)和pm(
·
)使得下列两组带有初始条件与终端条件的微分线性矩阵不等式成立，
[0043][0044]
p
p
(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0045]
p
p
(t0)＜r0.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0046]
与
[0047][0048]
pm(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0049]
pm(t0)＜r0.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0050]
令p0(t)＝[p
p
(t)+(n-1)pm(t)]/n，p1＝[p
p
(t)-pm(t)]/n，构建如下形式的矩阵值
函数p(t)，
[0051][0052]
根据p
p
(t)以及pm(t)的分段连续可微特性，易知经线性组合后的p0(t)和p1(t)以及构建的函数p(t)同样是分段连续对称可微的，再取如下变换矩阵：
[0053][0054]
其中，i∈rn×n为单位矩阵，经计算后可得到如下结果：
[0055][0056]
观察式(20)易得其为上三角矩阵，对于观察式(20)易得其为上三角矩阵，对于其中指pm(t)-γ0(t)的特征值重复n-1次。再由式(13)和(16)可得在区间t∈[t0,t0+t]上有p
p
(t)-γ0(t)＞0和pm(t)-γ0(t)＞0，进一步有λ
min
(p
p
(t)-γ0(t))＞0和λ
min
(pm(t)-γ0(t))＞0，其中λ
min
(*)表示矩阵“*”的最小特征值。再结合式(20)，可知λ
min
(ξ(p(t)-γ(t)ξ-1
))＝λ
min
(p(t)-γ(t))＞0，即对于均有p(t)＞γ(t)。同理，由式(14)以及(17)可推知p(t0)＜r。
[0057]
此外，令经计算后可得
[0058][0059]
其中
[0060]
[0061]
又由式(12)以及式(15)可知对于均有λ
max
(ξσ(t)ξ-1
)＝λ
max
(σ(t))＜0，其中λ
max
(*)表示矩阵“*”的最大特征值，即可推知σ(t)＜0，综上，可知对称组合系统是关于(t0,t,r,γ(
·
))有限时间稳定的。定理得证。
[0062]
所述步骤5中连续对称组合系统的状态反馈分散镇定控制器设计问题描述如下：
[0063]
问题1：考虑系统(2)，给定正定矩阵r＝block-diag{r0,
…
,r0}，正标量t，初始时间t0，定义在[t0,t0+t]上的正定矩阵值函数γ(
·
)＝block-diag{γ0(
·
),
…
,γ0(
·
)}，满足γ0(t0)＜r0，设计如下形式的状态反馈控制器
[0064]
ui(t)＝ki(t)xi(t),i＝1,
…
,n,
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22)
[0065]
使系统
[0066][0067]
关于(t0,t,r,γ(
·
))有限时间稳定，其中k(t)＝block-diag{k1(t),
…
,kn(t)}。
[0068]
提出如下定理解决问题1，设计有限时间状态反馈分散控制器：
[0069]
定理2：若存在分段连续可微矩阵值函数q(
·
)∈rn×n以及连续矩阵值函数l(
·
)∈rm×n满足如下带有初始条件和终端条件的微分线性矩阵不等式组
[0070][0071][0072][0073][0074]
那么此时系统有限时间状态反馈分散镇定控制器增益为：
[0075]ki
(t)＝l(t)q-1
(t):＝k0(t),i＝1,
…
,n.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(28)
[0076]
证明：
[0077]
不妨令且那么式(24)和式(25)可分别转化成如下形式：
[0078][0079][0080]
取p(t)＝q-1
(t)，并用p(t)同时左乘和右乘式(26)、(27)、(29)以及(30)，计算后可得
[0081][0082][0083]
p(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(33)
[0084]
p(t)＜r0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(34)
[0085]
利用引理所得结论可知，系统和均关于(t0,t,r0,γ0(
·
))有限时间稳定。进一步地，再利用定理1结论可得，系统关于(t0,t,r,γ(
·
))有限时
间稳定。证明完毕。
[0086]
考虑定理2中q(t)的时变性给微分线性矩阵不等式组(24)-(27)的求解带来一定的难度。从实际的角度出发，更倾向于将问题转移到线性矩阵不等式的框架下进行求解。下面给出一个基于线性矩阵不等式的综合方法，将矩阵值函数γ(t)取为与矩阵r同形的常值矩阵，即令γ(t)＝γ＝ρr,0＜ρ＜1且初始时间t0＝0，在此条件下，对问题1进行重新描述如下。
[0087]
问题2：给定正标量t，正定矩阵r＝block-diag{r0,
…
,r0}，设计一个如式(22)形式的状态反馈分散控制器，使得闭环系统(23)关于(t,r,ρr)有限时间镇定。
[0088]
针对此问题，给出基于线性矩阵不等式的控制器设计方法。
[0089]
定理3：若存在非负标量α1和α2，正定矩阵q∈rn×n，矩阵m0∈rm×n，满足下述线性矩阵不等式组：
[0090][0091][0092][0093]
其中α＝max{α1,α2}。此时问题2有解，且此时分散状态反馈控制器增益为：
[0094][0095]
证明：
[0096]
由式(38)可解得将其代入式(35)和式(36)中可得
[0097][0098][0099]
取用同时左乘与右乘式(39)和式(40)，可得
[0100][0101][0102]
考虑到cond(p)＝cond(q)，易得i＝1,2。取和通过引理2结论，可知闭环系统和均关于(t,r0,ρr0)有限时间稳定。进一步由定理1结论可得，在线性矩阵不等式框架下，闭环系统是关于(t,r,ρr)有限时间稳定的。
[0103]
综上所述，通过状态反馈，能够对低维连续系统设计有限时间镇定控制器，且所得控制器通过分块对角形式可直接构建成连续对称组合系统的镇定控制器。
[0104]
本发明的主要目的在于：(1)针对现有技术的空白，提供一种大系统的有限时间分散控制方法，丰富大系统理论；(2)利用大系统的相似结构简化有限时间稳定分析综合过
程，解决对称组合系统的有限时间稳定性分析和有限时间镇定问题；(3)利用线性矩阵不等式或微分线性矩阵不等式对有限时间稳定条件和有限时间稳定控制器设计策略进行描述，更便于求解。
[0105]
本发明的有益效果是：
[0106]
1)针对一类对称组合大系统，研究其有限时间稳定性分析和有限时间镇定问题，填补大系统理论的空白；2)利用大系统的相似结构简化分析综合过程，减少计算复杂度；3)利用线性矩阵不等式或微分线性矩阵不等式对有限时间稳定条件和有限时间稳定控制器设计策略进行描述。
附图说明
[0107]
图1为验证本发明所采用的机械系统示意图。
[0108]
图2为采用本发明中有限时间分散控制器控制下系统状态的轨迹仿真曲线。
具体实施方式
[0109]
下面结合附图和具体实施方式对本发明进行详细说明。
[0110]
本发明针对一类具有对称结构的组合大系统的有限时间分散控制问题，基于有限时间稳定理论，得到对称组合大系统有限时间稳定的简化条件。根据简化条件设计状态反馈控制器和输出反馈控制器，并利用线性矩阵不等式或微分线性矩阵不等式对有限时间稳定条件和有限时间稳定控制器设计策略进行描述，更便于求解。
[0111]
步骤1，确定一个对称组合大系统：
[0112][0113]
其中xi(t)∈rn，ui(t)∈rm，yi(t)∈r
p
分别为系统的状态量、控制输入量与控制输出量。
[0114]
步骤2，对步骤1所述对称组合系统，进行等价描述：
[0115][0116]
其中且矩阵a∈r
nn
×
nn
,b∈r
nn
×
nm
,c∈r
np
×
nn
有如下形式：
[0117][0118]
b＝block-diag{b0,b0,
…
,b0},c＝block-diag{c0,c0,
…
,c0}。其中block-diag(*)表示以*为主对角线元素构成的分块对角矩阵。
[0119]
为简化表示，引入符号symm(x,y,r)表示如下r
×
r维的矩阵：
[0120][0121]
其中x和y为具有相同维度的方阵。利用此形式，可以将系统矩阵a表示为a＝symm(a0,h,n)。本文中，称系统(2)为对称组合系统，其是由n个相同的子系统通过相似的内联形式组合而成的复合系统。
[0122]
步骤3，引入含有子系统和互联项信息的低维系统，并建立假设。对于系统(2)，取a
p
＝a0+(n-1)h且am＝a
0-h。给定正定矩阵r0∈rn×n，一个定义在区间[t0,t0+t]上的正定矩阵值函数γ0(
·
)∈r
nn
×
nn
，其满足γ0(t0)＜r0，同时令r＝block-diag{r0,r0,
…
,r0}，r∈r
nn
×
nn
且γ(t)＝block-diag{γ0(t),γ0(t),
…
,γ0(t)}，γ∈r
nn
×
nn
。
[0123]
步骤4，根据有限时间稳定定义，应用两个引理，提出对称组合系统有限时间稳定简化分析定理。
[0124]
所述步骤4中的两个引理，分别为：
[0125]
引理1：下述两个条件是等价的：
[0126]
(1)时变系统有限时间稳定；
[0127]
(2)下述带有初始条件和终端条件的微分线性矩阵不等式
[0128][0129]
p(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0130]
p(t0)＜r0.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0131]
在t∈[t0,t0+t]上有分段连续可微对称解p(
·
)。
[0132]
引理2：考虑线性时不变系统
[0133][0134]
给定一个正标量t以及正定矩阵r0∈rn×n，若存在一个非负标量α和正定矩阵p∈rn×n使得
[0135][0136][0137]
成立，其中表示p的条件数，系统(8)关于(t,r0,ρr0)，0＜ρ＜1有限时间稳定。
[0138]
注意到当非负标量α的取值确定后，条件(9)即转变为一个传统的线性矩阵不等式约束。进一步地，式(10)也可以由如下形式的线性矩阵不等式确保其可行性：
[0139]
ρe
αt
i＜p＜i.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0140]
结合式(9)以及(11)，给出一个基于线性矩阵不等式的线性时不变系统有限时间稳定判据。
[0141]
注1：一方面，若条件(9)中α取值为0时，对比连续系统lyapunov方程，易得系统(8)是渐近稳定的，且对于所有t∈(0,+∞)均有x
t
(t)ρr0x(t)＜1。另一方面，若条件(9)中α取值为0且条件(10)中α不取为0，则系统(8)在满足渐近稳定的同时，也关于(t,r0,ρr0)有限时间稳定。
[0142]
所述步骤4中的有限时间稳定简化分析定理为：
[0143]
定理1：若两个n维系统和关于(t0,t,r0,γ0(
·
))有限时间稳定，那么对称组合系统(2)是关于(t0,t,r,γ(
·
))有限时间稳定的。
[0144]
证明：由引理1可知，若低维系统和均关于(t0,t,r0,γ0(
·
))有限时间稳定，等价于存在定义在[t0,t0+t]上的分段连续可微对称矩阵p
p
(
·
)和pm(
·
)使得下列两组带有初始条件与终端条件的微分线性矩阵不等式成立；
[0145][0146]
p
p
(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0147]
p
p
(t0)＜r0.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0148]
与
[0149][0150]
pm(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0151]
pm(t0)＜r0.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0152]
令p0(t)＝[p
p
(t)+(n-1)pm(t)]/n，p1＝[p
p
(t)-pm(t)]/n，构建如下形式的矩阵值函数p(t)，
[0153][0154]
根据p
p
(t)以及pm(t)的分段连续可微特性，易知经线性组合后的p0(t)和p1(t)以及构建的函数p(t)同样是分段连续对称可微的，再取如下变换矩阵：
[0155][0156]
其中i∈rn×n为单位矩阵，经计算后可得到如下结果：
[0157][0158]
观察式(20)易得其为上三角矩阵，对于为上三角矩阵，对于其中指pm(t)-γ0(t)的特征值重复n-1次。再由式(13)和(16)可得在区间t∈[t0,t0+t]上有p
p
(t)-γ0(t)＞0和pm(t)-γ0(t)＞0，进一步有λ
min
(p
p
(t)-γ0(t))＞0和λ
min
(pm(t)-γ0(t))＞0，其中λ
min
(*)表示矩阵“*”的最小特征值。再结合式(20)，可知λ
min
(ξ(p(t)-γ(t)ξ-1
))＝λ
min
(p(t)-γ(t))＞0，即对于均有p(t)＞γ(t)。同理，由式(14)以及(17)可推知p(t0)＜r。
[0159]
此外，令经计算后可得：
[0160][0161]
其中：
[0162][0163]
又由式(12)及式(15)可知对于均有λ
max
(ξσ(t)ξ-1
)＝λ
max
(σ(t))＜0，其中λ
max
(*)表示矩阵“*”的最大特征值，即可推知σ(t)＜0，综上，可知对称组合系统是关于(t0,t,r,γ(
·
))有限时间稳定的。定理得证。
[0164]
步骤5，根据步骤4所述简化分析定理，进一步提出基于状态反馈构建有限时间分散控制器设计方法，实现对称组合系统有限时间稳定分散控制。
[0165]
所述步骤5中连续对称组合系统的状态反馈分散镇定控制器设计问题描述如下：
[0166]
问题1：考虑系统(2)，给定正定矩阵r＝block-diag{r0,
…
,r0}，正标量t，初始时间t0，定义在[t0,t0+t]上的正定矩阵值函数γ(
·
)＝block-diag{γ0(
·
),
…
,γ0(
·
)}，满足γ0(t0)＜r0，设计如下形式的状态反馈控制器
[0167]
ui(t)＝ki(t)xi(t),i＝1,
…
,n,
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22)
[0168]
使系统
[0169]
[0170]
关于(t0,t,r,γ(
·
))有限时间稳定，其中k(t)＝block-diag{k1(t),
…
,kn(t)}。
[0171]
提出如下定理解决问题1，设计有限时间状态反馈分散控制器：
[0172]
定理2：若存在分段连续可微矩阵值函数q(
·
)∈rn×n以及连续矩阵值函数l(
·
)∈rm×n满足如下带有初始条件和终端条件的微分线性矩阵不等式组；
[0173][0174][0175][0176][0177]
那么此时系统有限时间状态反馈分散镇定控制器增益为：
[0178]ki
(t)＝l(t)q-1
(t):＝k0(t),i＝1,
…
,n.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(28)
[0179]
证明：
[0180]
不妨令且那么式(24)和式(25)可分别转化成如下形式：
[0181][0182][0183]
取p(t)＝q-1
(t)，并用p(t)同时左乘和右乘式(26)、(27)、(29)以及(30)，计算后可得
[0184][0185][0186]
p(t)＞γ0(t),t∈[t0,t0+t],
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(33)
[0187]
p(t)＜r0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(34)
[0188]
利用引理所得结论可知，系统和均关于(t0,t,r0,γ0(
·
))有限时间稳定。进一步地，再利用定理1结论可得，系统关于(t0,t,r,γ(
·
))有限时间稳定。证明完毕。
[0189]
考虑定理2中q(t)的时变性给微分线性矩阵不等式组(24)-(27)的求解带来一定的难度。从实际的角度出发，人们更倾向于将问题转移到线性矩阵不等式的框架下进行求解。下面给出一个基于线性矩阵不等式的综合方法，将矩阵值函数γ(t)取为与矩阵r同形的常值矩阵，即令γ(t)＝γ＝ρr,0＜ρ＜1且初始时间t0＝0，在此条件下，对问题1进行重新描述如下。
[0190]
问题2：给定正标量t，正定矩阵r＝block-diag{r0,
…
,r0}，设计一个如式(22)形式的状态反馈分散控制器，使得闭环系统(23)关于(t,r,ρr)有限时间镇定。
[0191]
针对此问题，给出基于线性矩阵不等式的控制器设计方法。
[0192]
定理3：若存在非负标量α1和α2，正定矩阵q∈rn×n，矩阵m0∈rm×n，满足下述线性矩阵不等式组
[0193]
[0194][0195][0196]
其中α＝max{α1,α2}。此时问题2有解，且此时分散状态反馈控制器增益为：
[0197][0198]
证明：
[0199]
由式(38)可解得将其代入式(35)和式(36)中可得：
[0200][0201][0202]
取用同时左乘与右乘式和式，可得：
[0203][0204][0205]
考虑到cond(p)＝cond(q)，易得i＝1,2。取和通过引理2结论，可知闭环系统和均关于(t,r0,ρr0)有限时间稳定。进一步由定理1结论可得，在线性矩阵不等式框架下，闭环系统(23)是关于(t,r,ρr)有限时间稳定的。证明完毕。
[0206]
综上所述，通过状态反馈能够对低维连续系统设计有限时间镇定控制器，且所得控制器通过分块对角形式可直接构建成连续对称组合系统的镇定控制器。
[0207]
下面用一个实例对本发明做进一步的说明。
[0208]
考虑图1中的机械系统，该系统由两个以弹簧相连的滑块组成，滑块在光滑平面上运动。
[0209]
分析系统特性，取状态量u＝[u1,u2]
t
＝[f1,-f2]
t
，y＝[y1,y2]
t
＝[s1,s2]
t
，建立如下系统方程：
[0210][0211]
y(t)＝cx(t).
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(44)
[0212]
其中对系统(43)(44)设计控制器，使得其状态回归平衡点x
＊
＝[a,0,b,0]
t
处。
[0213]
取误差ξ(t)＝x(t)-x
＊
，误差系统输入量误差系统输出量可得到如下误差系统：
[0214][0215][0216]
当取m1＝m2＝1kg，k＝1n/m时，注意到原系统(43)与误差系统(45)为对称组合形式。此时n＝2，c0＝[1 0]。
[0217]
对系统(45)设计状态反馈控制器，满足如下误差约束
[0218]
|ξ1(t)|/a＜δ1,
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(47)
[0219]
|ξ2(t)|＜δ2,
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(48)
[0220]
|ξ3(t)|/b＜δ1,
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(49)
[0221]
|ξ4(t)|＜δ2,
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(50)
[0222]
其中δ1、δ2分别表示x1(t)和x3(t)的相对超调量和x2(t)与x4(t)的绝对超调量。
[0223]
为满足(47)-(50)的控制需求，取c＝min{|a|,|b|},γ＝block-diag{γ0,γ0},r0＝ρ-1
γ0,0＜ρ＜1,r＝block-diag{r0,r0}，a＝4，b＝5，ρ＝0.1，δ1＝0.2，δ2＝0.9。
[0224]
根据上述仿真参数，利用matlab软件中lmi工具箱求解得到状态反馈控制增益k0＝[-2.42
ꢀ‑
11.84]，那么对称组合系统的状态反馈分散控制器的控制增益可直接由如下分块对称形式给出：
[0225][0226]
仿真结果如图2所示，基于状态反馈所设计的控制器能使闭环系统状态趋向给定的期望值x
＊
＝[4,0,5,0]
t
处，且各状态均未超出事先设定的超调需求，可知本发明所得的状态反馈分散控制其能够使闭环系统有限时间稳定，证明本发明的有效性。
[0227]
上述结果表明本发明的控制方法解决对称组合系统有限时间稳定控制器设计问题，并利用大系统的结构特性简化计算复杂度。