一种基于实测数据的可疑点判别方法与流程

本发明涉及基于实测数据的可疑点判别方法。

背景技术：

公路现场的实测数据的合格标准我们称作规范，规范是国标，更新的情况较为普遍，因此，我们需要做到整个系统的及时更新，且不同的地理特征条件下的实测数据的标准也许会有不同，针对不同地区，可能会存在日后需要考察的问题出现；且核心技术较简单，主要是几个程序的组合，但是数据库较大，会影响运行速度。公路现场实测上报数据不真实的现象很普遍，但是大面积不合格的数据施工单位并不会谎报数据，一定会进行复测并进行重新的摊铺、碾压，但是个别数据的人为修改，这种情况很普遍且不易察觉，然而个别数据的不合格显示的正是小区间范围内的路段的质量不合格，容易造成应力集中或是提前使道路进入疲劳期，影响整条公路的正常运行，且后期维修、养护费用就会大幅度地提高，造成人力、财力的双重浪费。以及对不同城市的空气污染状况进行分析，实测上报数据不真实的现象很普遍，对个别数据的人为修改，这种情况很普遍且不易察觉，造成后期处理人力、财力的双重浪费，故需要查找可疑数据，然而现有技术查找可疑数据的精确度低、速度慢，需要一种快速、高精度的方法查找可疑数据。

技术实现要素：

本发明的目的是为了解决现有现场实测上报数据不真实，查找可疑数据的精确度低、速度慢的缺点，而提出一种基于实测数据的可疑点判别方法。

一种基于实测数据的可疑点判别方法具体过程为：

步骤一、计算n个实测数据所在位置中的任意两个实测数据所在位置之间的距离，得到n个实测数据所在位置间的距离矩阵，n的取值范围为正整数；

步骤二、初始第一步i＝1时，n个实测数据各自构成一类，类的个数k＝n，此时类间距离就是n个实测数据所在位置中任意两个实测数据所在位置之间的距离，k为正整数，i为正整数；

步骤三、i＝2时，对步骤二得到的类间距离最小的两类进行合并，成为一个新类，此时类的个数k＝n-1；计算新类与其他类之间的距离，得到新的类间距离矩阵；

步骤四、i＝m时，对i＝m-1时得到的类间距离最小的两类进行合并，成为一个新类，此时类的个数k＝n-i+1，m为正整数；

步骤五、如果步骤四合并后类的个数k仍大于1，重复步骤四和步骤五，直到类的个数为1时，得到谱系聚类图，即可得到类的个数及各类的成员；

步骤六、根据类的个数及各类的成员选取步长最长或选取最后合并的实测数据，作为可疑点数据，并判定可疑点数据的可疑程度。

本发明的有益效果为：

本发明提出的一种基于实测的上报数据可疑点分析方法，能够快速、准确的找出造假数据的可疑点，并具体指出具体的可疑点位置，让现场的工作人员进行复测，确保实测上报数据的真实，避免造成应力集中或是提前使道路进入疲劳期，影响整条公路的正常运行的情况，大大降低了后期维修、养护费用，降低经济损失、节省人工。

在已经确定路面的压实度指标时，用本发明提出的一种基于实测的上报数据可疑点分析方法进行拟合，查找可疑点，并对结果进行分析，结果的精确度已经达到98％以上，且对于路面结构的其他连续性指标均有较好的拟合效果，由此可以判断，本发明方法在技术上可行，是可以在施工单位推广的，而且会有很好的效果，为施工单位提供方便。

例如在京津冀地区的13个城市的相对地理信息见图2-图8；根据6幅图片，对京津冀13座城市的AQI的数据进行分析,发现唐山的AQI数值难与其他城市聚类，根据面板匹配法及地理信息因素，唐山的空气污染状况应与天津、秦皇岛、承德相近，而天津、秦皇岛、承德的AQI数值却是相近，因此认为唐山的AQI数据存在造假的可能性，而作为唐山市主要污染物的PM2.5的数据并没有发现有可疑的现象，进行所有污染物的对比分析，我们认为唐山市的SO₂数据造假；

同理，我们对长三角地区进行分析，宁波SO₂、PM2.5数据造假；

同理，我们对珠三角地区进行分析，经分析，珠三角地区肇庆PM2.5、PM10数据造假，肇庆SO₂数据造假，广州SO₂数据造假。

由此可以判断，本发明方法在技术上可行，是可以推广的，而且会有很好的效果，为检测单位提供方便。

附图说明

图1为本发明流程图；

图2为京津翼地区PM₁₀平均联接(组间)的树状图，横坐标为步长；

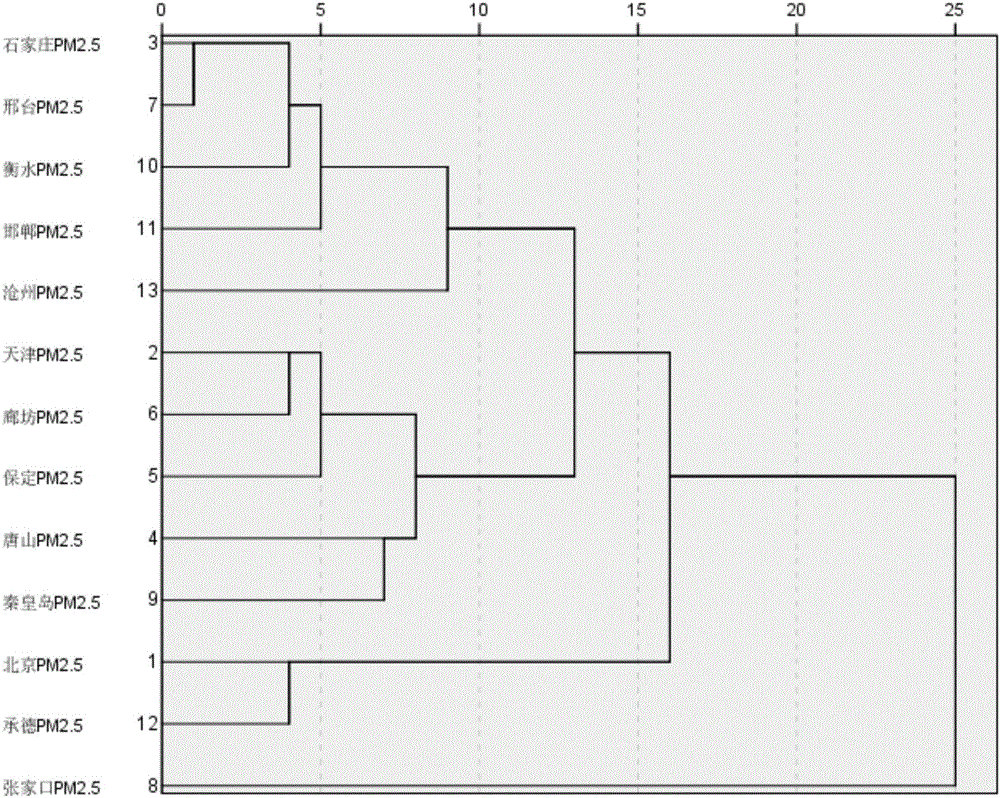
图3为京津翼地区PM_2.5平均联接(组间)的树状图，横坐标为步长；

图4为京津翼地区SO₂平均联接(组间)的树状图，横坐标为步长；

图5为京津翼地区CO平均联接(组间)的树状图，横坐标为步长；

图6为京津翼地区NO₂平均联接(组间)的树状图，横坐标为步长；

图7为京津翼地区AQI平均联接(组间)的树状图，横坐标为步长；

图8为小波图像分解过程(重构时逆向即可)图；

图9为小波基函数的相平面图；

图10为嵌套的多分辨率子空间图，V0为原信号的频率空间，V1为经第一级分解后V0被分解成的低频子空间；V2为经第二级分解后V0被分解成的低频子空间；V3为经第三级分解后V0被分解成的低频子空间；W1为经第一级分解后V0被分解成的高频子空间；W2为经第二级分解后V0被分解成的高频子空间；W3为经第三级分解后V0被分解成的高频子空间；W4为经第四级分解后V0被分解成的高频子空间。

具体实施方式

具体实施方式一：结合图1说明本实施方式，本实施方式的一种基于实测数据的可疑点判别方法具体是按照以下步骤进行的：

聚类分析方法

聚类分析法，又称群分析，是根据失误本身的特性，研究对样品或指标进行分类的一种多元的统计方法。所谓的“类”，通俗地说就是相似元素的集合。聚类分析的原则是直接比较各事物之间的性质，将性质相似的归为一类，将性质差别较大的归入不同的类。

聚类分析法是实用多元统计分析的一个新的分支，正处于发展阶段，理论上虽然并不是很完善，但是它却能解决很多的实际问题，因此这个方法很受人们的重视。其功能是选择一中度量个体接近程度的统计量，建立一种分类方法，并按接近程度对观测对象给出合理的分类。

聚类分析的内容十分丰富，按其聚类的方法可分为以下几种：系统聚类法、动态聚类法、最优分割法、模糊聚类法、图论聚类法等。系统聚类法是目前在实际应用中使用最广泛的一种分类方法，本发明即使用的是系统聚类法。

设有X个样品，每个样品测得某项指标抽样调查的若干实测数据点。系统聚类分析法的基本思想是：首先定义样品的距离(或相似系数)，这是类间的距离(或相似系数)，这时类间的距离与样品间的距离是等价的；然后将距离最近的两类合并成新类，并计算新类与其他类的类间距离，再按最小距离准则并类，这样每次缩小一类，直到所有的样品都并成一类为止，这个并类过程可以用谱系聚类形象地表达出来。

由以上系统聚类法的基本思想，可以得到它的基本步骤如下：聚类分析方法是在SPSS软件中实现的；

步骤一、计算n个实测数据所在位置中的任意两个实测数据所在位置之间的距离，得到n个实测数据所在位置间的距离矩阵，n的取值范围为正整数；

步骤二、初始第一步i＝1时，n个实测数据各自构成一类，类的个数k＝n，此时类间距离就是n个实测数据所在位置中任意两个实测数据所在位置之间的距离，k为正整数，i为正整数；

步骤三、i＝2时，对步骤二得到的类间距离最小的两类进行合并，成为一个新类，此时类的个数k＝n-1；计算新类与其他类之间的距离，得到新的类间距离矩阵；

步骤四、i＝m时，对i＝m-1时得到的类间距离最小的两类进行合并，成为一个新类，此时类的个数k＝n-i+1，m为正整数；

步骤五、如果步骤四合并后类的个数k仍大于1，重复步骤四和步骤五，直到类的个数为1时，得到谱系聚类图，即可得到类的个数及各类的成员；

步骤六、根据类的个数及各类的成员选取步长最长或选取最后合并的实测数据(比如如图7中的13或图6中的8)，作为可疑点数据，并判定可疑点数据的可疑程度。

小波即小区域的波，是一种特殊的长度有限、平均值为零的波形。它有两个特点：一是“小”，即在时域具有紧支集或近似紧支集；二是正负交替的“波动性”，也即支流分量为零。

连续小波基函数

所谓小波(Wavelet)，即存在于一个较小区域的波。小波函数的数学定义是：设ψ(t)为一平方可积函数，即ψ(t)∈L²(R)，若其傅立叶变换满足：

$C_{\mathrm{\&psi;}}={\&Integral;}_R\frac{{\left|\stackrel{\&OverBar;}{\mathrm{\&psi;}}\left(\stackrel{\&OverBar;}{w}\right)\right|}^2}{\left|w\right|}\mathrm{dw}<\&infin;$

时，则称ψ(t)为一个基本小波或小波母函数，并称上式是小波函数的可容许条件。

根据小波函数的定义，小波函数一般在时域具有紧支集或近似紧支集，即函数的非零值定义域具有有限的范围，这即所谓“小”的特点；另一方面，根据可容许性条件可知ψ(w)|_w＝0＝0，即直流分量为零，因此小波又具有正负交替的波动性。

将小波母函数ψ(t)进行伸缩和平移，设其伸缩因子(亦称尺度因子)为a，平移因子为b，并记平移伸缩后的函数为ψ_a,b(t)，则：

${\mathrm{\&psi;}}_{a,b}\left(t\right)=|a{|}^{-\frac{1}{2}}\mathrm{\&psi;}\left(\frac{t-\mathrm{\&tau;}}{a}\right),a,b\&Element;R;a\&NotEqual;0$

并称τ为参数,ψ_a,b(t)小波基函数。由于a和b均取连续变换的值，因此又称为连续小波基函数，它们是由同一母函数经伸缩和平移后得到的一组函数系列。

定义小波母函数ψ(t)的窗口宽度为Δt，窗口中心为t₀，则可以求得连续小波基函数ψ_a,b(t)的窗口中心及窗口宽度分别为：

t_a,b＝at₀+b,Δt_a,τ＝aΔt

设是ψ(t)的傅立叶变换，频域窗口中心为w₀，窗口宽度为Δw，ψ(t)的傅立叶变换为则有:

${\stackrel{\&OverBar;}{\mathrm{\&psi;}}}_{a,b}\left(\stackrel{\&OverBar;}{w}\right)=\sqrt{\left|a\right|}{e}^{-jwb}\mathrm{\&phi;}\left(aw\right)$

所以此时频域窗口中心及窗口宽度分别为：

$w_{a,b}=\frac{1}{a}{w}_0,{\mathrm{\&Delta;w}}_{a,b}=\frac{1}{a}\mathrm{\&Delta;}w$

由此可见，连续小波的时、频窗口中心和宽度均是尺度因子a的函数，均随着a的变化而伸缩，并且还有

Δt_a,b·Δw_a,b＝Δt·Δw

即连续小波基函数的窗口面积是不变的，这正是Heisenberg测不准原理。将不同a、b值下的时频窗口绘在同一个图上，就得到小波基函数的相平面(如图9所示)。

对不同的频率成分，在时域上的取样步长是可调的，高频者(对应小的m值)采样步长小，低频者(对应大的m值)采样步长大。也就是说，小波变换能实现了窗口的大小固定，形状可变的时频局部化，见图9。正是这个意义上小波变换被誉为数学“显微镜”。连续小波变换

将L²(R)空间的任意函数f(t)在小波基下进行展开，称其为函数f(t)的连续小波变换CWT，变换式为：

${\mathrm{WT}}_f(a,b)=<f,{\mathrm{\&psi;}}_{a,b}>=\frac{1}{\sqrt{\left|a\right|}}{\&Integral;}_{R}f\&CenterDot;\stackrel{\&OverBar;}{\mathrm{\&psi;}\left(\frac{t-b}{a}\right)}dt$

当小波的容许性条件成立时，其逆变换为：

$f\left(t\right)=\frac{1}{C_{\mathrm{\&psi;}}}{\&Integral;}_{-\mathrm{\&infin;}}^{+\mathrm{\&infin;}}\frac{da}{a^2}{\&Integral;}_{-\mathrm{\&infin;}}^{+\mathrm{\&infin;}}{\mathrm{WT}}_f(a,b)\&CenterDot;\mathrm{\&psi;}\left(\frac{t-b}{a}\right)db$

其中为ψ(t)的容许性条件

我们可以这样理解，傅立叶分析是将信号分解成一系列不同频率的正弦波的叠加，同样小波分析是将信号分解为一系列小波函数的叠加，而这些小波函数都是由一个母小波函数经过平移和尺度伸缩得来的。小波分析优于傅立叶分析的地方是，它在时域和频域同时具有良好的局部化性质。而且由于对高频成分采用逐渐精细的时域或频域取样步长，从而可以聚焦到对象的任何细节，所以被称为“数学显微镜”。小波分析广泛应用与信号处理、图像处理、语音识别等领域。

可以这样理解小波变换的含义：打个比喻，我们用镜头观察目标信号f(t)，ψ(t)代表镜头所起的所用。b相当于使镜头相对于目标平行移动，a的所用相当于镜头向目标推进或远离。由此可见，小波变换有以下特点：

多尺度/多分辨的特点，可以由粗及细地处理信号；

可以看成用基本频率特性为ψ(ω)的带通滤波器在不同尺度a下对信号做滤波。

适当地选择小波，使ψ(t)在时域上为有限支撑,(ω)在频域上也比较集中，就可以使WT在时、频域都具有表征信号局部特征的能力。

离散小波变换

计算机中的图像信息是以离散信号形式存放的，所以需要将连续小波变换离散化。而最基本的离散化方法就是二进制离散，一般将这种经过离散化的小波及其变换叫做二进小波和二进变换。需要注意的是这里的离散化都是针对连续的尺度因a和连续平移因子b的，而不是针对时间t的。这儿限制尺度因子a总是正数。

(1)尺度与位移的离散化

对连续小波基函数ψ_a,b(t)尺度因子a和平移因子b进行离散化可以得到离散小波变换WT_f(a,b)，从而减少小波变换系数的冗余度。在离散化时通常对尺度因子a和平移因子b按幂级数进行离散化，即取(m为整数，a₀≠1,但一般都假定a₀＞1)，得到离散小波函数为：

${\mathrm{\&psi;}}_{m,n}\left(t\right)=\frac{1}{\sqrt{\left|a_0\right|}}\mathrm{\&psi;}\left(\frac{t-{\mathrm{na}}_0^m{b}_0}{a_0^m}\right)=\frac{1}{\sqrt{\left|a_0\right|}}\mathrm{\&psi;}(a_0^{-m}t-{\mathrm{nb}}_0)$

其对应系数为：

$C_{m,n}=<f\left(t\right),{\mathrm{\&psi;}}_{m,n}>={\&Integral;}_{-\mathrm{\&infin;}}^{+\mathrm{\&infin;}}f\left(t\right)\stackrel{\&OverBar;}{{\mathrm{\&psi;}}_{m,n}\left(t\right)}dt$

(2)二进制小波变换

二进小波变换是一种特殊的离散小波变换，特别地令参数a₀＝2，b₀＝1，则有 该二进尺度分解的原理在二十世纪三十年代由Littlewood和Paley在数学上进行了研究证明。

离散小波变换为：

${\mathrm{WT}}_f(m,n)=<m,n>={\&Integral;}_{-\mathrm{\&infin;}}^{+\mathrm{\&infin;}}f\left(t\right){\mathrm{\&psi;}}_{m,n}\left(t\right)dt$

离散二进小波变换为：

多分辨率分析

Mallat在构造正交小波基时提出了多分辨率分析(Multi-Resolution Analysis)的概念，从空间概念上形象地说明了小波的多分辨率特性，并将在此之前的所有正交小波基的构造法统一起来，给出了正交小波的构造方法以及正交小波的快速算法——Mallat算法。Mallat算法在小波分析中的地位相当于快速傅立叶变换在经典傅立叶分析中的地位。

多分辨率分析可形象地表示为一组嵌套的多分辨率子空间(如图10所示)。

假设原信号的频率空间为V₀，经第一级分解后V₀被分解成两个子空间：低频的V₁和高频的W₁；经第二级分解后V₁被分解成低频的V₂和高频的W₂。这种子空间的分解过程可以记为：

$V_0=V_1\&CirclePlus;W_1,V_1=V_2\&CirclePlus;W_2,V_2=V_3\&CirclePlus;W_3,\mathrm{...},V_{N-1}=V_N\&CirclePlus;W_N$

其中符号表示两个子空间的“正交和”；V_f代表与分辨率2^-j对应的多分辨率分析子空间；与尺度函数相对应的小波函数的伸缩和平移构成的矢量空间W_j是V_j的正交补空间；各W_j是反映V_j-1空间信号细节的高频子空间，V_j是V_j-1反映空间信号概貌的低频子空间。由离散小波框架可得到子空间的以下特性：

$V_0=V_1\&CirclePlus;W_1=V_2\&CirclePlus;W_2\&CirclePlus;W_1=V_N\&CirclePlus;W_N\&CirclePlus;W_{N-1}\&CirclePlus;\mathrm{...}{W}_2\&CirclePlus;W_1$

这一结果表明：分辨率为2⁰＝1的多分辨率分析子空间V₀可以用有限个子空间来逼近。利用小波对信号进行处理的一般步骤

小波的应用主要是信号的处理，其中最典型的应用是小波图象压缩。另外，小波在诸如信号去噪、特征提取等多方面均有成功的应用。下面以图象去噪为例说明小波应用策略。小波的各种应用均可分为以下三步：

1)对输入到Matlab软件的小波分析工具箱中的可疑点数据作小波变换，将可疑点数据由空域变换到频域；

2)对小波系数做相应处理；

3)对处理后的小波系数做小波逆变换，重构还原原可疑点数据；小波图像去噪

因为噪声信号多包含在具有较高频率的细节中，所以小波去噪首先对图像信号进行小波分解，可利用门限阈值对所分解的小波系数进行处理，然后对图像信号进行小波重构，抑制图像信号中的无用部分，恢复图像信号中的有用部分。如图8所示，具体步骤为：

1)可疑点数据的小波分解：选择合适的小波及恰当的分解层次N，对可疑点数据进行N层的小波分解；

2)对分解后的高频系数进行阈值量化：对于分解的每一层，选择恰当的阈值，对该层高频系数进行阈值量化处理；

利用软阈值或硬阈值门限处理相应的小波系数,获得新的被压缩的小波系数；

3)重构可疑点数据：根据小波分解后的第N层近似的低频系数和经过阈值量化处理后的细节高频系数，重构可疑点数据；如图8；

c(x,y)为随x、y变化的系数，x为在时域上的取样步长，y为在频域上的取样步长，x、y为整数；cA₁、cH₁、cV₁、cD₁为对目标图像进行的第一层小波分解后得到的新的目标图像；cA₂、cH₂、cV₂、cD₂为对目标图像进行的第二层小波分解后得到的新的目标图像；

其二层小波可疑点数据重构过程正好与此相反，基于小波变换的图像处理，是通过对图像分解过程中所产生的近似分量与细节分量系数的调整，使重构图像满足特定条件，而实现图像处理。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤一中计算n个实测数据所在位置中的任意两个实测数据所在位置之间的距离，得到n个实测数据所在位置间的距离矩阵，n的取值范围为正整数；具体过称为：

通过皮尔逊相关系数距离得到n个实测数据所在位置中任意两个实测数据所在位置之间的距离。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一或二不同的是：所述步骤三中i＝2时，对步骤二得到的类间距离最小的两类进行合并，成为一个新类，此时类的个数k＝n-1；计算新类与其他类之间的距离，得到新的类间距离矩阵；具体过称为：

通过SPSS(统计产品与服务解决方案)软件的默认方法类间平均链锁法，计算新类 与其他类之间的距离，得到新的类间距离矩阵。

用SPSS软件的系统聚类法(Hierarchical Cluster)，对不同样品的一种数据值数据进行聚类分析。具体的聚类方法是类间平均锁链法(Between-groups linkage)，在选择距离测量上，选用皮尔逊相关系数(Pearson correlation)。聚类区域就是整段路的每隔3米的一个区段。

具体实施方式四：本实施方式与具体实施方式三不同的是：所述SPSS软件为统计产品与服务解决方案软件。

具体实施方式五：本实施方式与具体实施方式一、二或四不同的是：所述步骤五中类的个数为合并的次数，各类的成员为该类合并时包含的实测数据。

具体实施方式六：本实施方式与具体实施方式3不同的是：所述步骤五中类的个数为合并的次数，各类的成员为该类合并时包含的实测数据。

具体实施方式七：本实施方式与具体实施方式一、二、四或六不同的是：所述步骤六中根据类的个数及各类的成员选取步长最长或选取最后合并的实测数据，作为可疑点，并判定可疑点的可疑程度；具体过称为：

将可疑点输入到Matlab软件的小波分析工具箱，得到不同区域随时间变化的实测数据的变化趋势，依据得到的聚类分析树状图的步长判定可疑点的可疑程度，判定可疑点的可疑程度。

具体实施方式八：本实施方式与具体实施方式五不同的是：所述步骤六中根据类的个数及各类的成员选取步长最长或选取最后合并的实测数据，作为可疑点，并判定可疑点的可疑程度；具体过称为：

将可疑点输入到Matlab软件的小波分析工具箱，得到不同区域随时间变化的实测数据的变化趋势，依据得到的聚类分析树状图的步长判定可疑点的可疑程度，判定可疑点的可疑程度。

具体实施方式九：本实施方式与具体实施方式三不同的是：所述步骤六中根据类的个数及各类的成员选取步长最长或选取最后合并的实测数据，作为可疑点，并判定可疑点的可疑程度；具体过称为：

将可疑点输入到Matlab软件的小波分析工具箱，得到不同区域随时间变化的实测数据的变化趋势，依据得到的聚类分析树状图的步长判定可疑点的可疑程度，判定可疑点的可疑程度。

采用以下实施例验证本发明的有益效果：

实施例一：

本实施例一种基于实测数据的可疑点判别方法具体是按照以下步骤制备的：

已经确定路面的压实度指标可以用本系统中的程序进行拟合，查找可疑点，并对结果进行分析，结果的精确度已经达到98％以上，且对于路面结构的其他连续性指标均有较好的拟合效果，由此可以判断，我们的系统在技术上可行，是可以在施工单位推广的，而且会有很好的效果，为施工单位提供方便。

实施例二：

以京津冀地区为例分析，数据的造假情况；

京津冀地区的13个城市的相对地理信息见图2-7；

根据上面6幅图片，基于面板匹配法的基本原则，对京津冀13座城市的PM2.5的数据进行分析，经分析，京津冀地区以PM2.5作为首要污染物的城市有：保定、保定、沧州、邯郸、衡水、廊坊、石家庄、唐山、天津、邢台十座城市，经研究表明，这八座城市的地理位置与污染物数据匹配较好，不存在数据造假的可能性；对京津冀13座城市的PM10数据进行分析，京津冀地区以PM10作为首要污染物的城市有：承德、秦皇岛、张家口三座城市，我们比对AQI的聚类分析表，认为三座城市的地理位置均与秦皇岛临近，且秦皇岛与承德的AQI值相近，可以认为这两座城市的数据真实，则张家口的PM10数据造假；对京津冀13座城市的AQI的数据进行分析,发现唐山的AQI数值难与其他城市聚类，根据面板匹配法及地理信息因素，唐山的空气污染状况应与天津、秦皇岛、承德相近，而天津、秦皇岛、承德的AQI数值却是相近，因此认为唐山的AQI数据存在造假的可能性，而作为唐山市主要污染物的PM2.5的数据并没有发现有可疑的现象，进行所有污染物的对比分析，我们认为唐山市的SO₂数据造假；

同理，我们对长三角地区进行分析，宁波SO₂、PM2.5数据造假；

同理，我们对珠三角地区进行分析，经分析，珠三角地区肇庆PM2.5、PM10数据造假，肇庆SO₂数据造假，广州SO₂数据造假。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。