一种快速确定能量最优拦截预测命中点的数值优化方法与流程

本发明涉及航天器拦截交会控制领域，具体涉及一种快速确定能量最优拦截预测命中点的数值优化方法。
背景技术：
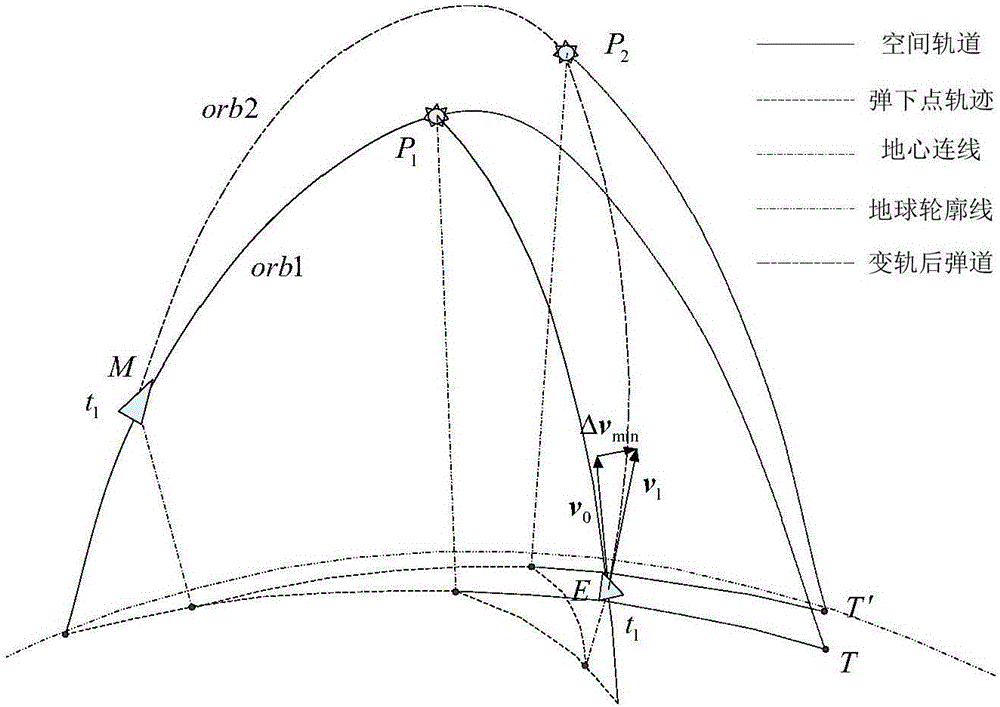
：在一般的轨道拦截问题中，需要解决的一个基本问题是在预定时间内，如何从空间中的一点到达另外一点，这类航天动力学中的两点边值问题被称为Lambert问题。数学家Gauss给出了Lambert问题的经典求解，如图1所示，Gauss问题的定义为：给定初始位置矢量r1、终端位置矢量r2，以及从r1到r2的飞行时间tF和运动方向，求初始和终端的速度矢量ν1和ν2。在Kepler轨道运动的前提条件下，位置矢量r1、r2，和速度矢量ν1、ν2共面，所以有r2=fr1+gv1v2=f·r1+g·v1---(1)]]>其中g=r1r2sinΔνμP=t-a3μ(ΔE-sinΔE)---(3)]]>f·=μPtanΔν2(1-cosΔνP-1r1-1r2)=-μar1r2sinΔE---(4)]]>g·=1-r1P(1-cosΔν)=1-ar2(1-cosΔE)---(5)]]>对于拦截问题，一般知道初始点需要多大的速度，可以使飞行器沿着一条Kepler轨道，滑行至终点。由公式(1)，可以将初始速度表示为v1=r2-fr1g---(6)]]>所以，Gauss问题的求解可以简化为系数f、g，以及和的求解。受超越方程的限制，必须用逐次逼近法求解，可将Gauss问题的一般解法概括如下：1、给定P、a或ΔE中任意一个未知数的初值；2、由公式(2)和(4)计算另两个未知数的值；3、由公式(3)求解时间t，并与给定的飞行时间tF比较，检验计算结果；4、若计算结果t与给定时间tF不一致，修正迭代变量，并重复步骤2与步骤3。对于目标改变了运动轨道时，确定能量最优预测命中点的数值优化方法问题，也就是拦截变轨最小速度修正问题，如图2所示，t1表示动能拦截武器E主动段关机点的时刻，M表示机动弹头，T表示打击目标在地面的位置。P1表示如果机动弹头在t1时刻不进行变轨，则拦截弹会与弹头在该点相撞，即P1表示原预测命中点。如果弹头在t1时刻按一定的突防策略进行轨道机动，假设目标M从实线表示的轨道orb1改变到点划线表示的轨道orb2，打击目标也随之修改至T′，则当前时刻t1的拦截器E无法以当前速度v0，在新的目标轨道orb2上拦截目标M。假设新的命中点位置是P2，则飞行器的初始速度必须修正为v1，v1可以通过求解Gauss问题获得。不同于以往的拦截交会问题，当目标存在轨道机动时，拦截器选择不同的预测命中点P2将带来不同的速度修正Δv＝v1-v0。显然，对于燃料有限的拦截器而言，速度修正量Δv＝|Δv|最小的机动策略才是最优的，此时的预测命中点P2与飞行时间tF也分别是最优拦截位置与拦截时间。对于上述确定能量最优预测命中点的数值优化方法问题，传统的求解方法是对时间t进行迭代搜索。P迭代法是假定一个P的试探值，并由此值计算出另外两个未知数a和ΔE，然后解出t，并把它与给定的飞行时间tF比较，以此检验试探值是否合适。P迭代法可以得出t随P变化曲线斜率的解析表达式，因此可用牛顿迭代法修正P的试探值，提高迭代速度。定义三个常量由Kepler轨道理论，a可以表示为a=mkp(2m-l2)P2+2klP-k2---(8)]]>进一步地，由公式(2)、(3)、(4)，可以求出时间tt=g+a3μ{arccos[1-r1a(1-f)]+r1r2f·μa}---(9)]]>另外，t随P变化曲线斜率的解析表达式为dtdP=-g2P-32a(t-g)(k2+(2m-l2)P2mkP2)+a3μ2ksinΔEP(k-lP)---(10)]]>所以，利用P迭代法求解Gauss问题的步骤可以表述为1、由公式(7)，计算常数k，l和m；2、给定自变量P的试探值；3、由公式(8)，计算a的值；4、由公式(2)、(3)、(4)，计算f、g和的值；5、由公式(9)，计算时间t，并与给定的飞行时间tF比较；如果相等，则结束；不相等，转步骤6；6、结合公式(10)，并使用牛顿迭代法计算自变量P的新试探值，并转步骤3。本发明所要探讨的确定能量最优预测命中点的数值优化方法问题，其运动模型可以简化为图3中O代表地心；r1是拦截弹的初始位置矢量，r2是拦截弹与目标的碰撞点，即拦截弹的终端位置矢量；v0是拦截弹机动前的速度矢量，用虚线表示；v1是通过求解Gauss问题所求得的初始速度，用实线表示；r2与v1的上标代表不同的碰撞点以及与之对应的拦截弹初始速度。在已知目标轨道信息的条件下，目标轨道的升交点赤经Ω、轨道倾角i、近地点幅角ω、半长轴aM和偏心率eM，以及通过近地点时刻tpM可以整理为轨道根数的形式[Ω,i,aM,eM,ω,tpM]终端位置矢量r2受给定飞行时间tF限制。以下，在不引起误会的条件下，将给定飞行时间简称为拦截时间t。其中，目标运动的偏近点角EM和真近点角fM随拦截时间t的迭代函数为EM=2·arctan[1-eM1+eMtan(fM2)]EM-eMsin(EM)=2πTM(t-tpM)---(11)]]>其中，目标的轨道周期为TM。所以，终端位置矢量r2可以表示为r2=aM(1-eM2)1+eMcos(fM)]]>r2=cos(fM+w)cosΩ-sin(fM+w)cosisinΩcos(fM+w)sinΩ+sin(fM+w)cosicosΩsin(fM+w)sini·r2---(12)]]>至此，已经可以通过传统方法求解目标存在轨道机动的拦截变轨最小速度修正问题。传统方法需要设计两重迭代：内层迭代可以通过P迭代法求解Gauss问题，获得某一预测命中点P2所对应的速度修正量Δv；外层迭代则是通过计算不同P2对应的Δv，从而确定最小速度修正量Δvmin。计算流程图如图4所示，其中外层迭代使用半分法加速收敛。虽然这类搜索算法思路简单，计算精度也能满足工程实际，但是耗时较长，即使使用半分法加速搜索，也不利于在线求解。技术实现要素：为了解决上述技术问题，本发明提供一种快速确定能量最优拦截预测命中点的数值优化方法，其基于最优规划理论，通过对拦截变轨最小速度修正问题进行数学建模，经过大量的公式推导，获得了Δvmin对应的KKT条件，并通过设计牛顿迭代算法，获得了解析的梯度信息，实现了对Δvmin的快速求解，同时也求解出最优拦截位置与拦截时间。该方法计算精度高，速度快，且对初值不敏感。本发明采用以下的技术方案：一种快速确定能量最优拦截预测命中点的数值优化方法，具体步骤如下：(1)、给定自变量X的试探值，并设定系数矩阵u和v；(2)、由公式(22)和公式(24)计算偏导数矩阵FF′(X)；(3)、由公式(25)计算新的自变量取值Xk+1；(4)、判断是否收敛；如果ΔXX＝XXk+1-XXk小于误差限，计算结束；否则转至步骤(2)，重复进行步骤(2)-(4)；其中，步骤(1)中，所述自变量X＝[tPfM]T，引入两组等式约束f1=g+a3μ{arccos[1-r1a(1-f)]+r1r2f·μa}-t]]>f2=EM(fM)-eMsin[EM(fM)]-2πTM(t-tpM)]]>使拦截弹的速度修正量最小，描述为数学表达式，则目标函数为J(X)＝(v1x-v0x)2+(v1y-v0y)2+(v1z-v0z)2；至此，把目标存在轨道机动的拦截变轨最小速度修正问题，转化为一个含有等式约束的最优规划问题，该最优规划问题的表达式整理如下：X＝[tPfM]TJ(X)＝(v1x-v0x)2+(v1y-v0y)2+(v1z-v0z)2f1(t,P,fM)=g+a3μ{arccos[1-r1a(1-f)]+r1r2f·μa}-t---(13)]]>f2(t,fM)=EM(fM)-eMsin[EM(fM)]-2πTM(t-tpM)]]>设带有Lagrange乘子的增广目标函数为L＝J+λ1f1+λ2f2(14)由KKT条件，可得∂L∂t=-λ1-2πTMλ2=0---(15)]]>∂L∂P=∂J∂P+λ1∂f1∂P=0---(16)]]>∂L∂fM=∂J∂fM+λ1∂f1∂fM+λ2∂f2∂fM=0---(17)]]>由公式(15)与(16)，解得λ1=-∂J/∂P∂f1/∂Pλ2=-TM2πλ1=TM2π∂J/∂P∂f1/∂P---(18)]]>将公式(18)代入公式(17)，得到等式f3(P,fM)=∂J∂fM-∂J/∂P∂f1/∂P∂f1∂fM+TM2π∂J/∂P∂f1/∂P∂f2∂fM---(19)]]>所以，KKT条件最终转化为三个等式约束f1(t,P,fM)=0f2(t,fM)=0f3(P,fM)=0---(20)]]>设F(X)＝[f1f2f3]T(21)则方程组(21)的解就是拦截变轨最小速度修正问题的最优解；步骤(2)中，所述公式(22)为方程组F(X)的Jacobi矩阵具体为：F′(X)=∂f1∂t∂f1∂P∂f1∂fM∂f2∂t0∂f2∂fM0∂f3∂P∂f3∂fM---(22)]]>其中，因为f2中不显含P，f3中不显含t，所以则自变量X的迭代公式可以写为：XK+1＝XK-[F′(XK)]-1·F(XK)(23)为提高数值计算的稳定性，公式(22)可以转化为公式(24)，所述公式(24)为：其中，对角阵u和v为步骤(1)所述的系数矩阵；所述公式(25)为：如上所述的方法，优选地，所述公式(22)中，各项的解析表达式如下：因为并且，显然∂f1∂t=-1∂f2∂t=-2πTM---(27)]]>所以，只需获得所述J、f1、f2对P、fM的一阶偏导，二阶纯偏导，以及二阶混合偏导，即可获得公式(22)的解析表达式；将矢量投影在大地直角坐标系，并约定h2xh2yh2z=cos(fM+w)cosΩ-sin(fM+w)cosisinΩcos(fM+w)sinΩ+sin(fM+w)cosicosΩsin(fM+w)sini---(28)]]>则首先，给出J对P、fM的一阶偏导，二阶纯偏导，以及二阶混合偏导，设JPy1=r2y(fM)g(P,fM)-r1yf(P,fM)g(P,fM)-v0y;JPy2=r2y(fM)-r1y[2-f(P,fM)]2·P·g(P,fM);]]>JPz1=r2z(fM)g(P,fM)-r1zf(P,fM)g(P,fM)-v0z;JPz2=r2z(fM)-r1z[2-f(P,fM)]2·P·g(P,fM);]]>r1h2＝r1xh2x+r1yh2y+r1zh2z；则因为∂h2x∂fM∂h2y∂fM∂h2z∂fM=-sin(fM+w)cosΩ-cos(fM+w)cosisinΩ-sin(fM+w)sinΩ+cos(fM+w)cosicosΩcos(fM+w)sini]]>∂g∂fM=1μP·[∂r2∂fM·sr12h2-r2·r1ph2·r1h2sr12h2]]]>∂∂fMf(P,fM)g(P,fM)=∂f∂fM·g-f·∂g∂fMg2]]>所以，设∂∂fMr2x(fM)g(P,fM)=(∂r2∂fM·h2x+r2·∂h2x∂fM)g-r2·h2x·∂g(P,fM)∂fMg2(P,fM);JfM×2=∂∂fMr2x(fM)g(P,fM)-r1x·∂∂fMf(P,fM)g(P,fM)]]>∂∂fMr2y(fM)g(P,fM)=(∂r2∂fM·h2y+r2·∂h2y∂fM)g-r2·h2y·∂g(P,fM)∂fMg2(P,fM);JfMy2=∂∂fMr2y(fM)g(P,fM)-r1y·f(P,fM)g(P,fM)]]>∂∂fMr2z(fM)g(P,fM)=(∂r2∂fM·h2z+r2·∂h2z∂fM)g-r2·h2z·∂g(P,fM)∂fMg2(P,fM);JfMz2=∂∂fMr2z(fM)g(P,fM)-r1z·∂∂fMf(P,fM)g(P,fM)]]>则∂2J∂P2=-12P∂J∂P+2·(JPx22+JPy22+JPz22)+1Pg∂f∂P·(JPx1·r1x+JPy1·r1y+JPz1·r1z)---(32)]]>因为所以因为∂2r2∂fM2=2e2-e2cos2(fM)+ecos(fM)[1+ecos(fM)]2r2]]>∂2h2x∂fM2∂2h2y∂fM2∂2h2z∂fM2T=-h2xh2yh2zT]]>∂2g∂fM2=1μP[∂2r2∂fM2sr12h2-2·∂r2∂fMr1ph2·r1h2sr12h2-r2·(r1ph22-r1h22)·r12+r1h24sr12h23]]]>∂2f∂fM2=1r1P[2·∂r2∂fM·r1ph2-r2·r1h2-∂2r2∂fM2·(r1-r1h2)]]]>∂2f(P,fM)∂fM2g(P,fM)=∂2f∂fM2g-f∂2g∂fM2-2∂f∂fM∂g∂fM+2fg(∂g∂fM)2g2]]>所以，设∂2∂fM2r2·h2xg(P,fM)=(∂2r2∂fM2·h2x+2∂r2∂fM∂h2x∂fM-r2h2x)·g-r2·h2x·∂2g∂fM2-∂∂fMr2·h2xg(P,fM)·2g·∂g∂fMg2(P,fM)]]>∂2∂fM2r2·h2yg(P,fM)=(∂2r2∂fM2·h2y+2∂r2∂fM∂h2y∂fM-r2h2y)·g-r2·h2y·∂2g∂fM2-∂∂fMr2·h2yg(P,fM)·2g·∂g∂fMg2(P,fM)]]>∂2∂fM2r2·h2zg(P,fM)=(∂2r2∂fM2·h2z+2∂r2∂fM∂h2z∂fM-r2h2z)·g-r2·h2z·∂2g∂fM2-∂∂fMr2·h2zg(P,fM)·2g·∂g∂fMg2(P,fM)]]>则其次，给出f1对P、fM的一阶偏导，二阶纯偏导，以及二阶混合偏导；因为χ0＝(2m-l2)P2+2klP-k2；∂a∂P=mk[(l2-2m)P2-k2]χ02;∂2a∂P2=2mk(2m-l2)2P3+3(2m-l2)Pk2+2k3lχ03]]>并且，设χ1=1-r1a(1-f);χ2=1-χ12;χ3=r1r2tanΔν2·1-cosΔνP;]]>χ4=r1r2tanΔν2(1-cosΔνP-1r1-1r2);∂2∂P21aP=4lm1P3-6km1P4;]]>φ1=arccos[1-r1a(1-f(P,fM))]+χ4aP;]]>φ2=r1r2(1-cosΔν)χ2·∂∂P1aP-χ3P·1ap+χ4·aP2·∂∂P1aP;]]>∂φ2∂P=k·∂2∂P21aP·[2-kaP]-(∂∂P1aP)2·[aP-k][kaP]12·[2-kaP]32+aP2·∂2∂P21aP+χ3·(1aPa·(km1P-lm)P2+12aP·∂∂P1aP)+χ4·141aP(P∂a∂P+a)·∂∂P1aP]]>所以设χ51＝χ61·2P2+χ62·2·P-2·r2·χ6·χ63；χ6＝r1-r1h2；χ61=(r1h2-r2)·∂r2∂fM+r2·r1ph2;χ63=χ6·∂r2∂fM-r2·r1ph2;]]>χ64=mkχ02;χ65=χ63-r2·χ6a·∂a∂fM;]]>χ7=r1-r1h2r1+r1h2;∂χ7∂fM=-r1·r1ph2(r1+r1h2)·sr12h2;]]>χ8=(r1-r1h2)·r2P-r2-r1;∂χ8∂fM=χ63P-∂r2∂fM;∂χ8∂P=-(r1-r1h2)·r2P2;]]>则∂f1∂fM=∂g∂fM+32aμ∂a∂fMarccos[1-r1a(P,fM)(1-f(P,fM))]+aμχ65Pχ2+∂a∂fM·χ7·χ8+a·∂χ7∂fMχ8+a·χ7·∂χ8∂fMμP---(36)]]>∂2f1∂P2=34gP2+32[121aμ(∂a∂P)2+aμ∂2a∂P2]·φ1+3aμ∂a∂P·φ2+a3μ·∂φ2∂P---(37)]]>因为所以因为χ9=∂2r2∂fM2χ6-2∂r2∂fMr1ph2+r2r1h2;χ10=1Pχ65χ2;∂χ2∂fM=χ1χ2·χ65aP]]>∂χ5∂fM=[2(∂r2∂fM)2+2r2∂2r2∂fM2]·sr12h22-8r2∂r2∂fMr1h2r1ph2+2r22(r1h22-r1ph22)]]>∂χ51∂fM[2r1ph2∂r2∂fM+(r1h2-r2)·∂2r2∂fM2-r2·r1h2-(∂r2∂fM)2]·2P2-2χ632-2r2χ6χ9+{[2(∂r2∂fM)2+(r1+2r2)·∂2r2∂fM2]·χ6-2(r1+2r2)∂r2∂fMr1ph2+(r1r2+r22)r1h2}·2P]]>∂2a∂fM2=P·(∂χ5∂fM·1χ0-χ64·∂χ51∂fM-2·χ5χ51χ02+2χ64χ512χ0)]]>∂χ10∂fM=1P·{∂2r2∂fM2·χ6-2∂r2∂fMr1ph2+r2r1h2-[r2a∂2a∂fM2+1a∂a∂fM∂r2∂fM-r2a2(∂a∂fM)2]·χ6+r2a∂a∂fMr1ph2}·χ2-χ65·∂χ2∂fMχ22]]>∂2χ7∂fM2=r1r1h2·[r1+(r1xh2x+r1yh2y+r1zh2z)]sr12h2+r1·r1ph2·{r1ph2sr12h2-[r1+(r1xh2x+r1yh2y+r1zh2z)]r1h2r1ph2sr12h2}[r1+(r1xh2x+r1yh2y+r1zh2z)]2sr12h22]]>∂2χ8∂fM2=χ9P-∂2r2∂fM2]]>所以∂2f1∂fM2=∂2g∂fM2+12a∂a∂fM{32aμ∂a∂fMarccos[1-r1a(P,fM)(1-f(P,fM))]+aμχ65Pχ2}+aμ{32∂2a∂fM2arccos[1-r1a(P,fM)(1-f(P,fM))]-32∂a∂fMχ10a+∂χ10∂fM}+∂2a∂fM2χ7χ8+a∂2χ7∂fM2χ8+aχ7∂2χ8∂fM2+2∂a∂fM∂χ7∂fMχ8+2∂a∂fMχ7∂χ8∂fM+2a∂χ7∂fM∂χ8∂fMμP---(39)]]>最后，给出f2对fM的一阶偏导，二阶偏导；因为∂E∂fM=21+eM1-eM[1+cos(fM)]+1-eM1+eM[1-cos(fM)]]]>∂2E∂fM2=2{1+eM1-eM[1+cos(fM)]+1-eM1+eM[1-cos(fM)]}sin(fM)·(1+eM1-eM-1-eM1+eM)]]>所以∂2f2∂fM2=∂2E∂fM2[1-eMcos(E)]+eMsin(E)·(∂E∂fM)2---(41)]]>至此，由公式(30)至公式(41)，并结合公式(26)和公式(27)，获得公式(22)的解析表达式，算法完整执行。本发明以Kepler轨道理论以及基于P迭代法的Gauss问题为基础，将目标存在轨道机动的拦截变轨最小速度修正问题，转化为最优规划问题，并通过最优规划理论获得了与Δvmin对应的KKT条件，同时为快速求解KKT条件，进一步地设计了牛顿迭代，获得了解析的梯度信息。相对于一般的搜索算法，该方法计算精度高，速度快，且对初值不敏感。通过对比试验，采用一种基于半分法的加速搜索算法，虽然该基于半分法的加速搜索算法相对于一般的遍历式搜索算法，其计算效率得到大幅提高，但依然是本发明耗时的30倍。本发明也和MATLAB自带的优化函数fmincon进行了对比，结果也表明无论是计算精度还是计算速度，本文的算法都更具有优势。附图说明图1是Gauss问题示意图。图2是目标有轨道机动的，基于最小速度修正量的拦截器交战示意图。图3是简化的目标存在轨道机动的拦截变轨最小速度修正问题示意图。图4是采用半分法的传统求解流程图。图5是本发明中方法的计算流程图。具体实施方式需要说明的是，在不冲突的情况下，本申请中的实施例及实施例中的特征可以相互组合。下面请参考附图并结合实施例来详细说明本发明。对于求解目标存在轨道机动的快速确定能量最优拦截预测命中点的数值优化方法，也就是拦截变轨最小速度修正问题，一定存在一个最优的拦截时间t，使得目标与拦截弹经过时间t后，同时抵达最优拦截位置r2，并且使拦截弹在初始位置r1处的速度改变量最小。所以，本质上拦截时间t是最小速度修正问题的唯一自变量，但是公式推导过于复杂。在公式(9)与公式(11)，其中的变量P与变量fM，分别是求解Gauss问题与求解终端位置矢量r2过程中的重要迭代变量。将最小速度修正问题的自变量扩展至X＝[tPfM]T；同时结合公式(9)与公式(11)，引入两组等式约束f1=g+a3μ{arccos[1-r1a(1-f)]+r1r2f·μa}-t]]>f2=EM(fM)-eMsin[EM(fM)]-2πTM(t-tpM)]]>使拦截弹的速度修正量最小，描述为数学表达式，则目标函数为J(X)＝(v1x-v0x)2+(v1y-v0y)2+(v1z-v0z)2至此，把目标存在轨道机动的拦截变轨最小速度修正问题，转化为一个含有等式约束的最优规划问题，该最优规划问题的表达式整理如下X＝[tPfM]TJ(X)＝(v1x-v0x)2+(v1y-v0y)2+(v1z-v0z)2f1(t,P,fM)=g+a3μ{arccos[1-r1a(1-f)]+r1r2f·μa}-t---(13)]]>f2(t,fM)=EM(fM)-eMsin[EM(fM)]-2πTM(t-tpM)]]>设带有Lagrange乘子的增广目标函数为L＝J+λ1f1+λ2f2(14)由KKT条件，可得∂L∂t=λ1-2πTMλ2=0---(15)]]>∂L∂P=∂J∂P+λ1∂f1∂P=0---(16)]]>∂L∂fM=∂J∂fM+λ1∂f1∂fM+λ2∂f2∂fM=0---(17)]]>由公式(15)与(16)，可以解得λ1=-∂J/∂P∂f1/∂Pλ2=-TM2πλ1=TM2π∂J/∂P∂f1/∂P---(18)]]>将公式(18)代入公式(17)，可以得到等式f3(P,fM)=∂J∂fM-∂J/∂P∂f1/∂P∂f1∂fM+TM2π∂J/∂P∂f1/∂P∂f2∂fM---(19)]]>所以，KKT条件最终转化为三个等式约束f1(t,P,fM)=0f2(t,fM)=0f3(P,fM)=0---(20)]]>设F(X)＝[f1f2f3]T(21)则方程组(21)的解就是拦截变轨最小速度修正问题的最优解。以下介绍如何设计牛顿迭代求解方程组(21)。方程组F(X)的Jacobi矩阵是F′(X)=∂f1∂t∂f1∂P∂f1∂fM∂f2∂t0∂f2∂fM0∂f3∂P∂f3∂fM---(22)]]>其中，因为f2中不显含P，f3中不显含t，所以则自变量X的迭代公式可以写为XK+1＝XK-[F′(XK)]-1·F(XK)(23)为提高数值计算的稳定性，可以利用系数矩阵u和v，将公式(22)转化为公式(24)FF′(X)=abc·F′(X)·def=u·F′(X)·v---(24)]]>其中，对角阵u和v，分别称为F(X)量级统一的系数矩阵，以及变量X归一化的系数矩阵。进一步地，迭代公式(23)可以转化为XXK=v-1·XKXXK+1=XXK-[FF′(XK)]-1·u·F(XK)---(25)]]>至此，可以将本发明的快速确定能量最优拦截预测命中点的数值优化方法阐述为：1、给定自变量X的试探值，并设定系数矩阵u和v；2、由公式(22)和公式(24)计算偏导数矩阵FF′(X)；3、由公式(25)计算新的自变量取值Xk+1。4、判断是否收敛。如果ΔXX＝XXk+1-XXk小于误差限，计算结束；否则转至步骤2。本发明的方法实现了对Δvmin的快速求解，同时也求解出最优拦截位置与拦截时间。该算法计算精度高，速度快，且对初值不敏感。计算流程图如图5所示。以下整理公式(22)中，各项的解析表达式。因为∂f3∂P=∂2J∂P∂fM+∂2J∂P2·∂f1∂P-∂J∂P·∂2f1∂P2(∂f1∂P)2·(TM2π∂f2∂fM-∂f1∂fM)-∂J/∂P∂f1/∂P·∂2f1∂P∂fM∂f3∂fM=∂2J∂fM2+∂2J∂P∂fM·∂f1∂P-∂J∂P·∂2f1∂P∂fM(∂f1∂P)2·(TM2π∂f2∂fM-∂f1∂fM)∂J/∂P∂f1/∂P·(TM2π∂2f2∂fM2-∂2f1∂fM2)---(26)]]>并且，显然所以，只需获得J、f1、f2对P、fM的一阶偏导，二阶纯偏导，以及二阶混合偏导，即可获得公式(22)的解析表达式。将矢量投影在大地直角坐标系，并约定h2xh2yh2z=cos(fM+w)cosΩ-sin(fM+w)cosisinΩcos(fM+w)sinΩ+sin(fM+w)cosicosΩsin(fM+w)sini---(28)]]>则首先，给出J对P、fM的一阶偏导，二阶纯偏导，以及二阶混合偏导。设JPy1=r2y(fM)g(P,fM)-r1yf(P,fM)g(P,fM)-v0y;JPy2=r2y(fM)-r1y[2-f(P,fM)]2·P·g(P,fM);]]>JPz1=r2z(fM)g(P,fM)-r1zf(P,fM)g(P,fM)-v0z;JPz2=r2z(fM)-r1z[2-f(P,fM)]2·P·g(P,fM);]]>r1h2＝r1xh2x+r1yh2y+r1zh2z；sr12h2=r12-(r1xh2x+r1yh2y+r1zh2z)2]]>则因为∂r2∂fM=r2·eM·sin(fM)1+eM·cos(fM)]]>∂h2x∂fM∂h2y∂fM∂h2z∂fM=-sin(fM+w)cosΩ-cos(fM+w)cosisinΩ-sin(fM+w)sinΩ+cos(fM+w)cosicosΩcos(fM+w)sini]]>∂g∂fM=1μP·[∂r2∂fM·sr12h2-r2·rph2·r1h2sr12h2]]]>∂f∂fM=1P[∂r2∂fM(cosΔν-1)+r2·r1ph2r1]]]>∂∂fMf(P,fM)g(P,fM)=∂f∂fM·g-f·∂g∂fMg2]]>所以，设∂γMr2x(fM)g(P,fM)=(∂r2∂fM·h2x+r2·∂h2x∂fM)g-r2·h2x·∂g(P,fM)∂fMg2(P,fM);JfMx2=∂∂fMr2x(fM)g(P,fM)-r1x·∂∂fMf(P,fM)g(P,fM)]]>∂∂fMr2y(fM)g(P,fM)=(∂r2∂fM·h2y+r2·∂h2y∂fM)g-r2·h2y·∂g(P,fM)∂fMg2(P,fM);JfMy2=∂∂fMr2y(fM)g(P,fM)-r1y·f(P,fM)g(P,fM)]]>∂∂fMr2z(fM)g(P,fM)=(∂r2∂fM·h2z+r2·∂h2z∂fM)g-r2·h2z·∂g(P,fM)∂fMg2(P,fM);JfMz2=∂∂fMr2z(fM)g(P,fM)-r1z·∂∂fMf(P,fM)g(P,fM)]]>则∂J∂fM=2·(JPx1·JfMx2+JPy1·JfMy2+JPz1·JfMz2)---(31)]]>∂2J∂P2=-12P∂J∂P+2·(JPx22+JPy22+JPz22)+1Pg∂f∂P·(JPx1·r1x+JPy1·r1y+JPz1·r1z)---(32)]]>因为所以因为∂2h2x∂fM2∂2h2y∂fM2∂2h2z∂fM2T=-h2xh2yh2zT]]>∂2g∂fM2=1μP[∂2r2∂fM2sr12h2-2·∂r2∂fMr1ph2·r1h2sr12h2-r2·(r1ph22-r1h22)·r12+r1h24sr12h23]]]>∂2f∂fM2=1r1P[2·∂r2∂fM·r1ph2-r2·r1h2-∂2r2∂fM2·(r1-r1h2)]]]>∂2∂fM2f(P,fM)g(P,fM)=∂2f∂fM2g-f∂2g∂fM2-2∂f∂fM∂g∂fM+2fg(∂g∂fM)2g2]]>所以，设∂2∂fM2r2·h2xg(P,fM)=(∂2r2∂fM2·h2x+2∂r2∂fM∂h2x∂fM-r2h2x)·g-r2·h2x·∂2g∂fM-∂2∂fMr2·h2xg(P,fM)·2g·∂g∂fMg2(P,fM)]]>∂2∂fM2r2·h2yg(P,fM)=(∂2r2∂fM2·h2y+2∂r2∂fM∂h2y∂fM-r2h2y)·g-r2·h2y·∂2g∂fM2-∂∂fMr2·h2yg(P,fM)·2g·∂g∂fMg2(P,fM)]]>∂2∂fM2r2·h2zg(P,fM)=(∂2r2∂fM2·h2z+2∂r2∂fM∂h2z∂fM-r2h2z)·g-r2·h2z·∂2g∂fM2-∂∂fMr2·h2zg(P,fM)·2g·∂g∂fMg2(P,fM)]]>则∂2J∂fM2=2·JfMx22+JPx1·[∂2∂fM2r2·h2xg(P,fM)-r1x∂2∂fM2f(P,fM)g(P,fM)]+JfMy22+JPy1·[∂2∂fM2r2·h2yg(P,fM)-r1y∂2∂fM2f(P,fM)g(P,fM)]+JfMz22+JPz1·[∂2∂fM2r2·h2zg(P,fM)-r1z∂2∂fM2f(P,fM)g(P,fM)]---(34)]]>其次，给出f1对P、fM的一阶偏导，二阶纯偏导，以及二阶混合偏导。因为χ0＝(2m-l2)P2+2klP-k2；∂a∂P=mk[(l2-2m)P2-k2]χ02;∂2a∂P2=2mk(2m-l2)2P3+3(2m-l2)Pk2+2k3lχ03]]>并且，设χ1=1-r1a(1-f);χ2=1-χ12;χ3=r1r2tanΔν2·1-cosΔνP;]]>χ4=r1r2tanΔν2(1-cosΔνP-1r1-1r2);∂2∂P21aP=4lm1P3-6km1P4;]]>φ1=arccos[1-r1a(1-f(P,fM))]+χ4aP;]]>φ2=r1r2(1-cosΔν)χ2·∂∂P1aP-χ3P·1aP+χ4·aP2·∂∂P1aP;]]>∂φ2∂P=k·∂2∂P21aP·[2-kaP]-(∂∂P1aP)2·[aP-k][kaP]12·[2-kaP]32+aP2·∂2∂P21aP+χ3·(1aPa·(km1P-lm)-2P2+12aP·∂∂P1aP)+χ4·141aP(P∂a∂P+a)·∂∂P1aP]]>所以设χ51＝χ61·2P2+χ62·2·P-2·r2·χ6·χ63；χ6＝r1-r1h2；χ61=(r1h2-r2)·∂r2∂fM+r2·r1ph2;χ63=χ6·∂r2∂fM-r2·r1ph2;]]>χ64=mkχ02;χ65=χ63-r2·χ6a·∂a∂fM;]]>χ7=r1-r1h2r1+r1h2;∂χ7∂fM=-r1·r1ph2(r1+r1h2)·sr12h2;]]>χ8=(r1-r1h2)·r2P-r2-r1;∂χ8∂fM=χ63P-∂r2∂fM;∂χ8∂P=-(r1-r1h2)·r2P2;]]>则，∂f1∂fM=∂g∂fM+32aμ∂a∂fMarccos[1-r1a(P,fM)(1-f(P,fM))]+aμχ65Pχ2+∂a∂fM·χ7·χ8+a·∂χ7∂fMχ8+a·χ7·∂χ8∂fMμP---(36)]]>∂2f1∂P2=34gP2+32[121aμ(∂a∂P)2+aμ∂2a∂P2]·φ1+3aμ∂a∂P·φ2+a3μ·∂φ2∂P---(37)]]>因为所以∂2f1∂P∂fM=-12P∂∂fMg(P,fM)-1P1χ2aμ·χ63·(1P+∂χ2∂P1χ2)+12a∂a∂P·{32aμ∂a∂fMarccos[1-r1a(P,fM)(1-f(P,fM))]+aμχ65Pχ2}+32aμ{∂2a∂P∂fMarccos[1-r1a(P,fM)(1-f(P,fM))]+∂a∂fMkχ2·∂∂P1aP}-aμr2χ6[(∂∂P1aP∂a∂fM+1aP∂2a∂P∂fM)-1χ2-1aPχ22∂a∂fM∂χ2∂P]---(38)]]>因为χ9=∂2r2∂fM2χ6-2∂r2∂fMr1ph2+r2r1h2;χ10=1Pχ65χ2;∂χ2∂fM=χ1χ2·χ65aP]]>∂χ5∂fM=[2(∂r2∂fM)2+2r2∂2r2∂fM2]·sr12h22-8r2∂r2∂fMr1h2r1ph2+2r22(r1h22-r1ph22)]]>∂χ51∂fM[2r1ph2∂r2∂fM+(r1h2-r2)·∂2r2∂fM2-r2·r1h2-(∂r2∂fM)2]·2P2-2χ632-2r2χ6χ9+{[2(∂r2∂fM)2+(r1+2r2)·∂2r2∂fM2]·χ6-2(r1+2r2)∂r2∂fMr1ph2+(r1r2+r22)r1h2}·2P]]>∂2a∂fM2=P·(∂χ5∂fM·1χ0-χ64·∂χ51∂fM-2·χ5χ51χ02+2χ64χ512χ0)]]>∂χ10∂fM=1P·{∂2r2∂fM2·χ6-2∂r2∂fMr1ph2+r2r1h2-[r2a∂2a∂fM2+1a∂a∂fM∂r2∂fM-r2a2(∂a∂fM)2]·χ6+r2a∂a∂fMr1ph2}·χ2-χ65·∂χ2∂fMχ22]]>∂2χ7∂fM2=r1r1h2·[r1+(r1xh2x+r1yh2y+r1zh2z)]sr12h2+r1·r1ph2·{r1ph2sr12h2-[r1+(r1xh2x+r1yh2y+r1zh2z)]r1h2r1ph2sr12h2}[r1+(r1xh2x+r1yh2y+r1zh2z)]2sr12h22]]>∂2χ8∂fM2=χ9P-∂2r2∂fM2]]>所以∂2f1∂fM2=∂2g∂fM2+12a∂a∂fM{32aμ∂a∂fMarccos[1-r1a(P,fM)(1-f(P,fM))]+aμχ65Pχ2}+aμ{32∂2a∂fM2arccos[1-r1a(P,fM)(1-f(P,fM))]-32∂a∂fMχ10a+∂χ10∂fM}+∂2a∂fM2χ7χ8+a∂2χ7∂fM2χ8+aχ7∂2χ8∂fM2+2∂a∂fM∂χ7∂fMχ8+2∂a∂fMχ7∂χ8∂fM+2a∂χ7∂fM∂χ8∂fMμP---(39)]]>最后，给出f2对fM的一阶偏导，二阶偏导。因为∂2E∂fM2=2{1+eM1-eM[1+cos(fM)]+1-eM1+eM[1-cos(fM)]}2sin(fM)·(1+eM1-eM-1-eM1+eM)]]>所以∂2f2∂fM2=∂2E∂fM2[1-eMcos(E)]+eMsin(E)·(∂E∂fM)2---(41)]]>至此，由公式(30)至公式(41)，并结合公式(26)和公式(27)，可以获得公式(22)的解析表达式，方法可以完整执行。结合图2中的注释，对一种可能的交战情形作如下描述：t1时刻，拦截器E的位置矢量与速度矢量分别是并且，如果拦截器与目标均不进行任何机动，二者将在P1点碰撞。此时，目标M进行轨道机动，新的轨道根数为[Ω,i,aM,eM,ω,tpM]＝[1.25442346395840,1.31152621076928,5319700.61120683,0.516254059012830,4.56809019516139,1959.60308392449]；轨道的运行周期TM＝3861.3607137952。则拦截器需要将速度v0修正至合适的速度v1，才能在最小燃料消耗，即最小速度修正量的前提下，在新的目标轨道上拦截目标M。以上是问题的初始条件，因为本发明在推导过程中，已经将该工程问题转化为带有等式约束的最优规划问题，所以在与传统的搜索方法进行对比的同时，也将与MATLAB软件自带的求解函数fmincon进行对比。状态量X＝[tPfM]T的上下限分别设为Xmin＝[tminPminfMmin]T＝[1001e6-π]TXmax＝[tmaxPmaxfMmax]T＝[8005e6π]T本发明和fmincon迭代初值的选取规则为：t0＝(tmin+tmax)/2；P0沿用拦截器E变轨前的轨道半通径；fM0通过将t0代入公式(11)求解获得。所以，该算例的初值为X0＝[t0P0fM0]＝[4502.4473e6-2.8802]将初值X0代入迭代公式(25)中，完成求解。全部的仿真程序在CPU为I5-2410M，主频2.3GHz的个人计算机中以及MATLAB2014a仿真环境下完成，更高效的编译环境将提高计算效率。表1是不同方法的计算结果对比。表1不同方法的计算精度对比可以看出，虽然三种方法的计算结果以及目标函数的最小值基本都是一致的，但是把计算结果代入KKT条件(20)，会发现搜索法的结果不能很好地满足KKT条件，所以它的计算精度远低于本发明的方法。其次，我们比较三种算法的计算效率，基于半分法的加速搜索算法的计算效率虽然远高于fmincon，但是本发明的计算方法可以进一步将耗时从13.47毫秒压缩至0.490毫秒，计算效率大约提高27.5倍。表2是基于半分法的加速搜索迭代过程表2搜索法的迭代过程次数t(s)P(m)fM(rad)ΔV(m/s)14501.1307e6-2.88021698.384922757.8614e6-2.99123698.53613362.52.9945e6-2.9364780.79294406.251.8565e6-2.9085937.52835384.3752.3607e6-2.9225670.65566373.43752.6593e6-2.9294665.82087378.90632.5057e6-2.9260653.23588376.17192.5814e6-2.9277655.62999377.53912.5433e6-2.9268653.466810378.22272.5244e6-2.9264653.111811378.56452.5150e6-2.9262653.114212378.39362.5197e6-2.9263653.098113378.30812.5221e6-2.9263653.101214378.35082.5209e6-2.9263653.098715378.37222.5203e6-2.9263653.098216378.38292.5200e6-2.9263653.0981表3是本发明的迭代过程。表3本发明的迭代过程次数t(s)P(m)fM(rad)ΔV(m/s)14502.4473e6-2.8802333.77812377.39692.5651e6-2.9275655.31643378.38542.5196e6-2.9263653.14844378.38632.5199e6-2.9263653.09815378.38662.5199e6-2.9263653.0981综上，本发明基于最优规划理论，通过对拦截变轨最小速度修正问题进行数学建模，经过大量的公式推导，获得了Δvmin对应的KKT条件，并通过设计牛顿迭代算法，获得了解析的梯度信息，实现了对Δvmin的快速求解，同时也求解出最优拦截位置与拦截时间。经过比对验证，该算法计算精度更高，速度更快。当前第1页1 2 3