一种基于贝叶斯理论和气垫船姿态信息的海浪信息预测方法与流程

本发明涉及的是一种海浪信息预测方法，具体地说是一种基于贝叶斯理论的海浪信息预测在气垫船上的应用。

背景技术：

气垫船作为水陆两栖的船种，能够在水面和地面上方便地航行，因此其用途十分广泛。气垫船分为全垫升气垫船和侧壁式气垫船，本发明主要针对全垫升气垫船。气垫船由于其快速性，在海面上航行主要受海浪和海风的影响。因此，获得其航行海域的实时海况具有重要意义。

针对气垫船的作业特点，获取实时的海况信息十分困难，传统的获取海况信息的方法为定点测量法，无法满足气垫船的作业需求。而随船估计法，将气垫船的本身在海上的姿态运动与海浪的运动看作一种线性关系，通过获取气垫船实时姿态信息来反演海况信息。原理与浮标法相似，将气垫船本身近似看作浮标，由于气垫船大多为小型船舶，从而此种近似比其他船舶近似性要好。

在对国内外的公开文献进行检索分析之后，未找到降本发明的方法应用到气垫船中的公开报道。

技术实现要素：

本发明的目的在于提供一种能够得到气垫船航行海域的实时海况信息的基于贝叶斯理论和气垫船姿态信息的海浪信息预测方法。

本发明的目的是这样实现的：

步骤一、根据固定坐标系和船体运动坐标系，对气垫船建立六自由度运动数学模型；

步骤二、基于步骤一中建立的运动数学模型仿真气垫船的横摇、纵摇和升沉三自由度姿态信息；利用多元预测理论对气垫船运动三自由度姿态信息进行交叉谱分析，得到交叉谱；

步骤三、利用气垫船实物仿真实验获取气垫船的响应幅度算子函数；

步骤四、将步骤二中得到的交叉谱和步骤三中得到的响应幅度算子函数作为贝叶斯模型的输入，并利用贝叶斯模型反演航行海域的实时海况。

本发明还可以包括：

1、所述对气垫船建立六自由度运动数学模型包括运动学数学模型和动力学数学模型。

2、所述交叉谱分析的具体过程为：

针对每个时间序列zi，使用前p个时间序列值对第s个时间序列进行建模：

zi(s)-A1zi(s-1)-…-Apzi(s-p)＝εi i＝1,2,…,k

其中，Ai为权重系数；εi为均值为0方差为σi的高斯白噪声，代表测得值与模型估计值之间的误差；

同时考虑所有时间序列改为如下矩阵形式：

Ζ(s)-A1Ζ(s-1)-…-ApΖ(s-p)＝ε(s)

其中，Ai为k×k维的权重系数矩阵；ε(s)＝[ε1,ε2,…,εk]^T为均值为0方差为σi的高斯白噪声序列，考虑εi与前面的z(s)值无关，从而ε(s)与ε(s-p)之间的协方差为零，因此，白噪声向量的协方差矩阵如下：

其中，σij为εi与εj协方差；

进一步改写为如下形式：

采用whittle递推法计算多维AR(p)模型的系数矩阵：

令：Λpj＝(Ap1 Ap2 … Apj)；j＝1,2,…,p；

令Ri，i＝1…P为相关矩阵，针对不同的延迟l＝1…L相关矩阵中的第i,j元素的计算公式如下：

递推公式为：

由递推公式多维AR(p)系数矩阵的计算步骤为：

i.首先对船舶响应运动数据进行均值化处理；

ii.计算相关矩阵Ri，i＝0,1,…,p；

iii.由递推公式计算A11，B11，然后计算A22，B22和A21，B21，···以此类推，计算出App…Ap1和Bpp…Bp1，再计算Ap+1,p+1，Bp+1,p+1；

通过以上步骤求得Λp；p＝1…P共计P组权重系数矩阵，通过阶数判别准则选用哪一组。

3、所述利用贝叶斯模型反演航行海域的实时海况具体过程为：

根据测得的船舶运动响应时间序列计算得到相应的交叉谱Φij(ωe,β)是遭遇频率ωe和遭遇角β的函数，

假定船舶响应与实时海浪成线性关系，船舶响应RAO(ωe,β)函数与交叉谱φij(ωe)之间的关系为：

令α＝0，即β＝θ，转化为：

求解E(ωe,β)的过程称为反卷积过程，解决反卷积问题用Bayesian模型方法，

一个未知的物理过程u(x)，且u(x)由N组测得的数据ci解算出，即满足：

ci＝∫ri(x)u(x)dx+ei；i＝1,2,…,N

u(x)和ci通过一个核函数ri(x)，并且考虑测量误差ei，考虑要解算的变量为xi；i＝1,2,…,M，且M要比N大，矩阵形式如下：

c＝Ru+e

采用最小二乘法进行解算：

minχ²(u)＝min||Ru-c||²

其中，χ²＝||·||表示矩阵2-范数；

基于最小二乘法，取下式最小值：

χ²(u)＝||Ru-c||²

系统是奇异系统，取下式的最小值：

χ²(u)+μ||u-u0||²

u0表示指定的参数向量，包含问题的先验信息；μ是超参数是大于零的常数，最小值由求下式的最大值取得：

其中，假定方差σ²暂时已知，

数据分布：

先验分布：

考虑到(μ,σ²)的边缘似然函数：

P(μ,σ²)＝∫f(c|σ²,u)π(u|μ,σ²)du

这里需要求解μ和σ²的最优值。

多元模型表达式的最终形式如下：

b＝Af(x)+w

其中，A由响应幅度算子函数RAO构成；b由交叉谱构成；w为高斯白噪声；f(x)为待求海浪方向谱函数。

本发明的效果主要包括：

1、本发明所述的是一种根据气垫船在海上的运动姿态数据来反推航行海域的海况信息的方法；

2、本发明所述的贝叶斯模型输出的是离散化的海浪方向谱函数值，解决了参数法带来的运算复杂度的问题。

附图说明

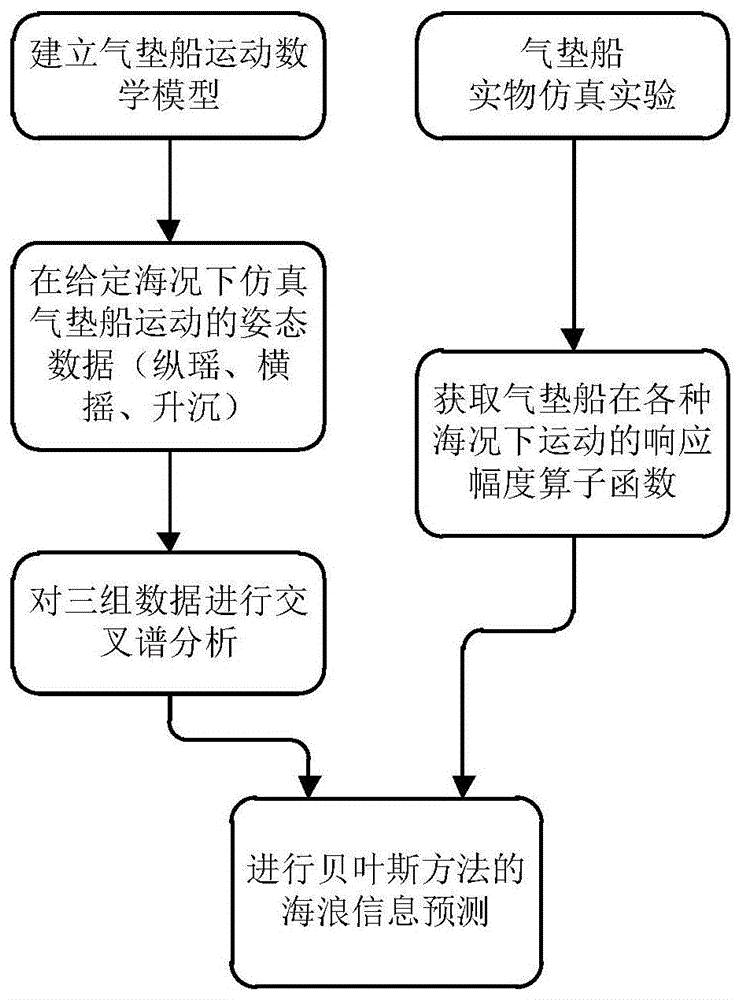
图1为本发明的流程图；

图2为某船型在某种海况下的三自由度响应运动曲线图；

图3为某船型在某海况下的横摇和纵摇的交叉谱函数曲线；

图4为某船型的在特定遭遇角下的三自由度响应运动幅度算子函数；

图5为某气垫船在某海况下的海况估计曲线图。

具体实施方式

下面举例对本发明做更详细的描述。

结合图1，本发明的方法主要包括如下步骤：

一、建立气垫船运动数学模型：

建立固定坐标系和船体运动坐标系，对气垫船建立六自由度运动数学模型；

二、获取气垫船的姿态参数，并对姿态数据进行交叉谱分析：

基于步骤一中建立的运动模型仿真气垫船的横摇，纵摇和升沉三自由度姿态信息；利用多元预测理论对气垫船运动三自由度姿态数据进行谱分析，得到交叉谱；

三、获取气垫船运动响应幅度算子函数：

根据气垫船实物仿真实验获取气垫船的响应幅度算子函数；

四、利用贝叶斯理论对气垫船航行海域海况进行实时预测：

将步骤二中得到的三自由度运动数据的交叉谱和步骤三中得到的响应幅度算子函数作为贝叶斯模型的输入，并利用贝叶斯理论反演航行海域的实时海况。

步骤一中所述的建立气垫船六自由度运动数学模型，包括运动学数学模型和动力学数学模型；基于气垫船运动数学模型仿真气垫船在特定海况下的横摇、纵摇和升沉三个自由度运动数据。利用多元预测理论对气垫船运动三自由度姿态数据进行谱分析，得到横摇、纵摇和升沉三自由度的交叉谱数；交叉谱分析的具体过程为：

针对每个时间序列，使用前p个时间序列值对第s个时间序列进行建模：

zi(s)-A1zi(s-1)-…-Apzi(s-p)＝εi i＝1,2,…,k

其中，Ai为权重系数；εi为均值为0方差为σi的高斯白噪声，代表测得值与模型估计值之间的误差。

同时考虑所有时间序列，那么模型可改写为如下矩阵形式：

Ζ(s)-A1Ζ(s-1)-…-ApΖ(s-p)＝ε(s)

其中，Ai为k×k维的权重系数矩阵；ε(s)＝[ε1,ε2,…,εk]^T为均值为0方差为σi的高斯白噪声序列，考虑εi与前面的z(s)值无关，从而ε(s)与ε(s-p)之间的协方差为零，因此，白噪声向量的协方差矩阵如下：

其中，σij为εi与εj协方差。

方便起见，模型改写为如下形式：

采用whittle递推法计算多维AR(p)模型的系数矩阵：

为了表示多维AR(p)模型的系数Aj(j＝1,2,…,p)随着模型阶数p的变化而变化，令：Λpj＝(Ap1 Ap2 … Apj)；j＝1,2,…,p。

令Ri(i＝1…P)为相关矩阵，针对不同的延迟l(这里延迟范围为l＝1…L)相关矩阵中的第i,j元素的计算公式如下：

那么，递推公式如下：

由递推公式可知，多维AR(p)系数矩阵的计算步骤为：

iv.由于多维AR(p)模型建模的前提是零均值平稳随机过程，所以首先要对船舶响应运动数据进行均值化处理。

v.计算相关矩阵Ri(i＝0,1,…,p)。

vi.由递推公式计算A11，B11，然后计算A22，B22和A21，B21，···以此类推，计算出App…Ap1和Bpp…Bp1，再计算Ap+1,p+1，Bp+1,p+1。

通过以上步骤能够求得Λp；p＝1…P共计P组权重系数矩阵，究竟选用哪一组作为多维AR(p)模型的最终系数矩阵，要通过阶数判别准则来确定。

步骤三中所述，对选定气垫船进行实物实验得出相应的响应幅度算子函数，响应运动幅度算子函数与气垫船本身形状相关，一旦实验得出，其函数形式是固定不变的；

步骤五中所述，建立海浪预测的贝叶斯数学模型，将响应幅度算子函数和三自由度运动数据的交叉谱作为贝叶斯模型的输入，并利用贝叶斯理论反演航行海域的实时海况，具体过程为：

根据测得的船舶运动响应时间序列计算得到相应的交叉谱Φij(ωe,β)是遭遇频率ωe和遭遇角β的函数。

假定船舶响应与实时海浪成线性关系，那么船舶响应RAO(ωe,β)函数与交叉谱φij(ωe)之间有如下关系成立：

方便起见，令α＝0，即β＝θ，可转化为：

上式表明，方向谱函数E(ωe,β)与船舶响应函数RAO(ωe,β)的乘积的对遭遇角β的积分等于其交叉谱值。因而，估计海浪方向谱的过程属于一种逆过程，求解E(ωe,β)的过程称为反卷积过程。解决反卷积问题一般用Bayesian模型方法。

一般情况下，研究一个未知的物理过程u(x)，且u(x)可由N组测得的数据ci解算出，即满足：

ci＝∫ri(x)u(x)dx+ei；i＝1,2,…,N

u(x)和ci通过一个核函数ri(x)，并且考虑测量误差ei。考虑要解算的变量为xi；i＝1,2,…,M，且M要比N大得多，那么矩阵形式如下：

c＝Ru+e

可以采用最小二乘法进行解算：

minχ²(u)＝min||Ru-c||²

其中，χ²＝||·||表示矩阵2-范数。

基于最小二乘法，取下式最小值：

χ²(u)＝||Ru-c||²

如前面提到的，系统一般情况下是奇异系统，取下式的最小值：

χ²(u)+μ||u-u0||²

式中，u0表示指定的参数向量，它包含问题的先验信息；μ是超参数(大于零的常数)。然而，这种思想带来了新的问题——超参数的选取。原式的最小值可由求下式的最大值取得：

其中，假定方差σ²暂时已知。

数据分布：

先验分布：

考虑到(μ,σ²)的边缘似然函数：

P(μ,σ²)＝∫f(c|σ²,u)π(u|μ,σ²)du

这里需要求解μ和σ²的最优值。

多元模型表达式的最终形式如下：

b＝Af(x)+w

其中，A由响应幅度算子函数RAO构成；b由交叉谱构成；w为高斯白噪声；f(x)为待求海浪方向谱函数。

本发明中采用的是三自由度气垫船动响应数据，那么多维AR(p)模型即为三维模型可化简为如下形式：

其中，N为数据序列长度；Roll为横摇数据序列；Pitch为纵摇数据序列；Heave为升沉数据序列。应用多维AR(p)模型的前提条件：序列应是零均值平稳随机过程，首先应对各个序列进行零均值化处理。其次，按照权利要求书中所叙述的步骤进行多维AR(p)模型系数的推导，具体实现即将序列维数定为三维。

步骤四中利用贝叶斯理论估计海况信息的具体过程为：

基于贝叶斯模型：

b＝Af(x)+w

的具体解算过程如下：

1.首先引入两个概率分布：

(1)数据分布

根据假定的w为零均值，σ²方差的高斯分布，交叉谱数据的似然函数可通过多元高斯分布给出：

其中，||||代表矩阵的2-范数；N²·L是方程的总个数，N是数据的维数，L是遭遇频率的个数。

(2)先验分布

假定海浪方向谱E(ω,β)为每个离散区域ΔβΔω上的能量分段常值，并没有考虑各个值之间的关系。实际上，海浪方向谱函数应是一个平滑连续的函数。这样就可以以先验分布的形式引入附加条件。因此，可通过海浪方向谱函数E(ω,β)的二阶导建立先验分布：

其中，M和K分别为海浪频率和离散个数和遭遇角的离散个数。

为避免在频率边缘处出现过估计问题，引入先验分布：

其中，x0为初始值。

在以上假设的基础上，并且认为两个先验分布都服从零均值，方差为的高斯分布，那么整体先验分布可整理为如下矩阵形式：

矩阵D由下面矩阵构成。由向量x的形式确定矩阵D的形式为：

其中，D1形式如下：

式中，形式如下：

D2形式如下：

其中：

D3形式如下：

其中，1为如上所述K×K的单位阵。

D4形式如下：

同时，向量c形式如下：

其中，x0位于向量的最后K·M行中，x0为初值。

2.求解模型：

根据贝叶斯理论，海浪谱的后验分布由数据分布和先验分布组成：

p(x|σ²,μ)∝l(x|σ²)·p(x|μ,σ²)

即：

其中：

S(x)＝||Af(x)-b||²+μ²||Dx-c||²

显然，对于给定的b，σ²和μ来讲，后验分布x的最大值可通过计算S(x)的最小值获得。

由于指数函数的引入，导致f(x)的非线性，这里在x0处使用泰勒展开进行线性化，f(x)线性化后为：

f(x)＝f(x0)+F(x0)(x-x0)

其中，F(x)为(K·M)×(K·M)维对角阵：

得：

S(x)＝||A^*x-b^*||²+μ²||Dx-c||²

其中，

A^*＝AF(x0)

b^*＝b-Af(x0)-A^*F(x0)x0

那么，S(x)可整理为最终的形式：

S(x)＝||Gx-d||²

其中，

继续采用最小二乘法迭代结计算即可。

由于模型中的待求参数远远多于实际方程的个数，系统方程存在不确定性，并且不能够通过一般的多元过程解决其不确定性，通过Bayesian方法的引入，从而解决模型参数的计算问题。而待求参数恰好为海浪方向谱的各个离散点的值，故从而求得能够直接求得海浪方向谱。其方法相较于参数法最大的优点即为计算量远远小于参数法的计算量。