一种基于混合Copula函数的多风场出力预测方法与流程

本发明涉及一种基于混合copula函数的多风场出力预测方法，属于电气工程技术领域。

背景技术：

风能作为目前使用最广泛的可持续新资源之一，其资源开发具有集中式、连片式的特点。由于地域和气候的相似性，一定区域内的风电场风电出力之间具有很强的相关性。由于这种相关性会影响电力系统安全稳定运行而受到越来越多的研究者的重视。

在实际系统运行过程中，通过分析风电场出力的随机特性，构建典型风电出力场景，针对典型场景制定应对风功率随机变化的措施，是求解含风电电力系统优化运行问题的一种重要手段。

传统的风电出力预测模型中假定并网风电的预测误差服从正态分布，虽然符合统计学规律，但没有考虑并网之前多风场之间的相关性。当并网风电是从两个或多个区域风电场合并得到时，各风场出力是具有时空上的相关性的。相同区域内的风电场风出力之间存在较强的相关性，而传统的风场出力预测方法并没有考虑相关性。

技术实现要素：

针对现有技术的不足，本发明提出了一种基于混合copula函数的多风场出力预测方法，其能够有效解决地域上具有相关性的多风场并网出力预测问题。

本发明解决其技术问题采取的技术方案是：一种基于混合copula函数的多风场出力预测方法，其特征是，包括以下步骤：

1)构建混合copula函数模型；

2)模型选择和参数估计；

3)具有相关性的多风场出力预测。

进一步地，在步骤1)中，所述的混合copula函数模型为：

其中，ck(u1,u2；θk)为已知的copula函数，u1,u2为随机变量，θk为相依参数，λk为权重系数，满足0≤λk≤1，k＝4，已知的copula函数包括gauss-copula函数、frank-copula函数、gumbel-copula函数和clayton-copula函数。

进一步地，在步骤2)中，模型选择和参数估计的过程包括以下步骤：首先构建惩罚似然函数，其次对边缘分布的估计，然后对混合copula函数中的权重参数和相依参数进行估计，最后采用交叉验证法来对γ和α进行估计。

进一步地，所述构建惩罚似然函数的过程为：

假设二维随机变量(x，y)的边缘分布为x～fx(x；α)，y～gy(y；β)，且其混合copula函数为则(x，y)的联合分布为：

其中，

则(x，y)的密度函数为：

其中，

在得到参数φ的估计值之前，首先求出(x，y)的极大似然函数：

其中，fx(xi；α)和gy(yi；β)为边缘密度函数；(xn，yn)为来自(x，y)的样本，n＝1,2,…,n，n为样本容量；

构建的惩罚似然函数为：

其中，{pγt}是光滑参数，控制模型的复杂性。

进一步地，所述对边缘分布的估计的过程就是对采用非参数核密度估计，得到密度函数的估计值和从而得到边缘分布函数的估计值和

所述对混合copula函数中的权重参数和相依参数进行估计的过程为：把边缘分布函数的估计值代入二元gauss-copula的概率密度函数，得到：

并采用em算法来估计(λk，θk)。

进一步地，所述非参数核密度估计为：

设k¹(·)为r¹上的一个给定概率密度函数。hm>0是一个与m有关的常数，满足n→∞，hm→0，则称

为f(x)的一个核密度估计，其中，k¹(·)为核函数，hm称为窗宽或光滑参数。

进一步地，所述采用em算法来估计(λk，θk)的过程为：

e步，求期望：给定观测数据x和当前系数估计值，计算完全数据的对数似然函数lnp(x,y|θ)关于未知数据y的条件期望分布，即：

其中，θ^i-1为已知的当前系数的估计值；

m步，求极大值：将q(θ|θ^i-1,y)关于θ极大化，即找一个θⁱ点，使得

从而形成了一次迭代θⁱ→θ^i-1；

最后将上述e步和m步进行迭代直至||θⁱ-θ^i-1||或||q(θⁱ|θ^i-1,y)-q(θ^i-1|θ^i-1,y)||充分小为止。

进一步地，在采用em算法来估计(λk，θk)的过程需要用到而该式没有显式表达形式，采用拟牛顿法中的bfgs算法来得到θ的更新方程；

设采用拟牛顿法中的bfgs算法来得到θ的更新方程的具体过程包括以下步骤：

step1：给定初始点θ¹，允许误差ε>0；

step2：设矩阵h1＝ik(k阶单位矩阵)，计算出在θ¹处的梯度置i＝1；

step3：令迭代方向dⁱ＝-higi；

step4：从θⁱ出发，沿着方向dⁱ进行线性搜索，使它满足令θⁱ⁺¹＝θⁱ+αidⁱ；

step5：检验是否满足收敛准则，若则停止迭代，得到近似解θ＝θⁱ⁺¹，否则，进行step6；

step6：若i＝k，则令θ¹＝θⁱ⁺¹，返回进行step2，否则进行step7；

step7：令pⁱ＝θⁱ⁺¹-θⁱ，qⁱ＝gi+1-gi，同时令

置i＝i+1，返回step3。

进一步地，所述采用交叉验证法来对γ和α进行估计的过程为：

设d为完整的数据集，把完整的数据分成m分，di，i＝1,2,…,m，把di作为检验集，d-di作为交叉验证训练集；对任意给定罚函数的参数(γ，α)，先首先采用d-di的数据，通过上面的em算法分别得到权重系数λ和相依系数θ的估计值然后计算选择使得下式最大的光滑参数：最后得出(γ，α)的估计值

进一步地，在步骤3)中，具有相关性的多风场出力预测的具体过程为：

设两相邻风电场一天t＝96个时段的风电出力为随机变量，即t组相关的二元随机变量(u11，u21),(u12，u22)，…，(u1t，u2t)，通过对其进行分析确定混合copula函数的各项参数；

所述确定混合copula函数的各项参数的过程包括以下步骤：首先，对混合copula函数的拟合效果进行检验；然后，用mc法产生服从各copula函数的随机变量的概率；最后，对以上随机变量进行累积分布逆变换，即非参数核密度估计，从而生成服从风电场出力联合分布的预测结果。

本发明的有益效果如下：

本发明通过结合4种copula函数构建混合copula函数模型，提出了一种基于混合copula函数的多风场出力预测方法，它对相同区域内的风电场风出力之间存在较强的相关性进行分析，解决了地域上具有相关性的多风场并网出力预测问题。

本发明结合4种copula函数构建混合copula函数模型，其拟合精度优于单一copula函数，对相同区域内的风电场风出力之间存在较强的相关性进行分析，在应用于调度时有利于风电的消纳。当风电采用多风场并网的方式时，采用本发明提出的多风场出力预测方法不仅优于假设预测场景的误差分布呈正态分布的出力预测方法，而且在并网调度时更有利于系统对风电的消纳。

附图说明

图1为本发明的方法流程图；

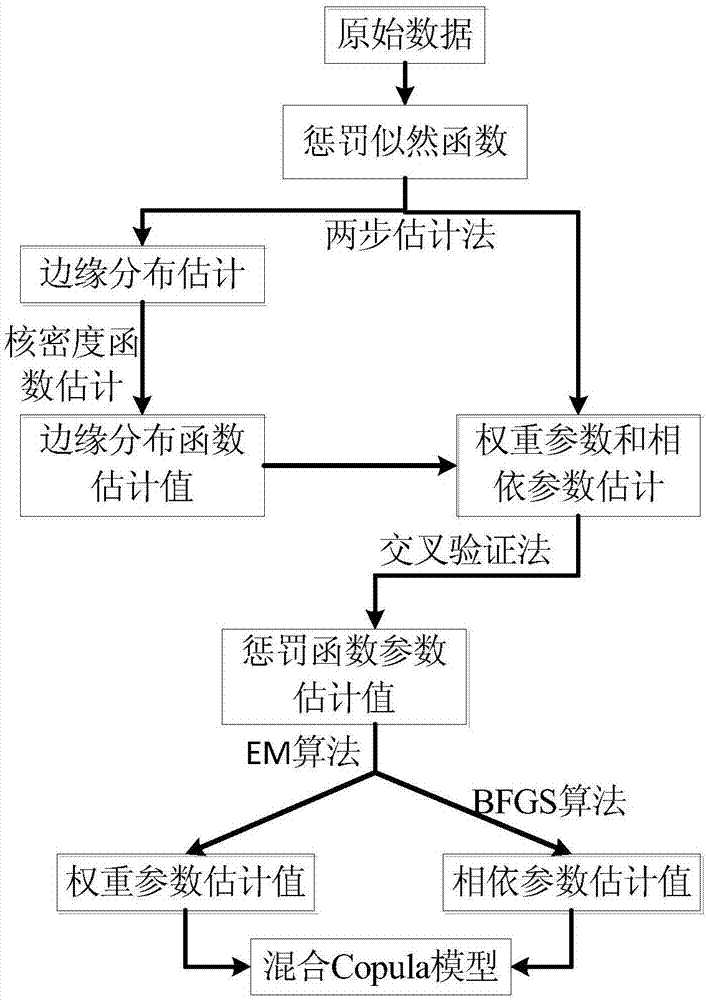
图2为本发明的模型选择和参数估计流程图；

图3为本发明算例中第一组预测场景风电出力的数据曲线图；

图4为本发明算例中第二组预测场景风电出力的数据曲线图。

具体实施方式

为能清楚说明本方案的技术特点，下面通过具体实施方式，并结合其附图，对本发明进行详细阐述。下文的公开提供了许多不同的实施例或例子用来实现本发明的不同结构。为了简化本发明的公开，下文中对特定例子的部件和设置进行描述。此外，本发明可以在不同例子中重复参考数字和/或字母。这种重复是为了简化和清楚的目的，其本身不指示所讨论各种实施例和/或设置之间的关系。应当注意，在附图中所图示的部件不一定按比例绘制。本发明省略了对公知组件和处理技术及工艺的描述以避免不必要地限制本发明。

如图1所示，本发明的一种基于混合copula函数的多风场出力预测方法，它包括以下步骤：

1)构建混合copula函数模型；

2)模型选择和参数估计；

3)具有相关性的多风场出力预测。

在步骤1)中，混合copula函数模型描述如下：

不同类型的copula函数描述变量相关性的侧重点不同。gauss-copula函数和frank-copula函数适合描述数据间的对称相关性；gumbel-copula函数刻画了非对称的上尾相关性，clayton-copula函数刻画了非对称的下尾相关性。这样如果在实际应用中只用某一种copula函数来拟合数据，可能会出现失真的情况。由于不同的copula函数对相关性描述的侧重点不同，因此考虑把这几种copula函数混合在一起，这样混合copula函数就能更好地描述数据间的相关性，更好地融合数据。二元混合copula的函数模型如下：

其中，为已知的copula函数，θk为相依参数，λk为权重系数，满足0≤λk≤1，且混合copula函数仍是copula函数。

在步骤2)中，如图2所示，混合copula函数模型的模型选择和参数估计流程如下：

这一步要解决的是混合copula函数的模型选择和参数估计问题。利用惩罚似然函数对混合copula函数进行模型选择和参数估计，选择和估计的步骤分为两步：首先就是对边缘分布的估计，本文引入非参数中核密度估计对边缘分布进行参数估计；接着就是对混合copula函数中的权重参数和相依参数进行估计。由于惩罚似然函数中涉及到多重求和的函数形式，对其最大化比较困难，故采用em(expectation&maximization)算法^[101]进行处理。其中，对em算法中m步，利用最优化方法中的bfgs^[102]算法进行解决，从而完成对混合copula函数的模型选择和参数估计。

1、惩罚似然函数

假设二维随机变量(x，y)，设其边缘分布为x～fx(x；α)，y～gy(y；β)，且设其混合copula函数为则的联合分布为(x，y)为：

其中，则可知(x，y)的密度函数为：

其中，

想要得到参数φ的估计值，首先求出(x，y)的极大似然函数，即：

其中，fx(xi；α)和gy(yi；β)为边缘密度函数；(xn，yn)，n＝1,2,…,n。为来自(x，y)的样本，n为样本容量。

如果只是对求得的极大似然函数进行估计的话，可能会把不显著的copula函数(相关性描述不显著)选进去，这样会造成模型失真。这其实是一个模型选择的问题，因此，通过引入惩罚函数来对权重参数进行惩罚选择。这样可以利用惩罚函数把一些不显著的copula函数剔除，从而可以使模型更好地拟合数据。为此构建惩罚似然函数：

其中，{pγt}是光滑参数，控制模型的复杂性。本节对各个权重的惩罚函数均采用scad惩罚(smoothlyclippedabsolutedeviationpenalty)函数，该函数满足一个好的惩罚函数需要具有的无偏性、稀疏性和连续性，三个性质。

2、两步估计惩罚函数

对二元gauss-copula的概率密度函数参数的估计，可以分成两步。首先就是对边缘分布的参数进行估计，然后对混合copula函数的权重参数及相依参数进行估计。具体步骤如下：

第一步：

对采用非参数核密度估计，得到密度函数的估计值从而得到边缘分布函数的估计值

第二步：

把边缘分布函数的估计值代入二元gauss-copula的概率密度函数，得到：

对阿基米德copula的概率密度函数采用em法来估计(λk，θk)。

(1)边缘分布的核密度估计

从对边缘分布的估计，有学者采用经验分布对边缘分布进行估计，然而经验分布一般不连续或光滑性不够，用来表述边缘分布会产生较大的误差。还有的学者就直接假设其分布，然后去验证。然而采用这种方法会使得验证步骤变得繁琐，所以具有一定局限性。对此，本发明采用非参数的方法，即，核密度估计来对边缘分布进行估计，从而实现用数据来拟合边缘分布，使模型更加真实。

非参数核密度估计是由rosenblatt和parzen提出的，下面给出核密度估计的定义：

设k¹(·)为r¹上的一个给定概率密度函数。hm>0是一个与m有关的常数，满足n→∞，hm→0，则称

为f(x)的一个核密度估计。其中，k¹(·)为核函数，hm称为窗宽或光滑参数。本发明采用高斯核，窗宽采用经验法则^[104]：具体为ksdensity/matlab函数。

(2)em算法

这样在边缘分布利用非参数核密度估计估计出边缘分布函数后，接下来要估计的是混合copula的权重系数和相依系数。由于混合copula的极大似然函数很复杂，无法用求偏导的方法进行解决，因此本发明采用em算法来解决此问题。

em算法是一种迭代算法，由dempster.laird和rubin于1977年提出的。它可广泛地应用于不完全数据，如缺损数据、截尾数据、成群数据、带有讨厌参数的数据。em算法主要有两步：第一步，求期望，即e步；第二步，求极大值，即m步。具体地讲：

e步：给定观测数据x和当前系数估计值，计算完全数据的对数似然函数lnp(x,y|θ)关于未知数据y的条件期望分布，即：

其中，θ^i-1为已知的当前系数的估计值。

m步：将q(θ|θ^i-1,y)关于θ极大化，即找一个θⁱ点，使得

从而形成了一次迭代θⁱ→θ^i-1。将上述e步和m步进行迭代直至||θⁱ-θ^i-1||或||q(θⁱ|θ^i-1,y)-q(θ^i-1|θ^i-1,y)||充分小为止。

在用em法解决二元copula概率密度函数参数估计的过程中需要用到而该式没有显式表达形式，所以采用拟牛顿法中的bfgs算法来解决。

(3)bfgs算法

bfgs算法是拟牛顿法中的一种应用较为广泛的解决非线性优化问题的算法。其主要是在牛顿法的基础上进行改进。由于牛顿法中需要计算二阶偏导数而且要求目标函数的hesse矩阵为对称正定矩阵，这些条件较为苛刻。因此对牛顿法进行改进，学者们提出拟牛顿法。拟牛顿法主要是根据taylor公式的近似展开式得到的拟牛顿方程来构造矩阵，以此来近似hesse矩阵或其逆矩阵，并求得迭代方向。由于构造矩阵的方法不同，从而出现不同的拟牛顿法，本发明采用由broyden，foldfarb和shanno于1970年提出的bfgs算法。

设下面具体给出bfgs算法的计算步骤：

step1：给定初始点θ¹，允许误差ε>0。

step2：设矩阵h1＝ik(k阶单位矩阵)，计算出在θ¹处的梯度置i＝1。

step3：令迭代方向dⁱ＝-higi。

step4：从θⁱ出发，沿着方向dⁱ进行线性搜索，使它满足令θⁱ⁺¹＝θⁱ+αidⁱ(更新方程)。

step5：检验是否满足收敛准则，若则停止迭代，得到近似解θ＝θⁱ⁺¹，否则，进行step6。

step6：若i＝k，则令θ¹＝θⁱ⁺¹，返回进行step2，否则进行step7。

step7：令pⁱ＝θⁱ⁺¹-θⁱ，qⁱ＝gi+1-gi，同时令

置i＝i+1，返回step3。这样通过bfgs算法可以得到θ的更新方程。

通过上面em算法和bfgs算法的结合可以得到权重系数λ＝(λ1,...,λk)^t和相依系数θ＝(θ1,...,θk)^t的估计值。在上面的估计过程中要用到scad惩罚函数中的光滑参数γ和α。下面采用交叉验证法来对γ和α进行估计。

(4)交叉验证法

交叉验证法一般是采用平均平方误差准则，其基本原理就是把数据分为两部分：第一部分作为检测集用来预测(或检验)，第二部分作为训练集用来进行估计。具体如下：

设d为完整的数据集，把完整的数据分成m分，di(i＝1,2,…,m)。这里把di作为检验集，d-di作为交叉验证训练集。对任意给定罚函数的参数(γ，α)，先首先采用d-di的数据，通过上面的em算法分别得到权重系数λ和相依系数θ的估计值然后计算选择使得下式最大的光滑参数：这样得出(γ，α)的估计值后，继续利用前面的em算法对完整数据集d进行参数估计得出权重系数及相依系数的估计值。

在步骤3)中，具有相关性的多风场出力预测表述如下：

设两相邻风电场一天t＝96个时段的风电出力为随机变量，即t组相关的二元随机变量(u11，u21),(u12，u22)，…，(u1t，u2t)。对其进行分析，确定混合copula函数的各项参数。首先，对混合copula函数的拟合效果进行检验。然后，用mc法产生服从各copula函数的随机变量的概率，可调用matlab中的copularnd函数生成。最后，对以上随机变量进行累积分布逆变换，即非参数核密度估计，可调用matlab中的ksdensity函数生成。从而生成服从风电场出力联合分布的预测结果。

下面通过算例来验证本发明对两个风场出力进行预测的情况。

(1)第一组风电数据，两风电场大约相距80公里。风电场一最大出力为422mw，风电场二最大出力为472mw，并网最大出力为860mw。图3为第一组预测场景风电出力曲线图，表1为第一组数据下不同copula函数的对比。

表1第一组数据下不同copula函数的对比

由表1可以看出，第一组数据中两风场出力的相关性最符合clayton-copula分布；混合copula函数权重系数λ3＝1，其余为零。拟合效果相同，选择完全服从clayton-copula分布。

(2)第二组风电数据，两风电场大约相距40公里。风电场一最大出力为615mw，风电场二最大出力为538mw，并网最大出力为1050mw。图4为第二组预测场景风电出力曲线图，表2为第二组数据下不同copula函数的对比。

表2第二组数据下不同copula函数的对比

由表2可以看出，混合copula函数权重系数λ3＝0.5351，λ4＝0.4649，其余为零。对第二组数据的拟合效果优于用几种copula单独拟合得到的结果。综上，混合copula得到的拟合数据总是优于(至少不弱于)几种copula单独拟合得到的结果。

以上所述只是本发明的优选实施方式，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也被视为本发明的保护范围。