基于有限状态的旋翼系统诱导流场的轴向诱导速度计算方法与流程

本发明涉及旋翼系统诱导流场的轴向诱导速度计算方法。

背景技术：

伴随着直升机，大型风机发电设备的不断发展，为满足相应的系统的设计指标和要求，深入了解系统动态特性，准确的模型已经显得越来越重要。而在这类系统中，无疑旋翼系统的模型和动态将起到重要的影响，而准确计算旋翼的动态特性的关键之一是精确表达旋翼桨盘及其周围的空气诱导速度，它与旋翼存在着作用与反作用的关系。当旋翼发生扰动时，旋翼气动载荷的变化必然引起诱导速度的变化，而这一变化又会反过来影响旋翼的气动载荷，进而影响旋翼的运动特性。旋翼系统坐标系的建立如图1所示。

准确的计算空气诱导速度场是旋翼系统准确建模的关键问题，国内外很多旋翼系统的建模过程中，采用动量定理或者pitt-peters等较低阶次的动态入流模型，导致建模误差较大，无法准确地反映旋翼系统相关特性。虽然也有高阶次的动态入流模型提出和应用，如peters-he模型和peters-morillo模型，但这两个模型均有其固有的不足和缺陷，制约了他们的应用。而运用大型流体计算软件计算诱导流场，往往边界条件设置复杂，计算量大，耗时耗力且无法保证实时性。与此同时，现代对直升机，大型风力发电机的要求越来越高，疲劳特性和机动特性等应该在设计阶段就得到预先分析、计算和检验，必然需要较高精度的模型予以验证；以上问题导致现有的计算方法难以同时兼顾快速计算和快速收敛的要求。

技术实现要素：

本发明的目的是为了解决现有计算方法难以同时兼顾快速计算和快速收敛的要求的问题，而提出基于有限状态的旋翼系统诱导流场的轴向诱导速度计算方法。

基于有限状态的旋翼系统诱导流场的轴向诱导速度计算方法具体过程为:

步骤一、获取旋翼平面上方空间内测试点集在椭圆坐标系ν,η,下的坐标；

步骤二、设定最大谐波参数n(设定范围一般可选为8-15)，根据最大谐波参数求解相应矩阵参数，并根据正弦分量的动态压力系数余弦分量的动态压力系数及相应矩阵参数，求解

相应矩阵参数为[m^c]、[m^s]、[d^c]、[d^s]、[l^c]、[l^s]；

其中[m^c]、[m^s]代表余弦和正弦分量的质量矩阵，[d^c]、[d^s]代表余弦和正弦分量的阻尼矩阵，[l^c]为余弦分量的关联系数矩阵、[l^s]为正弦分量的关联系数矩阵，为peters-morillo模型展开系数；

步骤三、根据(包含奇偶数量)求解(只包含奇数量)；

其中为混合模型中分别对应余弦和正弦奇数量的系数；

步骤四、根据和步骤一获取的测试点集在椭圆坐标系ν,η,下的坐标构建混合模型，基于混合模型求解旋翼平面上方测试点处诱导流场的轴向诱导速度

步骤五、根据混合模型计算得到的旋翼平面上方测试点处的轴向诱导速度和peters-morillo模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度建立重构模型，根据重构模型计算旋翼平面上方测试点处诱导流场的轴向诱导速度vz；

步骤六、利用基因算法、蚂蚁算法或粒子算法对重构模型中的系数进行优化，使重构模型误差达到最小，最终求出优化后重构模型，根据优化后重构模型计算旋翼平面上方测试点处诱导流场的轴向诱导速度v′z。

本发明的有益效果为：

本发明方法通过建立旋翼平面上方测试点集在椭圆坐标系ν,η,下的坐标，整合了现有的peters-he模型与peters-morillo模型，求解相应矩阵参数，构建混合模型，基于混合模型求解旋翼平面上方测试点处诱导流场的轴向诱导速度并根据旋翼平面上方测试点处诱导流场的轴向诱导速度和peters-morillo模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度建立重构模型，根据重构模型计算旋翼平面上方测试点处诱导流场的轴向诱导速度vz，对重构模型中的a、c进行优化，使误差e达到最小，并求出优化后重构模型，根据优化后重构模型最终得到旋翼平面上方测试点处诱导流场的轴向诱导速度v′z，完成本发明基于有限状态的旋翼系统诱导流场的轴向诱导速度计算方法，达到了同时兼顾快速计算和快速收敛的要求。

结合实施例一选取a＝19.8,c＝0.3，作为一组假定优化后的参数，比较改进后模型的优越性。其中图4-图9为旋翼系统z＝0平面上，不同角度下，在静态压力(ω＝0)和动态压力(ω＝4)下的轴向诱导速度对比图。可以看出在-1＜x＜1区间上，重构模型比peters-morillo模型接近准确理论解，尤其在大角度时(χ＝89°)，改进效果更明显。在边沿处，可以有效计算轴向诱导速度。在-1＜x＜1区间外与peters-morillo模型收敛速度基本一致。图10-图13为旋翼系统z＝-0.5平面上不同角度下，在静态压力(ω＝0)和动态压力(ω＝4)下的轴向诱导速度对比图。可以看出在旋翼平面上方，重构模型和peters-morillo模型具有相似的收敛速度和准确性。以上结果也充分说明，本发明的计算方法在大角度、旋翼边缘有更好的收敛特性。

附图说明

图1为建立的旋翼系统坐标系示意图；

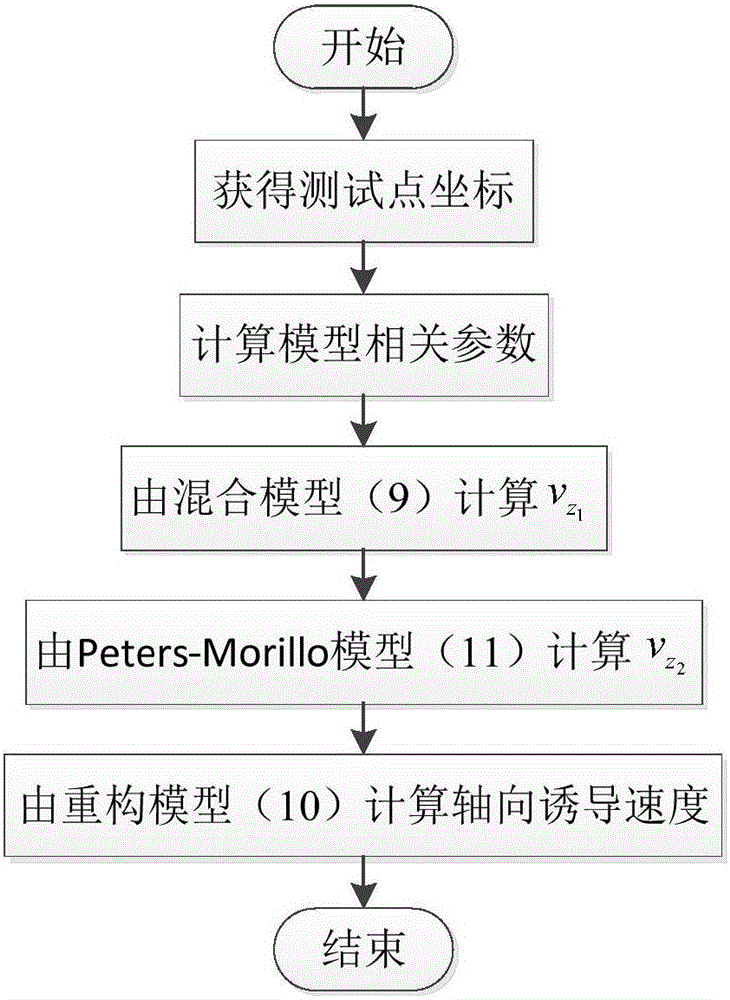
图2为重构模型计算算法流程图；

图3为优化过程流程图；

图4为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝0及时轴向诱导速度对比结果图(χ＝0°，静态压力ω＝0)；x,y,z为笛卡尔坐标系下的坐标，为对应模态的动态压力系数，ω为动态压力的频率，peter-morrilo模型为(11)式，χ指尾流倾角；

图5为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝0及时轴向诱导速度对比结果图(χ＝45°，静态压力ω＝0)；

图6为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝0及时轴向诱导速度对比结果图(χ＝89°，静态压力ω＝0)；

图7为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝0及时轴向诱导速度对比结果图(χ＝0°，动态压力ω＝4)；

图8为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝0及时轴向诱导速度对比结果图(χ＝45°，动态压力ω＝4)；

图9为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝0及时轴向诱导速度对比结果图(χ＝89°，动态压力ω＝4)；

图10为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝-0.5及时轴向诱导速度对比结果图(χ＝0°，静态压力ω＝0)；

图11为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝-0.5及时轴向诱导速度对比结果图(χ＝89°，静态压力ω＝0)；

图12为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝-0.5及时轴向诱导速度对比结果图(χ＝0°，动态压力ω＝4)；

图13为peter-morrilo模型方法、本发明重构模型方法、准确理论解方法在y＝0,z＝-0.5及时轴向诱导速度对比结果图(χ＝89°，动态压力ω＝4)。

具体实施方式

具体实施方式一：本实施方式为基于有限状态的旋翼系统诱导流场的轴向诱导速度计算方法具体过程为：

步骤一、获取旋翼平面上方空间内(是旋翼平面上方的半球形空间区域内，半径可以无穷大，旋翼平面把空间分为上半球和下半球空间)测试点集在椭圆坐标系ν,η,下的坐标；

步骤二、根据精度要求和实际情况，设定最大谐波参数n(设定范围一般可选为8-15)，根据最大谐波参数求解相应矩阵参数，并根据正弦分量的动态压力系数余弦分量的动态压力系数及相应矩阵参数，结合方程(4)，(5)求解

相应矩阵参数为[m^c]、[m^s]、[d^c]、[d^s]、[l^c]、[l^s]；

其中[m^c]、[m^s]代表余弦和正弦分量的质量矩阵，[d^c]、[d^s]代表余弦和正弦分量的阻尼矩阵，[l^c]为余弦分量的关联系数矩阵、[l^s]为正弦分量的关联系数矩阵，为peters-morillo模型展开系数；

步骤三、根据(包含奇偶数量)求解(只包含奇数量)；

其中为混合模型中分别对应余弦和正弦奇数量的系数；

步骤四、根据和步骤一获取的测试点集在椭圆坐标系ν,η,下的坐标构建混合模型，基于混合模型求解旋翼平面上方测试点处诱导流场的轴向诱导速度

步骤五、根据混合模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度和peters-morillo模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度建立重构模型，根据重构模型计算旋翼平面上方测试点处诱导流场的轴向诱导速度vz；如图2所示；

步骤六、利用基因算法、蚂蚁算法或粒子算法对重构模型中的系数进行优化，使重构模型误差达到最小，最终求出优化后重构模型，根据优化后重构模型计算旋翼平面上方测试点处诱导流场的轴向诱导速度v′z。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤一中获取旋翼平面上方测试点集在椭圆坐标系ν,η,下的坐标；具体过程为：

以旋翼中心为原点，建立如图1所示直角坐标系，χ代表尾流倾角，利用如下公式，将笛卡尔坐标系下的坐标转换为椭圆坐标系下的坐标

其中r′²＝x²+y²+z²，r′为测试点与原点间的距离；x,y,z代表测试点集在笛卡尔坐标系下的坐标，ν,η,代表测试点集在椭圆坐标系下的坐标；其中η＝0代表了旋翼所在的圆形区域。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤二中根据精度要求和实际情况，设定最大谐波参数n(设定范围为8-15)，根据最大谐波参数求解中相应矩阵参数，并根据正弦分量的动态压力系数余弦分量的动态压力系数及相应矩阵参数，结合方程(4)，(5)求解

相应矩阵参数为[m^c]、[m^s]、[d^c]、[d^s]、[l^c]、[l^s]；

其中[m^c]、[m^s]代表余弦和正弦分量的质量矩阵，[d^c]、[d^s]代表余弦和正弦分量的阻尼矩阵，[l^c]为余弦分量的关联系数矩阵、[l^s]为正弦分量的关联系数矩阵，为peters-morillo模型展开系数；具体过程为：

在此，我们通过如下公式，分别计算peters-morillo模型的余弦和正弦分量：

其中代表系数的一阶导数，[]^-1表示对关联系数矩阵求逆运算；且[m^c]、[m^s]、[d^c]、[d^s]、[l^c]、[l^s]矩阵的构造均遵从如下的关系：

其中m、n、j、r为矩阵元素所在位置的索引信息，且满足r≤j≤n，m≤n≤n，odd代表加和为奇数，even代表加和为偶数；m、n、j、r取值为正整数；

[m^c]、[m^s]、[d^c]、[d^s]、[l^c]、[l^s]矩阵中各元素计算公式如下：

[m^c]和[m^s]矩阵中各元素的计算公式为([m^c]和[m^s]矩阵元素的计算是相同的)：

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

r＝m；j+r＝odd；n+m＝even；

为中间变量；

(a)！！代表数a的双阶乘，有如下定义

(a)！！＝a(a-2)(a-4)…2,a＝even

(a)！！＝a(a-2)(a-4)…1,a＝odd

0！！＝1；(-1)！！＝1；(-2)！！＝∞；(-3)！！＝-1；

(a)！！表示(n+m-1)！！、(n-m-1)！！、(n+m)！！、(n-m)！！、(j+m-1)！！、(j-m-1)！！、(j+m)！！、(j-m)！！；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)，

当r＝m；j＝n±1；j+r＝odd；n+m＝even；

当r＝m；j＝n±1；j+r＝even；n+m＝odd；

为中间变量；

(a)！！代表数a的双阶乘，有如下定义

(a)！！＝a(a-2)(a-4)…2,a＝even

(a)！！＝a(a-2)(a-4)…1,a＝odd

0！！＝1；(-1)！！＝1；(-2)！！＝∞；(-3)！！＝-1；

(a)！！表示(j+r-1)！！、(j-r-1)！！、(j+r)！！、(j-r)！！；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)，

当r＝m；j+r＝even；n+m＝even；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r≠m；

其中[m^c]和[m^s]矩阵的差别在于[m^s]矩阵中不含有r＝0的所有行和列。

[d^c]和[d^s]矩阵中各元素的计算公式为([d^c]和[d^s]矩阵元素的计算是相同的)：

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r＝m；j+r＝odd；n+m＝odd；

当r＝m；j+r＝even；n+m＝even；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r＝m；j+r＝odd；n+m＝even；

当r＝m；j+r＝even；n+m＝odd；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r≠m；

其中为中间变量，

其中[d^c]和[d^s]矩阵的差别在于[d^s]矩阵中不含有r＝0的所有行和列；

[l^c]矩阵和[l^s]矩阵中各元素的计算公式为：

且

式中x^m、x^|m-r|、x^|m+r|、为中间变量；

其中min(r,m)代表比较r、m，取两者中较小的整数；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r+m＝odd；j+r＝odd；n+m＝odd；

当r+m＝odd；j+r＝even；n+m＝even；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r+m＝even；j+r＝odd；n+m＝odd；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r+m＝even；j+r＝even；n+m＝even；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r+m＝odd；j+r＝odd；n+m＝even；

当r+m＝odd；j+r＝even；n+m＝odd；

(每个表达式下面的m、n、j、r的约束条件不同，决定了元素的不同位置)

当r+m＝even；j+r＝odd；n+m＝even；

当r+m＝even；j+r＝even；n+m＝odd；

其中为中间变量。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一或二不同的是：所述最大谐波参数n取值范围一般为8-15。

其它步骤及参数与具体实施方式一或二相同。

具体实施方式四：本实施方式与具体实施方式一至三之一不同的是：所述步骤三中根据(包含奇偶数量)求解(只包含奇数量)；具体过程为：

在中取奇数量的peters-morillo模型展开系数和将转换为此处将由下式计算获得

其中，f≤n，为混合模型中的奇数项系数，为由peters-morillo模型展开系数中元素索引的奇数项组成；

其中中的元素由以下公式计算获得

其它步骤及参数与具体实施方式一至三之一相同。

具体实施方式五：本实施方式与具体实施方式一至四之一不同的是：所述步骤四中根据和步骤一获取的旋翼平面上方测试点集在椭圆坐标系ν,η,下的坐标构建混合模型，基于混合模型求解旋翼平面上方测试点处诱导流场的轴向诱导速度具体过程为：

利用如公式(9)的混合模型计算旋翼平面上方测试点处诱导流场的轴向速度：

其中表示基于混合模型计算得到的旋翼平面上方测试点处诱导流场的轴向速度，表示第一类归一化勒让德函数，表示第二类归一化勒让德函数，i为复数的虚部；

该模型混合了peter-he模型的基底，保留了该模型在大角度入流时更为准确的优点，同时克服了其在旋翼平面边缘(即桨叶外缘)无法有效计算的问题。混合模型(9)更好的解决了大角度时，模型在旋翼平面内的快速收敛问题。但由于该模型中混合了peters-he模型的基底，故该模型仅能用于准确计算旋翼所在平面内轴向诱导速度的缺陷也将影响到新模型。因此在非旋翼平面内，其收敛是病态的，不能快速有效的计算旋翼上方的诱导流场。下面将利用重构模型，完成旋翼平面上方测试点处诱导流场的计算。

其它步骤及参数与具体实施方式一至四之一相同。

具体实施方式六：本实施方式与具体实施方式一至五之一不同的是：所述步骤五中根据混合模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度和peters-morillo模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度建立重构模型(10)，根据重构模型(10)计算旋翼平面上方测试点处诱导流场的轴向诱导速度vz；具体过程为：

其中vz代表旋翼平面上方测试点处诱导流场的轴向诱导速度，表示由peters-morillo模型计算得到的旋翼平面上方测试点处诱导流场的轴向诱导速度，a,c为与重构模型收敛速度相关的系数；

其它步骤及参数与具体实施方式一至五之一相同。

具体实施方式七：本实施方式与具体实施方式一至六之一不同的是：所述步骤六中利用基因算法、蚂蚁算法或粒子算法对重构模型(10)中的系数(a、c)进行优化，使重构模型误差(e)达到最小，最终求出优化后重构模型(10)，根据优化后重构模型计算旋翼平面上方测试点处诱导流场的轴向诱导速度v′z；如图3所示。具体过程为：

上述模型中存在两组待定参数a,c，其决定了重构模型中和的权重，显然在旋翼平面内更为精确，而在平面外，计算结果将更依赖于为了进一步减少重构模型计算误差，可对参数a,c进行优化。首先，根据需要解决的问题和实际需求，选取兴趣区域。在区域内，随机均匀选取p个参照点，用以更全面反应区域内的特性。

利用卷积公式计算旋翼平面上方测试点中参照点(优化的时候选取几个参照点就行)处在给定压力系数时的轴向诱导速度的准确理论值作为与重构模型计算轴向诱导速度的参照；

利用重构模型(10)计算旋翼平面上方测试点中参照点处(优化的时候选取几个参照点就行)诱导流场的轴向诱导速度，并利用如下公式计算重构模型误差：

其中||e||²代表旋翼平面上方参照点的误差二范数的平方之和，为由重构模型计算得到的旋翼平面上方参照点k处的轴向诱导速度，为由卷积公式计算得到的旋翼平面上方参照点k处的轴向诱导速度的准确理论值；

利用基因算法、蚂蚁算法或粒子算法等优化算法，对下式进行参数优化

min||e||²subjecttoa＞0,0＜c≤1，(13)

subjecttoa＞0,0＜c≤1表示使a、c服从a＞0,0＜c≤1；

使得a,c的选取在旋翼平面上方(兴趣区内)最优，得到优化后重构模型(10)；

利用优化后重构模型(10)计算旋翼平面上方其他测试点处的诱导流场的轴向诱导速度v′z。

其它步骤及参数与具体实施方式一至六之一相同。

采用以下实施例验证本发明的有益效果：

实施例一：

本实施例基于有限状态的旋翼系统诱导流场的轴向诱导速度计算方法具体是按照以下步骤制备的：

由于选取兴趣区域，参照点，参考压力系数，容许误差等选取的不同，优化参数a,c会存在一定的差别。在此仅选取a＝19.8,c＝0.3，作为一组假定优化后的参数，比较改进后模型的优越性。这里仅考虑无量纲化后的情形，且仅针对压力系数进行说明，实际中正余弦动态压力系数可以由不同频率分量的动态压力系数的线性组合计算得到。

图4-图9为旋翼系统z＝0平面上，不同角度下，在静态压力(ω＝0)和动态压力(ω＝4)下的轴向诱导速度对比图。可以看出在-1＜x＜1区间上，重构模型比peters-morillo模型接近准确理论解，尤其在大角度时(χ＝89°)，改进效果更明显。在边沿处，可以有效计算轴向诱导速度。在区间外与peters-morillo模型收敛速度基本一致。

图10-图13为旋翼系统z＝-0.5平面上不同角度下，在静态压力(ω＝0)和动态压力(ω＝4)下的轴向诱导速度对比图。可以看出在旋翼平面上方，重构模型和peters-morillo模型具有相似的收敛速度和准确性。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。