基于轴不变量的通用3R机械臂逆解建模与解算方法与流程

本发明涉及一种多轴机器人3r机械臂逆解建模与解算方法，属于机器人技术领域。

背景技术

自主机器人研究的一个重要方面是需要解决变拓扑结构机器人的运动学建模问题。在mas中，具有动态的图结构(dynamicgraphstructure)，可以动态地建立基于运动轴的有向span树，为研究可变拓扑结构(variabletopologystructure)的机器人建模与控制奠定了基础。为此，需要提出基于轴不变量的通用机械臂逆解原理，既要建立包含坐标系、极性、结构参数、关节变量的完全参数化的正运动学模型，又要实时地计算位姿方程；一方面，可以提高机器人的自主性，另一方面，可以提高机器人位姿控制的绝对精度。

3r机械臂位置逆解是指：给定3r机械臂结构参数及期望位置，计算3个关节变量，使腕心位置与期望位置对齐。现有的基于d-h参数的3r机械臂位置逆解方法存在如下缺点：建立d-h系及d-h参数的过程不自然，应用繁琐；需要处理由计算方法导致的奇异性问题；在应用时，易引入系统测量误差。基于d-h参数的3r机械臂逆解原理不具有普适性，难以推广来解决通用6r机械臂的逆解问题。

技术实现要素：

本发明所要解决的技术问题是提供一种基于轴不变量的通用3r机械臂逆解建模与解算方法，可提高机械臂的绝对定位精度；与d-h参数相比，求解过程具有通用性，可以获得系统全部逆解。

为解决上述技术问题，本发明采用以下技术方案：

一种基于轴不变量的通用3r机械臂逆解建模与解算方法，其特征是，

应用n个“n元n阶”多项式的dixon消元与求解原理，进行位姿逆解计算，主要包括以下步骤：

【1】根据机械臂n元3d矢量位姿方程，获得n个“n元2阶”多项式方程；

【2】应用基于轴不变量的dixon行列式计算式、分块矩阵的行列式计算式或对行列式进行行阶梯化计算式简化行列式计算；

【3】应用n个“n元n阶”多项式的dixon消元与求解原理完成位姿逆解计算，其中：根据dixon矩阵的行列式为0，得到一元高阶多项式方程，应用基于友阵的一元高阶多项式方程求解一元高阶多项式方程的解。

对于任意杆件定义与欧拉四元数同构的居-吉布斯即ju-gibbs规范四元数：

其中：为gibbs矢量；gibbs共轭四元数为：

其中：

式中，为居-吉布斯规范四元数模的平方；表达形式幂符表示的x次幂；右上角角标∧或表示分隔符；轴不变量是轴不变量的叉乘矩阵；是gibbs矢量的叉乘矩阵；若用表示属性占位，则式中的表达形式表示成员访问符。

步骤【1】中，

对于轴链有

建立规范的姿态方程为：

建立规范的定位方程：

式中，为任意杆件，表达形式表示的x次幂；右上角角标∧或表示分隔符；是轴不变量的叉乘矩阵，杆件l,为杆件k,时同理替换；1为三维单位矩阵；ⁱqn表示姿态；为沿矢量轴的线位置；为零位时由原点至原点ol的平动矢量；为投影符，为在大地坐标系的投影矢量。

步骤【2】中，基于轴不变量的dixon行列式计算式为：

根据运动链dixon行列式性质有：

并记：

式中，为旋转变换矩阵；表示用辅助变量yl的前l个依次替换原变量τl中的l个变量，记“|”为替换操作符；

式(80)将及转化为关于的多重线性型；同时，对yl及τl具有对称性；

由式(47)得3r运动学方程

由式(90)得

由(91)式得

记

则由式(51)及式得(93)

由式(92)及式(93)得

由式(95)得3r运动学多项式方程

多项式系统f3(y2|t2)，根据双线性型行列式通式

则有

其中：

中组合变量系数为独立的列向量，故选取的系数来构成方阵剩余列向量一定与的各列相关；

由式(80)及式(93)得

分别表示轴2至轴3、轴3至轴3s的零位矢量、径向矢量及轴向矢量；

得简化的3元n阶dixon行列式为

式中，为大小为s×s的dixon矩阵，其第[i][j]成员为单变量τ1的n阶多项式。

步骤【2】中，分块矩阵的行列式计算式为：

若记大小为(n+m)·(n+m)的方阵为m，大小为n·n的矩阵是方阵m的前n行及任意n列元素构成的子矩阵，大小为m·m的矩阵是方阵m后m行及剩余m列元素构成的子矩阵；由升序排列的矩阵列序号构成的序列cn及cm是序列[1:m+n]的子集，[cn,cm]∈<1:n+m>，且有cm∪cn＝[1:m+n]；则方阵m行列式与分块矩阵及的行列式关系为

步骤【2】中，对行列式进行行阶梯化计算原理：

对于s×s矩阵，其每一项是关于τ1的n阶多项式；计算该矩阵的行列式时，可通过初等行变换将原行列式变为上三角行列式，再将非零的对角线元素相乘，得到行列式的多项式表达式；该式为0，得到t1的所有解；

行阶梯化的具体方法为，先对行列式第一列的最高阶次由高到低进行排序，再进行最多(s-1)×n次初等行变换消元，得到第一列只有第一个元素不为0的行列式；再对该行列式第1行及1列的余子式进行初等行变换消元，依次迭代求解。

步骤【3】中，n个“n元n阶”多项式系统的dixon多项式构建步骤为：

引入辅助变量[y2,y3,…,yn]，且有

对于多元多重多项式用辅助变量ym的前m个依次替换原变量xn中的m个变量，记“|”为替换操作符，得到增广的多项式

得

其中：

定义可分离组合变量及如下：

由式(14)及式(15)知：替换式是关于及的双重线性型；相应地，用辅助变量替换的多项式系统记为

给定n个“n元n阶”多项式系统定义其dixon多项式为

由式(17)得

考虑式(13)及式(18)得该多项式的dixon行列式

在笛卡尔空间下，由位置矢量或转动矢量构成的行列式表示矢量张成空间的容积(volume)；在不同笛卡尔空间下具有容积的不变性。其中：

给定n个“n元n阶”多项式系统fn(yn-1|xn-1)，n≥2；存在与消去变量x2,…,xn无关的dixon矩阵sθs(x1)，其dixon多项式表示为分离变量及的双重线性型：

α[l]∈[0,n·(n-l+1)-1],l∈[2:n]；(23)

为大小为s×s的dixon矩阵，其第[i][j]成员为单变量x1的n阶多项式：

其中：

考虑式(22)，若故得

det(sθs(x1))＝0；(28)

称式(28)中“n个n元”为dixon消元的必要条件，从而获得可行解。

由式(28)、式(99)及式(100)得

式(116)是关于τ1的16阶单项式方程，应用式(5)进行二次分块的行列式计算。

本发明所达到的有益效果：

本发明的方法提出了基于轴不变量的通用3r姿态逆解方法。特征在于：

具有简洁、优雅的运动链符号系统，具有伪代码的功能，具有迭代式结构，保证系统实现的可靠性及机械化演算。

具有基于轴不变量的迭代式，保证计算的实时性；实现坐标系、极性及系统结构参量的完全参数化，基于轴不变量的可逆解运动学具有统一的表达及简洁的结构化层次模型，保证位姿分析逆解(analyticalinversesolutiontopositionandattitude)的通用性。

直接应用激光跟踪仪精密测量获得的基于固定轴不变量的结构参数，保证位姿逆解的准确性；从而，使系统的绝对定位与定姿精度接近重复精度。

由于轴不变量可以精确测量，有助于提高机械臂的绝对定位精度；由于关节变量的范围覆盖完整的一周，消除了d-h计算原理导致的奇异性；与d-h参数相比，求解过程具有通用性，可以获得系统全部逆解。

附图说明

图1自然坐标系与轴链；

图2固定轴不变量；

图3为定轴转动示意图；

图4为轴不变量的导出不变量。

具体实施方式

下面对本发明作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

定义1自然坐标轴：称与运动轴或测量轴共轴的，具有固定原点的单位参考轴为自然坐标轴，亦称为自然参考轴。

定义2自然坐标系：如图1所示，若多轴系统d处于零位，所有笛卡尔体坐标系方向一致，且体坐标系原点位于运动轴的轴线上，则该坐标系统为自然坐标系统，简称自然坐标系。

自然坐标系优点在于：(1)坐标系统易确定；(2)零位时的关节变量为零；(3)零位时的系统姿态一致；(4)不易引入测量累积误差。

由定义2可知，在系统处于零位时，所有杆件的自然坐标系与底座或世界系的方向一致。系统处于零位即时，自然坐标系绕轴矢量转动角度将转至f^[l]；在下的坐标矢量与在f^[l]下的坐标矢量恒等，即有

由上式知，或不依赖于相邻的坐标系及f^[l]；故称或为轴不变量。在不强调不变性时，可以称之为坐标轴矢量(简称轴矢量)。或表征的是体与体l共有的参考单位坐标矢量，与参考点及ol无关。体与体l即为杆件或轴。

轴不变量与坐标轴具有本质区别：

(1)坐标轴是具有零位及单位刻度的参考方向，可以描述沿该方向平动的位置，但不能完整描述绕该方向的转动角度，因为坐标轴自身不具有径向参考方向，即不存在表征转动的零位。在实际应用时，需要补充该轴的径向参考。例如：在笛卡尔系f^[l]中，绕lx转动，需以ly或lz为参考零位。坐标轴自身是1d的，3个正交的1d参考轴构成3d的笛卡尔标架。

(2)轴不变量是3d的空间单位参考轴，其自身就是一个标架。其自身具有径向参考轴，即参考零位。空间坐标轴及其自身的径向参考轴可以确定笛卡尔标架。空间坐标轴可以反映运动轴及测量轴的三个基本参考属性。

已有文献将无链指标的轴矢量记为并称之为欧拉轴(euleraxis)，相应的关节角称为欧拉角(eulerangle)。本申请之所以不再沿用欧拉轴，而称之为轴不变量，是因为轴不变量具有以下属性：

【1】给定旋转变换阵因其是实矩阵，其模是单位的，故其有一个实特征值λ1及两个互为共轭的复特征值λ2＝e^iφ及λ3＝e^-iφ；其中：i为纯虚数。因此，|λ1|·||λ2||·||λ3||＝1，得λ1＝1。轴矢量是实特征值λ1＝1对应的特征矢量，是不变量；

【2】是3d参考轴，不仅具有轴向参考方向，而且具有径向参考零位，将在3.3.1节予以阐述。

【3】在自然坐标系下：即轴不变量是非常特殊的矢量，它对时间的导数也具有不变性，且有非常优良的数学操作性能；

对轴不变量而言，其绝对导数就是其相对导数。因轴不变量是具有不变性的自然参考轴，故其绝对导数恒为零矢量。因此，轴不变量具有对时间微分的不变性。有：

【4】在自然坐标系统中，通过轴矢量及关节变量可以直接描述旋转坐标阵没有必要为除根之外的杆件建立各自的体系。同时，以唯一需要定义的根坐标系为参考，可以提高系统结构参数的测量精度；

【5】应用轴矢量的优良操作，将建立包含拓扑结构、坐标系、极性、结构参量及力学参量的完全参数化的统一的多轴系统运动学及动力学模型。

因基矢量el是与f^[l]固结的任一矢量，基矢量是与固结的任一矢量，又是f^[l]及共有的单位矢量，故是f^[l]及共有的基矢量。因此，轴不变量是f^[l]及共有的参考基。轴不变量是参数化的自然坐标基，是多轴系统的基元。固定轴不变量的平动与转动与其固结的坐标系的平动与转动等价。

在系统处于零位时，以自然坐标系为参考，测量得到坐标轴矢量在运动副运动时，轴矢量是不变量；轴矢量及关节变量唯一确定运动副的转动关系。

因此，应用自然坐标系统，当系统处于零位时，只需确定一个公共的参考系，而不必为系统中每一杆件确定各自的体坐标系，因为它们由轴不变量及自然坐标唯一确定。当进行系统分析时，除底座系外，与杆件固结的其它自然坐标系只发生在概念上，而与实际的测量无关。自然坐标系统对于多轴系统(mas)理论分析及工程作用在于：

(1)系统的结构参数测量需要以统一的参考系测量；否则，不仅工程测量过程烦琐，而且引入不同的体系会引入更大的测量误差。

(2)应用自然坐标系统，除根杆件外，其它杆件的自然坐标系统由结构参量及关节变量自然确定，有助于mas系统的运动学与动力学分析。

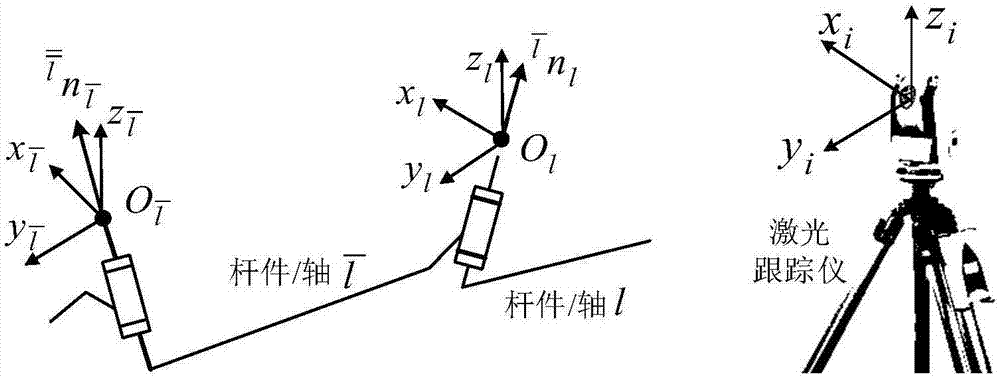
(3)在工程上，可以应用激光跟踪仪等光学测量设备，实现对固定轴不变量的精确测量。

(4)由于运动副r及p、螺旋副h、接触副o是圆柱副c的特例，可以应用圆柱副简化mas运动学及动力学分析。

定义3不变量：称不依赖于一组坐标系进行度量的量为不变量。

定义4转动坐标矢量：绕坐标轴矢量转动到角位置的坐标矢量为

定义5平动坐标矢量：沿坐标轴矢量平动到线位置的坐标矢量为

定义6自然坐标：以自然坐标轴矢量为参考方向，相对系统零位的角位置或线位置，记为ql，称为自然坐标；称与自然坐标一一映射的量为关节变量；其中：

定义7机械零位：对于运动副在初始时刻t0时，关节绝对编码器的零位不一定为零，该零位称为机械零位；

故关节的控制量为

定义8自然运动矢量：将由自然坐标轴矢量及自然坐标ql确定的矢量称为自然运动矢量。其中：

自然运动矢量实现了轴平动与转动的统一表达。将由自然坐标轴矢量及关节确定的矢量，例如称为自由运动矢量，亦称为自由螺旋。显然，轴矢量是特定的自由螺旋。

定义9关节空间：以关节自然坐标ql表示的空间称为关节空间。

定义10位形空间：称表达位置及姿态(简称位姿)的笛卡尔空间为位形空间，是双矢量空间或6d空间。

定义11自然关节空间：以自然坐标系为参考，通过关节变量表示，在系统零位时必有的关节空间，称为自然关节空间。

如图2所示，给定链节原点ol受位置矢量约束的轴矢量为固定轴矢量，记为其中：

轴矢量是关节自然坐标的自然参考轴。因是轴不变量，故称为固定轴不变量，它表征了运动副的结构关系，即确定了自然坐标轴。固定轴不变量是链节结构参数的自然描述。

定义12自然坐标轴空间：以固定轴不变量作为自然参考轴，以对应的自然坐标表示的空间称为自然坐标轴空间，简称自然轴空间。它是具有1个自由度的3d空间。

如图2所示，及不因杆件ωl的运动而改变，是不变的结构参考量。确定了轴l相对于轴的五个结构参数；与关节变量ql一起，完整地表达了杆件ωl的6d位形。给定时，杆件固结的自然坐标系可由结构参数及关节变量唯一确定。称轴不变量固定轴不变量关节变量及为自然不变量。显然，由固定轴不变量及关节变量构成的关节自然不变量与由坐标系至f^[l]确定的空间位形具有一一映射关系，即

给定多轴系统d＝{t,a,b,k,f,nt}，在系统零位时，只要建立底座系或惯性系，以及各轴上的参考点ol，其它杆件坐标系也自然确定。本质上，只需要确定底座系或惯性系。

给定一个由运动副连接的具有闭链的结构简图，可以选定回路中任一个运动副，将组成该运动副的定子与动子分割开来；从而，获得一个无回路的树型结构，称之为span树。t表示带方向的span树，以描述树链运动的拓扑关系。

i为结构参数；a为轴序列，f为杆件参考系序列，b为杆件体序列，k为运动副类型序列，nt为约束轴的序列即非树。为取轴序列的成员。转动副r，棱柱副p，螺旋副h，接触副o是圆柱副c的特例。

描述运动链的基本拓扑符号及操作是构成运动链拓扑符号系统的基础，定义如下：

【1】运动链由偏序集合(]标识。

【2】a^[l]为取轴序列a的成员；因轴名l具有唯一的编号对应于a^[l]的序号，故a^[l]计算复杂度为o(1)。

【3】为取轴l的父轴；轴的计算复杂度为o(1)。计算复杂度o()表示计算过程的操作次数，通常指浮点乘与加的次数。以浮点乘与加的次数表达计算复杂度非常烦琐，故常采用算法循环过程中的主要操作次数；比如：关节位姿、速度、加速度等操作的次数。

【4】为取轴序列的成员；计算复杂度为o(1)。

【5】^llk为取由轴l至轴k的运动链，输出表示为且基数记为|^llk|。^llk执行过程：执行若则执行否则，结束。^llk计算复杂度为o(|^llk|)。

【6】^ll为取轴l的子。该操作表示在中找到成员l的地址k；从而，获得轴l的子a^[k]。因不具有偏序结构，故^ll的计算复杂度为

【7】^ll表示获得由轴l及其子树构成的闭子树，^ll为不含l的子树；递归执行ll，计算复杂度为

【8】支路、子树及非树弧的增加与删除操作也是必要的组成部分；从而，通过动态span树及动态图描述可变拓扑结构。在支路^llk中，若则记即表示在支路中取成员m的子。

定义以下表达式或表达形式：

轴与杆件具有一一对应性；轴间的属性量及杆件间的属性量具有偏序性。

约定：表示属性占位；若属性p或p是关于位置的，则应理解为坐标系的原点至f^[l]的原点；若属性p或p是关于方向的，则应理解为坐标系至f^[l]。

及应分别理解为关于时间t的函数及且及是t0时刻的常数或常数阵列。但是正体的及应视为常数或常数阵列。

本申请中约定：在运动链符号演算系统中，具有偏序的属性变量或常量，在名称上包含表示偏序的指标；要么包含左上角及右下角指标，要么包含右上角及右下角指标；它们的方向总是由左上角指标至右下角指标，或由右上角指标至右下角指标，本申请中为叙述简便，有时省略方向的描述，即使省略，本领域技术人员通过符号表达式也可以知道，本申请中采用的各参数，对于某种属性符，它们的方向总是由偏序指标的左上角指标至右下角指标，或由右上角指标至右下角指标。例如：可简述为(表示由k至l)平动矢量；表示(由k至l的)线位置；表示(由k至l的)平动矢量；其中：r表示“平动”属性符，其余属性符对应为：属性符φ表示“转动”；属性符q表示“旋转变换矩阵”；属性符l表示“运动链”；属性符u表示“单位矢量”；属性符ω表示“角速度”；角标为i表示惯性坐标系或大地坐标系；其他角标可以为其他字母，也可以为数字。

本申请的符号规范与约定是根据运动链的偏序性、链节是运动链的基本单位这两个原则确定的，反映了运动链的本质特征。链指标表示的是连接关系，右上指标表征参考系。采用这种符号表达简洁、准确，便于交流与书面表达。同时，它们是结构化的符号系统，包含了组成各属性量的要素及关系，便于计算机处理，为计算机自动建模奠定基础。指标的含义需要通过属性符的背景即上下文进行理解；比如：若属性符是平动类型的，则左上角指标表示坐标系的原点及方向；若属性符是转动类型的，则左上角指标表示坐标系的方向。

(1)ls－杆件l中的点s；而s表示空间中的一点s。

(2)－杆件k的原点ok至杆件l的原点ol的平动矢量；

在自然坐标系f^[k]下的坐标矢量，即由k至l的坐标矢量；

(3)－原点ok至点ls的平动矢量；

在f^[k]下的坐标矢量；

(4)－原点ok至点s的平动矢量；

在f^[k]下的坐标矢量；

(5)－连接杆件及杆件l的运动副；

－运动副的轴矢量；

及分别在及f^[l]下的坐标矢量；是轴不变量，为一结构常数；

为转动矢量，转动矢量/角矢量是自由矢量，即该矢量可自由平移；

(6)－沿轴的线位置(平动位置)，

－绕轴的角位置，即关节角、关节变量，为标量；

(7)左下角指标为0时，表示机械零位；如：

－平动轴的机械零位，

－转动轴的机械零位；

(8)0－三维零矩阵；1－三维单位矩阵；

(9)约定：“\”表示续行符；表示属性占位；则

幂符表示的x次幂；右上角角标∧或表示分隔符；如：或为的x次幂。

表示的转置，表示对集合转置，不对成员执行转置；如：

为投影符，表示矢量或二阶张量对参考基的投影矢量或投影序列，即坐标矢量或坐标阵列，投影即是点积运算“·”；如：位置矢量在坐标系f^[k]中的投影矢量记为

为叉乘符；如：是轴不变量的叉乘矩阵；给定任一矢量的叉乘矩阵为叉乘矩阵是二阶张量。

叉乘符运算的优先级高于投影符的优先级。投影符的优先级高于成员访问符或成员访问符优先级高于幂符

(10)单位矢量在大地坐标系的投影矢量单位零位矢量

(11)－零位时由原点至原点ol的平动矢量，且记表示位置结构参数。

(12)ⁱql，相对绝对空间的旋转变换阵；

(13)以自然坐标轴矢量为参考方向，相对系统零位的角位置或线位置，记为ql，称为自然坐标；关节变量自然关节坐标为φl；

(14)对于一给定有序的集合r＝[1,4,3,2]^t，记r^[x]表示取集合r的第x行元素。常记[x]、[y]、[z]及[w]表示取第1、2、3及4列元素。

(15)ⁱlj表示由i到j的运动链；^llk为取由轴l至轴k的运动链；

给定运动链若n表示笛卡尔直角系，则称为笛卡尔轴链；若n表示自然参考轴，则称为自然轴链。

(16)rodrigues四元数表达形式：

欧拉四元数表达形式：

不变量的四元数(也称为轴四元数)表达形式

如位置矢量在笛卡尔三个坐标轴上的投影矢量为定义由于左上角指标指明了参考系，既间接表示了位移矢量又直接表示了位移坐标矢量，即具有矢量及坐标矢量的双重作用。

分块矩阵的高维行列式计算：

记<1:n>表示自然数[1:n]的全排列，共有n！个实例。给定属于数域的大小为n×n的矩阵m，其j行i列元素记为根据行列式定义得

其中：i[i1,…in]表示排列<i1,…in>的逆序个数。式(1)计算复杂度为：n！次n个数积及n！次加法，具有指数计算复杂度，只能适用于维度较小的行列式。对于维度较大的行列式，通常应用laplace公式进行递规运算，记为的伴随矩阵(adjugatematrix)，则有

更简单的算法通常应用高斯消去法或lu分解法，先通过初等变换将矩阵变为三角阵或三角阵的乘积，后计算行列式。上述针对数域的行列式计算方法不适用于高维度的多项式矩阵，需要引入分块矩阵的行列式计算方法。计算矢量多项式(vectorpolynomial)的行列式是一个特定的分块矩阵行列式的计算问题，它在矢量层次上表达了矢量与行列式的内在联系。而分块矩阵行列式计算则从矩阵层次上表达分块矩阵与行列式的内在规律。

若给定矢量多项式其中：及为3d坐标矢量，为多项式变量序列；若约定

则有

式(3)及式(4)可以推广至n维空间。

实施例1

给定2个2维行矢量多项式及一方面，由式(4)得

另一方面，

上面的结果验证了式(4)的正确性。

给出分块矩阵的行列式计算定理：

若记大小为(n+m)·(n+m)的方阵为m，大小为n·n的矩阵是方阵m的前n行及任意n列元素构成的子矩阵，大小为m·m的矩阵是方阵m后m行及剩余m列元素构成的子矩阵；由升序排列的矩阵列序号构成的序列cn及cm是序列[1:m+n]的子集，[cn,cm]∈<1:n+m>，且有cm∪cn＝[1:m+n]；则方阵m行列式与分块矩阵及的行列式关系为

对行列式进行行阶梯化计算原理：

对于s×s矩阵，其每一项是关于t1的n阶多项式。计算该矩阵的行列式时，可通过初等行变换将原行列式变为上三角行列式，再将非零的对角线元素相乘，得到行列式的多项式表达式。该式为0，得到t1的所有解。

行阶梯化的具体方法为，先对行列式第一列的最高阶次由高到低进行排序，再进行最多(s-1)×n次初等行变换消元，得到第一列只有第一个元素不为0的行列式。再对该行列式第1行及1列的余子式进行初等行变换消元，依次迭代求解。

实施例2

通过矩阵的初等行变换，得到的行阶梯矩阵。

步骤为：rk代表第k行。得

则得

基于“n进位字”的n阶多项式系统：

若n个“n元1阶”多项式幂积中独立变量重复出现n次，则得到n个“n元n阶”多项式系统“n元n阶多项式系统”与“n位n进位字”同构。

n个“n元n阶”多项式系统的dixon多项式：

引入辅助变量[y2,y3,…,yn]，且有

在多元多重多项式(8)中，用辅助变量ym的前m个依次替换原变量(originalvariables)xn中的m个变量，记“|”为替换操作符，得到增广的(extended)多项式

式中右上角标α、α表示幂；

由式(6)及式(12)得

其中：

定义可分离组合变量及如下：

由式(14)及式(15)可知：替换式是关于及的双重线性型。相应地，用辅助变量替换的多项式系统记为

给定n个“n元n阶”多项式系统定义其dixon多项式为

由式(17)得

式(15)中分离变量与文献不同：原变量xn-1被辅助变量yn-1替换的次序不同，dixon多项式也不同。考虑式(13)及式(18)得该多项式的dixon行列式

在笛卡尔空间下，由位置矢量或转动矢量构成的行列式表示矢量张成空间的容积(volume)；在不同笛卡尔空间下具有容积的不变性。其中：

n个“n元n阶”多项式的dixon行列式的阶次及替换变量项数分别为：

n个“n元n阶”dixon矩阵：

给定n个“n元n阶”多项式系统fn(yn-1|xn-1)，n≥2；存在与消去变量x2,…,xn无关的dixon矩阵sθs(x1)，其dixon多项式表示为分离变量及的双重线性型：

α[l]∈[0,n·(n-l+1)-1],l∈[2:n](23)

为大小为s×s的dixon矩阵，其第[i][j]成员为单变量x1的n阶多项式：

其中：

若

则有

考虑式(22)，若故得

det(sθs(x1))＝0。(28)

称式(28)中“n个n元”为dixon消元的必要条件，从而获得可行解。若sθs存在零行或零列向量，则无法建立x1的多项式方程；此时，通过除标量积之外的初等变换，将sθs变为行阶梯(rowechelon)矩阵ech(sθs)；在计算该矩阵的杻轴(pivot)的积之后得方阵即在sθs中选取s′个独立的列向量。

任一个n个“n元n阶”多项式系统的实例(简称多项式)记为其中：且有根据的多项式确定dixon矩阵、分离变量及选取及满足

确定双线性型

其中：中与对应的各列线性独立。因由式(22)及式(25)得

称其为结式或消去式。式(32)是单变量x1的多项式方程；消去了n-1个未知量；从而，可以获得单变量x1的可行解。若x1同时满足

则x1为正确解。将已解的x1代入式(34)，因式(32)成立且任意，故得

即有

若有必要条件

成立，解式(35)，得被消去变量的解；否则，需要结合式(16)得到全部解。考虑式(25)，因式(22)两边的x1阶次相等，故必有

若同时满足

则由式(35)能解得中n-1个互不相同的组合变量；从而，得到所有独立变量的解。

给定n个“n元n阶”多项式dixon矩阵计算步骤如下：

①确定系统结构。方程数及独立变量数记为n；独立变量记为xn；多项式复合变量记为替换变量记为替换变量数为n-1；大小为s·s的dixon矩阵记为其成员系数如式(24)所示，其中：s由式(32)确定；待消去变量为x1。

②由式(8)得x^α与对应关系，表达式(11)中至多有s项。

③根据式(19)及sarrus规则，计算dixon(fn(yn-1|xn-1))；根据对应的n进位字运算结果，完成多项式合并。

④dixon矩阵成员如式(32)所示，由式(32)计算dixon矩阵sθs的(n+1)·s²个系数。

⑤当满足式(37)及式(38)直接解判别准则时，由式(34)及式(35)得全部数值解。

实施例3

对多项式系统(39)进行dixon消元。

步骤为：该式是4个“4元1阶”多项式系统，满足dixon消元条件。由式(19)及式(22)，得

其中：

由式(34)及式(40)得5个解：

其中：不是该方程组的解。将其它解分别代入式(35)。当时，由式(35)得

解得：τ3＝1，τ4＝-2。将τ3及τ4代入式(39)得τ2＝1。同样，可得其他三组解。显然，因变量不满足式(26)，式(40)所示的dixon矩阵不对称。该例表明dixon行列式为零对于多重线性多项式系统是充分的。

基于轴不变量的定轴转动

如图3所示，给定轴矢量及与其固结的单位矢量在转动前，对于单位矢量对系统零位轴的投影矢量为对系统径向轴的矩矢量为径向矢量为

轴矢量相对于杆件及ωl或自然坐标系及f^[l]是固定不变的，故称该转动为定轴转动。单位矢量绕轴转动后，转动后的零位矢量对系统零位轴的投影矢量为转动后的零位矢量对系统径向轴的矩矢量为轴向分量为故得具有链指标的rodrigues矢量方程

因单位矢量是任意的且得具有链指标的rodrigues转动方程

若由式(42)，得若即坐标系与f^[l]的方向一致，由式(42)可知：反对称部分必有因此，系统零位是自然坐标系与f^[l]重合的充分必要条件，即初始时刻的自然坐标系方向一致是系统零位定义的前提条件。利用自然坐标系可以很方便地分析多轴系统运动学和动力学。

式(43)是关于和的多重线性方程，是轴不变量的二阶多项式。给定自然零位矢量作为的零位参考，则及分别表示零位矢量及径向矢量。式(43)即为对称部分表示零位轴张量，反对称部分表示径向轴张量，分别与轴向外积张量正交，从而确定三维自然轴空间；式(43)仅含一个正弦及余弦运算、6个积运算及6个和运算，计算复杂度低；同时，通过轴不变量及关节变量实现了坐标系及极性的参数化。

对于轴链有

由式(44)及式(43)得则是及的多重线性型，其中：l∈ⁱlk。式(43)可表示为

称(45)为改进的cayley变换。即有

由式(46)得规范的位置方程

“居-吉布斯”四元数的确定：

对于任意杆件l,定义与欧拉四元数同构的“居-吉布斯”(ju-gibbs)规范四元数：

其中：为gibbs矢量。gibbs共轭四元数为：

其中：

显然，为模的平方。因居-吉布斯四元数是四元数，故满足四元数乘法运算

其中：

由式(52)得

习惯上，单关节及运动链的期望姿态以规范的ju-gibbs四元数(简称规范ju-gibbs四元数，即“标部”为1的四元数)表示；但是它们积运算通常是不规范的，即其标部不为1。由式(53)可知：只有给定轴l及的规范ju-gibbs四元数，且两轴正交，才为规范四元数。

由式(53)得

由四维复数性质得

记由式(52)得

故为单位ju-gibbs四元数。

由式(48)至式(50)及式(55)得

由式(50)、式(54)及式(57)得

类dcm及性质：

对于轴链规范的姿态方程为：

由式(59)得

式中，为旋转变换矩阵；表示用辅助变量yl的前l个依次替换原变量τl中的l个变量，记“|”为替换操作符；

其中：

由式(61)可知：ⁱqn及是关于τk的n重2阶多项式。由式(60)可知：因与类似，故称之为类dcm(dcm，方向余弦矩阵)。由式(62)得

显然，类dcm可以通过ju-gibbs四元数表达。因此，式(59)姿态方程及式(47)位置方程是关于ju-gibbs四元数的表达式。

分块方阵的逆：

若给定可逆方阵k、b及c，其中b及c分别为l×l、c×c的方阵；a、d分别为l×c、c×l的矩阵，且

则有

基于轴不变量的dixon行列式计算原理：

下面基于轴不变量，提出径向不变量及运动链的dixon行列式基本性质，为基于轴不变量的机器人逆运动学分析奠定基础。

【1】轴不变量

首先，轴不变量与坐标轴具有本质区别：坐标轴是具有零位及单位刻度的参考方向，可以描述沿轴向平动的线位置，但不能完整描述绕轴向的角位置，因为坐标轴自身不具有径向参考方向，即不存在表征转动的零位。在实际应用时，需要补充坐标轴的径向参考。坐标轴自身是1d的，3个正交的坐标轴构成3d的笛卡尔标架；轴不变量是3d空间单位参考轴(简称3d参考轴)，具有径向参考零位。“3d参考轴”及其径向参考零位可以确定对应的笛卡尔系。以自然坐标系为基础的轴不变量可以准确地反映运动轴及测量轴的“共轴性”、“极性”与“零位”三个基本属性。

其次，轴不变量与欧拉轴具有本质的区别：方向余弦矩阵(dcm)是实矩阵，轴矢量是dcm的特征值1对应的特征矢量，是不变量；固定轴不变量是“3d参考轴”，不仅具有原点及轴向，也有径向参考零位；在自然坐标系下，轴不变量不依赖于相邻固结的自然坐标系，即在相邻固结的自然坐标系下具有不变的自然坐标；轴不变量具有幂零特性等优良的数学操作功能；在自然坐标系统中，通过轴不变量及关节坐标，可以唯一确定dcm及参考极性；没有必要为每一个杆件建立各自的体系，可以极大地简化建模的工作量。

同时，以唯一需要定义的笛卡尔直角坐标系为参考，测量轴不变量，可以提高结构参数的测量精度。基于轴不变量的优良操作及属性，可以建立包含拓扑结构、坐标系、极性、结构参量及动力学参量的迭代式的运动学及动力学方程。

由式(59)及式(47)可知：多轴系统的姿态及位置方程本质上是多元二阶多项式方程，其逆解本质上归结于多元二阶多项式的消元问题，包含dixon矩阵及dixon行列式计算的两个子问题。用式(47)的表达3r机械臂位置方程，是3个“3元2阶”多项式，应用dixon消元方法计算逆解，有两个替换变量，在计算8×8的dixon行列式时，最大可能的阶次为16。由式(4)可知：行列式计算是一个排列过程，面临着“组合爆炸”的难题。

所有的不在确定的多项式时间内可解的问题称为np问题。非确定性算法将问题分解为“猜测”与“验证”两个阶段：算法的“猜测”阶段具有非确定性，算法的“验证”阶段具有确定性，通过验证来确定猜测的解是否正确。假如可以在多项式时间内计算出来，就称为多项式非确定性问题。多元多项式的消元通常被认为是np问题。通常应用基进行多元多项式的消元，不得不求助于启发式的“猜测”与“验证”来解决问题。

【2】径向不变量

结构参数及是链节l的结构参量，在系统零位时，它们可以通过外部测量得到。如图4所示，零位矢量、径向矢量及轴向矢量是与转动角无关的不变量。其中，零位矢量是特定的径向矢量。

任一个矢量可以分解为零位矢量及轴向矢量，故有

其中：

考虑链节其d-h参数有

显然，是轴l及的公垂线或公共径向矢量，是轴l的轴向矢量。由式(65)可知：任一个结构参数矢量可分解为与坐标系为无关的零位不变量及轴向不变量它们的径向矢量记为结构参数矢量及轴不变量唯一确定径向坐标系，具有2个独立维度。若两个轴向不变量及共线，则记为

若两个零位不变量及与任两个径向不变量及共面，则记为

因此，称式(66)所示的轴向不变量及零位不变量是结构参数矢量对自然轴的分解。

由式(69)及式(70)可知：同一个轴的三个径向矢量的行列式为零；同一个轴的任意两个轴向矢量的行列式为零。可以用轴不变量及其导出的不变量来简化dixon行列式计算。

由轴不变量导出的零位矢量、径向矢量及轴向矢量具有以下关系：

称式(71)为零位矢量的反转公式；称式(72)为零位矢量与径向矢量的互换公式；称式(73)为径向矢量不变性公式。由式(65)、式(71)至式(73)得

由式(74)得

因是的对称部分的结构常数，故称式(74)为矢量的对称分解式。因是的反对称部分的结构常数，故称式(75)为矢量的反对称分解式。称式(76)为归零等式。

【3】运动链dixon行列式性质

定义

由式(52)得

其中：

由式(62)及式(66)得

由式(79)证得

式(80)可以将及可以转化为关于的多重线性型。同时，对yl及tl具有对称(轮换)性。由式(67)、式(74)及式(75)得

式(81)由三个导出的独立结构参量及一个运动变量tl构成。由式(81)得

由式(80)及式(83)得

由式(80)及式(84)得

基于轴不变量的cayley变换

当给定角度后，其正、余弦及其半角的正、余弦均是常数；为方便表达，记

由式(86)得

定义

故有

与径向矢量及切向矢量是线性关系，称为“rodrigues线性不变量”。通常称即为rodrigues或gibbs矢量，而将称为修改的rodrigues参数(mrps)

基于轴不变量的3r机械臂位置逆解方法

给定3r转动链及期望姿态轴不变量序列求关节变量序列这是3r姿态逆解问题。

【1】根据机械臂n元3d矢量位姿方程，获得n个“n元2阶”多项式方程。

由式(47)得3r运动学方程

由式(90)得

由式(91)得

若记

则由式(61)及式得(93)

由式(92)及式(93)得

下面，阐述3r机械臂运动学方程的dixon行列式的结构模型及特点。

由式(95)得3r运动学多项式方程

多项式系统f3(y2|t2)，根据双线性型行列式通式

则有

其中：

由式(18)、式(95)及式(96)得

由式(22)及式(101)可知式(99)成立。由式(80)及式(93)得

由式(93)、式(102)及式(103)得

其中：应用式(85)计算显然，式(104)中的y2阶次β2∈[0:3]及y3阶次β3∈[0:1]。考虑式(101)后三项：中的y2阶次β2∈[0:3]及y3阶次β3∈[0:1]；中的y2阶次β2∈[0:2]及y3阶次β3∈[0:1]；中的y2的阶次β2∈[0:3]及y3的阶次β3∈[0:1]。由上可知：式(101)中的y2阶次β2∈[0:3]及y3的阶次β3∈[0:1]。故有s＝8。

由式(93)、式(101)至式(104)可知：中组合变量系数为独立的列向量，故选取的系数来构成方阵剩余列向量一定与的各列相关。故式(100)成立。

【2】应用“基于轴不变量的dixon行列式计算”方法，“分块矩阵的高维行列式计算”方法或者“对行列式进行行阶梯化计算”方法简化行列式计算。

根据运动链dixon行列式性质，由式(80)及式(93)得

其中：分别表示轴2至轴3、轴3至轴3s的零位矢量、径向矢量及轴向矢量。

由式(105)得

由式(106)得

由式(107)得

由式(101)得

将式(108)至式(110)代入式(111)得

【3】应用n个“n元n阶”多项式的dixon消元与求解原理完成位姿逆解计算，其中：根据dixon矩阵的行列式为0，得到一元高阶多项式方程，应用基于友阵的一元高阶多项式方程求解一元高阶多项式方程的解。

一元n阶多项式p(x)＝a0+a1x+…an-1x^n-1+xⁿ具有n个解。若能找到一个矩阵a，满足|a-λl·1n|·vl＝0，其中：l∈[1:n]，λl为该矩阵的特征值，vl为对应的特征矢量。若矩阵a的特征方程为则称该矩阵为多项式p(x)的友矩阵(companionmatrix，简称友阵)，因此，多项式方程p(λl)＝0的解为其友阵a的特征方程|a-λl·1n|＝0的解。

若多项式p(x)的友阵为

则由矩阵a的特征向量构成的矩阵为范德蒙德(vandermonde)矩阵为

且有

p(λl)＝|a-λl·1n|＝0。(115)

由式(28)、式(99)及式(100)得

因s＝8，应用式(1)计算的复杂度为8·8！＝322560；而应用式(5)进行二次分块的行列式计算，其中：2·2分块矩阵计算复杂度为4！(2·2！+2·2！+1)/(2！2！)＝30，4·4分块分矩阵计算复杂度为8！(30+30+1)/(4！4！)＝4270。一般情况下，式(116)是关于τ1的16阶单项式方程。

该方法的过程表明：整体与局部、复杂与简单是对立统一的；式(4)将矢量多项式的行列式计算转化为三个矢量的行列式，这一步骤起到了决定性的作用；轴不变量及其导出的不变量都是结构参量，系统方程是关于结构参数的矢量与关节变量(标量)的矢量代数方程。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变形，这些改进和变形也应视为本发明的保护范围。