快速求取电力系统节点阻抗矩阵的高斯-约当因子表法的制作方法

本发明属于电力系统分析计算领域，涉及一种快速求取电力系统节点阻抗矩阵的高斯-约当因子表法。

背景技术：

在电力系统求解常系数方程的分析计算中，经常会用到派生于高斯消元法(高斯法)的因子表法(高斯因子表法)和高斯-约当消元法(约当法)，没有任何文献提及或应用派生于约当法的高斯-约当因子表法(约当因子表法)。此外，传统的求解电力系统节点阻抗矩阵z的方法一般有支路追加法、ldu三角分解法(ldu法)，极个别文献介绍用高斯法或高斯因子表法，但所有这些方法中均未考虑应用z阵和单位矩阵e元素结构的特点来简化计算。此外，未见文献提及应用约当法求解z阵，更没有任何文献提及应用约当因子表法求解z阵。本发明方法的主要目的就是提出约当因子表法，并将其用于求解z阵。

传统的高斯因子表法是对a阵不变、仅f阵变化的方程ax＝f进行含规格化的按行高斯消元后可得a^(n-1)′x＝f^(n-1)′，将a^(n-1)′阵对角元取倒构成高斯因子表。高斯因子表法就是根据其对角元素和下三角元素对后续不同的f阵元素f1，f2，…，fn进行前代计算，求取不同的f^(n-1)′阵元素.f1⁽¹⁾，f2⁽²⁾，…，fn⁽ⁿ⁾，再根据因子表的上三角元素和f^(n-1)′阵元素进行回代计算，求取不同的x阵元素x1，x2，…，xn。

如对四阶ax＝f方程，高斯因子表+f阵求解f⁽³⁾′阵元素的按行前代计算过程如下：

对n阶矩阵则有fi^(k)＝fi^(k-1)-li，kfk^(k)和fi⁽ⁱ⁾＝fi^(i-1)dii，(i＝1，2，…，n；k＝1，2，…，n-1)。

高斯因子表+f⁽³⁾′阵求解x阵的按行回代计算过程如下：

对n阶矩阵则有

求解线性方程组，高斯法一般是对下三角消元，既有前代也有回代；约当法的计算原理与高斯法极为相似，但同时对上下三角消元，只有前代没有回代，因此约当法的计算过程更显简单。但由于高斯法的广泛应用，使得高斯因子表法也得以广泛应用。而约当法的应用和分析不多，更没有文献提及或应用约当因子表法。深入分析可以发现，由于高斯法和约当法计算过程的不同，必定导致高斯因子表法和约当因子表法计算过程和计算效率的不同。

传统方法求解z阵时均按(k＝1，2，…，n)的顺序将对一个方程yz＝e中n*n阶z阵的求解转换成对n个方程yzk＝ek中n个zk阵的求解，即将y阵与ek阵分别构成n个n+1阶的增广阵，分别求解n个zk阵中的全部元素，从而得到整个z阵。这种求解方式也需反复对整个ek阵元素进行前代、对整zk阵元素进行回代，很难利用z阵元素的对称性进行计算，也由于没有考虑e阵元素结构的特点，需求解ek阵中的全部元素，或如传统ldu法的中间矩阵wk、hk的计算无法简化，因此计算过程繁琐、计算速度慢。

上述过程表明高斯因子表法等传统方法在形成和求解的过程中存在以下几个问题：①按行消元形成因子表的过程难以应用y阵对角元以右元素和对角元以下元素的比例对称关系实现元素的对称计算以减少计算量；②消元计算中须使用消元计算公式，不利于计算过程的理解和编程；③形成因子表后再对对角元取倒，其规格化过程中仍有大量的除法计算影响计算速度；④形成因子表后对f阵元素的按行前代计算方式也导致其效率低于按列前代计算方式，无法继续扩展应用；⑤当f阵为e阵和x阵为z阵时，由于对f阵的前代计算和对x阵的回代计算分开进行，由于未能综合考虑e阵和z阵元素结构的特点以及对zk阵和zk阵元素的求解顺序，因此无法简化对ek阵和zk阵元素的计算，也很难利用z阵元素的对称性进行计算；⑥求解z阵时，既有前代过程也有回代过程。

直接用传统约当法求解z阵也有几个问题：①约当法一般是求解变系数方程，而z阵是常系数方程；②至今没有文献介绍用约当法或约当因子表法求解z阵；③传统ldu法将求解一个n阶方程分解成求解n个n*(n+1)阶方程，若约当法也如此，则计算过程繁琐复杂；④传统约当法的规格化过程中未先将对角元素取倒，以下消元过程计算速度的提高；⑤传统约当法对上下三角消元时均按从左到右的顺序，计算效率不高；⑥传统约当法求解对称方程时未能利用元素的对称性等等。

因此，若用约当因子表法求解z阵，则在需针对前述所有问题的基础上，提出约当因子表法，然后根据其特点快速求解z阵。

技术实现要素：

为了克服上述现有技术的不足，本申请提出用一种快速求取电力系统节点阻抗矩阵的高斯-约当因子表法，其技术特征主要包括以下步骤：

步骤1：读入n节点系统的y阵数据；

步骤2：以逐行规格化、按列消元方式，用四角规则对y阵进行快速对称约当消元得约当因子表y⁽ⁿ⁾″；

(1)以逐行规格化、按列消元方式从左至右、从上而下进行约当消元形成约当因子表y⁽ⁿ⁾″阵；

高斯因子表法对式(1)的y阵元素是以按行消元、逐行规格化的方式形成高斯因子表y^(n-1)′阵，而按行消元方式的计算效率远远低于按列消元方式。本发明方法是以逐行规格化、按列消元方式从左至右、从上而下进行约当消元形成式(2)的约当因子表y⁽ⁿ⁾″阵。此处式(2)暂未考虑元素的对称算法。

(2)用四角规则对y阵元素进行约当消元获得约当因子表；

高斯因子表法中因子表的形成过程中必须应用高斯消元计算式式(3)，对于计算过程的理解和编程极其不易。本发明方法的约当消元过程直接用四角规则完成对y阵上下三角元素的约当消元计算而获得约当因子表，将复杂的消元计算公式转化成简单的对元素几何位置的操作，大大简化对计算过程的理解和编程；

假设对第k行元素规格化前后和对第k列元素约当消元前后的简化矩阵以及消元过程中参加计算的各元素位置始终如式(4)，可定义各变量为：

对角元素(终值，参考元素)；

规格化前交叉元素^(k-1)(后^(k)，终值)，对角元素同行以右；

下三角消元元素(上三角，终值)，对角元素同列以下或以上；

下或上三角计算元素的前值^(k-1)(新值^(k))，与消元元素同行、交叉元素同列的交叉点上。

式(4)表明，以对角元为参考元素，交叉元素上下同列、消元元素以右同行在交叉点上的元素都是需要计算的计算元素。式(4)同时表明的计算规律为：计算元素的“新值”等于其“前值”减去对角元之下或之上的“消元元素”乘以对角元之右的“交叉元素”。根据该规律可直接写出以下计算式。

需计算的下三角元素：

需计算的上三角元素：

上述结果与用式(3)计算的结果完全一致，因此无需应用式(3)的消元计算公式可直接完成消元计算。由于对角元素、交叉元素、消元元素、计算元素四个元素正好在矩形的四个角上，因此称为四角规则。四角规则实质上是把复杂的消元计算过程形象化，直接根据元素在矩阵的位置写出消元计算等式，大大简化对计算过程的理解和编程。

(3)对第i行元素规格化以前，先将第i行对角元素取倒，再对其右侧的元素规格化；

高斯因子表法是形成因子表后再将所有对角元素取倒，只能提高形成因子表后的计算效率，不能提高形成因子表过程中的计算效率。本发明方法是对第i行元素规格化以前，先将第i行对角元素取倒，再对其右侧的元素规格化，可同时提高形成因子表过程和形成因子表后的计算效率；

为此将式(3)中元素的规格化计算式修改为式(5)。

(4)对上三角第i列消元元素消元，计算消元元素以右的所有元素；

高斯因子表法对上三角元素不消元，因此在后续计算中有回代计算过程。本发明方法也无需消元计算公式、直接用四角规则对上三角元素消元，不但便于上三角元素消元过程程序的编写，而且在后续计算中由于没有回代计算而简化了计算过程。如对式(4)中上三角元素消元，也可直接用四角规则写出元素的计算式。

(5)利用y阵元素的对称性，分别根据第i行对角元素以右交叉元素规格化前的值赋值获得第i列对角元素以下消元元素的值，再对下三角第i列消元元素消元，仅计算消元元素右侧各行中包括对角元素的上三角元素，并依此循环；

高斯因子表法对式(4)中下三角元素消元，需分别计算消元元素以右的所有四个元素。本发明方法对下三角元素消元，可利用y阵元素的对称性仅计算消元元素右侧包括对角元素的上三角元素，而下三角元素是通过上三角元素规格化前的值赋值获得。如本方法仅需计算其以右包括对角元素的上三角的三个元素，不计算元素。元素是在对第j行元素规格化前，通过元素赋值得到。

将(1)中未考虑元素对称算法右下式的约当因子表y⁽ⁿ⁾″阵重写为如式(6)，而按对称计算方法的约当因子表y⁽ⁿ⁾″阵为如式(7)。式(7)的特点是除第一列元素外，所有下三角元素由于只有一次赋值计算，所以其下标均为1。因此对称计算方法可大大简化下三角元素计算。

本发明方法的计算过程可归纳为：对第i列元素消元前，先将第i行对角元素以右规格化前的元素分别赋值给第i列对角元素以下元素→将第i行对角元素取倒，对第i行元素规格化→对第i列对角元素以上元素消元，计算消元元素以右的所有元素→对第i列对角元素以下元素消元，仅计算消元元素以右、包括对角元素的上三角元素→继续将第i+1行对角元素以右规格化前的元素分别赋值给第i+1列对角元素以下元素→依此循环，直至形成约当因子表。

步骤3：根据约当因子表y⁽ⁿ⁾″阵和ek阵元素结构的特点，按第n～1列的顺序分别以按列前代方式求取阵对角元素及以上元素，进而直接获得zk阵对角元素及以上元素，然后根据zk阵元素的对称性求出对角元素zkk以左的元素zk，k-1～zk1；

(1)按第n～1列顺序，根据y⁽ⁿ⁾″和ek阵元素结构的特点分别以按列前代方式求取阵对角元素及以上元素进而分别根据方程，分别直接获得zn、---、zk---、z1阵。

(2)根据y⁽ⁿ⁾″阵对ek阵以按列前代方式求取阵对角元素及以上元素时，每列均需先用y⁽ⁿ⁾″阵中的对角元素dii计算ek阵中相应行的元素再从上往下用其非对角元素u、，计算该ek阵中其余的相应元素。

(3)对求得的zn、---、zk---、z1阵，按zkk～z1k顺序仅求取zk阵对角元素zkk及以上元素zk-1，k～z1k，并利用ek阵元素结构的特点简化对阵元素的计算，同时利用对称性求出zk阵对角元素zkk以左的元素zk，k-1～zk1。

传统法求取z阵时均按第1～n列顺序求取zk阵，并且未利用ek阵元素结构的特点计算，因而需求取各个ek阵和zk阵的所有元素e1k～enk和z1k～znk，因此很难实现zk阵元素的对称计算以及对ek阵元素的简化计算。

(4)求解阵时也只需求解其对角元素及其以上元素，阵对角元素以下元素均可根据前面的计算结果按对称性得到，大大简化对阵的计算。

(5)求解阵元素仅需用到y⁽ⁿ⁾″阵第k～n列的元素，其中仅用y⁽ⁿ⁾″阵第1～k行的全部元素、以及第k+1～n-1行中第k～k+1列的全部元素和第k+2～n-1列中其列号作为起始行号到第n-1行中的所有元素，进一步简化对阵元素的计算。

求解阵元素仅需用到y⁽ⁿ⁾″阵中式(8)所示a区的所有元素和b区的部分元素。

此处式(8)中应用了元素的对称算法，但为分析方便，仍然用传统方法表示。

(6)由于采用按列消元，虽然要求按第n～1列顺序求取zk阵，且求解阵元素需用y⁽ⁿ⁾″阵第k～n列的元素，但需按第k～n列的顺序用y⁽ⁿ⁾″阵元素求解阵元素。因此，对y⁽ⁿ⁾″阵第k～k+1列，需用其第1～n-1行的全部元素；对其第k+2～n列，需分别用其列数减1、减2、---、减n-1-k，其规律如式(8)所示。

实施例1：将下列四阶y4阵约当消元后所形成的约当因子表阵中的下三角元素、对角元素、上三角元素分别用l、d、u表示，且d为已经取倒的对角元素，即分别用阵以按列前代方式对e4～e1阵求解阵，即分别求解z4～z1阵的计算过程为例，说明约当因子表法的计算过程。

(1)用阵对e4阵以按列消元方式计算，每列均先用阵的对角元素d对e4阵的相应元素规格化，如下表中的“■”部分，再从上往下用其非对角元素u、l对e4阵的相应元素消元，所求得的阵。计算过程如表1。

表1用阵对e4阵求取阵计算过程

由上表可以看出，对阵第1～3列元素的计算并未改变元素的初始状态，只有第4列元素的计算才改变了其初始状态，即只有阵的第4列元素对阵元素的计算有效。因此，如果考虑e4阵元素结构的特点，则在求取阵元素时只需考虑阵第4列元素对其影响，而无需考虑阵第1～4列的所有元素对阵的计算。所以，利用e阵元素结构的特点可大大减少对其元素的计算。且由于约当消元结束后此时所求出的阵元素就是z4阵元素，因而可再根据对称性得对角元素z44以左的所有元素z43、z42、z41。

(2)用阵对e3阵以按列消元方式计算，每列均先用阵的对角元素d对e3阵的相应元素规格化，如下表中的“■”部分，再从上往下用其非对角元素u、l对e3阵的相应元素消元，所求得的阵。计算过程如表2。

表2用阵对e3阵求取阵计算过程

如果不考虑e3阵元素结构的特点，则求取阵时同样要计算e3阵中所有元素。

由于z3阵对角元素以下元素z43可直接根据z4阵的z34元素由对称性获得，因此在求取阵元素时，可不用计算其对角元素以下的元素

由上表可以看出，对阵第1～2列元素的计算并未改变阵中元素的初始状态，只有其第3～4列元素的计算才会改变其元素的初始状态，即只有阵的第3～4列元素对阵元素的计算有效，且元素无需计算。因此只需计算阵中第3～4列对角元素及其以上元素。且由于所求出的阵对角元素及其以上元素就是z3阵元素，同样可根据对称性得对角元素z33以左的元素z32、z31。

上述计算过程表明，对于zk阵，只需计算其对角元素及其上元素，其对角元素以下的元素均可根据前面zk+1～zn阵计算所得元素的对称性直接得到。因此对ek⁽ⁿ⁾″阵元素的求解实际上也是对ek⁽ⁿ⁾″阵中对角元素及其以上元素的计算。

(3)用阵对e2阵以按列消元方式计算，每列均先用阵的对角元素d对e2阵的相应元素规格化，如下表中的“■”部分，再从上往下用其非对角元素u、l对e2阵的相应元素消元，所求得的阵。计算过程如表3。

表3用阵对e2阵求取阵计算过程

z2阵中对角元素以下的元素z32、z42可直接根据z3、z4阵中的z23、z24元素由对称性获得，因此在求取阵元素时，可不用计算其对角元素以下的元素

在对对角元素及其以上元素的计算中，由于e2阵元素的特点，只有阵的第2～4列元素对阵元素的计算有效。由于所求阵就是z2阵。再根据对称性，可得出对角元素z22以左的所有元素z21。

(4)用阵对e1阵以按列消元方式计算，先用阵的对角元素d11对e1阵的相应元素规格化，如下表中的“■”部分，再从上往下用其非对角元素u、l对e1阵的相应元素消元，所求得的阵。计算过程如表4。

表4用阵对e1阵求取阵计算过程

此时所求阵就是z1阵，且只需求取阵的对角元素而不用计算其对角元素以下的元素即z1阵中对角元素以下的元素z21、z31、z41可直接根据z2、z3、z4阵中的z12、z13、z14元素由对称性获得。由上表可以看出，由于e1阵元素的特点，阵的第1～4列元素对阵元素的计算均有效，但同列以下的元素均不用计算，而同列以下的元素则根据需要计算。

上述计算分析过程表明，利用e阵元素结构的特点，用y⁽ⁿ⁾″阵求取阵元素的前代计算规律为：①由于对zk阵只需求解对角元素及其以上元素，所以对ek阵求解阵时也只需求解其对角元素及其以上元素，阵对角元素以下元素均可根据前面的计算结果按对称性得到，可简化对阵元素的计算；②求解阵元素仅需用到y⁽ⁿ⁾″阵第k～n列的元素，其中仅用y⁽ⁿ⁾″阵第1～k行的全部元素、以及第k+1～n-1行中第k～k+1列的全部元素和第k+2～n-1列中其列号作为起始行号到第n-1行中的所有元素，可进一步简化对阵元素的计算；③对ek阵元素以按列消元方式计算，每列均先用y⁽ⁿ⁾″阵的对角元素d对ek阵的相应元素规格化，再从上往下用其非对角元素u、l对ek的相应元素消元，所求得的阵；④用y⁽ⁿ⁾″阵元素用第k列的对角元素dkk对ek阵的相应元素规格化使其由1变为dkk，再从上往下用其第k列的非对角元素u、l对ek的相应元素消元，此时第k列元素的新值为其相应的u元素分别乘以阵中对角元素dkk的负值；⑤所有的消元计算都可用四角规则直接完成，而无需消元计算公式；

步骤4：将z阵写入数据文件以备后续程序使用。

本发明方法的有益效果为：

(1)提出约当因子表法，为求解常系数方程提供更多的选择方法。

(2)将约当因子表法用于求解z阵，加快z阵的求解速度。

(3)在约当因子表法中应用四角规则直接完成消元计算，无需任何消元计算公式。

(4)规格化前将对角元素取倒，大大减少程序中的除法运算。

(5)形成约当因子表对下三角元素消元时，仅计算该行的对角元素和上三角元素，而通过y阵元素的对称性获得下三角元素，大大加快前代计算速度；对上三角元素消元时，需计算该消元元素以右的所有元素。

(6)利用e阵元素结构的特点，求取zk阵或阵时仅用约当因子表y⁽ⁿ⁾″阵第1～k行中第k～n列的全部元素、以及第k+1～n-1行中第k～k+1列的全部元素和第k+2～n-1列中其列号作为起始行号到第n-1行中的所有元素，即该部分的计算以步长为“-1”按等差级数从第k+2行到第n-1行逐渐变为零值，可进一步简化阵运算的计算，并提高其前代计算速度。

(7)对zk阵或阵只需求解对角元素及其以上元素，其对角元素以下元素均可根据前面的计算结果按对称性得到。

(8)省去了约当因子表法的回代计算，计算过程更为简便。

附图说明

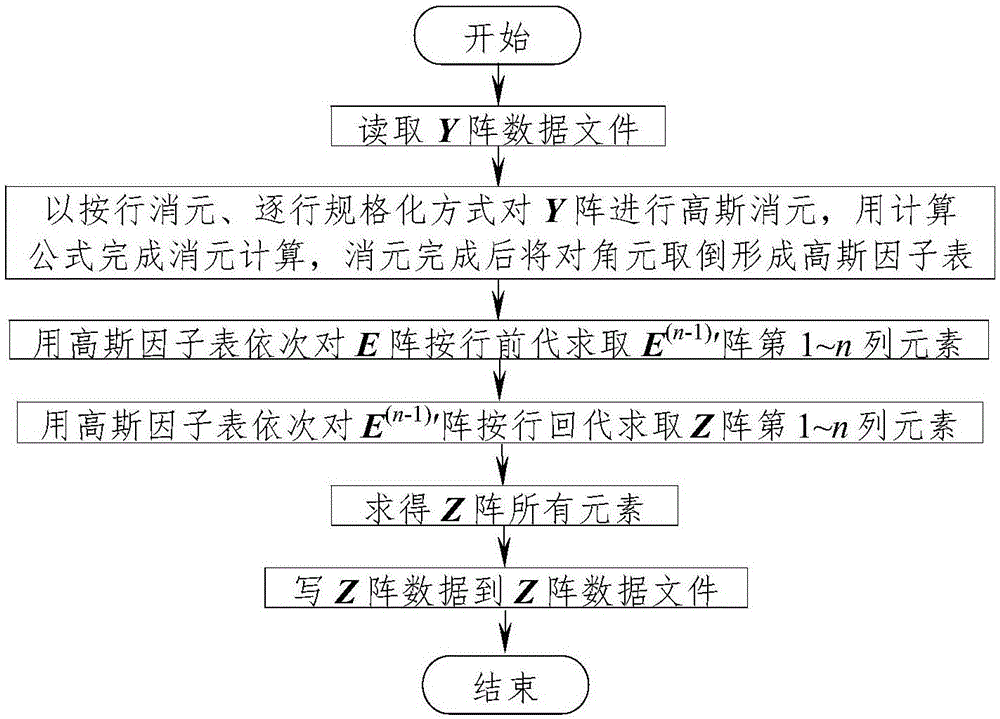
图1传统高斯因子表法求取z阵元素流程图。

图2本发明方法求取z阵元素流程图。

具体实施方式

实施例：本方法可通过实施例进一步说明。分别用高斯因子表法和本发明方法对ieee-14、-30、-57、-118节点系统的y阵求其z阵元素，并比较其计算过程的平均计算时间。计算结果如表5所示。

表5高斯因子表法和本发明方法求取z阵计算时间的比较

上述计算结果表明，本发明方法的计算速度明显快于传统的高斯因子表，计算速度约提高45％。本方法可以采用任何一种编程语言和编程环境实现。这里采用c++编程语言，开发环境是devc++。