一种有限元瞬态热分析区域分解求解方法与流程

本发明属于三维瞬态热传导有限元数值求解技术领域，具体涉及一种有限元瞬态热分析区域分解求解方法。

背景技术：

随着集成电路尺寸越来越小、设计越来越复杂、功率密度越来越高、热耗越来越大，如何快速、高效地处理产生的热量，正在成为电路电流和未来集成电路设计的最重要瓶颈。常用的热分析数值计算方法，包括有限元法、边界元法、有限差分法、热网络法等，它们都有着各自的局限性，但有限元法由于其离散复杂结构的方便变得较为突出。然而即便将有限元法用于当前多尺度的复杂电路模型，它也面临着巨大的挑战。

区域分解法(domaindecompositionmethod)是一种专门解决大型偏微分方程的数值方法，它可以将计算区域分成多个子区域，将原问题转化为定义在各个子区域上的一系列简单问题进行求解，从而将问题由大化小、由繁化简，并且特别适合进行并行计算。目前处理瞬态热传导问题的有限元区域分解算法主要有两种，一种方式是采用拉格朗日乘子法的mortar有限元法，该方法会增加有限元未知量的个数，并且最终形成对称不定的鞍点矩阵，不易于求解；另外一种是基于罗宾(robin)传输边界条件的内罚(interiorpenalty(ip))区域分解法，但这种方式要计算交界面上的热通量，并且最终形成的矩阵是非对称矩阵，同样不易于求解。

技术实现要素：

针对上述存在问题或不足，为解决现有处理瞬态热传导问题的有限元区域分解方法在实际应用中效率低下和不易于求解的问题，本发明提供了一种有限元瞬态热分析区域分解求解方法，开创性地采用接触热阻等效的传输边界条件代替传统的robin传输边界条件，将其引入到区域交界面的区域耦合计算过程，并采用interiorpenalty(ip)的方式，得到区域分解的有限元弱形式。

其具体技术方案，包括以下步骤：

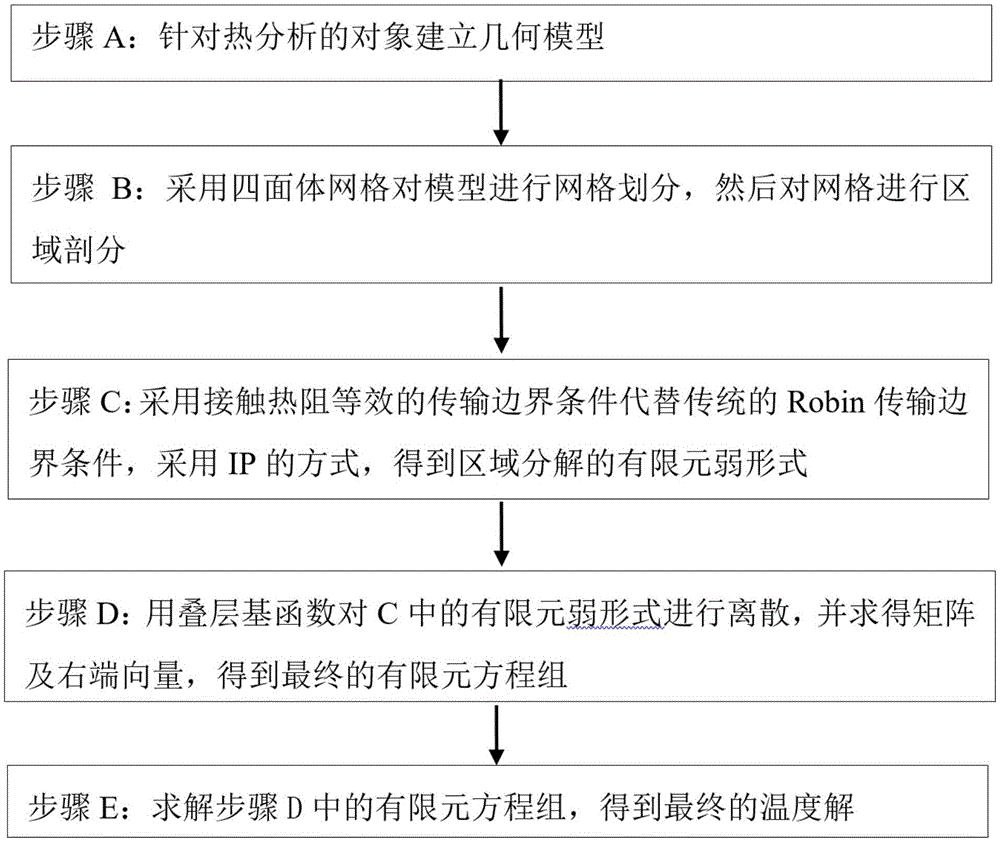
a.针对热分析的对象建立几何模型；

b.采用四面体网格对模型进行网格划分，然后对网格进行区域剖分；

c.采用接触热阻等效的传输边界条件代替传统的robin传输边界条件，采用ip的方式，得到区域分解的有限元弱形式；

对于单位面积的交界面，接触热阻定义如下：

其中r表示接触热阻，ua、ub表示接触面两侧温度，q”表示平均热流密度，文字表述为：接触热阻等于两个接触面温度之差除以平均热流密度。

通过ip方式，将接触热阻问题转化为边界条件之后，得到最终的有限元弱形式为：

其中为拉普拉斯算子，k1、k2为热传导系数，v1和v2为权函数，u1和u2为温度，q1、q2为内部产热量，δc为接触热导(接触热阻的倒数)，ρ1、ρ2是密度，c1、c2是比热容，t是时间，ω1、ω2表示求解域，γ为区域接触面，h1、h2为对流换热系数，ua1、ua2为对流换热温度。

d.用叠层基函数对步骤c中的有限元弱形式进行离散，并求得矩阵及右端向量，得到最终的有限元方程组。

e.求解步骤d中的有限元方程组，得到最终的温度解。

本发明在步骤c中，将接触热阻等效的传输边界条件代替传统的robin传输边界条件，通过考虑接触热阻的定义以及在接触面上的热通量对于接触面两侧来说是相同的(接触面两侧的温度通过改变接触热导值可以近似相同)这两点，开创性地将其转化为区域交界面传输条件，进而用有限元方法进行处理。

综上所述，本发明从接触热阻的本质出发，接触面上的热通量是连续的，两侧的温度不连续，但是运用其接触热导值的本质意义——衡量接触面两侧温度差值的大小，当其足够大时，可以保证两侧的温度值连续，将这种思想运用到区域分解交界面上，以代替传统的robin传输边界条件。本发明最大的优势就是可以简单有效地实施区域分解算法来求解大型多尺度瞬态热传导问题，而且最终求得的矩阵是对称正定矩阵，非常易于求解，可以在实际工程领域广泛应用。

附图说明

图1是本发明的流程图；

图2是两个区域的区域分解示意图；

图3是四节点四面体单元示意图；

图4是区域交界处四面体单元计算示意图。

具体实施方式

下面结合附图和具体实施例来详细描述本发明的技术方案。

一种有限元瞬态热分析区域分解求解方法，包括以下步骤：

a.针对热分析的对象建立几何模型。

b.采用四面体网格对模型进行网格剖分，将连续的几何结构空间转化为离散的网格空间，然后对网格进行区域剖分，最终将模型分成若干互不相交的子区域。

c.采用接触热阻等效的新型传输边界条件代替传统的robin传输边界条件，将其引入到区域交界面的区域耦合计算过程，并采用ip的方式，得到区域分解的有限元弱形式。

考虑三维瞬态热传导问题，其控制微分方程具有如下形式:

其中u代表在有限区域上随时间变化的温度分布，为拉普拉斯算子，k为热传导系数，q为内部产热量，ρ是密度，c是比热容，t是时间，ω表示求解域。

此外，为了求解上述问题，还必须定义其边界条件，以及初始温度场值。这里考虑对流边界条件：

u(x,y,z；t)|t＝0＝u0(x,y,z)(5)

为了简便描述，这里将求解域分为两个区域，进而考虑两个区域接触面上的接触热阻。就如图2中所示的那样：ω:＝ω1∪ω2，将表示子域的接触面表示为外部边界定义为另外，表示单位法向量，方向是在边界γ上指向区域ωi外部。为了更好地描述，这里定义体积分和面积分:

(u,v)ω＝∫ω(u,v)dv(6)

<u,v>γ＝∫γ(u,v)ds(7)

其中u、v表示任意两个函数，v表示体积，s表示面积。

上述三维瞬态热分析边值问题就可表示为：

u1＝u2onγ(10)

由接触热阻的定义，对两个区域分别有：

其中δc是两个区域交界面上的接触热导(接触热阻的倒数)，k1,k2为两个区域的热传导系数，u1,u2为接触面上的温度，n1,n2为法线。重点说明，当接触热导δc足够大时，接触面两侧的温度连续性和热通量连续性都会得到满足，也就是公式(10)和公式(11)自然满足。这个思路也是本发明提出的接触热阻等效的新型传输边界条件的核心。

接下来采用ip方式，得到两个区域的瞬态热传导边值问题的残差表达式：

其中表示两个区域瞬态热分析控制微分方程的残差，表示两个区域交界面上接触热导表达式的残差，表示两个区域对流边界条件的残差。然后就可以得到上述残差表达式的线性组合表达式如下：

其中c1,c2,c3,c4是任意实数，v1,v2为权函数。由格林公式，可以展开为

同理可以得到：

类似地，可以将分界面上的表达式展开为：

最后，可以将对流边界上的表达式展开为：

由于c1,c2,c3,c4的任意性，令c1＝c2＝c3＝c4＝-1，最终可以将式(22)写为如下的表达式，也就是最终的有限元伽辽金弱形式：

d.用叠层基函数对c中的有限元弱形式进行离散，并求得矩阵及右端向量，得到最终的有限元方程组。

如图3所示四面体单元中i,j,k,l代表四个顶点的编号，得到四个最基本的基函数，具体推导过程为一种公知过程，这里不再阐述：

式中

将(34)式、(35)式、(36)式、(37)式中的i,j,k,l轮换，得到aj,ak,al，bj,bk,bl，cj,ck,cl，dj,dk,dl。v为四面体的体积。为了使四面体的体积不为负值，单元节点编号i,j,k,l必须依照一定的顺序。在右手坐标系中，当i,j,k的方向转动时，右手螺旋应指向l的方向。

确定了基函数为n1,n2,n3,n4，对于有限元过程来说，把域ω离散为m个单元之后，如同(29)所示的弱形式定积分，可以通过将每个单元的积分贡献简单相加即可。子区域内部单元的刚度矩阵以及对流矩阵项在很多基础的热传导有限元书中都有介绍，本发明不再赘述，下面只介绍区域交界面上的矩阵计算。其离散单元矩阵形式为：

以图4所示的两个四面体为例进行说明。交界面上的两个四面体为abcd和efgh，三角面bcd和efg是同一个面，即其区域交界面。区域交界面上的矩阵可以分成两部分，一部分是子区域内部矩阵一部分是耦合矩阵可以写为如下的表达式

其中γbcd、γefg分别表示三角面bcd和三角面efg，代表三角面bcd的基函数，代表三角面efg的基函数，按照上面的公式就可以建立交界面两侧之间的关系矩阵。

e.求解步骤d中的有限元方程组，得到最终的温度解。

在步骤d中已经求得有限元的子区域矩阵、区域之间的耦合矩阵和右端向量，可以形成最终的线性方程组，有很多方法可以进行方程组的求解，直接法和迭代法都在很多文献资料里有详细的论述，本发明不再进行具体描述。求解完有限元方程组，就得到了最终的温度解，可以发现区域交界面上温度场是连续的。

综上所述，可见本发明针对当前区域分解方法用于求解瞬态热传导问题的弊端，将接触热阻的思想引入到区域分解的传输条件中，代替传统的robin传输边界条件，配合有限元方法进行数值求解，可以简单有效地实施区域分解算法来求解大型多尺度瞬态热传导问题，而且最终求得的矩阵是对称正定矩阵，非常易于求解，可以在实际工程领域广泛应用。