基于跨维马尔科链蒙特卡罗的自适应多项式回归方法与流程

本发明属于信号处理技术领域，具体涉及基于跨维马尔科夫链蒙特卡罗(trans-dimensionalmarkovchainmontecarlo,tdmcmc)的多项式回归方法，其方法可以用在很多需要自适应确定多项式最优阶次的数据处理问题中。

背景技术：

回归分析(regressionanalysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。多项式回归是回归分析中的重要方法，用于很多领域。经典的多项式回归问题其实仍是一个难点问题，主要是给定已知的数据点多项式阶次的选择仍比较难，而过去常常是多项式阶次假设已定情况下进行多项式的拟合或回归分析，如果多项式阶数过高，会出现过拟合的现象；多项式阶数过低，不能很好的对数据进行回归。因此，研究能够自适应确定多项式阶数的多项式回归方法在该领域进行广泛和深入的研究具有极其重要的意义。

技术实现要素：

为克服上述现有技术的不足，本发明的目的在于提供基于跨维马尔科夫链蒙特卡罗的自适应多项式回归方法，实现一种可以自适应地确定多项式的阶次以及系数，采用基于跨维马尔科夫链蒙特卡罗(trans-dimensionalmarkovchainmontecarlo,tdmcmc)方法能够对参数进行跨维寻优，实现多项式阶次和多项式系数的联合估计。

为了实现上述目的，本发明采用的技术方案是：

基于跨维马尔科夫链蒙特卡罗的自适应多项式回归方法，其特征在于，包括以下步骤：

首先，建立含有多项式阶次和多项式系数参数的图模型，即建立包含多项式阶次和多项式系数的贝叶斯模型；

然后，针对多项式回归问题，提出出生和死亡两种跨维的参数状态转移策略及一个不变维的参数更新策略；而后，基于跨维马尔科夫链蒙特卡罗方法，基于给定数据样本，实现多项式回归模型阶次和多项式系数的联合寻优；

具体的跨维转移核策略是：多项式阶次变高，对应出生过程，模型变为m+1阶，新生成第m+1阶的多项式系数；多项式模型阶次变低，对应死亡过程，多项式模型由m阶变为m-1阶，此时多项式其他系数不变。

所述的基于跨维马尔科夫链蒙特卡罗的自适应多项式回归方法，包括以下步骤：

步骤1，建立有向无环概率图模型，用于对多项式回归问题中多项式系数向量a和方差σ²等未知参数后验推理的贝叶斯模型描述；

步骤2，提出出生和死亡两种跨维的参数状态转移策略及一个不变维的参数更新策略；具体如下：

1)出生过程

多项式的回归问题中，设计的出生过程是指多项式的阶次增加1的过程，即相对于原有的m阶多项式，多出生一个高阶项x^m+1，因此，多项式的阶次由m变为m+1，多项式的系数也多了一个，每次出生的多项式首次系数先选取为1，而后基于更新策略更新，若最高次项系数小于某个较小值，则舍去；

2)死亡过程

多项式的回归问题中，死亡过程是指多项式的阶次减1的过程，即相对于原有的m阶多项式，舍去最高阶项x^m，因此，多项式的阶次由m变为m-1，多项式的系数也少了一个，多项式的其他低阶系数保持不变；

3)不变维时多项式系数更新过程

除了出生和死亡两个跨维的参数转移策略外，多项式的系数更新过程是基于gibbs抽样实现的，具体过程如下：

a、第i步迭代时，

利用式(5)抽取多项式系数a＝[a1，a2，a3，…，am]^t，

a|(xm,y,σ²,δ²)～n(f,σ²h)(5)

式中，m是当前多项式的阶数，a是多项式的系数向量，xm是自变量x针对不同次幂组成的m项多项式的各项的值，y是多项式对应各自变量输入的多项式函数值；假设的多项式拟合的误差符合高斯分布，σ²是零均值误差的方差，δ²是一个尺度参数，式(5)中，h＝(a^ta+∑^-1)^-1，f＝hxmy，此处，∑^-1＝δ^-1xm^txm；；

利用式(6)抽取σ²值，

式中，σ²是零均值误差的方差，v0和γ0是假设方差参数σ²符合逆伽马分布的两个超参数，n是自变量样本个数；xm是自变量x针对不同次幂组成的m项多项式的各项的值，y是多项式对应各自变量输入的多项式函数值；δ²是一个尺度参数,p＝in-xmhxm^t，in是n阶单位矩阵，

利用式(7)抽取参数δ²值，

式中，xm是自变量x针对不同次幂组成的m项多项式的各项的值，y是多项式对应各自变量输入的多项式函数值；δ²是一个尺度参数、a是多项式的系数向量、σ²是零均值误差的方差，和是假设尺度参数δ²符合逆伽马分布的两个超参数，m是当前多项式的阶数；

b、参数i值增加1，返回步骤2，直至i取值到设置的最大迭代n结束，

在此抽样过程中，算法迭代n次，前n/2次值被舍弃，后n/2次抽取的样本均值被用来作为各未知参数的估计值。

所述的步骤1中，有向无环概率图模型的建立方式如下：

未知变量表示为圆形框，已知的数据点对表示成矩形框，而方框表示的是未知参数的超参数；

对参数进行先验分布的假设：对于测量噪声ε，符合高斯噪声，设置其先验分布为零均值，方差为σ²，假设σ²符合共轭的逆伽马先验分布，即：σ²～ig(v0，γ0)，δ²是一个尺度参数，也给其假设为共轭先验分布，在这里，是超参数，给其一个固定值，参数m是回归多项式的项数(阶次)，其符合截断的泊松分布，当m取固定值时，数据矩阵xm变为已知值，多项式系数a的先验设为多元高斯分布，即：a|(δ²，σ²，xm)～n(0，σ²∑)，此处，∑^-1＝δ^-2xm^txm，式中，m是当前多项式的阶数，a是多项式的系数向量，xm是自变量x针对不同次幂组成的m项多项式的各项的值，假设的多项式拟合的误差符合高斯分布，σ²是零均值误差的方差，δ²是上文所述的尺度参数，

对于式(3)及式(4)，εi＝yi-ximai表示第i个数据样本对应的测量值和估计出的回归模型之间的误差，符合高斯分布，xim表示xm矩阵的第i行，采用如下的似然函数：

式中，n表示数据样本数，即要进行多项式回归或拟合的数据点个数，

贝叶斯多项式回归方法包括计算多项式系数a[a1，a2，a1，…，am]^t的后验分布，以及高斯噪声的方差，根据贝叶斯理论，参数的后验分布为：

上式中，p(y|a，m，σ²，x)是似然函数，p(a1，a2，…，am，m，σ²)是参数的先验分布，基于已知的离散点，估计出多项式的系数a＝[a1，a2，a3，…，am]^t。

多项式的出生和死亡转移更新过程前面已经说明，当多项式项数不变时，其未知参数的gibbs抽样更新过程，更新过程可参考步骤2中3)的采样过程，可以写出各未知参数(误差的方差、多项式系数和噪声参数δ²)的满条件分布。

与现有技术相比，本发明的有益效果是：

本发明在给定已知待回归数据，其他参数例如多项式阶次以及系数不知道的情况下，不同于现有的常见多项式回归方法；由于采用了跨维马尔科夫链蒙特卡罗方法，不仅包含多项式系数自适应更新策略，由于引入了能够实现多项式阶数增加或减少的两个跨维转移核，所以具有不仅能够自适应地确定多项式系数，而且还能够自适应确定多项式最佳阶数的优点，很好的拟合了给定的数据。在此基础上，可以将本发明提出的自适应确定多项式阶次和系数的方法应用到各个领域。

附图说明

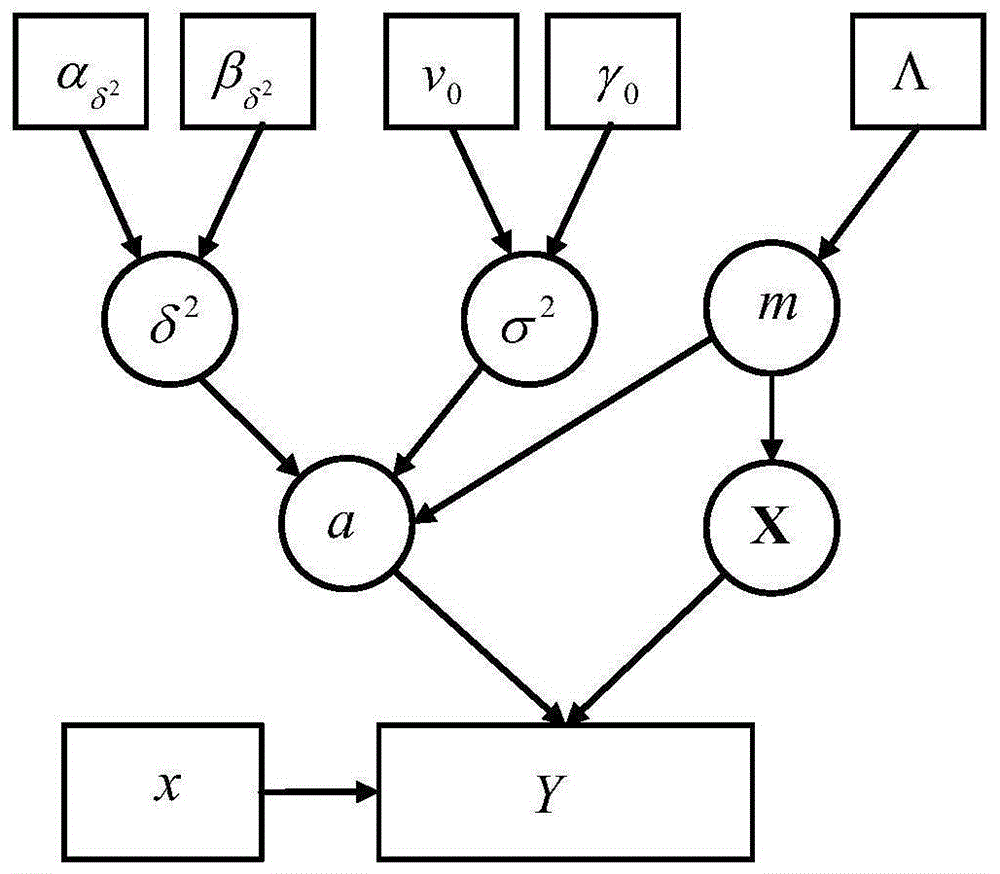
图1为本发明多项式回归的图模型。

图2为本发明的流程图。

具体实施方式

下面对本发明的具体实施方式进行详细说明。

基于跨维马尔科夫链蒙特卡罗的自适应多项式回归方法，包括以下步骤：

首先，建立(如图1所示的)含有多项式阶次和多项式系数参数的图模型，即建立包含多项式阶次和多项式系数的贝叶斯模型；

然后，针对多项式回归问题，提出出生和死亡两种跨维的参数状态转移策略及一个不变维的参数更新策略；而后，基于跨维马尔科夫链蒙特卡罗方法，基于给定数据样本，实现多项式回归模型阶次和多项式系数的联合寻优；

具体的跨维转移核策略是：多项式阶次变高，对应出生过程，模型变为m+1阶，新生成第m+1阶的多项式系数；多项式模型阶次变低，对应死亡过程，多项式模型由m阶变为m-1阶，此时多项式其他系数不变。

参见图2，基于跨维马尔科夫链蒙特卡罗的自适应多项式回归方法，包括以下步骤：

步骤1，单元多项式回归

建立有向无环概率图模型，用于对多项式回归问题中多项式系数向量a和方差σ²等未知参数后验推理的贝叶斯模型描述；

所谓的单元多项式回归，是指回归分析时由一个自由变量决定一个因变量，过去很多情况下都是基于最小二乘方法实现的，所谓的最小二乘是指由拟合的多项式估计出的输出值和原始值之间的残差的平方和最小，将式子简写表示为：

y＝xa+ε(1)

y是式(1)中的等式左边的因变量y的n维向量，x是由输入变量x组成的维数为n×(m+1)维的矩阵，a是多项式系数组成的维数为m+1的系数向量，ε如式(1)所示，是n维残差向量，若对该式基于最小二乘的策略进行优化，具体过程不在此赘述，最终得到的最优多项式系数估计结果为：

a＝(x^tx)^-1x^ty(2)

在此过程中，多项式的阶次m是事先给定的，在有些多项式回归问题中，为了比较多项式到底用多少阶多项式最好，需要进行多次不同阶次的多项式拟合，最终比较哪个最优，当数据量很大，或多项式的阶次很高时，此方法不可取；另外也容易造成过拟合情况；

步骤2，基于tdmcmc的多项式回归

本发明提出的基于tdmcmc的多项式回归策略中，除了实现不变维数的多项式的系数更新估计外，还需要实现多项式阶次的联合估计，其中涉及到跨维转移策略；针对多项式回归问题，提出出生和死亡两种跨维的参数状态转移策略及一个不变维的参数更新策略；

针对一元(一个因变量)多项式回归问题：a|(xm,y,σ²,δ²)～n(f,σ²h)，其中m为多项式的阶次，a为多项式系数。在此问题中，建立包含多项式阶次和多项式系数的贝叶斯模型，具体的迭代中，多项式的系数采用gibbs抽样策略进行更新；

具体的跨维转移核策略是：多项式阶次变高，对应出生过程(birth核)，模型变为m+1阶(最高项是m+1次幂)；多项式模型阶次变低，对应死亡过程(death核)，多项式模型由m阶变为m-1阶，此时多项式其他系数不变；在本问题研究中没有split核和merge核，具体策略如下：

1)出生过程

多项式的回归问题中，设计的出生过程是指多项式的阶次增加1的过程，即相对于原有的m阶多项式，多出生一个高阶项x^m+1，因此，多项式的阶次由m变为m+1，多项式的系数也多了一个，每次出生的多项式首次系数先选取为1，而后基于更新策略更新，若最高次项系数小于某个较小值，则舍去；

2)死亡过程

多项式的回归问题中，死亡过程是指多项式的阶次减1的过程，即相对于原有的m阶多项式，舍去最高阶项x^m，因此，多项式的阶次由m变为m-1，多项式的系数也少了一个，多项式的其他低阶系数保持不变。

3)不变维时多项式系数更新过程

除了出生和死亡两个跨维的参数转移策略外，多项式的系数更新过程是基于gibbs抽样实现的，具体过程如下：

a、第i步迭代时，

利用式(5)抽取多项式系数a＝[a1，a2，a3，…，am]^t，

a|(xm,y,σ²,δ²)～n(f,σ²h)(5)

式中，m是当前多项式的阶数，a是多项式的系数向量，xm是自变量x针对不同次幂组成的m项多项式的各项的值，y是多项式对应各自变量输入的多项式函数值；假设的多项式拟合的误差符合高斯分布，σ²是零均值误差的方差，δ²是尺度参数，其详细参数见下文对图模型的详细说明；式(5)中h＝(a^ta+∑^-1)^-1，f＝hxmy，此处，∑^-1＝δ^-1xm^txm；

利用式(6)抽取σ²值，

式中，σ²是零均值误差的方差，v0和γ0是假设方差参数σ²符合逆伽马分布的两个超参数，n是自变量样本个数；xm是自变量x针对不同次幂组成的m项多项式的各项的值，y是多项式对应各自变量输入的多项式函数值；δ²是尺度参数，p＝in-xmhxm^t，in是n阶单位矩阵；

利用式(7)抽取参数δ²值，

式中，xm是自变量x针对不同次幂组成的m项多项式的各项的值，y是多项式对应各自变量输入的多项式函数值；δ²是一个尺度参数、a是多项式的系数向量、σ²是零均值误差的方差，和是假设尺度参数δ²符合逆伽马分布的两个超参数，m是当前多项式的阶数；

b、参数i值增加1，返回步骤2，直至i取值到设置的最大迭代n结束。

在此抽样过程中，算法迭代n次，前n/2次值被舍弃，后n/2次抽取的样本均值被用来作为各未知参数的估计值。

在此抽样过程中，算法迭代8000次，前4000次值被舍弃，后4000次抽取的样本均值被用来作为各未知参数的估计值。

所述的步骤1中，有向无环概率图建模及参数估计

对于前面提到的多项式回归问题，我们先建立如图1所示的有向无环概率图模型，用于对多项式回归问题中多项式系数向量a和方差σ²等未知参数后验推理的贝叶斯模型描述。

在图1中，未知变量表示为圆形框，已知的数据点对表示成矩形框，而方框表示的是未知参数的超参数。对参数进行先验分布的假设：对于测量噪声ε，符合高斯噪声，我们设置其先验分布为零均值，方差为σ²，假设σ²符合共轭的逆伽马先验分布，即：σ²～ig(v0，γ0)，δ²是一个尺度参数，也给其假设为共轭先验分布，在这里，是超参数，给其一个固定值，参数m是回归多项式的项数(阶次)，其符合截断的泊松分布，当m取固定值时，数据矩阵xm变为已知值，多项式系数a的先验设为多元高斯分布，即：a|(δ²，σ²，xm)～n(0，σ²∑)，此处，∑^-1＝δ^-2xm^txm。

对于式(3)及式(4)，εi＝yi-ximai表示第i个数据样本对应的测量值和估计出的回归模型之间的误差，符合高斯分布，xim表示xm矩阵的第i行，给出如下的似然函数：

式中，n表示数据样本数，即要进行多项式回归或拟合的数据点个数。贝叶斯多项式回归方法包括计算多项式系数a＝[a1，a2，a3，…，am]^t的后验分布，以及高斯噪声的方差，根据贝叶斯理论，参数的后验分布为：

上式中，p(y|a，m，σ²，x)是似然函数，p(a1，a2，…，am，m，σ²)是参数的先验分布，本文的目标是：基于已知的离散点，估计出多项式的系数a＝[a1，a2，a3，…，am]^t。

多项式的出生和死亡转移更新过程前面已经说明，当多项式项数不变时，其未知参数的gibbs抽样更新过程。更新过程可参考步骤2中3)的采样过程。可以写出各未知参数(误差的方差、多项式系数和噪声参数δ²)的满条件分布；具体如下：

a|(xm,y,σ²,δ²)～n(f,σ²h)(5)

其中，上式中h＝(a^ta+∑^-1)^-1，f＝hxmy，p＝in-xmhxm^t。

各参数含义的详细说明已在前面说明，此处不再赘述。