小样本条件下水文频率分析中FrankCopula函数的参数估计方法与流程

本发明涉及一种水文频率分析中copula函数参数估计方法，尤其涉及一种小样本条件下水文频率分析中frankcopula函数的参数估计方法。

背景技术：

多变量水文频率分析是各类水利、土木工程规划、设计确定工程规模和管理决策的主要依据。构建多元水文变量的联合分布函数是多变量水文分析计算的前提和核心，copula函数能够有效描述水文事件的内在规律和特征属性之间的相互关系，能够克服传统多变量联合分布构建的缺点，已被广泛应用于洪水、暴雨等极值水文事件的联合分布构建。

然而，copula函数的参数估计作为多变量水文频率分析的关键步骤，需要大样本容量的水文序列数据。在工程水文计算领域却经常面临小样本资料的情况，主要表现在两方面：(1)一些流域基础性水文数据无法获取、部分站点实测水文资料序列较短；(2)多数水文序列资料总长度仅有40～60年，气候变化与人类活动的双重作用使得水文要素之间的关系发生显著改变，甚至发生多次突变，将水文序列划分为不同时段，导致不同时段的样本量极为稀少，某些时段甚至仅有10个样本。在工程实践中，一般认为样本容量小于等于30为小样本，而小样本条件下copula函数的参数估计研究非常匮缺，相应的研究手段和技术途径亟需改进发展。

对于frankcopula函数来说，相关性指标和极大似然估计是常用的参数估算方法。相关性指标法的基本思路为：首先求解多变量水文序列之间的kendell相关系数，然后利用kendell相关系数与frankcopula函数参数之间的关系即可得到frankcopula的参数。极大似然估计的基本思路为：根据样本构建最大似然函数，然后对各参数求偏导，并令偏导等于零组成非线性方程，最后利用数值方法(newton-raphson算法)求解上述方程(组)即可得到copula函数的参数。

根据kendall相关系数的定义易知，样本量越大，相关系数的估计越准确，相关性指标法估算参数的准确度就越高。根据极大似然估计的原理可知，样本量越大，似然函数的估计就越准确。相关研究表明：极大似然估计在样本量大于50时是可行的，样本量小于50，误差较大。因此，对于frankcopula函数来说，相关性指标和极大似然估计对资料的长度要求均很高，中小样本条件下的参数估计存在估计不准确、误差过大等问题。

技术实现要素：

发明目的：本发明提出一种针对小样本条件的高准确度frankcopula函数参数估计方法。

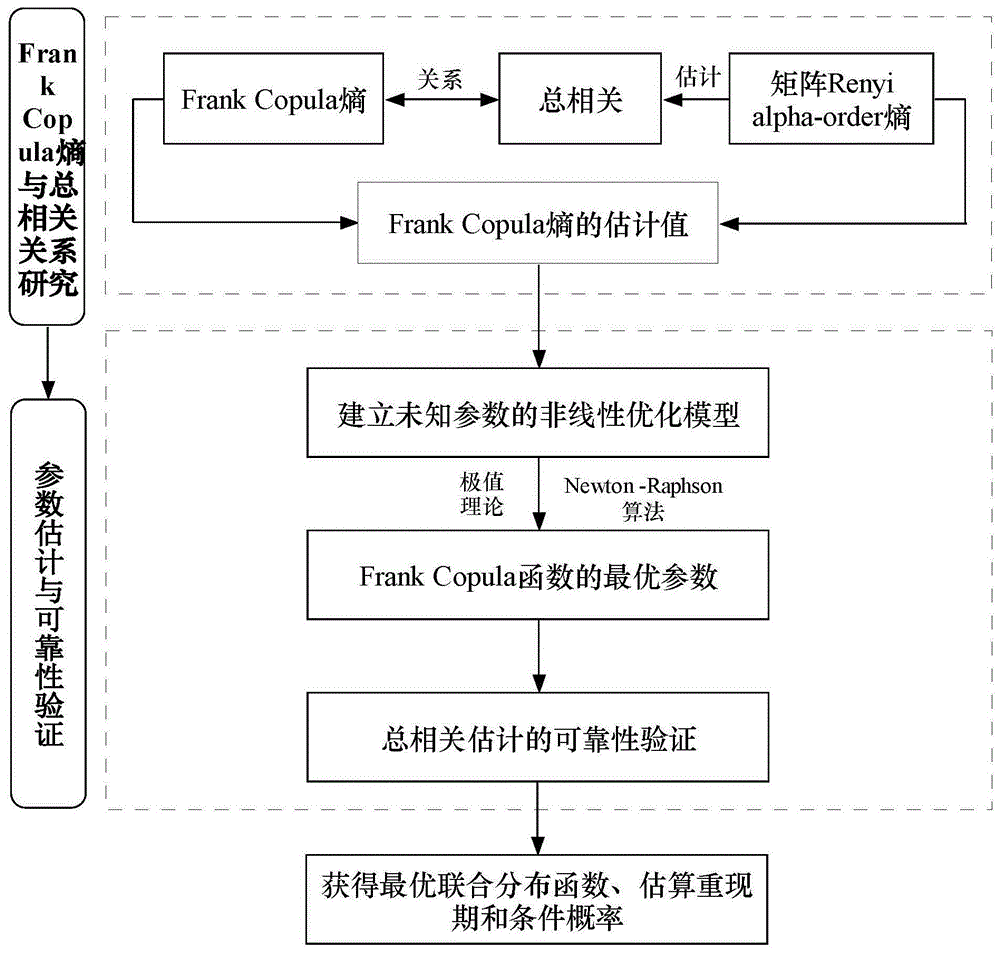
技术方案：本发明所述的小样本条件下水文频率分析中frankcopula函数的参数估计方法，包括步骤：

(1)建立frankcopula熵与多元水文变量的总相关之间的关系模型；

(2)根据矩阵renyiα阶熵理论估计多元水文变量的总相关；

(3)建立frankcopula函数的未知参数的非线性优化模型，求解得到最优参数，继而获得最优copula函数；

进一步地，所述frankcopula熵hc(u1,u2,…,uk；p)与多元水文变量的总相关tc之间的关系模型如下公式所示：

hc(u1,u2,…,uk；p)＝-tc

其中，ui＝fi(xi),i＝1,2…,k为各水文随机变量xi,i＝1,...,k对应的边缘分布函数，k为变量个数；p为frankcopula函数的未知参数，多元水文变量的总相关tc基于shannon熵计算得到。

推导过程如下：

设k维水文随机变量(x1,x2,…,xk)(其取值范围用(x1,x2,…,xk)来刻画，其中(x1,x2,…,xk)为k维实变量)的边缘分布函数分别为ui＝fi(xi),i＝1,2…,k，则frankcopula熵定义如下：

其中c(u1,u2,…,uk；p)为frankcopula的概率密度函数，p为frankcopula函数的未知参数。

设k维随机变量(x1,x2,…,xk)(其取值范围用(x1,x2,…,xk)来刻画，其中(x1,x2,…,xk)为k维实变量)的联合概率密度函数为f(x1,x2,…,xk)，边缘概率密度函数分别为fi(xi),i＝1,2,…,k，则它们的联合熵为：

根据多元微积分和概率论知识对(2)式做进一步推导：

因此，可以得到如下结论：

其中，为第i个变量的边缘熵。

设k维随机变量(x1,x2,…,xk)(其取值范围用(x1,x2,…,xk)来刻画，其中(x1,x2,…,xk)为k维实变量)之间的总相关为tc，则基于shannon熵的总相关为：

根据(3)和(4)式可知frankcopula熵与总相关之间的关系如下：

hc(u1,u2,…,uk；p)＝-tc(5)

总相关为多元变量边缘熵的和与联合熵的差，如果采用shannon熵求解多维变量的边缘熵和联合熵，需要准确模拟多维变量的边缘分布和联合分布，这对于高维稀疏的水文数据来说是非常困难的。而矩阵renyiα阶熵理论可以直接从多元水文数据序列中估计变量的边缘熵和联合熵，不需要模拟变量的边缘分布和联合分布。因此，矩阵renyiα阶熵理论可以直接从多元水文数据序列中估计总相关。

首先对有关矩阵renyiα(α＞0且α≠1)阶熵理论的基本概念进行阐述：

定义一：设为一个实数正定核且无限可分，给定(n为变量x的观测值数目)和gram矩阵k(由样本两两计算得到的正定矩阵，对于标准正定n阶矩阵a，满足tr(a)＝1，则矩阵renyiα阶熵定义如下：

其中，r和s表示矩阵的行序号和列序号，和表示第i个变量的第r个和第s个观测值，λq(a)为a的第q个特征值。

定义二：给定一个含有n个样本的集合其中上标m表示样本指标序号，每个样本含有k(k≥2)个变量x1∈χ1,x2∈χ2,…,xk∈χk，正定核分别为则k个变量的矩阵renyiα阶联合熵定义如下：

其中ai,i＝1,2,…,k表示k个矩阵，每个矩阵的元素分别为：r和s表示矩阵的行序号和列序号，和表示第i个变量的第r个和第s个观测值，表示哈达玛积。

定义三：基于矩阵renyiα阶熵的总相关定义如下：

sα(ai)为第i个变量的矩阵renyiα阶边缘熵。

因此，根据公式(6)～(8)即可估计多元水文变量之间的总相关。

进一步地，所述步骤(3)包括：

(31)将基于矩阵renyiα阶熵的总相关tcα(a1,a2,…,ak)的相反数作为frankcopula熵的估计值，建立如下非线性优化模型：

其中，c(u1,u2,…,uk；p)为frankcopula的联合概率密度函数；

(32)当式(9)取得最小值时，对应的参数即为frankcopula函数的最优参数，故令其中：

继而得到最优copula函数。

本发明所述的小样本条件下水文频率分析中frankcopula函数的参数估计方法还包括步骤：

(4)根据最优copula函数对水文数据进行估算。

进一步地，所述步骤(4)包括：根据最优copula函数构建水文变量的联合分布函数，由此计算联合重现期、同现重现期和条件概率等。

进一步地，当水文随机变量为二维时，根据如下公式计算联合重现期t1：

其中，f1(x1)为二维随机变量(x1,x2)关于x1的边缘分布函数，f2(x2)二维随机变量(x1,x2)关于x2的边缘分布函数，c(f1(x1),f2(x2)；p)为frankcopula的分布函数，p为frankcopula函数的未知参数。(x1,x2)为二维随机变量(x1,x2)的取值，x1和x2为任意实数。

进一步地，当水文随机变量为二维时，根据如下公式计算同现重现期t2：

其中，f1(x1)为二维随机变量(x1,x2)(其取值范围用(x1,x2)来刻画，其中(x1,x2)为二维实变量)关于x1的边缘分布函数，f2(x2)二维随机变量(x1,x2)关于x2的边缘分布函数，c(f1(x1),f2(x2)；p)为frankcopula的分布函数，p为frankcopula函数的未知参数。

进一步地，当水文随机变量为二维时，根据如下公式计算条件概率p(x2≤x2|x1＞x1)：

其中，f1(x1)为二维随机变量(x1,x2)关于x1的边缘分布函数，f2(x2)二维随机变量(x1,x2)关于x2的边缘分布函数，x1,x2为二维实变量，c(f1(x1),f2(x2)；p)为frankcopula的分布函数，p为frankcopula函数的未知参数。

有益效果：本发明相较于现有技术，极大地提高了小样本条件下总相关估计的准确性，具有较大的可靠性和应用潜力。

附图说明

图1为本发明实施例的方法流程图；

图2为随机生成的1000组服从frankcopula的二元水文数据序列；

图3为样本量为30时总相关估计和传统参数估计方法得到的参数与真实参数之间的相对误差比较；

图4为样本量为25时总相关估计和传统参数估计方法得到的参数与真实参数之间的相对误差比较；

图5为样本量为20时总相关估计和传统参数估计方法得到的参数与真实参数之间的相对误差比较；

图6为样本量为15时总相关估计和传统参数估计方法得到的参数与真实参数之间的相对误差比较；

图7为样本量为10时总相关估计和传统参数估计方法得到的参数与真实参数之间的相对误差比较；

图8为不同小样本情景下三种参数估计方法的平均相对误差比较；

图9为不同小样本情景下三种参数估计方法的最小相对误差比较；

图10为不同小样本情景下三种参数估计方法的最大相对误差比较。

具体实施方式

下面结合附图和实施例对本发明的技术方案作进一步的说明。

对于工程水文计算领域，经常研究年尺度上的变量，50组样本算是大样本，为此，本专利重点针对样本量小于等于30时frankcopula函数的参数估计方法进行研究。

请参见图1，其示出了本发明所述小样本条件下水文频率分析中frankcopula函数的参数估计方法。以二元frankcopula函数的参数求解为例，首先根据matlab中的copula随机数和分布反演技术生成1000组服从frankcopula的二元水文数据序列，如图2所示。本发明所述的小样本条件下水文频率分析中frankcopula函数的参数估计方法，包括步骤：

步骤1：根据shannon熵理论和多元微积分理论，构建二元frankcopula熵hc(u1,u2)与二元变量x1,x2的总相关tc之间的关系模型：

其中，frankcopula的概率密度函数c(u1,u2；p)定义如下：

u1＝f1(x1)，u2＝f2(x2)为二维水文随机变量对应的边缘分布函数；p为frankcopula函数的未知参数。

步骤2：对于1000组二元水文数据序列，分别选取不同样本容量的小样本情形，包括30、25、20、15和10，采用包含相同样本容量的窗口依次进行滑动处理，基于矩阵renyiα阶熵理论(公式(6)～(8))分别计算不同样本情形下二元水文数据序列的总相关，共计算4905次。基于矩阵renyiα阶熵的总相关方法中有两个系数需要给定，分别为内核大小σ和熵的阶数α。根据相关文献结论，σ取所有成对数据点之间欧氏距离的总(中位数)范围的10％到20％。为了接近shannon熵，α取1.01。

步骤3：构建求解frankcopula参数的非线性优化模型：

其中，tcα(a1,a2)为基于矩阵renyiα阶熵的总相关；

步骤4：根据函数极值理论可知上述非线性优化模型等价于下述方程：

令则有：

其中，

直接求解上述方程很困难，本申请利用数值方法(newton-raphson算法)进行求解，即可得到frankcopula函数的未知参数，从而得到最优copula函数。

为验证本发明方法(总相关估计)的效果，以二元frankcopula函数为例，开展总相关估计和传统参数估计方法(极大似然估计和相关性指标法)在不同数目小样本下的参数计算效果模拟实验，验证总相关估计在小样本条件下的有效性和稳健性。具体做法如下：根据生成的1000组服从frankcopula的二元水文数据序列，分别选取不同样本容量的小样本情形，包括30、25、20、15和10，采用包含相同样本容量的窗口依次进行滑动处理，frankcopula的真实参数为6.764，计算不同样本情形下三种参数估计方法的相对误差。不同小样本情形(30、25、20、15和10)分别做了971、976、981、986、991次模拟，共计4905次模拟。不同小样本情形下(30、25、20、15和10)三种参数估计方法得到的参数与真实参数之间的相对误差如图3～7所示，平均相对误差如表1～5所示。

表1

由图3可知，在30个样本下，总相关估计的相对误差在绝大部分情形下均远低于相关性指标和极大似然估计。由表1可知，总相关估计的平均相对误差、最小相对误差和最大相对误差均远低于相关性指标和总相关估计，总相关估计的平均准确率高达85.5％。综上，总相关估计具有非常满意的效果，显著优于相关性指标和极大似然估计。

表2

由图4可知，在25个样本下，总相关估计的相对误差在大部分情形下均最小，说明总相关估计的效果最好。由表2可知，总相关估计的各类误差均最小，进一步可以看出极大似然估计和相关性指标的最大相对误差均超过了140％，说明极大似然估计和相关性指标具有非常大的不确定性。综上，总相关估计得到的参数平均准确率达到84.6％，性能最好。

表3

由图5可知，当使用20个样本时，大部分情形下总相关估计均具有最小的相对误差，性能最好。由表3可知，总相关估计的平均相对误差仅有19.4％，准确率仍然高于80％，相关性指标和极大似然估计的各类误差均很大。因此，总相关估计的效果最好。

表4

由图6可知，在15个样本下，大部分情形下总相关估计的相对误差均最小。由表4可知，总相关估计的各类误差均远小于相关性指标和极大似然估计，准确率达到76.6％，远高于相关性指标和极大似然估计。

表5

由图7可知，在10个样本下，大部分情形下总相关估计的相对误差均最低。由表5可知，总相关估计的平均相对误差和最小相对误差均最小，最大相对误差略大于极大似然估计。考虑到总相关估计仅用10个样本，平均准确率达到68.9％，说明总相关估计的效果仍然不错，具有可靠性。

三种参数估计方法的平均相对误差、最小相对误差和最大相对误差与样本量之间的变化情况如图8～10所示。

由图8可知，三种参数估计方法的平均相对误差均随样本量减小而增大。不管样本数量是30、25、20、15或10，总相关估计的平均相对误差均远低于相关性指标和极大似然估计。样本量15时总相关估计的平均相对误差比样本量30时相关性指标和总相关估计的平均相对误差还小。与相关性指标相比，总相关估计大约改进了41.5％～46.2％；与极大似然估计相比，总相关估计大约改进了15.6％～41.2％。

由图9可知，不管样本数量是30、25、20、15或10，总相关估计的最小相对误差均最小。由图10可知，三种参数估计方法的最大相对误差均随样本量减小而增大，除样本量为10时总相关估计与极大似然估计的最大相对误差基本持平外，相关性指标和极大似然估计的最大相对误差均远大于总相关估计，说明小样本情景下相关性指标和极大似然估计具有很大的不确定性。

综上，实验结果表明本发明的参数估计方法在小样本情景下具有更大的可靠性和应用潜力：

(1)不管小样本数量是30、25、20、15或10，总相关估计均显著优于相关性指标和极大似然估计。

(2)根据不同小样本情形的平均相对误差计算结果，与相关性指标相比，总相关估计大约改进了41.5％～46.2％；与极大似然估计相比，总相关估计大约改进了15.6％～41.2％。

(3)当样本量处于15到30之间时，总相关估计计算参数的平均准确率为76.6％～85.5％；当样本量为10时，总相关估计的平均准确率达到68.9％，仍可获得一个较好的结果。

根据得到的最优copula函数构建水文变量的联合分布函数，由此计算联合重现期t1、同现重现期t2和条件概率p(x2≤x2|x1＞x1)等，计算公式如下：

其中，f1(x1)为二维随机变量(x1,x2)关于x1的边缘分布函数，f2(x2)二维随机变量(x1,x2)关于x2的边缘分布函数，c(f1(x1),f2(x2)；p)为frankcopula的分布函数，p为frankcopula函数的未知参数。(x1,x2)的取值范围用(x1,x2)来刻画，(x1,x2)为二维实变量。