一种基于二维码的物体空间位姿获取方法

本发明涉及物体姿态感知技术领域，主要涉及一种基于二维码的物体空间位姿获取方法。

背景技术：

随着近年来二维码技术的发展与普及，可以说人们在生活中已经离不开二维码，如二维码支付、二维码名片等。这类应用大多使用的是二维码携带文本信息的功能，但同时，二维码也可以提供精确的位姿信息。

目前大多对于物体位姿的解算依赖的是双目摄像头或深度摄像头等，不仅成本高昂，而且体积较大，不利于移动设备上的搭载。也有在物体上搭载惯性传感器来完成位姿检测，但这一方案同样面临成本高昂，传感器易损坏等问题。所以物体的位姿检测需要一种便捷且低成本的解决方案。

基于二维码的物体空间位姿获取系统在工业生产、物流运输、影视特效、展览、教育等领域有着广泛的应用前景，同时对于在便携设备和算力不充足的设备上实现物体的位姿解算有着重要意义。

技术实现要素：

发明目的：针对上述背景技术中存在的问题，本发明提供了一种基于二维码的物体空间位姿获取方法，实现了用一般的单目摄像头解算物体位姿的功能，成本低、易部署。该方法可以解算获得单个二维码的位姿，也可以通过在物体表面粘贴多个二维码来实现对物体全方位的位姿获取。

技术方案：为实现上述目的，本发明采用的技术方案为：

一种基于二维码的物体空间位姿获取方法，包括以下步骤：

步骤s1、基于单目摄像头获取目标的实时图像，输入至处理器；

步骤s2、处理器对实时图像进行二值化处理，并找出图像中所有的二维码，获取实时图像的二维码位置坐标信息；

步骤s3、对所述二维码位置坐标进行单应变换，获得二维码的单应变换矩阵；

步骤s4、基于所述单应变换矩阵获取二维码的欧拉角和空间位置；

步骤s5、记录各二维码的相对位置关系，将各二维码的欧拉角转换成轴角，融合各个二维码坐标系，并将融合后的坐标系对应到空间坐标系上；基于已识别的二维码当前位姿，获取融合后坐标系上的位姿，得到物体在空间坐标系下的位姿。

进一步地，所述步骤s3中获取二维码的单应变换矩阵具体步骤如下：

设定相机内参矩阵为单应变换矩阵

其中，fx和fy分别为相机在x和y方向上的焦距，cx和cy分别为相机中心与图像传感器中心在x和y方向上的偏移量；基于相机内参矩阵k和单应变换矩阵h，获得旋转矩阵和位置矩阵

相机投影矩阵表示为：p＝k[r|t]，空间点x通过投影矩阵变换为图像上的像素点x，投影关系表示为：x＝px；设定二维码所在平面为x-y平面，即z＝0，中心为坐标原点，则对于二维码平面：

将旋转矩阵r的第三列去掉可得：

其中r0，r1分别是r的第一列和第二列；则k[r0r1t]即为所述单应变换矩阵。

进一步地，所述步骤s4中获取二维码的欧拉角和空间位置具体步骤如下：

设定旋转矩阵计算四元数q＝(q0q1q2q3)如下：

由可得：

其中，(αβγ)代表二维码的欧拉角；使用atan2函数代替arctan函数表示如下：

设定其中λ为缩放比例，代表缩放后的单位二维码的角点，则

通过非单位化的单应变换矩阵得到旋转矩阵和r和位置矩阵t。

进一步地，所述步骤s5中，将各二维码的欧拉角转换为轴角具体步骤如下：

angle＝2*arccos(c1c2c3-s1s2s3)

x＝c1c2s3+s1s2c3

y＝s1c2c3+c1s2s3

z＝c1s2c3-s1c2s3

其中：

α、β、γ分别为偏航角、横滚角和俯仰角；x、y、z为轴角中轴向量的坐标；angle为轴角中的角度。

有益效果：

本发明提供的基于二维码的物体空间位姿获取方法实现了用一般的单目摄像头解算物体位姿的功能，成本低、易部署。该系统可以解算获得单个二维码的位姿，也可以通过在物体表面粘贴多个二维码来实现对物体全方位的位姿获取。

附图说明

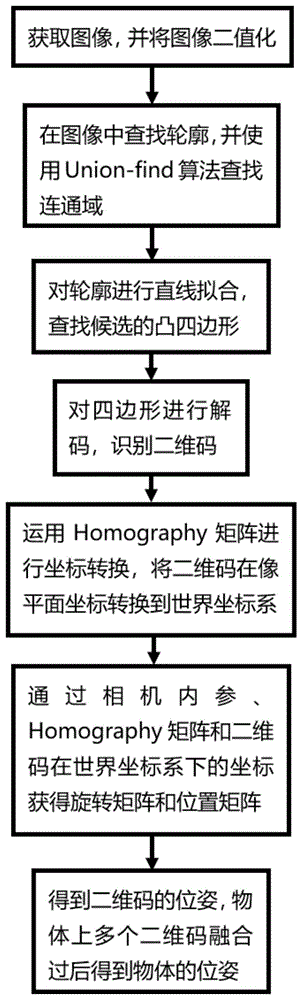
图1是本发明提供的基于二维码的物体空间位姿获取方法流程图；

图2是本发明实施例中使用的二维码与一般二维码对比图；

图3是本发明提供的单应变换原理示意图；

图4是本发明提供的物体表面二维码粘贴示意图与各二维码坐标系示意图。

具体实施方式

下面结合附图对本发明作更进一步的说明。

如图1所示的一种基于二维码的物体空间位姿获取方法，包括以下步骤：

步骤s1、基于单目摄像头获取目标的实时图像，输入至处理器。

步骤s2、处理器对实时图像进行二值化处理，对二值化后的图像进行阈值分割、连通域查找、直线拟合等图像处理算法，以此来找出图像中所有的二维码，并获得图像中二维码的坐标。本发明采用优化设计过的二维码样式，如图2所示，在保留表达文本信息能力的同时，比普通二维码图样更稀疏，以满足远距离识别的要求，并提高识别稳定性提升识别速度。

步骤s3、对所述二维码位置坐标进行单应变换，获得二维码的单应变换矩阵。具体如图3所示：

设定相机内参矩阵为单应变换矩阵

其中，fx和fy分别为相机在x和y方向上的焦距，cx和cy分别为相机中心与图像传感器中心在x和y方向上的偏移量；基于相机内参矩阵k和单应变换矩阵h，获得旋转矩阵和位置矩阵

相机投影矩阵表示为：p＝k[r|t]，空间点x通过投影矩阵变换为图像上的像素点x，投影关系表示为：x＝px；设定二维码所在平面为x-y平面，即z＝0，中心为坐标原点，则对于二维码平面：

将旋转矩阵r的第三列去掉可得：

其中r0，r1分别是r的第一列和第二列；则k[r0r1t]即为所述单应变换矩阵。

令k[λr0λr1t]＝k[r0′r1′t],可得如下等式：

fxr00′+cxr20′＝h00

fxr01′+cxr21′＝h01

fxtx+cxtz＝h12

fyr10′+cyr20′＝h10

fyr11′+cyr21′＝h11

fyty+cytz＝h12

r20′＝h20

r21′＝h21

tz＝h22

由此可解出[r0′r1′t]。然后对其进行单位化处理：

单位化后的r0，r1和r0′，r1′是一样的，t和t′是不同的。对于在相机图像上同一个二维码，t表示相机到r表示方向上实际大小二维码的距离，t′则表示相机到同一方向上实际大小为单位方形的二维码的距离。因为是对同一个二维码方形在t方向上的比例缩放，所以可以通过实际二维码的尺寸计算出相机到实际二维码的距离。若二维码的宽度为ω，那么相机到实际二维码的距离就为t＝ωt′。

步骤s4、基于所述单应变换矩阵获取二维码的欧拉角和空间位置。具体地，

设定旋转矩阵计算四元数q＝(q0q1q2q3)如下：

由可得：

其中，(αβγ)代表二维码的欧拉角；由于arctan的取值范围在-π/2和π/2之间，而α和γ的范围应当是360°，因此使用atan2函数代替arctan函数表示如下：

设定其中λ为缩放比例，代表缩放后的单位二维码的角点，则

通过非单位化的单应变换矩阵得到旋转矩阵和r和位置矩阵t。

步骤s5、记录各二维码的相对位置关系，将各二维码的欧拉角转换成轴角，融合各个二维码坐标系，并将融合后的坐标系对应到空间坐标系上；基于已识别的二维码当前位姿，获取融合后坐标系上的位姿，得到物体在空间坐标系下的位姿。

如图4所示，通过在一个物体上粘贴多个二维码，可以实现对这个物体全方位的位姿估计，避免二维码在摄像头视野中被遮挡。同时依据同一个物体上多个二维码的位置关系，可以由单个二维码的位姿信息得到该物体整体的位姿信息。考虑到多个二维码的欧拉角难以直接融合，多个二维码旋转时易出现混乱，须将欧拉角转换为轴角，具体步骤如下：

angle＝2*arccos(c1c2c3-s1s2s3)

x＝c1c2s3+s1s2c3

y＝s1c2c3+c1s2s3

z＝c1s2c3-s1c2s3

其中：

α、β、γ分别为偏航角、横滚角和俯仰角；x、y、z为轴角中轴向量的坐标；angle为轴角中的角度。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。