一种面向大规模打车平台的任务匹配公平方法

本发明属于计算机软件领域，涉及一种时空众包任务匹配方法，具体是一种面向大规模打车平台的任务匹配公平方法。

背景技术：

现有技术中，面向大规模打车平台的任务匹配方法大部分都侧重于提供理论性能保证；为了得到理论保证，现有方法通常会对司机和订单(任务)之间复杂的时序依赖做出简单的假设，导致在现实应用中无法达到预期效果；通过使用强化学习来提高打车平台的运行效率，不仅在模拟环境中实现了最佳性能并且已经成功部署到现实场景中。

针对公平性的匹配方法可分为两类：静态和动态。静态公平任务匹配中，工人和任务都是静态的，而在大规模打车场景中司机(工人)和订单(任务)都是动态出现，因此司机和订单之间的公平匹配属于动态公平匹配问题。在动态公平匹配领域，一些工作针对云计算和web请求分配问题研究的是如何实现多台服务器之间的负载均衡。然而，这些工作的优化目标是服务器(工人)为同样数量或价值的计算或web请求(任务)提供服务。这一公平目标不适用于打车场景，因为在打车场景中工人是司机，每个司机具有不同的工作时间以及时序依赖的工作范围。

技术实现要素：

针对上述问题，本发明考虑真实大规模打车场景的特性，基于强化学习兼顾公平和效率；提出了一种面向大规模打车平台的任务匹配公平方法，通过计算司机的收益率并通过公平性的量化指标进行验证，同时利用强化学习明确司机与订单匹配之间的时序依赖关系，学习可感知未来的匹配策略，并引导司机进入订单热区，达到了司机之间的收入公平性和平台总体效率双优化的效果。

所述的面向大规模打车平台的任务匹配公平方法，具体步骤如下：

步骤一、针对某城市，以固定时间频率将打车场景中空闲的在线司机和未服务的订单组成二分图；

二分图中的节点为司机和订单，司机和订单之间如果满足约束限制的空间距离，则两者之间存在一条边；

约束限制条件是指：在线空闲司机和未服务订单的空间直线距离小于阈值，阈值根据实际情况人为设定；

步骤二、初始化并更新当前时间窗内的二分图的边权；

具体过程为：

首先，将二分图的边权初始化为订单的价格；

订单价格为根据打车用户的出发地和目的地，打车平台自行计算的价格。

然后，根据初始的订单价格，利用价值函数更新所有二分图的边权；

更新公式为：

p为订单被取消的概率，pr为司机接受订单r的初始订单价格；y为折扣因子；τr为订单r完成需花费的时间；dr为订单r的目的地位置；为司机w的状态，包括司机当前位置和当前时间窗t；为状态价值函数；

步骤三、在更新完边权的二分图上，计算出每个在线司机对应的订单匹配。

具体过程为：

首先，利用bfs对二分图进行分解，对分解后的每个子图进行判断，如果子图只包含一个订单对应多个司机，或一个司机对应多个订单，直接从中选择权值最大的边作为匹配结果。

否则，针对每个子图，在km算法中使用dfs递归查找增广路；具体如下：

从司机w1出发，当访问到一个未匹配的订单r1，将该订单r1和司机w1匹配；否则，司机w1访问到一个已经和其他司机匹配的订单r2，则从该订单r2对应的匹配司机w2出发执行dfs查找增广路，判断司机w2是否在新的增广路上找到了新的匹配订单，如果没有，则司机w1继续访问其他订单；否则，司机w2在新的增广路上找到了新的匹配订单r3，按照km算法将司机w1和订单r2匹配，将司机w2和订单r3匹配；

为了满足公平性限制，对司机w1和订单r2匹配，司机w2和订单r3匹配后，判断司机w1和w2的收益率差距是否超过公平性限制；如果是，则放弃司机w1和订单r2匹配，保留w2和订单r2匹配；否则匹配成功。

司机收益率fw计算公式为：

其中，t表示一天，t表示一个时间窗，是二元指示器，如果司机w在线则如果司机从平台下线则表示司机在当前时间窗内的效率，如果司机和某个订单r匹配且订单没有被取消，则否则ξ^(t)是权重因子。

步骤四、对在线司机与对应订单的匹配结果进行学习，更新价值函数，并返回步骤二用于下一个时间窗的评估；

具体为：

首先，对每个匹配结果中的司机价值函数更新，计算公式为：

其中，β为学习率，δw的计算方式如下。

然后，根据同一个地理位置的多个司机共享价值函数，将价值函数简化为：

其中，l表示该城市所有可能打车的位置集合；w:lw是指在同一个地理位置的所有司机；δw简化为：

接着，将城市分为六边形网格和正方形网格，并找到各司机所在位置属于的六边形网格和正方形网格，得到两个价值函数h()和s()，选取司机所属网格附近网格的平均价值函数进行平滑，公式如下：

其中，dirh指定了六边形层用于光滑的有向偏移量，dirs指定了正方形层用于光滑的有向偏移量，h()是城市空间的六边形层对应的价值函数，s()是城市空间的正方形层对应的价值函数。

步骤五、根据更新的价值函数引导空闲的在线司机进入订单热区，避免在线学习的冷启动。

具体为：

laf按照引导策略将空闲的在线司机调度到附近的价值高的六边形网格所在区域；

引导策略为：对于每个空闲时间超过阈值的在线司机，分别计算各司机的收益率，并将收益率按从小到大排序，然后依次根据如下公式计算各司机被调往的六边形网格g。

其中，ah表示城市空间的所有六边形网格集合，dist表示司机被调往的格子和当前所在网格之间的距离。

本发明的优点在于：

1)、一种面向大规模打车平台的任务匹配公平方法，适应高度动态的交通，符合实际情况，方法时间效率高，适用于大规模的打车应用；

2)、一种面向大规模打车平台的任务匹配公平方法，使用在线强化学习建模司机和订单的匹配问题，在线学习可以快速捕捉当前供需时空分布的变化，并根据变化及时调整价值函数。

3)、一种面向大规模打车平台的任务匹配公平方法，在空间离散化方面，将城市空间划分为两层结构——六边形层和正方形层，六边形层用于捕捉与主干道形状类似的放射状径向模式，正方形层用于捕捉与经纬度平行的规则区域。

4)、一种面向大规模打车平台的任务匹配公平方法，为了避免价值函数的冷启动问题加入引导策略，调度司机到附近价值高的网格，实现了各司机的收益公平。

5)、一种面向大规模打车平台的任务匹配公平方法，将公平性检查嵌入到查找增广路过程中，没有增加额外的时间复杂度。

6)、一种面向大规模打车平台的任务匹配公平方法，考虑司机订单二分图的稀疏性对其进行分解，在子图上执行匹配，并且对于只有单个司机或者单个订单的二分图进行特判处理，可以极大地提高匹配速度。

附图说明

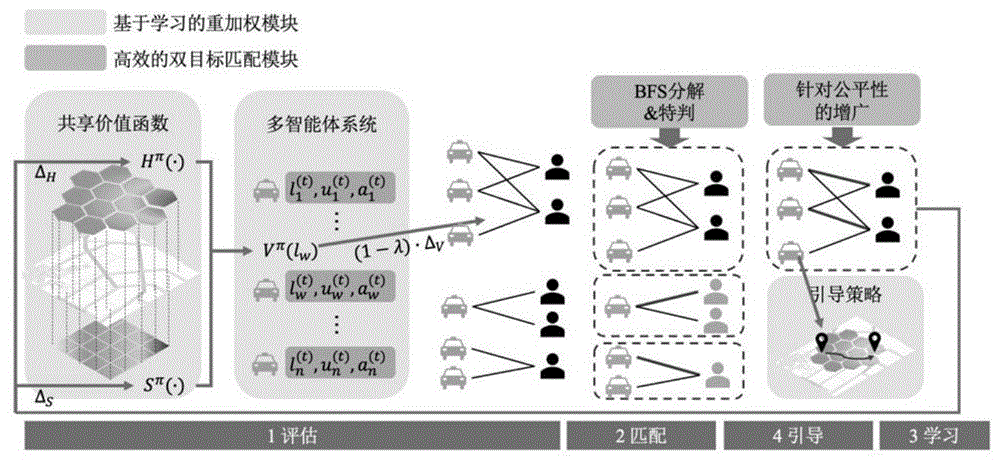
图1为本发明一种面向大规模打车平台的任务匹配公平方法的原理图；

图2为本发明一种面向大规模打车平台的任务匹配公平方法的流程图；

图3a为本发明实施例中17:00时的六边形网格对应的价值函数示意图；

图3b为本发明实施例中17:00时的正方形网格对应的价值函数示意图。

具体实施方式

下面将结合附图对本发明作进一步详细说明。

本发明一种面向大规模打车平台的任务匹配公平方法，实施平台是使用python构建的模拟器；通过模拟器加载订单数据，模拟司机和乘客的行为(即司机的上下线、调度司机的位置变化、空车的随机游走以及乘客拒单等)，以固定频率(如2s)调用laf(learningtoassignwithfairness)，每次调用时输入为当前时间窗(如2s)下空闲的司机和未服务的订单组成的二分图，laf依次执行评估、匹配、学习和引导四个步骤之后，向模拟器输出司机和订单的匹配结果。

如图1所示，评估是指将输入二分图的边权初始化为订单的(估计)价格，基于学习的重加权模块将根据价值函数更新边权，使得边权同时反映即时收益和未来收益；匹配是指高效的双目标匹配模块在考虑效率和公平的前提下，在调整完边权的二分图上计算出一个司机与订单的匹配。学习是指重加权模块将从匹配结果中学习，得到一个新的价值函数以用于下一个时间窗的评估步骤；引导是指根据新价值函数引导空闲司机进入订单热区(订单数量多的地区)，以避免在线学习的冷启动。

所述的基于学习的重加权模块应用在线强化学习来建模当前匹配对未来效率和公平的影响。高效的双目标匹配模块将公平性检查嵌入到查找增广路过程中，在满足公平性限制的同时最大化效率；效率被定义为打车平台上所有司机一天的总收入，是本模块的最大化优化目标。高效的双目标匹配模块在有权二分图的基础上执行带有限制条件的km算法求得司机订单匹配结果。

所述的面向大规模打车平台的任务匹配公平方法，如图2所示，具体步骤如下：

步骤一、针对某城市，以固定时间频率将打车场景中空闲的在线司机和未服务的订单组成二分图；

二分图中的节点为司机和订单，司机和订单之间如果满足约束限制的空间距离，则两者之间存在一条边；

约束限制条件是指：一个在线空闲司机和一个未服务订单的空间直线距离小于阈值(如小于3km)，阈值根据实际情况人为设定；

打车场景中，每个在线司机被认为是一个智能体，每个时间窗内，司机作为智能体可以采取两种动作——接受订单r或者保持空闲状态，对应的即时收益为订单价格pr和0。司机w的状态由他所在位置和时间窗t确定，基于学习的重加权模块的核心是司机遵从策略π得到的状态价值函数其中策略π的目标是优化效率(平台总收入，即所有司机收入的总和)和公平(司机群体收入公平性)。

步骤二、初始化并更新当前时间窗内的二分图的边权；

具体过程为：

首先，将二分图的边权初始化为订单的价格；

订单价格为根据打车用户的出发地和目的地，打车平台自行计算的价格。

然后，根据初始的订单价格，利用状态价值函数对输入二分图的每条边重新计算td(0)误差结合订单取消概率p作为权重：

权重的物理含义为司机w选择接受订单r相比留在原地可以多获得的期望收入。

更新公式为：

p为订单被取消的概率，pr为司机接受订单r的初始订单价格；y为折扣因子；τr为订单r完成需花费的时间；dr为订单r的目的地位置；为司机w的状态；为状态价值函数；

步骤三、在更新完边权的二分图上，计算出每个在线司机对应的订单匹配。

具体过程为：

首先，利用bfs对二分图进行分解，对分解后的每个子图进行特判，如果子图只包含一个订单对应多个司机，或一个司机对应多个订单，直接从中选择权值最大的边作为匹配结果，提高了匹配速度。否则，针对每个子图，在km算法中使用dfs递归查找增广路；具体如下：

从司机w1出发，当访问到一个未匹配的订单r1，将该订单r1和司机w1匹配；否则，司机w1访问到一个已经和其他司机匹配的订单r2，则从该订单r2对应的匹配司机w2出发执行dfs查找增广路，判断司机w2是否在新的增广路上找到了新的匹配订单，如果没有，则司机w1继续访问其他订单；否则，司机w2在新的增广路上找到了新的匹配订单r3，按照km算法将司机w1和订单r2匹配，将司机w2和订单r3匹配；

为了满足公平性限制，对司机w1和订单r2匹配，司机w2和订单r3匹配后执行公平性检查，判断司机w1和w2的收益率差距是否超过公平性限制；如果是，则放弃司机w1和订单r2匹配，保留w2和订单r2匹配；否则匹配成功。

司机收益率fw也称为时序加权分期收入，计算公式为：

其中，t表示一天，t表示一个时间窗(如2秒)，是二元指示器，如果司机w在线则如果司机从平台下线则表示司机在当前时间窗内的效率，如果司机和某个订单r匹配且订单没有被取消，则否则ξ^(t)是权重因子，laf将该权重设置为当前时间窗所在小时司机群体收入的中位数，用于平衡订单一天内在时空分布上的剧烈变化。

根据司机收益率，可以以熵的形式定义司机群体收入公平性的量化指标，进行验证；

如果f数值大则说明司机群体内收入差距很大，反之则说明司机群体内收入分布比较公平；如果每个司机的收益率是一样的，那么f＝0。

上述方法的时间复杂度为o(n²m)，其中m＝max(|w^(t)|,|r^(t)|),n＝min(|w^(t)|,|r^(t)|)，w^(t)是当前时间窗t的司机集合，r^(t)是当前时间窗t的订单集合。

步骤四、对在线司机与对应订单的匹配结果进行学习，更新价值函数，并返回步骤二用于下一个时间窗的评估；

价值函数根据匹配结果通过价值迭代的方法学习得到，具体为：

首先，对每个匹配结果中的司机价值函数更新，计算公式为：

其中，β为学习率，δw的计算方式如下。

在进行价值迭代的过程中司机的策略π也在隐式地改进以优化效率和公平目标，由于策略π不是所求，为了简化表示后面的写法中省略π。

然后，为了减少司机智能体需要探索的状态数量，实现有效的强化学习，除了对时空进行离散化(时间离散化是指将一天划分为若干等长的时间片如20分钟，空间离散化是指将一个城市划分为若干规则多边形，每个多边形称为一个网格)，还要1.对司机的状态简化，即只使用司机所在位置确定他的状态，2.多个司机共享同一个价值函数，因此价值函数更新的方式可以改写为：

其中，l表示该城市所有可能打车的位置集合；w:lw是指在同一个地理位置的所有司机；δw简化为：

接着，在空间离散化方面，laf将城市空间划分为两层结构——六边形网格层和正方形网格层，即城市被分为六边形网格和正方形网格，因此司机的位置使用这些网格来表示。找到各司机所在位置属于的六边形网格和正方形网格，得到两个价值函数h()和s()，从图3(a)中可以看出，六边形层可以显示出与主干道形状类似的放射状径向图案，而正方形层边界与经纬度平行，适用于规则区域，从图3(b)中可以看出一些繁忙区域。

laf对六边形层和正方形层对应的价值函数进行平滑，公式如下：

其中，dirh指定了六边形层用于光滑的有向偏移量，dirs指定了正方形层用于光滑的有向偏移量，h()是城市空间的六边形层对应的价值函数，s()是城市空间的正方形层对应的价值函数。

步骤五、根据更新的价值函数引导空闲的在线司机进入订单热区，避免在线学习的冷启动。

由于价值函数需要通过在线学习得到，所以在一开始价值函数会被初始化为0，导致二分图边权变成简单的即时收益pr，而缺少未来收益因此，laf会按照引导策略调度空闲的在线司机到附近的价值高的六边形网格所在区域。

引导策略具体为：对于每个空闲时间超过阈值(如5分钟)的在线司机，分别计算各司机的收益率，并将收益率按从小到大排序，然后依次根据如下公式计算各司机被调往的六边形网格g。

其中，ah表示城市空间的所有六边形网格集合，dist表示司机被调往的格子和当前所在网格之间的距离。

上述引导策略综合考虑了司机被调往的格子和当前所在格子的距离以及两个格子的价值差距，实现了调度司机到附近的价值高的六边形网格的效果。