基于相干累积功率与Kullback

基于相干累积功率与kullback
–
leibler散度的无网格线频估计方法
技术领域
1.本发明涉及数字信号处理领域，具体涉及一种基于相干累积功率与kullback
–
leibler散 度的无网格线频估计方法。


背景技术：

2.参数估计理论为通信、声呐和自动控制等领域发展奠定技术基础，其中频率估计作为重 要研究内容，受到学者广泛关注。数字信号处理中，通常将频率空间进行离散化处理，使用 某些网格点表示信号频率。离散化建模方法较为简单，易于分析处理，但频谱泄露降低了频 率分辨率且和主瓣峰值，降低频率估计结果的准确性，小样本数据尤甚。小样本单频信号映 射至离散频率空间时存在频谱泄露现象，导致线频展宽、分辨率降低，这制约着单频估计算 法准确性。同时，频谱泄露还造成信号谱峰下降，估计结果受噪声影响严重。尤其是在未知 概率分布噪声场景中，旁瓣易掩盖单频主瓣信息，以高斯白噪声为假设的单频估计算法的性 能，因谱间干扰而表现出不同程度恶化，而且估计误差与噪声概率分布有关。因此，在不同 概率分布场景下，准确、可靠地小样本频率信息是亟待解决的问题。


技术实现要素：

3.为提高小样本单频估计结果的准确度与稳定性，本发明一种基于相干累积功率与 kullback
–
leibler散度的无网格线频估计方法，有效的解决了上述的问题。利用相干累积功 率和kullback
–
leibler散度分别设计出无网格频率空间以及具有单调、强凸性质的代价函数， 然后，把单频估计问题转化为最大化无网格代价函数问题，从原理上消除了离散频率空间对 短时序列的约束，并提高了估计小样本单频信息的准确度。最后，利用kullback-leibler散度 设计出非线性放大映射，它能够在提升代价函数主瓣峰值锐度的同时保持旁瓣深零程度，从 而增强了在不同概率分布噪声条件下的稳定性。在未知概率分布噪声场景中，该方法可准确 且稳定地估计小样本信号的频率信息。
4.本发明的目的通过如下的技术方案来实现：
5.一种基于相干累积功率与kullback
–
leibler散度的无网格线频估计方法，包括以下过程：
6.步骤一，构建关于去均值的相干累积功率与频率的无网格空间；
7.步骤二，将去均值的相干累积功率的kullback
–
leibler散度在时域与频域上进行累积操作， 得到具有尖锐峰值与深零旁瓣性质的单调且强凸代价函数；求解代价函数的最大值，得到估 计频率。
8.进一步地，所述步骤一具体包括如下子步骤：
9.(1.1)构建傅里叶基函数
[0010][0011]
其中，为角频率的估计值；
[0012]
(1.2)将复指数线频信号x与傅里叶基函数h作hadamard乘积，得到相位差信号得到相位差信号
[0013]
其中，为差分频率，为幅值；ω为归一化角频率；φ为初始相位；
[0014]
(1.3)计算去均值的相干累积功率
[0015][0016]
式中，u为代表时间符号。
[0017]
进一步地，所述步骤二具体包括如下子步骤：
[0018]
(2.1)根据下式计算去均值的相干累积功率的kullback
–
leibler散度
[0019][0020]
其中，ε为正参考量，为相干累积功率的修正量；
[0021]
(2.2)将在时域t∈[0,t]进行累计操作
[0022][0023][0024]
其中，是关于的单调函数；
[0025]
(2.3)将进行频域累计操作，得到具有尖锐峰值与深零旁瓣性质的单调且强凸 代价函数
[0026][0027]
(2.4)使用adambelief算法确定的最大值，得到估计频率。
[0028]
进一步地，φ为初始相位，且独立同分布于区间[-π,π)。
[0029]
本发明针对小样本单频信号数据和未知概率分布噪声场景，设计了基于相干累积相位功 率和kullback
–
leibler散度的线频估计方法，提高了线频估计结果的准确性和稳
定性。本发明 与常规线频估计方法相比具有以下优点：
[0030]
(1)在证明功率与频率之间单调性的基础上，构造出关于相位差分功率与差分频率的无 网格代价函数，把单频估计问题转化为最大化无网格代价函数问题，从原理上消除了离散频 率空间对短时序列的约束，并提高了小样本单频估计结果的准确度。
[0031]
(2)利用kullback-leibler散度设计出非线性放大映射，它能够在提升代价函数主瓣峰 值锐度的同时保持旁瓣深零程度，从而增强了在不同概率分布噪声条件下的稳定性，可适用 于小样本数据的频率估计问题。
[0032]
(3)本发明的方法可在不同概率分布以及小样本数据场景下，准确、可靠地估计线频信 号的频率信息。
附图说明
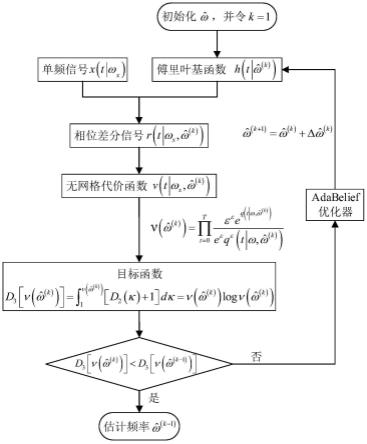
[0033]
图1为本发明的方法的流程图。
[0034]
图2为本发明实施例的图2为本发明实施例的随归一化差分频 率的变化趋势图。
[0035]
图3为本发明实施例的各方法在不同样本数量条件的估计结果：gsnr＝-5db条件下， 不同样本点对app-kld算法、广义加权线性预测算法和广义key估计算法的均方根误差的 影响；图(a)为在sαs分布噪声的特征指数α＝2，即白高斯噪声；图(b)为sαs分布噪声的特 征指数α＝1.6。
[0036]
图4为本发明实施例的各方法在不同广义信噪比条件的估计结果：样本点数n＝64条件 下，不同广义信噪比gsnr对app-kld算法、广义加权线性预测算法和广义key估计算法 的均方根误差的影响；图(a)为在sαs分布噪声的特征指数α＝2，即白高斯噪声；图(b)为sαs 分布噪声的特征指数α＝1.6。
具体实施方式
[0037]
下面根据附图和优选实施例详细描述本发明，本发明的目的和效果将变得更加明白，应 当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
[0038]
如图1所示，本发明的基于相干累积功率与kullback
–
leibler散度的无网格线频估计方 法，包括如下步骤：
[0039]
步骤一：构建关于去均值的相干累积功率与频率的无网格空间；
[0040]
复指数线频信号可定义为：
[0041]
x(t)＝ae
j(ωt+φ)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0042]
式中：
[0043]
为幅值；
[0044]
ω为归一化角频率；
[0045]
φ为初始相位且独立同分布于区间[-π,π)。
[0046]
在离散化频率空间内，式(1)所示的线频信号x通常由最接近其真值频率的傅里叶基函 数表示，即
[0047]
x＝ψ0a',
ꢀꢀꢀꢀꢀꢀꢀ
(2)
[0048]
式中：
[0049]
a'为傅里叶基函数ψ0的系数。
[0050]
若信号x实际频率不是频率空间的分辨率的整数倍，则该离散频率空间的任一频率点均 不能无失真地表示信号x的频率信息，ψ0也就无法作为准确表示信号x的傅里叶基函数。而 事实上，存在一个恰当的傅里叶基函数以及系数a可以无失真还原信号x，即x＝ψ1a。 离散频率空间的傅里叶基函数与可真实表示信号傅里叶基函数之间存在差异，即ψ0≠ψ1，称 之为基不匹配。
[0051]
为了从本质上解决基不匹配问题，本发明证明了去均值的相干累积功率是其正/负频率的 单调递减/增函数，并在此基础上提出信号x与傅里叶基函数所得差分信号的去均值功率函数 是差分频率绝对值的单调递减函数。于是，通过计算功率函数最大值的解，可以从本质上消 除基不匹配问题。
[0052]
相位差分是信号频谱估计的常用工具，它可视为信号与傅里叶基函数的hadamard乘积。 这里，根据式(1)的复指数线频信号设计如下傅里叶基函数
[0053][0054]
式中：
[0055]
为角频率的估计值。
[0056]
复指数线频信号x与傅里叶基函数h的hadamard乘积为相位差信号即
[0057][0058]
式中：
[0059]
为差分频率；为幅值；ω为归一化角频率；φ为初始相位；
[0060]
基于相位差分的频率估计方法大都对r做线性变换(如加权累积)或非线性变换(最大 似然)。由于信号x与傅里叶基函数具备相关性，而独立同分布噪声与傅里叶基函数不具备相 关性或仅某些短时片段内存在相关性，随样本量增加，信噪比也会随之增加。在样本量相对 较大和噪声能量较小时，这种基于相位累积的频率估计方法能够确保信号频谱估计的有效性。 然而，概率分布未知的噪声与傅里叶基函数h的相位差分累积可能导致能量激增，如具有瞬 态、宽频、高能特性脉冲噪声与傅里叶基函数的hadamard乘积严重偏离大部分数据，这些 野值点很容易遮盖相位差信号中有效数据的频谱信息。为了抑制概率分布未知的噪声对有效 相位差分信息的干扰，提出去均值的相干累积功率其表达式为
[0061][0062]
式中，*为共轭运算；为相位差信号r在前t时刻内的累积相位差；为累积相位差 的平均值；
[0063]
式(5)中，累积相位差的解析解为
[0064][0065]
累积相位差的平均值的解析解为
[0066][0067]
将式(6)和式(7)代入式(5)，可以得到去均值的相干累积功率v的解析解
[0068][0069]
不同于简单的相关累积方法，去均值的相干累积功率v通过计算前t时刻内功率与其均值 之差，能够抑制独立同分布噪声与傅里叶基函数的hadamard乘积带来的能量激增，一定程 度上提升有效频谱的信噪比。
[0070]
步骤二：设计去均值的相干累积功率的kullback
–
leibler散度，构造出凸函数。
[0071]
根据convex optimal第3章所述，相比熵、jensen-shannon散度等距离度量工具， kullback-leibler散度作为两个正向量的相对熵和线性函数之和，不仅可以测量概率向量之间 差异，还可以扩展至正向量。并且作为凸函数，kullback-leibler散度经过保凸运算后，可以 提升对多种独立同分布噪声扰动不敏感的特性。因此，在去均值的相干累积功率v基础上， 利用kullback-leibler散度构造凸函数，该算法以度量功率向量v与参考向量p差异为基础， 实现小样本及低信噪比条件下准确地且稳定地估计信号频率。
[0072]
已知在t时刻，相对于参考量p(t)》0的kullback-leibler散度可以表示为
[0073][0074]
可以看做是相对熵与线性函数之和，因此是关于和 p(t)的凸函数。kullback-leibler散度总是非负的，当且仅当时， [0075]
去均值的相干累积功率在的过程中，是逐渐递减。此时，我
们选 取的一种极限情况，即
[0076][0077]
作为式(9)中的参考量来度量随差分频率的变化情况。然而，考虑到kullback-leibler 散度是度量两个正向量之间差异的量值，参考量p(t)取零不满足kullback-leibler散度的变量 定义域要求。故而修正参考量相应地，于是，重新整理 式(9)可得
[0078][0079]
根据kullback-leibler散度定义，若时，与p(t)具有相同值，即
[0080][0081]
式(12)表明在与p(t)的kullback-leibler散度有最小值，即
[0082]
步骤三，通过在时域与频域进行非线性累积放大映射，将kullback-leibler散度构造的 凸函数转变为尖锐峰值、深零旁瓣的强凸函数。
[0083]
为进一步提高未知概率分布噪声条件下的鲁棒性，式(11)可通过非线性累积放 大变换以实现尖锐峰值、深零旁瓣的强凸函数。在小样本或未知概率分布的强噪声情况时， 使用该强凸函数作为代价函数，可以显著提升频率估计的准确性和稳定性。
[0084]
就时域而言，在采样时间内的任意时刻，即t∈[0,t]，均是关于的单调函数， 同时也是关于的凸函数。根据保凸运算中非负加权求和准则，对式(11)在t∈[0,t]区 间内做积分，于是有
[0085][0086]
该式的凸性与单调性均与式(11)保持一致。
[0087]
定义
[0088][0089]
根据连续函数的连乘定义，式(14)可以重新整理为
[0090][0091]
将式(15)所示的连乘关系代入式(13)，可以将其化简为
[0092][0093]
式中，是关于的单调函数，且log也是单调函数，所以与一致，是关于 的凸函数。此外，可以视为复合函数的函数，故有
[0094]
按照上述时域积分的保凸原理，由于是关于差分频率单调递增的，在频域上 对从到当前差分频率值做积分，会进一步增强kullback-leibler散度的凸 性。但是考虑到差分频率作为积分函数自变量难以得到解析解，因此，取差分频率的单 调函数作为积分变量。得益于与的单调性，对做积分运算，相对于p(t)的kullback-leibler散度会以非线性方式增加。
[0095]
由于是偶函数，不失一般性地选取计算在区间的积分函数， 即从最大频率差分到当前频率差分值的累计量。将式(8)代入式(15)，可以得到 的积分下限
[0096][0097]
因此，的变上限积分为
[0098][0099]
其中，被积函数中引入“1”是为保证得到简约的解析解，同时保证不会影响最终的解 convex optimal第3章表明，是关于的凸函数。
[0100]
无噪声条件下，和随的变换曲线如图2所示。在区间与 上，和均为的严格单调函数，且二者最大值均在处。 相比于表现出尖锐峰值，具有更强凸性。另外，的深零旁瓣也 会表现出稳定地抗白噪声能力，较更能使用概率分布未知的白噪声。
[0101]
步骤四：使用adambelief算法确定收敛值。
[0102]
每次迭代过程中计算相位差分累积r(ω
x
,ω)、功率v(ω
x
,ω)以及无网格代价函数d3[ν(ω
x
,ω)]，同时根据当前迭代与上次迭代的无网格代价函数使傅里叶基函数的频率值ω
x
不断朝最大化d3[ν(ω
x
,ω)]的方向移动，直至估计频率ω
x
与信号频率ω的差值在误差范围之 内，此时所得的频率值ω
x
即为估计频率。
[0103]
图3分析了不同样本数量对基于kullback
–
leibler散度的累积相位差分功率的频率估计算 法以及经典算法的影响。仿真中，分别设置sαs分布噪声的特征指数α＝2和α＝1.6，在 gsnr＝-5db条件下，信号样本n每隔10从30采样点增加到100采样点。经过1000次 monte-carlo仿真实验，均方根误差的平均值随样本点数变化曲线如图2所示。从图2(b)可
以 看出，app-kld算法对sαs分布噪声中的野值点不敏感，其估计准确度远高于广义加权线 性预测算法和广义key估计算法。在gsnr＝-5db条件下，样本点n≥60时，app-kld算 法几乎可以达到克拉美罗下界。样本点n《60时，相对于广义加权线性预测算法和广义key 估计算法，app-kld算法依然与克拉美罗下界保持较近距离。因此，可以说明app-kld算 法更加适用于针对小样本的频率估计场景。
[0104]
图3分析不同信噪比对基于kullback
–
leibler散度的累积相位差分功率的频率估计算法以 及经典算法的影响。仿真中，分别设置sαs分布噪声的特征指数α＝2和α＝1.6，在样本点 n＝64条件下，广义信噪比gsnr每隔3db从-30db增加到30db。经过1000次monte-carlo 仿真实验，均方根误差的平均值随广义信噪比变化曲线如图3所示。从图3可以看出，无论 在白高斯噪声还是sαs分布噪声场景下，app-mls算法均具有较高的稳定性，在广义信噪 比gsnr≥-9db时，均可达到克拉美罗下界。然而，分析图3-4(a)可知，在白高斯噪声环境 中，广义加权线性预测算法
[43]
、广义key估计算法
[42]
分别在gsnr大于-3db、6db时，可以 达到克拉美罗下界；在α＝1.6的重拖尾环境中，在gsnr∈[-30,30]db二者精度相对较差， 距离克拉美罗下界有一定距离。此外，对比图3-4(a)和(b)，在gsnr∈[-20,30]db范围内，由 于广义加权线性预测算法和广义key估计算法在白高斯噪声环境中估计频率的准确性优于重 拖尾效应环境。因此，可以说明app-mls算法在高信噪比和较低场景均可保证频率估计的 准确性。
[0105]
本领域普通技术人员可以理解，以上所述仅为发明的优选实例而已，并不用于限制发明， 尽管参照前述实例对发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前 述各实例记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在发明的精 神和原则之内，所做的修改、等同替换等均应包含在发明的保护范围之内。