基于混合有限元空间求解板弯曲问题的方法

本技术涉及弹性力学，具体而言，涉及一种基于混合有限元空间求解板弯曲问题的方法。

背景技术：

1、薄板弯曲是工程中常见的力学现象，其通常会涉及到结构设计、制造工艺、材料性能等多个方面，例如飞机机翼、汽车车身钣金件、建筑的金属屋顶等都是典型的薄板结构。在设计这些结构时，需要考虑薄板件的弯曲性能，确保其在外载作用下不会过度变形或破坏。同时，制造薄板结构通常需要通过折弯、冲压成型等工艺获所需形状。因此，了解薄板的弯曲行为对于选择合适的制造工艺、决定加工参数以及预测成品质量具有重要意义。

2、通常，薄板弯曲可以简化成关于挠度和荷载的薄板弯曲方程，同时由于实际工程结构中的工程部件或者机械部件的几何形状不规则，相应地受力情况也会变得复杂，若采用传统有限元方法进行分析，若网格不够细致，则可能无法准确捕捉局部应力集中和变形情况，但过于细致的网格又会增加计算成本。

3、针对上述的问题，目前尚未提出有效的解决方案。

技术实现思路

1、本技术实施例提供了一种基于混合有限元空间求解板弯曲问题的方法，以至少解决相关技术中在分析薄板弯曲过程中，采用传统有限元法求解对应的偏微分方程无法在网格数量较少的情况下提升计算精度的技术问题。

2、根据本技术实施例的一个方面，提供了一种基于混合有限元空间求解板弯曲问题的方法，包括如下求解步骤：

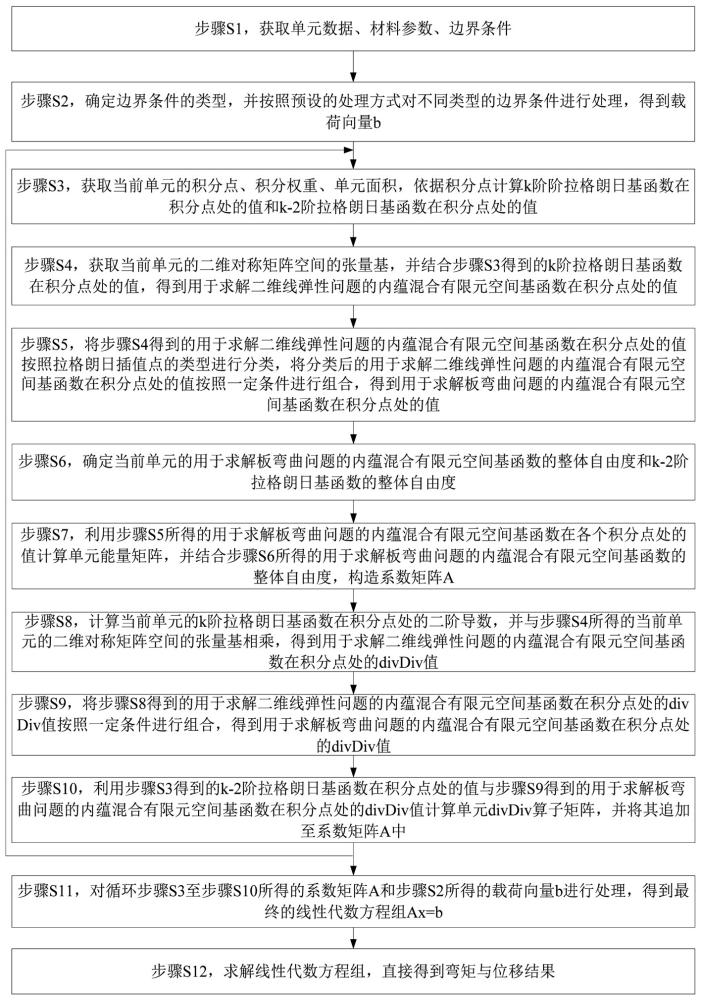
3、步骤s1，获取单元数据、材料参数、边界条件，其中，单元数据包括：单元形状、节点坐标、单元数量、单元维度，边界条件包括：应力约束、弯矩约束、位移约束、转角约束，材料参数包括：板的厚度、杨氏模量、泊松比、密度；

4、步骤s2，确定边界条件的类型，并按照预设的处理方式对不同类型的边界条件进行处理，得到载荷向量b；

5、步骤s3，获取当前单元的积分点、积分权重、单元面积，依据积分点计算k阶拉格朗日基函数在积分点处的值和k-2阶拉格朗日基函数在积分点处的值，其中，k为大于等于3的整数；

6、步骤s4，获取当前单元的二维对称矩阵空间的张量基，并结合步骤s3得到的k阶拉格朗日基函数在积分点处的值，得到用于求解二维线弹性问题的内蕴混合有限元空间基函数在积分点处的值；

7、步骤s5，将步骤s4得到的用于求解二维线弹性问题的内蕴混合有限元空间基函数在积分点处的值按照拉格朗日插值点的类型进行分类，将分类后的用于求解二维线弹性问题的内蕴混合有限元空间基函数在积分点处的值按照一定条件进行组合，得到用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的值；

8、步骤s6，确定当前单元的用于求解板弯曲问题的内蕴混合有限元空间基函数的整体自由度和k-2阶拉格朗日基函数的整体自由度；

9、步骤s7，利用步骤s5所得的用于求解板弯曲问题的内蕴混合有限元空间基函数在各个积分点处的值计算单元能量矩阵，并结合步骤s6所得的用于求解板弯曲问题的内蕴混合有限元空间基函数的整体自由度，构造系数矩阵a；

10、步骤s8，计算当前单元的k阶拉格朗日基函数在积分点处的二阶导数，并与步骤s4所得的当前单元的二维对称矩阵空间的张量基相乘，得到用于求解二维线弹性问题的内蕴混合有限元空间基函数在积分点处的divdiv值；

11、步骤s9，将步骤s8得到的用于求解二维线弹性问题的内蕴混合有限元空间基函数在积分点处的divdiv值按照一定条件进行组合，得到用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的divdiv值；

12、步骤s10，利用步骤s3得到的k-2阶拉格朗日基函数在积分点处的值与步骤s9得到的用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的divdiv值计算单元divdiv算子矩阵，并将其追加至系数矩阵a中；

13、步骤s11，对循环步骤s3至步骤s10所得的系数矩阵a和步骤s2所得的载荷向量b进行处理，得到最终的线性代数方程组ax=b；

14、步骤s12，求解线性代数方程组ax=b，直接得到弯矩与位移结果。

15、可选地，上述步骤s2包括如下步骤：

16、步骤s21，确定边界条件的类型；

17、步骤s22，在边界条件的类型为体力时，调用位移的测试函数空间，并将位移的测试函数空间与体力的积分结果加载到载荷向量b中；

18、步骤s23，在边界条件的类型为应力和/或弯矩时，调用最小二乘法对应力约束和/或弯矩约束进行处理；

19、步骤s24，在边界条件的类型为位移约束和/或转角约束时，调用弯矩的测试函数空间，并将弯矩的测试空间与位移约束和/或转角约束的积分结果加载至载荷向量b中。

20、可选地，上述步骤s4包括如下步骤：

21、步骤s41，确定当前单元上各个拉格朗日插值点的类型，其中，拉格朗日插值点的类型包括：单元顶点、单元内部点、边内部点；

22、步骤s42，根据拉格朗日插值点的类型确定二维对称矩阵空间的张量基，其中，在拉格朗日插值点的类型为单元顶点和单元内部点时，获取二阶对称张量空间的标准基；在拉格朗日插值点的类型为边内部点时，获取当前单元的三条单元边各自的一个单位切向向量和一个单位法向向量，并利用每条边的一个单位切向向量和一个单位法向向量计算该单元边的边基；

23、步骤s43，将二维对称矩阵空间的张量基与步骤s3所得的k阶拉格朗日基函数在积分点处的值结合，得到用于求解二维线弹性问题的内蕴混合有限元空间基函数在积分点处的值。

24、可选地，上述步骤s5包括如下步骤：

25、步骤s51，在拉格朗日插值点的类型为边内部点时，判断用于求解二维线弹性问题的内蕴混合有限元空间基函数是否由纯切向向量组成，若是则确定该用于求解二维线弹性问题的内蕴混合有限元空间基函数属于第一类基函数，否则属于第二类基函数；

26、步骤s52，在拉格朗日插值点的类型为单元内部点时，确定用于求解二维线弹性问题的内蕴混合有限元空间基函数属于第一类基函数；

27、步骤s53，在拉格朗日插值点的类型为单元顶点时，确定用于求解二维线弹性问题的内蕴混合有限元空间基函数属于第三类基函数；

28、步骤s54，将上述步骤s51至步骤s53所得的各类基函数按照一定条件进行组合，得到用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的值。

29、可选地，所述步骤s54包括如下步骤：

30、步骤s541，构造系数矩阵m，并利用系数矩阵m将步骤s51和步骤s52所得的第一类基函数进行组合，得到第一组用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的值；

31、步骤s542，构造系数矩阵n，并利用系数矩阵n将步骤s51所得的第二类基函数和步骤s541所得的第一组用于求解板弯曲问题的内蕴混合有限元空间基函数进行组合，得到第二组用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的值；

32、步骤s543，构造系数矩阵p，并利用系数矩阵p将步骤s53所得的第三类基函数和步骤s541所得的第一组用于求解板弯曲问题的内蕴混合有限元空间基函数进行组合，得到第三组用于求解板弯曲问题的内蕴混合有限元空间基函数在积分点处的值。

33、在本技术实施例中，通过对用于求解二维线弹性问题的内蕴混合有限元空间基函数进行分类并重新组合，以得到用于求解板弯曲问题的内蕴混合有限元空间基函数，利用该基函数在求解板弯曲问题时，其可以采用较少数量的网格上实现高精度的位移和弯矩结果，以解决了相关技术在分析薄板弯曲问题时，采用传统有限元法求解对应的偏微分方程无法在网格数量较少的情况下提升计算精度的技术问题。