一种保证时域逐点最大重构误差的模拟信号采样与重构的方法与流程

本发明涉及信号采样
技术领域：
，特别涉及一种保证时域逐点最大重构误差的模拟信号采样与重构的方法。
背景技术：
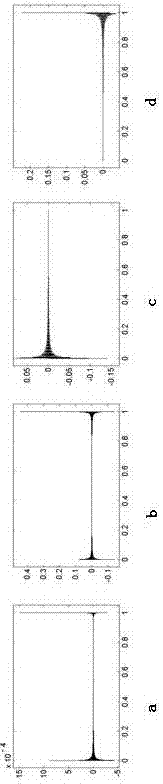
：在这个数字时代，把一个模拟信号先转换成数字信号再进行处理或存储等工作几乎成了一个标准过程。在这一转换过程中信号采样是基本的一个步骤。到目前为止用来确定采样率的基本理论是经典的针对带限信号的香农采样理论(例如文献[1],[2])。该理论的核心内容可以描述如下：对任意一个带宽为w的信号x(t)，如果采样率fs至少为2w，那么x(t)就可以由其采样点和sinc函数完美地重构出来。在进行采样器设计时香农理论可以看成一个基于频域的工具，因为其分析基础是基于信号的频谱。在过去几十年中沿着这一思路的跟进工作有许多(例如文献[1],[3]–[6])。针对某些类特殊信号的采样方法也被提出(例如文献[7]–[10])。香农框架虽然在理论上简洁漂亮，在实际设计采样器的过程中却可能带来不便或困难。首先，所有需要处理的实际模拟信号在时间上都是有限的，那么这些信号就必然是非带限信号[11]。所以任何频谱的截断就必然带来采样后的信号频谱混叠现象，从而产生误差。实际上，通常以下四种误差都需要考虑：频谱混叠误差，幅度误差，截断误差，以及时间抖动误差，如文献[12],[13]。这些误差分析也被用在小波分析上，如文献[14]。傅立叶分析中涉及到的著名的gibbs现象可能产生较大的瞬时误差，如文献[15]。随着高速dsp的应用越来越广，人们经常希望在保证时域逐点(pointwise)重构误差的前提下采样尽量少的数据点。香农理论在这方面没有提供什么支持。虽然有方法被提出来用于在保证重构误差的前提下尽量减少采样点的个数(例如文献[16])，目前还是缺乏适用于工程应用的简单有效的方法。在一些应用场合，我们并不能提前得到信号的频谱信息，也就不能直接应用香农理论了。并且，重构模拟信号的电路常常使用常数或线性插值，如文献[17]，但是在香农理论中用于插值的sinc函数在实际中是不能完全得到的。虽然香农理论中用到的能量稳定性在推导中方便使用，但是在工程实践中逐点(pointwise)的稳定性是更常期望的，尤其在研究信号瞬态特征的时候，如文献[3]。技术实现要素：本发明提出一种保证时域逐点最大重构误差的模拟信号采样与重构的方法，是一个纯粹基于时域的方法，用以在保证逐点最大重构误差的前提下进行有效的均匀采样。本发明所采用的技术方案为：一种保证时域逐点最大重构误差的模拟信号采样与重构的方法，待采样模拟信号x(t经过若干次模拟一阶微分电路后，对输出信号通过模拟电路求得其幅值的最大值，用以计算采样周期t，并以该采样周期t对延时后的待采样模拟信号x(t)进行采样，在重构时，利用拉格朗日插值多项式将各个采样值组成一个分段多项式来近似待采样连续模拟信号x(t)。进一步的:所述采样周期t的计算方法：式中：ε为最大允许重构误差，单位与待采样模拟信号x(t)的单位一致；k为重构多项式的最高阶数，k≥1，(k+1)！是k+1的阶乘；ηk+1为待采样连续模拟信号x(t)的k+1阶导数幅值的最大值。利用所述采样周期t进行采样，信号重构方法：式中：k为重构多项式的最高阶数，k≥1；整数m的取值范围是：n-k+1≤m≤n；li(t)是拉格朗日插值基函数其中ti＝it，tj＝jt；不需要对模拟信号的各阶导数进行采样，只利用待采样模拟信号的采样点；在重构每一个采样周期[nt,(n+1)t]上的信号内容时，利用包括采样点x(nt)和x((n+1)t)在内的k+1个连续采样点进行信号重构。与传统的香农采样理论相比，本发明的有益效果：1)易于分析与实现。本文提出的方法允许采样器的设计完全在时域进行。如果信号最大的变化率(x'(t)，x”(t)等)已知，可以很容易地计算出有效的采样周期。如果不知，如图3所示，可以由电路自动获得。但是在香农采样理论中，信号带宽无法很容易地通过模拟电路估计得到。2)保证每一个点的重构误差精度。在经典的香农采样理论中，这个通常在实践中所需要的功能几乎是缺失的。但是在本文所提出的方法中，可以设计保证时域每个点的最大重构误差。如具体实施部分论述所示，本发明重构误差范围很严谨。但是在香农采样理论中时域重构误差范围很难被估计，而且可能随着信号的变化而变化较大。3)适用于非带限可导模拟信号。所有的物理信号都是时间有限的，因此它们必然是非带限信号。所以在香农采样理论的实际应用中总是涉及到近似，而且也很难去分析每个点的时域重构误差。相比之下，本发明所提出的方法能够很容易地处理非带限模拟信号，并且重构误差可控。4)适用于未知特征的采样信号。在经典的香农采样理论中，在采样之前我们需要知道信号的带宽。但本发明提出的方法的实现结构不需要采样信号的任何信息，因为相关参数都可以在采样电路中得到。附图说明图1中a、b、c、d依次为本发明采用的四种待采样模拟信号x(t)示意图；图2中a、b、c、d依次为四种待采样连续模拟信号经过香农理论进行采样后的重构误差仿真结果示意图；图3为本发明的电路原理图，其中延时td与计算t的时间相当；图4中a、b、c、d依次为本发明的四种待采样连续模拟信号x(t)经过采样后的重构误差仿真结果示意图(k＝1)；图5中a、b、c、d依次为本发明的四种待采样连续模拟信号x(t)经过采样后的重构误差仿真结果示意图(k＝2)；图6中a、b、c、d依次为本发明的四种待采样连续模拟信号x(t)经过采样后的重构误差仿真结果示意图(k＝3)；图7中a、b、c、d依次为本发明的四种待采样连续模拟信号x(t)经过采样后的重构误差仿真结果示意图(k＝4)。具体实施方式下面结合附图对本发明及其效果进一步说明。我们先简单回顾香农采样理论。给定一个带宽为w的待采样模拟信号x(t)，先定义一个采样冲击序列信号其中采样周期t在下面确定，从而保证完美重构。s(t)的频谱可以写成其中采样率fs＝1/t。然后得到的采样序列就是xs(t)的频谱然后就可以写成其中*是卷积运算。公式(4)告诉我们为了得到完美重构，我们需要以下两个条件：1)fs≥2w(5)2)将xs(t)通过一个理想低通滤波器th(t)其中并且w＜fc＜fs-w(7)满足以上两个条件将使得重构信号xr(t)与x(t)具有相同的频谱。那么我们就得到在l2范数下xr(t)＝x(t)。滤波器的时域冲击响应h(t)是h(t)＝2fcsinc(2fct)(8)所以，利用公式(3)和(8)，xr(t)的解析表达式就是公式(9)是利用x(t)的采样点进行重构的公式。我们将以上的香农采样与重构方法归纳为算法af。在图1中我们列出四个测试信号，并且将算法af的重构效果列在图2中。图1中的四个信号全部定义在[0,1]区间上，并且依次为如下形式：x1(t)＝sin(2πt)(10)x2(t)＝cos(2πt)(11)x4(t)＝etsin(40πt2)(13)为了有效地采样(采集尽可能少的数据点)，我们希望在保证期望的精度的前提下使用尽可能大的采样周期t。第一个困难就是估计信号的带宽w。即使有了信号的表达式，我们通常在艰苦的推导后才得到如下的频谱：其中是1[0,1](t)的频谱。本质上与相同，而且对于和我们很难得到解析式注意这四个信号中没有一个的带宽w是有限的。所以我们就把带宽w定义为频谱从此以后衰减的足够小的频率点，即对于所有f>w，本文中我们固定εf＝10-3。然后我们就可以得到信号xk(t)的带宽wk如下：w3＝160w4＝138对于信号x3(t)和x4(t)，我们做了30000个点的过采样，然后使用fft得到其带宽w。为了满足公式(5)和(7)，我们选择fs＝2.1w以及fc＝fs/2。现在我们可以根据公式(9)进行信号采样与重构。但是在这之前，我们并不能对逐点的重构误差有什么保证，因为香农理论是通过l2范数建立起来的，或者如文献[3]描述的，香农理论只保证能量稳定性。如何将频域的误差上界转化为时域的误差还是一个尚未解决的问题。事实上，在4g和5g通信中广为研究的峰均功率比(papr)问题中这是一个核心难点(例如文献[18])。图2中显示的结果也部分展示了这个误差估计问题的复杂程度。我们看到对于信号x1(t)，最大重构误差在10-4数量级，低于10-3；但是对于本质上一样，拥有同样带宽和采样周期的信号x2(t)，重构误差可以高达约0.4。这是因为gibbs现象。信号x3(t)和x4(t)的重构误差在0.05和0.2的数量级。在本发明中我们提出一个基于时域的方法来回答如下问题：给定一个有限长度的待采样连续模拟信号x(t)以及一个最大的逐点重构误差上界ε，如何有效地对x(t)进行均匀采样，使得最大的逐点重构误差不超过ε？为此，本发明采用的方法是：将待采样模拟信号x(t)经过若干次模拟一阶微分电路后，对输出信号通过模拟电路求得其幅值的最大值(如文献[21])，用以计算采样周期t，并以该采样周期t对延时后的待采样连续模拟信号x(t)进行采样，在重构时，利用拉格朗日插值多项式将各个采样值组成一个分段多项式来近似待采样连续模拟信号x(t)。下面通过具体的实施例对上述方法进行验证说明。一种保证时域逐点最大重构误差的模拟信号采样与重构的方法，待采样连续模拟信号x(t)经过若干次一阶微分电路后，对输出信号通过模拟电路求得其幅值的最大值，用以计算采样周期并以该采样周期t对延时后的待采样连续模拟信号x(t)进行采样，在重构时，利用拉格朗日插值多项式将各个采样值组成一个分段多项式来近似待采样模拟信号x(t)。式中：ε为最大允许重构误差，单位与待采样连续模拟信号x(t)的单位一致；k为重构多项式的最高阶数，k≥1，(k+1)！是k+1的阶乘；ηk+1为待采样连续模拟信号x(t)的k+1阶导数幅值的最大值。利用所述采样周期t进行采样，信号重构方法：式中：k为重构多项式的最高阶数，k≥1；整数m的取值范围是：n-k+1≤m≤n；li(t)是拉格朗日插值基函数其中ti＝it，tj＝jt。不需要对模拟信号的各阶导数进行采样，只利用待采样模拟信号的采样点。在重构每一个采样周期[nt,(n+1)t]上的信号内容时，利用包括采样点x(nt)和x((n+1)t)在内的k+1个连续采样点进行信号重构。依据香农理论进行信号的采样与重构并不能对逐点的重构误差有什么保证，如附图2所示，不同信号的最大重构误差差别很大，有的重构误差在10-3数量级，有的在0.01数量级，还有的在0.1数量级，这显示了香农理论下误差估计问题的复杂程度。本发明能够使得最大信号重构误差完全满足设计要求，如附图4至附图7所示，本发明的重构方法在不同的k值下的重构误差均小于设计要求的10-3。不但如此，如表i所示，本发明采样周期与香农采样周期在同一个数量级或者更大，附图2显示香农采样后的最大重构误差达到0.4，远远高于本发明的0.001，也就是说，与香农框架相比，采用本发明的方法，可以在采样点数相当或更少的情况下，使得重构误差更小。表i四个测试信号由不同算法得到的采样周期talg.t1t2t3t4香农理论0.001496000.001496000.002976190.00345066本发明k＝10.014235250.014235250.011283790.00021787本发明k＝20.028920370.028920370.020583580.00051808本发明k＝30.041762030.041762030.024152830.00081923本发明k＝40.052074650.052074650.029059290.00106607一，证明如下：在采样区间[nt,(n+k)t]上存在k+1个采样点。利用k阶阶拉格朗日插值多项式,能得到重构模拟信号xr(t)形式如下(如文献[19])其中li(t)是拉格朗日插值基函数，其中ti＝(n+i-1)t，tj＝(n+j-1)t。重构误差由拉格朗日插值余项得到(如文献[19])那么在(19)式中我们使用了均值不等式(如文献[20])。如果k+1是一个奇数,我们有对和一个单独的采样点。一对采样点之间的最大距离是kt,重构点和这个单独的采样点之间的最大距离是因此我们可以很容易地得到如果k+1是一个偶数,我们有对采样点。类似地，我们能得到那么重构误差可以被界定为在(16)式中用了采样点x(nt)，x((n+1)t)，...，x((n+k)t)来重构xr(t)在区间[nt,(n+1)t]上的内容。类似的证明过程同样可以证明，如果采用任意包括x(nt)和x((n+1)t)在内的k+1个连续采样点来重构xr(t)在区间[nt,(n+1)t]上的内容，结论(22)式依然成立。二，具体实现算法0)确定重构多项式的参数k1)输入x(t)，t∈[0,1]，和时域逐点最大误差允许值ε2)估计3)设置采样间隔4)获取采样点x(nt)，5)利用公式(16)和(17)得到重构信号xr(t)。以下为本发明中所涉及的现有文献：[1]abdulj.jerri,“theshannonsamplingtheorem—itsvariousextensionsandapplications:atutorialreview,”proceedingsoftheieee,vol.65,no.11,pp.1565–1596,1977.[2]johng.proakisanddimitrisg.manolakis,digitalsignalprocessing:principles,algorithms,andapplications,4thed.,prentice-hall,2006.[3]p.p.vaidyanathan,“generalizationsofthesamplingtheorem:sevendecadesafternyquist,”ieeetransactionsoncircuitsandsystemsi:fundamentaltheoryandapplications,vol.48,no.9,pp.1094–1109,2001.[4]ahmedizayed,advancesinshannon’ssamplingtheory,crcpress,1993.[5]robertjiimarks,advancedtopicsinshannonsamplingandinterpolationtheory,springerscience&businessmedia,2012.[6]michaelunser,“sampling—50yearsaftershannon,”proceedingsoftheieee,vol.88,no.4,pp.569–587,2000.[7]rodneygvaughan,neillscott,anddrodwhite,“thetheoryofbandpasssampling,”ieeetransactionsonsignalprocessing,vol.39,no.9,pp.1973–1984,1991.[8]raymondboute,“thegeometryofbandpasssampling:asimpleandsafeapproach[lecturenotes],”ieeesignalprocessingmagazine,vol.29,no.4,pp.90–96,2012.[9]jasondmcewen,gillespuy,jean-philippethiran,pierrevandergheynst,dimitrivandeville,andyveswiaux,“sparsesignalreconstructiononthesphere:implicationsofanewsamplingtheorem,”ieeetransactionsonimageprocessing,vol.22,no.6,pp.2275–2285,2013.[10]hiromiuedaandtoshinoritsuboi,“asamplingtheoremforperiodicfunctionswithnominusfrequencycomponentanditsapplication,”incommunications(apcc),201319thasia-pacificconferenceon.ieee,2013,pp.225–230.[11]stephanemallat,awavelettourofsignalprocessing,2nded.,academicpress,1999.[12]georgecstey,“upperboundsontimejitterandsamplingrateerrors,”inieeproceedingsg-electroniccircuitsandsystems.iet,1983,vol.130(5),pp.210–212.[13]jingfanlong,peixinye,andxiuhuayuan,“truncationerrorandaliasingerrorforwhittaker-shannonsamplingexpansion,”incontrolconference(ccc),201130thchinese.ieee,2011,pp.2983–2985.[14]wenchangsunandxingweizhou,“samplingtheoremforwaveletsubspaces:errorestimateandirregularsampling,”ieeetransactionsonsignalprocessing,vol.48,no.1,pp.223–226,2000.[15]holgerbocheandullrichjmoenich,“reconstructionbehaviorofshannonsamplingserieswithoversampling-fundamentallimits,”insourceandchannelcoding(scc),20087thinternationalitgconferenceon.vde,2008,pp.1–6.[16]zhanjiesong,beiliu,yanweipang,chunpinghou,andxuelongli,“animprovednyquist–shannonirregularsamplingtheoremfromlocalaverages,”ieeetransactionsoninformationtheory,vol.58,no.9,pp.6093–6100,2012.[17]chung-hsunhuangandchao-yangchang,“anareaandpowerefficientadder-basedstepwiselinearinterpolationfordigitalsignalprocessing,”ieeetransactionsonconsumerelectronics,vol.62,no.1,pp.69–75,2016.[18]taojiangandyiyanwu,“anoverview:peak-to-averagepowerratioreductiontechniquesforofdmsignals,”ieeetransactionsonbroadcasting,vol.54,no.2,pp.257–268,2008.[19]p.j.davis,interpolationandapproximation.,couriercorporation,1975.[20]p.s.bullen,d.s.mitrinovic,andm.vasic,meansandtheirinequalities.,springerscience&businessmedia,2013.[21]prachipalsodkar,pravindakhole,prasannapalsodkar,andominichandekar,“designofpeakdetectorandsub-flasharchitectureforadaptiveresolutionofflashadc,”inautomation,computing,communication,controlandcompressedsensing(imac4s),2013internationalmulti-conferenceon.ieee,2013,pp.780–784。当前第1页12