一种多分量LFM信号的精确检测与分离方法与流程

本发明涉及信号与信息处理技术，具体涉及一种多分量LFM信号的精确检测与分离方法。

背景技术：

随着大规模复杂雷达系统投入使用，电磁环境日益复杂，大量雷达脉冲交叠从而形成多分量线性调频(Linear frequency modulated,LFM)信号。多分量LFM信号有效检测和分离作为雷达信号有效识别与参数提取的关键问题，在现代电子对抗侦察系统中受到越来越多的重视。多分量LFM信号的检测和分离主要分为参数化方法和非参数化方法，其中非参数化方法主要基于时频分布。巴尔巴罗萨(BARBAROSSA S.)等首先在《Analysis of multicomponent LFM signals by a combined Wigner-Hough transform.》(IEEE Transactions on Signal Processing,1995,43(6):1511-1515)中通过Wigner-Hough变换(WHT)对多分量LFM信号进行了分析，为雷达信号的参数提取与有效识别提供了新的途径。此后，郭汉伟等在《基于小波Radon变换检测线性调频信号》(国防科技大学学报,2003,25(1):91-94)将小波-Radon变换引入LFM信号的检测与参数估计中，在较高信噪比(Signal to Noise Ratio,SNR)条件下实现了信号参数的精确估计。

然而，非参数化信号检测方法易受噪声影响且估计精度较低，部分方法还受到交叉项干扰。因此，傅立叶-贝塞尔变换(Fourier-Bessel Transform,FBT)作为一种参数化方法开始被引入信号检测与分离中。帕彻力(PACHORI R B)等在《A new technique to reduce cross terms in the Wigner distribution》(Digital Signal Processing,2007,17(2):466-474)将FBT引入数字信号处理领域，完成了频域不交叠LFM信号的分离。苏雷什(SURESH P)等在《Extracting micro-Doppler radar signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis》(IEEE Transactions on Geoscience and Remote Sensing,2014,52(6):3204-3210)提出了一种频域交叠信号的分离方法，该方法具有一定的普适性，且在低信噪比下具有一定鲁棒性。然而，对于频率相近的多分量LFM信号，传统基于FBT的方法由于分辨率限制，导致难以对信号分量进行正确检测和有效分离。

技术实现要素：

针对传统基于FBT的方法难以实现多分量LFM信号的精确检测和有效分离，为了在低SNR环境下正确检测频率相近多分量LFM信号并完成信号分离，本发明通过分析FB级数的特点，推导了信号频率成分与FB系数的一一对应关系，指出信号分离精度与FB积分窗长正相关，进而提出了一种基于离散变窗长FBT(Discrete Variable Window Length FBT,DVWL-FBT)的多分量LFM信号的精确检测与分离方法，完成了低SNR环境下频率相近多分量LFM信号的正确检测和有效分离。

本发明提供了一种多分量LFM信号的精细检测与分离方法，包括下列步骤：

第一步：对接收信号进行分数阶Fourier变换(FrFT)，搜索能量聚集峰值及对应分数阶Fourier域，进行信号分量的粗检测；

第二步：对信号进行DVWL-FB级数展开，确定DVWL-FB系数的最小值及最大值系数确定系数区间，通过该区间上系数幅值特性不断更新区间，进行信号检测修正；

第三步：提取最终划分区间的DVWL-FB系数进行信号重构；对重构信号进行分数阶Fourier逆变换(IFrFT)，得到时频域上的原始单分量信号；循环步骤一至二，直到不存在明显的能量聚集峰值。

在本发明的所述方法中，第一步包括：

对接收信号s(t)进行分数阶Fourier变换(FrFT)，搜索能量聚集峰值及分数阶Fourier域，进行信号分量的粗检测；

设多分量LFM信号的模型表示为

式中：K为信号分量数，a_i、f_i、μ_i分别为第i个信号分量的振幅、载频和调频率，w(t)～N(0,σ²)为实部、虚部不相关的零均值复高斯白噪声；LFM信号在时频面上呈直线形式，其FrFT可视为在时频平面上将t轴与f轴绕原点逆时针旋转一定角度后得到的直线形式；信号s(t)的FrFT定义为：

式中：u为分数阶傅立叶域变量，p为变换阶次，α＝pπ/2为变换前后坐标轴夹角，K_α(t,u)为变换核；

t_θ轴和f_θ轴由时频平面上t轴和f轴经FrFT后绕原点逆时针旋转角度θ得到，Δθ为旋转步长；沿轴将该信号时频分布线向轴积分，若满足

则在处取得极大值，即表示在该分数阶Fourier域上某一分量信号表现为单频信号的形式；依次在时频面上进行搜索，即可确定各分量信号对应积分极大值的分数阶Fourier域；此时，该多分量LFM信号可表示为

在本发明的所述方法中，第二步包括：

对信号进行DVWL-FB级数展开，确定DVWL-FB系数的最小值及最大值系数，并根据该区间上系数幅值单调性进行区间划分，实现信号检测修正；

在有限区间(0,T)上，信号s(t)在(0,T)上的各项零阶FB级数展开为

信号s(t)的各项FB级数C_m可由下式计算

式中，m＝1,2,…,M，J₁(λ_m)为一阶Bessel函数在λ_m处的函数值；

已知在能量聚集的分数阶Fourier域上，某一单分量LFM信号表现为单频信号的形式，即s₀(t)＝aexp(j2πf₀t)；由式(6)知，信号s(t)展开的FB级数核函数为k(t)＝J₀(λ_mt/T)，由Bessel函数性质，有

其中λ_m＞2πf₀T；当信号频率f₀趋近于时，m₀阶FB系数表现为一峰值；设频率

则

由式(9)知，当积分上限T一定时，信号频率与FB系数的阶数m存在一一对应关系；该积分峰值即表示存在一频率为f₀的单频信号；

为提高信号的频率分辨率以提高多分量信号的分离精度，现设信号观测时间(0,T)，窗长T′＝kT为信号观测时间的k(k＞1)倍，则

则当上式取得极大值时，频率f₀可近似表示为

已知第m阶和第m+1阶FB系数对应的零阶Bessel函数的正根分别为λ_m和λ_m+1，当m→∞时，两相邻零阶贝塞尔函数正根之差约为π，即

其中，|(λ_m+1-λ_m)-π||_m≥7＜10^-3，即当m≥7时两相邻零阶Bessel函数的正根之差与π之差小于10^-3；因此，当窗长为T′＝kT时，相邻FB系数对应频率的差值Δf_m随系数阶数的增大而微小变化，以该频率差值近似表示频率分辨率，即

由式(13)知，信号的频率分辨率Δf_m与窗长T′(或k值)负相关；窗长(或k值)越大，频率分辨率越高，信号的分离精度越高；

有限时域连续信号在进行信号处理之前通常进行数字采样；若信号观测时间为(0,T)，信号采样频率为f_s，采样间隔为t_s，采样点数为N，则离散多分量LFM信号表示为

当积分窗长为T′＝kT时，则离散信号s(n)的各项DVWL-FB级数表示为

其中m＝1,2,…,M；为降低计算复杂度，对式(15)作如下改进

其中K₁＝2t_s/T²为常系数，系数仅随阶数m变化；式(15)中，计算每一阶系数需进行3N次乘法，N-1次加法，则计算M阶系数的算法复杂度为O(3MN²)；同理，采用式(16)计算M阶系数的算法复杂度为O(2MN²)，计算效率得到提升；

由式(10)知，当积分窗长不变时，信号的频率与DVWL-FB级数的阶数一一对应；已知N个采样点所表示的最大频率为Nf_s，则必然存在某一最大有效阶数M与该最大频率相对应，即M＝kN；因此对于离散信号，只需计算阶数为k倍信号采样点数的DVWL-FB级数即可完全表征采样的信号频率范围；由此可以得出，窗长的增大一方面使得信号的频率分辨率提高，达到更优的信号分离精度，另一方面使得所需计算DVWL-FB系数的阶数增加，计算量相应增大；

在本发明的所述方法中，第三步包括：

提取最终划分区间的DVWL-FB系数进行信号重构；对重构信号进行分数阶Fourier逆变换(IFrFT)，得到时频域上的原始信号；循环步骤一至二，直到不存在明显的能量聚集峰值；

其中，由于FrFT计算量对步长的限制，使得变换后的各分量信号仍存在一较小带宽而非理论单频信号；同时，如式(11)所述，某一单频信号除峰值阶数外在其附近若干阶系数上也存在投影；因此，变换后的信号除峰值项DVWL-FB系数外还与其附近的若干项系数有关；

由于最大值和最小值项DVWL-FB系数总是成对出现，因此依次提取该区间上系数并进行重构，即可得到分数阶Fourier域的各单分量信号，从而完成信号在分数阶Fourier域的分离；已知多分量信号的DVWL-FB系数表现为各个单分量信号系数的叠加，即

因此，第i个信号分量可根据区间上的若干项DVWL-FB系数重构为

最后，通过分数阶Fourier逆变换(Inverse Fractional Fourier transform，IFRFT)将分数阶Fourier域的各分量信号还原为时频域信号

可以对信号分量进行正确检测和有效分离。

附图说明

图1示出本发明的流程图；

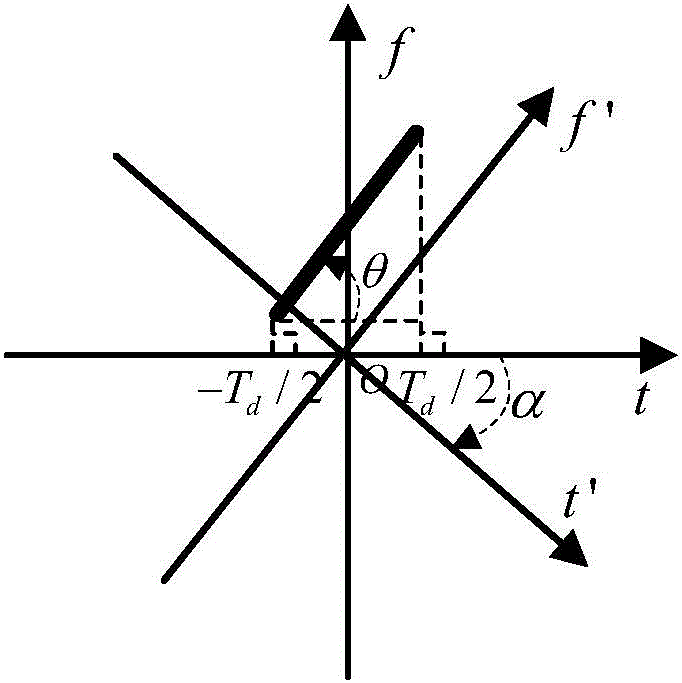
图2示出分数阶Fourier域LFM信号示意图；

图3示出理论条件及SNR＝-8dB条件下多分量LFM信号时频分布图；

图4(a)示出SNR＝-8dB条件下时频域多分量LFM信号的DVWL-FB系数，图4(b)示出SNR＝-8dB条件下分数阶Fourier域多分量LFM信号的DVWL-FB系数，图4(c)示出SNR＝-8dB条件下分数阶Fourier域多分量LFM信号的DVWL-FB峰值系数放大图；

图5(a)示出理论条件下时频域多分量LFM信号的DVWL-FB系数，图5(b)示出理论条件下分数阶Fourier域多分量LFM信号的DVWL-FB系数，图5(c)示出理论条件下分数阶Fourier域多分量LFM信号的DVWL-FB峰值系数放大图；

图6(a)示出采用本发明分离得到的第一信号分量的时频分布图，图6(b)示出分离得到的第二信号分量的时频分布图一，图6(c)示出分离得到的第二信号分量的时频分布图二，图6(d)示出分离得到的第二信号分量的时频分布图三；

图7示出不同SNR条件下，最小可分辨频率随窗长的变化情况。

具体实施方式

下面结合实施例、附图对本发明作进一步描述。

本发明的方法是：首先利用FrFT实现各信号分量的最佳能量聚集，根据峰值个数进行信号分量的粗检测；然后通过设定合适的窗长以达到分离精度要求，根据DVWL-FB级数的幅度特性进行信号分量的检测修正；在信号正确检测基础上，结合逐次消去技术通过DVWL-FB级数重构完成信号分离。

实现上述本发明方法的具体步骤如下：

第一步：初始化信号分量个数K＝0；对接收信号s(t)进行FrFT，搜索接收信号能量聚集呈现峰值的分数阶Fourier域，当在域α＝α₀上取得能量聚集极大值时，记K＝K+1。

对接收信号s(t)进行FrFT，搜索能量聚集为峰值的分数阶Fourier域，当在某一域上取得能量聚集峰值时，记信号分量个数K＝K+1；

设多分量LFM信号的模型表示为

式中：K为信号分量数，a_i、f_i、μ_i分别为第i个信号分量的振幅、载频和调频率，w(t)～N(0,σ²)为实部、虚部不相关的零均值复高斯白噪声。LFM信号在时频面上呈直线形式，其FrFT可视为在时频平面上将t轴与f轴绕原点逆时针旋转一定角度后得到的直线形式，如图2所示。FrFT是Fourier变换的广义形式，它作为一种线性变换，在处理多分量信号时能够有效避免交叉项的干扰。当阶数p＝1时FrFT即表示Fourier变换。信号s(t)的FrFT定义为：

式中：u为分数阶傅立叶域变量，p为变换阶次，α＝pπ/2为变换前后坐标轴夹角，K_α(t,u)为变换核。

图2中，t_θ轴和f_θ轴由时频平面上t轴和f轴经FrFT后绕原点逆时针旋转角度θ得到，其中θ∈(-π/2,π/2)，Δθ为旋转步长。若Δθ足够小，总会存在某一旋转角θ＝θ_i，使得LFM信号的时频分布线垂直于分数阶Fourier域中的轴，沿轴将该信号时频分布线向轴积分，若积分满足

则在f_θ＝f_θi处取得极大值，即表示在该分数阶Fourier域上某一分量信号表现为单频信号的形式。依次在时频面上进行搜索，即可确定各分量信号对应积分极大值的分数阶Fourier域。此时，该多分量LFM信号可表示为

式(4)表明各分量信号在各自能量聚集为峰值的分数阶Fourier域上表现为单频信号的形式。

然而，多数基于FrFT的多分量信号检测算法将能量聚集的峰值个数作为信号分量个数的判定。然而，与基于能量的Wigner分布相同，基于FrFT的能量聚集峰值判定对噪声敏感。此外，由于计算量对FrFT旋转步长的限制，往往导致频率相近的第i个和第j(j≠i)个信号分量搜索得到的能量聚集表现为单峰。此时，若将峰值个数判定为信号分量数将会产生疏漏。因此，在此基础上，进行第二步的基于DVWL-FB级数的检测修正。

在本发明的所述方法中，第二步包括：

根据信号分离精度要求设定DVWL-FBT窗长，在各能量聚集分数阶Fourier域上对信号进行DVWL-FB级数展开；确定DVWL-FB系数的最小值系数及最大值系数判断该区间上系数i∈[a,b]的单调性；根据系数幅值单调性进行区间划分，每次划分记K＝K+1，以此进行检测修正；

在无限区间上，FBT将信号分解为无限个贝塞尔函数的加权和。通常情况下，多分量LFM信号s(t)为有限时域信号，在有限区间(0,T)上，信号s(t)能够展开为正交函数集上的无穷级数。当该正交函数集为零阶贝塞尔(Bessel)函数时，信号s(t)即展开为FB级数。零阶Bessel函数的正交性可表示为

式中：t∈(0,T)，J₀(t)为第一类零阶Bessel函数，λ_m为J₀(t)＝0的第m个升序正根。信号在(0,T)上的各项零阶FB级数展开为

信号s(t)的各项FB级数C_m可由下式计算

式中，m＝1,2,…,M，J₁(λ_m)为一阶Bessel函数在λ_m处的函数值。

已知在能量聚集的分数阶Fourier域上，某一单分量LFM信号表现为单频信号的形式，即s₀(t)＝aexp(j2πf₀t)。由式(7)知，信号s(t)展开的FB级数核函数为k(t)＝J₀(λ_mt/T)，由Bessel函数性质，有

其中λ_m＞2πf₀T。当信号频率f₀趋近于时，m₀阶FB系数表现为一峰值。设频率

则

由式(10)知，当积分上限T一定时，信号频率与FB系数的阶数m存在一一对应关系。该积分峰值即表示存在一频率为f₀的单频信号。

频率相近信号的分离对信号的频率分辨率提出了更高的要求。为提高信号的频率分辨率以提高多分量信号的分离精度，设信号观测时间(0,T)，窗长T′＝kT为信号观测时间的k(k＞1)倍，则

则当上式取得极大值时，频率f₀可近似表示为

已知第m阶和第m+1阶FB系数对应的零阶Bessel函数的正根分别为λ_m和λ_m+1，当m→∞时，两相邻零阶贝塞尔函数正根之差约为π，即

实际中，|(λ_m+1-λ_m)-π||_m≥7＜10^-3，即当m≥7时两相邻零阶Bessel函数的正根之差与π之差小于10^-3。因此，当窗长为T′＝kT时，相邻FB系数对应频率的差值Δf_m随系数阶数的增大而微小变化，以该频率差值近似表示频率分辨率，即

由式(14)知，信号的频率分辨率Δf_m与窗长T′(或k值)负相关。窗长(或k值)越大，频率分辨率越高，信号的分离精度越高。

在实际应用中，有限时域连续信号在进行信号处理之前通常进行数字采样。若信号观测时间为(0,T)，信号采样频率为f_s，采样间隔为t_s，采样点数为N，则离散多分量LFM信号表示为

当积分窗长为T′＝kT时，则离散信号s(n)的各项DVWL-FB级数表示为

其中m＝1,2,…,M。为降低计算复杂度，对式(16)作如下改进

其中K₁＝2t_s/T²为常系数，系数仅随阶数m变化。已知{λ_m}为一固定常数列，因此{K_m}也为一固定常数列，且各阶系数不随信号参数的不同而改变。式(16)中，计算每一阶系数需进行3N次乘法，N-1次加法，则计算M阶系数的算法复杂度为O(3MN²)。同理，采用式(17)计算M阶系数的算法复杂度为O(2MN²)，计算效率得到提升。

由式(11)知，当积分窗长不变时，信号的频率与DVWL-FB级数的阶数一一对应。已知N个采样点所表示的最大频率为Nf_s，则必然存在某一最大有效阶数M与该最大频率相对应，即M＝kN。阶数大于最大有效阶数M的DVWL-FB系数对应的信号频率为第1～M阶系数对应信号频率的周期性重复，其重复周期M_r为2倍采样点数，即M_r＝2kN。特别地，取窗长为信号观测时间时，最大有效阶数即为信号采样点数。因此对于离散信号，只需计算阶数为k倍信号采样点数的DVWL-FB级数即可完全表征采样的信号频率范围。由此可以得出，窗长的增大一方面使得信号的频率分辨率提高，达到更优的信号分离精度，另一方面使得所需计算DVWL-FB系数的阶数增加，计算量相应增大。

如前所述，将基于FrFT能量聚集峰值个数判定为信号分量数将会产生疏漏。由式(4)知，某一信号分量当能量聚集取得峰值时转换为单频信号。根据信号频率与DVWL-FB级数项数的关系，该单频信号总会在某项DVWL-FB系数上取得峰值。同时，由于Bessel函数的振荡特性，使得该峰值系数表现为相邻的正负两项峰值系数，即最大值和最小值。根据频率分辨率与窗长的关系，窗长(或k值)的增加使得频率分辨率提高，具体通过在最小值系数和最大值系数之间插入若干项系数来实现(不妨设a＜b)，且这些系数在以该最大值和最小值系数构成的区间上单调增加(或单调减小)。

对于多个频率相近的信号分量，其DVWL-FB系数在该区间上叠加，从而使得单分量信号幅值的单调性被破坏。因此，在基于FrFT能量聚集的基础上，通过以最大值和最小值系数构成区间上的DVWL-FB系数幅值的单调性进行频率相近信号的检测修正个数判定，不仅在频率分辨率上有所提高，且不易受噪声影响。

在本发明的所述方法中，第三步包括：

提取最终划分区间的DVWL-FB系数进行信号重构；对重构信号进行分数阶Fourier逆变换(IFrFT)，得到时频域上的原始信号。循环步骤一至二，直到不存在明显的能量聚集峰值。

实际中，由于FrFT计算量对步长的限制，使得变换后的各分量信号仍存在一较小带宽而非理论单频信号。同时，如式(11)所述，某一单频信号除峰值阶数外在其附近若干阶系数上也存在投影。因此，变换后的信号除峰值项DVWL-FB系数外还与其附近的若干项系数有关。

由于最大值和最小值项DVWL-FB系数总是成对出现，因此依次提取该区间上系数并进行重构，即可得到分数阶Fourier域的各单分量信号，从而完成信号在分数阶Fourier域的分离。已知多分量信号的DVWL-FB系数表现为各个单分量信号系数的叠加，即

因此，第i个信号分量可根据区间上的若干项DVWL-FB系数重构为

最后，通过分数阶Fourier逆变换(Inverse Fractional Fourier transform，IFRFT)将分数阶Fourier域的各分量信号还原为时频域信号

实例：空间锥体目标干涉式三维成像与微动特征提取仿真实验

仿真参数设定：信噪比SNR＝-8dB条件下，信号观测时间T＝20μs，采样频率F_s＝51.2MHz。分量s₁：f₁＝12MHz，μ₁＝-4.25×10¹¹Hz/s，a₁＝1.5；分量s₂：f₂＝7MHz，μ₂＝6×10¹¹Hz/s，a₂＝1.5；分量s₃：f₃＝21MHz，μ₃＝1.25×10¹¹Hz/s，a₃＝1；分量s₄：f₄＝20.9MHz，μ₄＝1.25×10¹¹Hz/s，a₄＝1。其中s₁与s₂的时频分布在时频域交叠，s₃与s₄为频率相近信号，其调频率相同，起始频率仅相差0.1MHz。针对上述设定的参数进行仿真，在理论条件下和SNR＝-8dB条件下，频率相近多分量LFM信号模型如图3所示。

图3(a)-图3(c)表明：①频率相近多分量LFM信号s₃与s₄从时频分布图上几乎无法区分，如图3(a)所示；②加入-8dB的高斯白噪声后，多分量信号的SPWVD难以反映信号的时频特征，如图3(b)所示。

采用所提出的多分量LFM信号精细检测与分离算法对各信号分量能量聚集的分数阶Fourier域进行搜索，设置搜索角度步长为0.0002rad，当搜索到0.9746rad时，得到了分量s₃和分量s₄能量聚集的分数阶Fourier域，记信号分量数K＝1。图4(a)示出了取k＝6时且SNR＝-8dB条件下，时频域及分量s₃与分量s₄能量聚集的分数阶Fourier上多分量LFM信号的DVWL-FB级数，图4(b)示出了该域上分量s₃和分量s₄的峰值DVWL-FB系数及其周围若干阶的局部放大图，其中DVWL-FB系数幅值的最大值和最小值阶数分别在第4563阶和第4600阶取得，幅值分别为-80.35和93.26。图5(a)和图5(b)分别示出了理论条件下相应的DVWL-FB级数及局部放大图。

由于在第4563阶和第4600阶构成的区间上，DVWL-FB系数幅值不具有单调性，将该区间分割为两个区间第4553阶到第4563阶和第4600阶到第4610阶，在这两个区间上DVWL-FB系数幅值单调减小。因此在此区间上的单分量信号已完全检测出，记信号分量数K＝K+1，即K＝2。

图4(a)-图4(c)，图5(a)-图5(c)表明：①在时频域上DVWL-FB系数不能明显地反映信号特征，表现为一系列杂乱无章的系数；②在能量聚集的分数阶Fourier域上，DVWL-FB系数在m_min＝4563阶和m_max＝4600阶分别取得最小值和最大值，且在以m_min和m_max构成的的DVWL-FB系数区间上非单调性，表明该区间系数对应并非单分量信号。③SNR＝-8dB条件下分量s₃与s₄的DVWL-FB系数的最大幅值和最小幅值阶数与理论条件下所得系数相同，证明了噪声条件下本发明所提方法的正确性。

以此类推，继续进行能量聚集的分数阶Fourier域的搜索，将分数阶Fourier域上信号展开为DVWL-FB级数并按照相应阶数重构。图6(a)-图6(d)示出了采用所提方法进行多分量LFM的分离结果。可以看出，采用基于DVWL-FBT的信号检测与分离算法，频率相近信号及时频域交叠信号均完成了有效分离，同时噪声也被有效抑制，各分量的时频分布较好的反应了各自的时频特征，说明了本发明所提方法的有效性。

高斯白噪声背景下，对频率相近多分量信号进行检测正确性测试。待分离信号为频率相近两分量信号s₅与s′₅，其中f₅＝10MHz，f′₅＝10+Δf MHz，其余参数均相同。在SNR为12dB～-6dB条件下，采用200次Monte-Carol方法仿真测试基于DVWL-FBT算法的两分量信号的检测正确性。由于两信号频率相近，当其频率差小于一定值时，算法无法正确检测出正确信号分量个数，称能够正确检测的信号频率差值为最小可分辨频率Δf,这一频率与载频的比值称为最小可分辨百分比。图7示出了不同SNR条件下，检测正确概率大于90％的最小可分辨百分比随窗长(K值)变化情况。

该方法能够在低信噪比条件下，对频率相近的多分量LFM信号实现精确检测和有效分离，在信号检测正确性、信号分离精度以及低信噪比鲁棒性等方面具有明显优势。