一种二维相关信号建模方法与流程

本发明属于无线通信及信号处理
技术领域：
，涉及无线通信信道建模和二维相关信号构建，具体涉及一种二维相关信号建模方法。
背景技术：
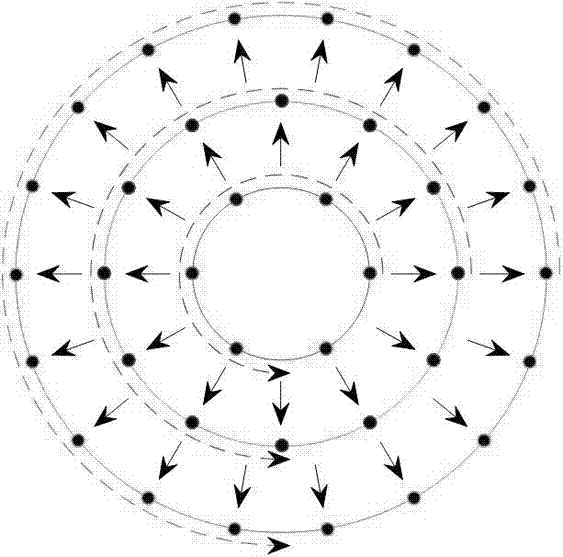
：在无线通信和信号处理领域，有多种信号具有空间相关的特性。在无线通信中，信号从同一个发射端到相近的接收位置，或者从相近的发射端到相同的接收位置，或者从相近的发射端到相近的接收位置，都具有相关性，相关程度与发射端之间或者接收端之间的距离有关。无线传输信号的相关性由传输环境决定，无线信道反应环境对传输信号的影响。从信号发射端到接收端之间的信道状态直接影响接收信号的质量，因而通信系统性能与无线信道具有密切关系。信道建模和信道参数估计在无线通信研究开发过程中具有至关重要的作用。无线通信的信道由路径损耗、阴影衰落和小尺度衰落来表征。路径损耗是信号发射端到接收端之间距离的函数，可表示为参考距离损耗与相对距离的指数运算之和，其中指数一般为2～4之间的实数。阴影衰落由信号传输过程中的障碍物遮挡引起，衰落强度一般可表示为对数正态分布。小尺度衰落由信号的多径传输引起，多个随机信号叠加使信号的幅度呈现瑞利分布。无线信道建模是无线通信研究开发尤其是在链路仿真和系统仿真过程的关键环节。阴影衰落是信道的重要组成部分，反应环境对信号的影响，具有空间相关性。从同一个发射端到两个不同位置的接收端，在与障碍物尺度相当的空间范围，信号的阴影衰落具有关联性，这种相关为阴影衰落的自相关。从不同发射端到同一接收端的信号阴影衰落之间的相关称为阴影衰落的互相关。描述阴影衰落自相关的模型有很多种，其中最常用的是指数衰减的相关模型。如果A、B两点之间的距离为d，这两点的阴影衰落值PA和PB用dB表示分别为sA＝10log10(PA)和sB＝10log10(PB)，那么它们之间的相关系数可表示为其中σA和σA分别表示sA和sB的均方根，d0为阴影衰落相关距离。在对某一区域的阴影衰落进行建模时，为了满足阴影衰落的相关性，可以采用乔里斯基分解方法或者滤波的方法。首先对区域进行网格划分，产生和网格节点数相对应的统计独立同分布的高斯变量，然后对变量进行加权获得各端点的阴影衰落值。为了获得加权系数，首先根据距离关系构建网格节点间的阴影衰落相关矩阵，然后用乔里斯基分解方法求相关矩阵的平方根。当节点个数较多时，该方法由于复杂度过高而难于实现；滤波的方法根据节点间的相关系数构造一阶或多阶滤波器，滤波的方法在一维空间比较有效，但是在二维空间误差较大。技术实现要素：发明目的：为了克服现有技术中存在的不足，提供一种二维相关信号建模方法，所产生的信号满足相关的特性，适用于相关系数是距离的函数的场景，该方法可用于无线通信信道相关阴影衰落建模，也可用于其它的信号具有类似的二维相关特性的领域。技术方案：为实现上述目的，本发明提供一种二维相关信号建模方法，包括如下步骤：步骤1：区域分割和量化：以建模区域中心为圆心，构造多个圆，圆的半径依次增大，将该区域分割为多个圆环，并在每个圆周上以等间隔布置点，随半径增大，圆周上点数增加，使这些点在整个区域近似均匀，设第n个圆共Nn个点，以顺时针方向对圆上的各点编号依次为0,1,…,Nn-1；步骤2：变量初始化：产生和步骤1中点数相同的统计独立同分布的随机变量，并将变量与步骤1中的点相对应，第n个圆上的初始变量表示为xn,i，i＝0,1,…,Nn-1；步骤3：第一个圆上各点相关变量构建，其具体步骤如下：步骤3.1：设第一个圆上各点以顺时针方向编号依次为0,1,…,N1-1，点0到点i，i＝0,1,…,N1-1，的距离为d1,i，对于信号相关为距离函数场景，点0和点i信号的协方差E{s1,0s1,i}为di的函数f(d1,i)·σ2，其中σ2为信号方差；步骤3.2：第一个圆上点0,1,…,N1-1的初始变量表示为向量x1＝[x1,0,x1,1,…,x1,N1-1]t，[·]t表示转置；步骤3.3：第一个圆上点中点0和点0,1,…,N1-1信号相关系数表示为向量f(d)表示d的函数；步骤3.4：设F1为长度为N1的傅立叶变换矩阵，为长度为N1的傅立叶逆变换矩阵，计算λ1＝F1c1及其中diag(x)表示以向量x为对角线构造的对角矩阵；步骤3.5：计算得到第一个圆上各点的相关变量。步骤4：第n(n＞1)个圆上各点相关变量构建，其具体步骤如下：步骤4.1：已得到的第n-1个圆上的Nn-1个点的相关变量为点0和点i(i＝0,1,…,Nn-1-1)的距离为dn-1,i，相关系数为f(dn-1,i)，相关系数表示为向量步骤4.2：第n个圆上一点p和第n-1个圆上的点i，i＝0,1,…,Nn-1-1，的距离为tn,p,i，相关系数为f(tn,p,i)，相关系数表示为向量步骤4.3：设Fn-1和Fn分别为长度Nn-1和Nn的傅立叶变换矩阵，和分别为长度Nn-1和Nn的傅立叶逆变换矩阵，计算λn-1＝Fn-1cn-1及Zn-1＝diag(1./λn-1)，其中diag(x)表示以向量x为对角线构造的对角矩阵，./表示除以每个元素；步骤4.4：计算步骤4.5：计算步骤4.6：计算及步骤4.7：令这里kn是调整系数，使步骤4.10的结果误差最小；步骤4.8：计算及步骤4.9：计算(x)p表示向量x的第p个元素；步骤4.10：计算根据步骤4.1～4.5，是由第n-1个圆上已得到的相关变量加权合成，以满足和第n-1个圆上点的相关性；根据步骤4.7～4.9，由第n个圆上点的初始变量合成，以补偿第n个圆上点的相关性；根据步骤4.6，βn,p用来满足变量sn,p的方差约束；步骤4.11：循环执行步骤4.1～4.7得到第n(n＞1)个圆上所有点相关变量sn,p，其中p＝0,1,…,Nn-1。步骤5：循环执行步骤4得到所有圆周上各点的相关变量。有益效果：本发明与现有技术相比，构造了具有循环对称结构的图形，利用循环移位矩阵的性质将复杂的矩阵分解和矩阵求拟问题转换为简单的运算，降低了运算复杂度，该方法构建的信号充分满足二维相关特性，具有精度高，复杂度低，实现简单的特点，与现有的乔里斯基分解方法相比，本方法采用傅立叶变换方法，避免了矩阵求逆和矩阵分解，其复杂度有了大幅降低，与现有的线性滤波方法相比，本方法的精度有了明显提高，完全满足二维空间的使用需求。附图说明图1为本发明中步骤1中覆盖建模区域的圆和点的示意图；图2为本发明中信号构建过程的示意图；图3为n＝2～11时最佳调整系数和拟合曲线示意图；图4为本发明方法和线性滤波方法的线性结果对比图。具体实施方式下面结合附图和具体实施例，进一步阐明本发明，应理解这些实施例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。实施例1：利用本发明的方法构建指数衰减相关的阴影衰落模型，假设A、B两点之间的距离为d，这两点的阴影衰落值用dB表示分别为sA和sB，那么它们之间的相关系数可表示为其中σsf表示阴影衰落的均方根，d0为阴影衰落相关距离，则该相关阴影衰落的信号建模过程如下：步骤1：如图1所示，以建模区域中心为圆心，以mr为半径构造多个圆，这里m＝1,2,…M，M是圆的个数，在第m个圆上等间隔布置6m个点，每个圆上的点以顺时针编号；步骤2：产生和上述步骤1中点数相同的统计独立同分布的随机变量，分布为N(0,σsf)，并将变量与图1中的点相对应，第m个圆上的初始变量为xm,i，i＝0,1,…,6m-1；步骤3：第一个圆上各点相关变量构建，其具体步骤如下：步骤3.1：设第一个圆上各点以顺时针方向编号依次为0,1,…,N1-1，点0到点i，i＝0,1,…,N1-1，的距离为d1,i，对于信号相关为距离函数场景，点0和点i信号的协方差E{s1,0s1,i}为di的函数f(d1,i)·σ2，其中σ2为信号方差；步骤3.2：第一个圆上点0,1,…,N1-1的初始变量表示为向量[·]t表示转置；步骤3.3：第一个圆上点中点0和点0,1,…,N1-1信号相关系数表示为向量f(d)表示d的函数；步骤3.4：设F1为长度为N1的傅立叶变换矩阵，为长度为N1的傅立叶逆变换矩阵，计算λ1＝F1c1及其中diag(x)表示以向量x为对角线构造的对角矩阵；步骤3.5：计算得到第一个圆上各点的相关变量：第一个圆上各点相关变量为其中F1为长度为6的傅立叶变换矩阵，为长度为6的傅立叶逆变换矩阵，λ1＝F1c1，步骤4：第n(n＞1)个圆上各点相关变量构建，其具体步骤如下：步骤4.1：已得到的第n-1个圆上的Nn-1个点的相关变量为点0和点i(i＝0,1,…,Nn-1-1)的距离为dn-1,i，相关系数为f(dn-1,i)，相关系数表示为向量步骤4.2：第n个圆上一点p和第n-1个圆上的点i，i＝0,1,…,Nn-1-1，的距离为tn,p,i，相关系数为f(tn,p,i)，相关系数表示为向量步骤4.3：设Fn-1和Fn分别为长度Nn-1和Nn的傅立叶变换矩阵，和分别为长度Nn-1和Nn的傅立叶逆变换矩阵，计算λn-1＝Fn-1cn-1及Zn-1＝diag(1./λn-1)，其中diag(x)表示以向量x为对角线构造的对角矩阵，./表示除以每个元素；步骤4.4：计算步骤4.5：计算步骤4.6：计算及步骤4.7：令这里kn是调整系数，使步骤4.10的结果误差最小；步骤4.8：计算及步骤4.9：计算(x)p表示向量x的第p个元素；步骤4.10：计算根据步骤4.1～4.5，是由第n-1个圆上已得到的相关变量加权合成，以满足和第n-1个圆上点的相关性；根据步骤4.7～4.9，由第n个圆上点的初始变量合成，以补偿第n个圆上点的相关性；根据步骤4.6，βn,p用来满足变量sn,p的方差约束；步骤4.11：循环执行步骤4.1～4.7得到第n(n＞1)个圆上所有点相关变量sn,p，其中p＝0,1,…,Nn-1。其中第n(1＜n≤M)个圆上点p的相关变量为其计算包括以下过程：a)相关系数向量计算：点p和第n-1个圆上点i的相关系数为其中tn,p,i是点p和第n-1个圆上的点i的距离，i＝0,1,…,Nn-1-1，向量b)加权系数αn,p计算：根据步骤4.1～4.4，这里Fn-1和分别是长度Nn-1的傅立叶变换矩阵和逆矩阵，Zn-1＝diag(1./λn-1)，是第n-1个圆上点0和所有点的相关系数构成的向量，dn-1,i表示第n-1个圆上点0和点i的距离。c)计算d)计算及e)计算相关系数这里dn,i表示第n个圆上点0和点i的距离，μ是一个与r有关的调整系数(关于调整系数在下面有进一步的说明)；f)计算根据步骤4.8和步骤4.9,这里设Fn和分别为长度Nn的傅立叶变换矩阵和逆变换矩阵；g)计算h)循环执行a)～g)得到第n(n＞1)个圆上所有点相关变量sn,p，p＝0,1,…,Nn-1。步骤5：循环执行过程a)～h)得到所有圆周上各点的相关变量，整个过程如图2示意。实施例2：关于实施例1中计算过程e)中的调整系数μ的说明和分析表1～表3给出了在n＝2，n＝4，及n＝11情况下，对不同的相对半径r/d0从0.1到1时的最佳调整系数及对应的绝对误差和相对误差。经过调整之后，同理论值相比，不管是绝对误差还是相对误差都非常小。在相同的情况下，对应最小绝对误差和最小相对误差的调整系数都非常接近。在r/d0相同时，对不同的n，最佳调整系数非常接近，这可以从图3看出。图3给出了n＝2,3,…,11的10种情况下对应r/d0从0.05到2的最佳调整系数，可以看到不同的n对应的系数曲线基本重合。所以在r给定时，对不同圆周建模可采用相同的调整系数，图3中的曲线可以用下面函数拟合，自变量为r/d0，函数值为最佳调整系数。表1，n＝2时调整系数和误差r/d0μ绝对误差μ相对误差0.18.086.67E-058.28.65E-050.24.251.65E-044.382.75E-040.32.992.32E-043.114.93E-040.42.362.59E-042.486.99E-040.51.992.53E-042.18.68E-040.61.752.27E-041.859.91E-040.71.581.92E-041.681.07E-030.81.461.55E-041.551.10E-030.91.371.21E-041.451.09E-0311.39.11E-051.381.04E-03表2，n＝4时调整系数和误差r/d0μ绝对误差μ相对误差0.17.156.30E-077.158.12E-070.23.882.91E-063.894.48E-060.32.786.82E-062.811.29E-050.42.241.11E-052.272.61E-050.51.911.44E-051.954.26E-050.61.71.61E-051.746.07E-050.71.541.63E-051.597.76E-050.81.431.51E-051.479.17E-050.91.351.32E-051.391.01E-0411.281.10E-051.321.07E-04表3，n＝11时调整系数和误差实施例3：本方法与乔里斯基分解法对比：本方法和乔里斯基分解法的复杂度都和建模区域散布的点数有关。乔里斯基分解法需要计算相关矩阵的均方根，复杂度是点数的三次方。本方法采用傅立叶变换方法，避免了矩阵求逆和矩阵分解，复杂度大为降低。对于N点的傅立叶变换，复杂度为Nlog2N。如果一个区域分割为n×n个方格，那么散布的点数为n2，相关矩阵为n2×n2。应用本方法建模，每一个圆周上的点做4次傅立叶变换，傅立叶变换大小是圆周上的点数，总的计算次数近似为2n2log2n，乔里斯基分解法的复杂度为n6。本发明方法和乔里斯基分解法的复杂度对比如下表4所示：表4本发明方法和乔里斯基分解法的复杂度对比n×n4×48×816×1632×3264×64乔里斯基分解法40962621441.68e+71.07e+096.87e+10本发明方法6438420481024049152本发明方法与线性滤波方法对比：图4将本发明方法得到的实验结果与线性滤波方法结果对比进行了对比，可以看到本发明方法明显具有更高的精度。当前第1页1 2 3