一种基于量子粒子群算法的空间机器人预测控制方法与流程

本发明涉及一种空间机器人预测控制方法，属于空间操作与控制
技术领域：
。
背景技术：
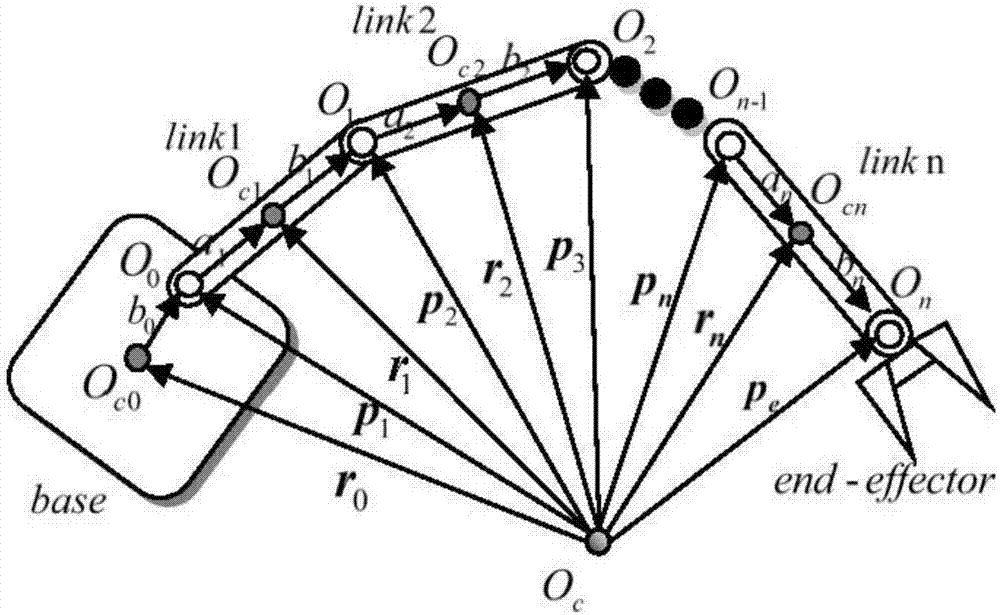
：近年来，随着空间技术的发展，人类太空活动日益频繁。考虑到太空环境的恶劣性以及空间任务的复杂性，用空间机器人代替宇航员完成空间任务就成为必然趋势。但是，与地面固定基座机器人不同，空间机器人基座与机械臂之间的动力学耦合为其动力学建模与控制带来了极大的困难。为了求解空间机器人这种高度非线性系统的动力学与控制问题，学者们提出了不少的方法。umetani和yoshida基于动量守恒的原理提出了反映空间机器人速度级运动特性的广义雅可比矩阵，并在此基础上提出了分解运动速度控制的方法，实现了机械臂末端对期望速度的跟踪。parlaktuna和ozkan根据动力学等价机械臂模型将空间机器人的控制问题从惯性空间转化到了关节空间，得到了参数线性化的关节空间动力学方程，并设计了用于空间机器人关节空间轨迹跟踪控制的pd控制器。齐乃明、张文辉等人为解决空间机器人系统参数不确定性问题，提出了一种神经网络自适应补偿控制方法，该方法引入gl矩阵和乘法算子来辨识系统不确定性参数，大大降低了运算量。然而，上述这些方法也仅仅只是考虑了系统的不确定性以及干扰的影响，并未考虑关节角范围、控制力矩输入、避奇异等各类约束，也无法对力矩进行优化。20世纪70年代以来，随着模型预测控制在工业生产中的兴起，越来越多的预测控制方法涌现出来。由于该控制策略具有控制效果好、鲁棒性强、对模型精确性要求不高以及可以在线处理各类约束的优点，学者们尝试将其应用于航空航天领域，也取得了不少的研究成果。rybus在没有对空间机器人系统进行线性化处理的情况下，采用非线性模型预测控制的方法实现了对末端期望轨迹的跟踪控制，并与逆运动学控制方法和改进的简单自适应控制方法进行了对比。wang等人采用反馈线性化的方法对空间机器人系统模型进行处理，提出了一种考虑避障约束的非线性模型预测控制方法，证明了该方法的有效性，但由于其采用了反馈线性化的处理方法，因此在控制过程中需要事先进行任务空间轨迹规划，才能得到参考的关节角和关节角速度信息。宗立军在wang的基础上提出了一种空间机器人混合整数预测控制方法，该方法基于命题逻辑建立了控制过程中各约束的优先级，有效弥补了模型预测控制方法用于空间机器人控制时，多约束可能导致控制失效的不足。由于采用了约束优先级的定义，因此并不是所有约束都会得到满足。由于采用了约束优先级的定义，因此并不是所有约束都会得到满足。技术实现要素：为了克服现有技术的不足，本发明提供一种基于量子粒子群算法的空间机器人预测控制方法，能够在满足各类约束的情况下实现对末端期望轨迹的有效跟踪，从而为考虑约束的空间机器人轨迹跟踪控制提供了一种新的思路。本发明解决其技术问题所采用的技术方案包括以下步骤：(1)基于动量守恒的原理建立空间机器人速度级运动学模型，求出系统的广义雅克比矩阵；将系统基座看成虚拟连杆，采用扩展机械臂法建立空间机器人拉格朗日动力学模型；然后选取系统的状态变量、输入变量以及输出变量，结合运动学模型和动力学模型，建立离散化的系统状态空间模型；(2)引入扩展状态变量，基于系统状态空间模型建立关于控制输入增量的扩展状态空间模型；应用拉盖尔函数将控制输入增量表示为拉盖尔多项式的形式，在此基础上给定系统的性能指标，并将其转化为二次型性能指标；(3)引入系统输入约束和状态约束，基于拉盖尔多项式，将系统输入约束和状态约束转化为关于待优化参数的矩阵不等式；该矩阵不等式与步骤(2)中的二次型性能指标联立，构成一个受线性不等式约束的二次规划问题；(4)在二次型性能指标中引入惩罚函数对不等式约束进行处理，在此基础上采用量子粒子群算法对二次规划问题进行优化求解，得到下一时刻系统的控制输入；(5)用得到的控制输入更新系统状态，重复上述步骤，直至控制过程结束。本发明的有益效果是：(1)能够在给定约束的情况下实现对末端期望轨迹的有效跟踪，并且不需要事先进行任务空间轨迹规划；(2)能避免出现多约束情况下采用常规二次规划算法找不到全局最优解的情况；(3)能在满足跟踪精度要求的同时对能量消耗进行优化。附图说明图1是空间机器人系统示意图；图2是空间机器人预测控制器结构示意图；图3是平面二杆空间机器人示意图；图4是末端跟踪轨迹示意图；图5是末端位置跟踪误差示意图；图6是末端速度跟踪误差示意图；图7是基座姿态角和关节角示意图；图8是基座姿态角速度和关节角速度示意图；图9是关节力矩(控制输入)示意图。具体实施方式下面结合附图和实施例对本发明进一步说明，本发明包括但不仅限于下述实施例。本发明的思路是：首先基于扩展机械臂法建立空间机器人系统的拉格朗日动力学模型，将其与运动学模型结合建立离散化的状态空间模型；然后，基于系统扩展状态空间模型和拉盖尔多项式设计相应的离散模型预测控制器，最后，采用量子粒子群算法对约束情况下的性能指标进行滚动优化，并对预测误差进行反馈校正，从而实现末端对期望轨迹的有效跟踪。具体求解方法如下：(1)基于动量守恒的原理建立空间机器人速度级运动学模型，求出系统的广义雅克比矩阵。将系统基座看成虚拟连杆，采用扩展机械臂法建立空间机器人拉格朗日动力学模型。然后选取系统的状态变量，输入变量以及输出变量，结合运动学模型和动力学模型，建立离散化的系统状态空间模型。(2)为了使得滚动优化和反馈校正同步进行，引入扩展状态变量，基于步骤(1)的状态空间模型，建立关于控制输入增量的扩展状态空间模型。应用拉盖尔函数将控制输入增量表示为拉盖尔多项式的形式，在此基础上给定系统的性能指标，并将其化为二次型的形式。(3)引入系统输入约束和状态约束，基于步骤(2)中的拉盖尔多项式，将这些约束转化为关于待优化参数的矩阵不等式。该矩阵不等式与步骤(2)中的二次型性能指标联立，构成一个受线性不等式约束的二次规划问题。(4)在步骤(2)的性能指标中引入惩罚函数对不等式约束进行处理，在此基础上采用量子粒子群算法对步骤(3)中的二次规划问题进行优化求解，得到下一时刻系统的控制输入。(5)用得到的控制输入更新系统状态，重复上述步骤，直至控制过程结束。本发明的实施例包括以下步骤：第一步，如图1所示为空间机器人系统示意图。图中oc表示系统质心，oc0表示基座质心，o0为基座与连杆1之间的关节，r0∈r3为基座质心位置矢量，b0为oc0到o0的位置矢量，oi为连杆i与连杆i+1之间的关节，oci表示连杆i的质心，ri∈r3为oc到oci的位置矢量，pi∈r3为oc到oi-1的位置矢量，pe∈r3为末端位置矢量，ai为oi-1到oci的位置矢量，bi为oci到oi的位置矢量，其中i＝1,2,...,n为连杆编号,n为连杆数量。从图1中可以看出，空间机器人末端位置矢量可以表示为如下的形式：对上式进行求导，并结合系统动量守恒的特点进行化简，可以得到机械臂末端速度ve和关节角速度之间的关系式如下：式(2)即为空间机器人速度级运动学模型，其中jg即为系统的广义雅克比矩阵。js与jm分别为基座和机械臂的雅克比矩阵，is与im分别为基座和机械臂的惯量矩阵。我们采用类似于研究地面固定基座机器人的方法，将系统基座看成一个六自由度的虚拟连杆，采用扩展机械臂法来建立空间机器人系统的动力学模型。定义系统的广义坐标q＝[qsqm]，其中qs为基座位姿，qs＝[r0q0]，qm为关节角，qm＝[q1q2…qn]，则空间机器人系统的总动能如下：式中，m0，i0，ω0分别为基座的质量、惯量以及角速度，mi，ii，ωi分别为连杆i的质量、惯量以及角速度，m(q)为系统正定对称的惯量矩阵，其表达式如下(这里不作详细推导)：式中，a，b，c，e，f和n的表达式如下(ki表示关节oi-1转动的单位方向矢量)：由于太空环境为微重力环境，因此将系统势能忽略不计，则空间机器人系统的拉格朗日动力学方程如下：式中τ为系统的广义力矩，τ＝[0τm]，其中τm为关节力矩。将式(4)代入式(7)可得系统的动力学模型如下：式中为系统的离心力和科氏力矩阵，其表达式如下：选取系统的状态变量为输入变量为u＝τ，输出变量为(显然ym＝pe)，可以由式(6)建立系统的状态空间模型并离散化如下：式中ad＝eah，cd＝c(kh)。其中h为离散化的时间步长，a，b，c的表达式如下：式中，m为扩展机械臂的自由度，m＝n+6，im表示m×m的单位矩阵，0m表示m×m的零矩阵。定义末端位置跟踪误差如下：e＝ym-yd(9)式中，yd为系统末端期望位置。对上式求导可得末端速度跟踪误差如下：式中，为系统末端期望速度。为了使得滚动优化与反馈校正同步进行，我们在预测模型中引入如下的扩展状态变量：其中，δxm(k)＝xm(k)-xm(k-1)。在空间机器人轨迹跟踪控制的过程中，为了消除初始末端位置误差引起的常值跟踪误差，实现末端期望位置和速度的同时跟踪，引入如下的参考末端速度来代替期望末端速度式中，λ为常数，0<λ<1。重新定义系统输出为通过推导可得到系统的扩展状态空间模型：式中，δu表示系统控制输入增量，ae，be，ce的表达式如下：接下来，应用拉盖尔函数来进行模型预测控制器的设计。假设稳定系统k时刻的脉冲响应是h(k)，对于给定的参数n，h(k)可以表示为：h(k)＝c1l1(k)+c2l2(k)+…+cnln(k)(14)式中，c1,c2,...,cn为由系统确定的拉盖尔系数，l1(k),l2(k),...,ln(k)为标准正交的拉盖尔函数，其与比例因子a有关。在k时刻未来控制输入序列定义为：δu＝[δu(k)δu(k+1)…δu(k+nc-1)]t(15)式中，nc为控制时域，则k+j时刻的控制输入可以看作是如下的脉冲响应的形式：δu(k+j)＝[δ(j)δ(j-1)…δ(j-nc+1)]δu(16)式中，δ(·)表示单位脉冲函数，j＝0,1,...,np。由式(14)和式(16)可知，δu(k+j)可表示为如下的形式：δu(k+j)＝l(j)tη(17)式中，l(j)为拉盖尔近似模型的状态向量，η为对应的拉盖尔系数，η＝[c1c2…cn]t。则在k时刻以后的k+w时刻系统的状态变量和输出变量如下(w＝1,2,...,np)：给定如下的系统性能指标：式中，q，r分别为系统状态和控制输入增量的权重矩阵。将式(15)和(17)带入式(20)中，并根据拉盖尔函数的标准正交性，可将式(20)重新写为如下的形式：式中，rl是n×n的对角矩阵，其对角线元素均相同且大于零。令则式(17)可重新写为：将式(22)代入(21)可得：式中可以看出第三项与η无关，因此要使得性能指标j最优，实质上是使前两项之和最小，即：j＝ηtωη+2ηtψx(k)(24)首先，引入如下的输入约束：δumin≤δu(k+w)≤δumax(25)umin≤u(k+w)≤umax(26)由式(17)可知，式(25)又可写为：δumin≤m0η≤δumax(27)式中，m0的表达式如下(0k代表全零矩阵，其维度与lk(w)相同)：又由于因此式(26)可写为：umin≤m1η+u(k-1)≤umax(28)式中，m1的表达式如下(0k代表全零矩阵，其维度与lk(w)相同)：则输入约束(27)和(28)可以表示为下面的矩阵不等式约束：然后，引入如下的状态约束：由式(8)可以得到系统状态xm的预测值如下：xm＝fxm(k)+фu(31)式中，则式(30)可以写为：上式也可写为如下的矩阵不等式约束：于是，该模型预测控制问题就转化为如下的二次规划问题：式中，根据优化理论可知，当ω为n×n的正定对称矩阵，该规划问题为严格凸二次规划，如果至少有一个向量η满足约束并且目标函数j在可行域有下界，那么该二次规划问题就有一个全局最小值η，并且该值是唯一的。我们采用量子粒子群算法对上述优化问题进行求解。量子粒子群算法与其他优化算法相比，需要调整的参数较少，能很好地收敛到全局最优点，并且具有鲁棒性好、收敛速度快的优点。为了处理式(34)中的不等式约束，我们在量子粒子群算法的适应度函数(性能指标)中引入如下的惩罚函数，则有j＝ηtωη+2ηtψx(k)+μmax(aη-b,0)(35)式中，μ＝[μ1μ2…μc]，c为约束的个数。设粒子数为nc，最大迭代次数为nmax，那么，该算法的流程如下：(1)根据式(27)确定每个粒子的取值范围(一般为0～0.1)，并在取值范围内随机初始化nc个粒子的初始位置。(2)通过式(35)计算每个粒子的适应度函数值，即适应值。令粒子的局部最优位置为初始粒子位置，令全局最优位置为对应于最小适应值的粒子位置。局部最优位置对应的粒子适应值为局部最优值，全局最优位置对应的粒子适应值为全局最优值。(3)更新粒子位置，如果新粒子的适应值小于当前局部最优值，则令新粒子位置为新的局部最优位置。(4)将新的局部最优值与当前全局最优值进行比较，如果新的局部最优值小于当前全局最优值，则令新的局部最优值对应的粒子位置为新的全局最优位置。(5)如果迭代次数未达到nmax，则返回步骤(3)。通过量子粒子群算法优化即可得到使性能指标最优的η的值，将其代入式(17)便可得到最优控制序列，取控制序列的第一个值作为控制输入的增量，对当前系统输入进行校正即可得到下一时刻的系统输入。该发明所设计的预测控制器的结构如图2所示。最后，我们以图3所示的平面二杆空间机器人系统为例，对该发明提出的控制方法进行仿真验证，系统的几何参数如表1所示。表1平面二杆空间机器人几何参数参数基座连杆1连杆2质量(kg)12.94.51.5惯量(kg·m2)0.2080.320.049长度(m)0.3270.620.6仿真参数设置为：预测时域np＝40，控制时域nc＝15，系统状态和控制输入的权重矩阵分别取q＝i12×12，r＝0.1i2×2，拉盖尔多项式的参数取a＝[0.8,0.8]，n＝[8,8]，系统初始状态为x0＝[00000-0.22-0.01902.14-2.71]t，仿真初始时刻为0，仿真时间为t＝20s，仿真步长取h＝0.01s，粒子数nc＝10，粒子最大迭代次数为nmax＝100。末端期望跟踪轨迹的表达式如下：对应的末端期望速度为：跟踪过程中需要满足的输入约束和状态约束条件如下：仿真结果如图4～9所示。由图4可以看出，该控制器可以使空间机器人末端快速有效地跟踪指定的期望轨迹。图5与图6分别是末端位置跟踪误差与末端速度跟踪误差的变化曲线，图7与图8分别是跟踪过程中的基座姿态角与关节角及相应的角速度变化曲线，图9为控制过程中各关节力矩(控制输入)的变化曲线。从图8～9可以看出，跟踪过程中系统状态和控制输入均满足给定的约束条件，证明了所提出方法的有效性。当前第1页12