一种梯形网格有限差分地震波场模拟方法与流程

本发明属于地震勘探技术领域，涉及一种地震波场模拟方法，尤其是一种梯形网格有限差分地震波场模拟方法。

背景技术：

如何精确并有效地求解波动方程已成为地球物理学的一个重要课题，尤其在地震勘探的许多应用中都涉及这一问题，例如地震数据解释、观测系统设计、高精度成像和建立模型等(etgenando’brien,2007)。用于模拟地震波场的常见方法主要有以下几种：有限差分法、有限元法、体积元法、伪谱法和粒子法等(黎昌成和张美根，2018；huandjia,2016)。其中，有限差分法有着计算量小、内存需求少和易于实现等优点，因而在实际应用中被广泛采用(etgenando’brien,2007；黄超和董良国，2009；yaoetal.,2016)。

在传统有限差分方法中，模型中的空间采样步长是固定的，即用固定网格对介质进行离散(dablain，1986)。与固定网格有限差分相比，变网格有限差分可以在兼顾地震波模拟精度的同时提升模拟的效率(moczo，1989；朱生旺等，2007；赵海波和王秀明，2007)。变网格有限差分在低速区域采用细网格剖分，而在高速区则采用粗网格剖分。该方法的关键在于如何处理粗细网格区域的过渡，根据处理方法的不同可以分为基于插值的算法(jastramandbehle,1992；hayashiandburns,1999；wangetal.,2001；pasalicandmcgarry,2010)、基于邻域差分近似的算法(黄超和董良国，2009；孙小东等，2012；takekawaetal.,2015；lietal.,2017)和基于坐标变换的算法(jastramandtessmer,1994；atleetal.,2011；chenandxu,2012)。其中，基于坐标变换的变网格有限差分可以有效避免不同大小网格区域过渡产生的虚假反射，以及较小的附加计算量和网格大小可随速度相应变化的优点。chenandxu(2012)提出梯形网格剖分，并用伪谱法对弹性波波场进行了数值模拟，结果表明梯形网格剖分在计算量和内存消耗上比固定网格剖分有显著降低。

技术实现要素：

针对上述问题，本发明的目的在于针对地震波传播速度由浅入深整体逐渐增大的特点，提出一种基于卷积完美匹配层吸收边界的梯形网格有限差分地震波场模拟方法，该方法利用梯形坐标系设计耦合速度由浅入深逐渐增大的变化，采用卷积完美匹配层吸收边界条件来消除虚假的边界反射，并且在时间效率和电脑内存需求上均显著优于传统的固定网格有限差分算法。

本发明的目的是通过以下技术方案来解决的：

一种梯形网格有限差分地震波场模拟方法，包括以下步骤：

(1)对给定的直角坐标系下的速度模型v(x0,z0)，确定梯形坐标系形状参数γ为：

式中，表示最深层的纵向深度坐标位置，是深度z0处的横向采样间隔，是深度z0处的最大横向采样间隔，是最深层最大横向采样间隔；其中，v^min(z0)是深度z0的最小速度，f0为震源主频率，ng为一个波长内采样点数；

(2)对给定的直角坐标系下的速度模型v(x0,z0)，进行坐标变换将其转换到梯形坐标系的速度模型v(x,z)，坐标变换表达式为：

式中，x和z分别是梯形坐标系下的横向与纵向坐标，α是梯形坐标横向位置参数，在地震波模拟时与震源横向位置相同，γ是梯形坐标系形状参数；

(3)根据步骤(2)中的坐标变换，将直角坐标系(x0,z0)下的cpml条件下二维时域各向同性声波方程变换为梯形坐标系(x,z)下的声波方程：

式中，u＝u(x,z)是梯形坐标系下的压力场，t是记录时间，xs和zs分别是震源在梯形坐标系下的横纵坐标位置，f(t)是震源的时域波形函数，δ(·)表示狄拉克函数，辅助变量ψi和ζi(i∈{x,z})的定义如下：

式中j表示第j个时刻，系数ai和bi(i∈{x,z})表达式如下：

其中δt是时间间隔，r是理论边界反射系数，vmax是模型最大速度，li是cpml随着i变化的吸收厚度，是吸收区域到计算区域的距离，αmax＝πf0，f0是震源主频率；

(4)利用坐标变换，将步骤(3)中的梯形坐标系(x,z)下的声波方程转化为

其中坐标变换定义为：

其中(x',z')是变换后的坐标，θ为沿x方向的网格线与对角线的夹角；

(5)利用高阶有限差分对步骤(4)中的声波方程进行离散，得到cpml边界条件下梯形坐标系中的时间-空间域二维声波方程的差分方程，并利用此差分方程迭代求解，得到各个时刻的波场：

式中表示空间位置(xm,zn)＝(x+(m-1)δx,z+(n-1)δz)和第j个计算时刻点tj＝t0+(j-1)δt处的波场，δx和δz是梯形坐标系横向和纵向空间采样间隔，t0为震源时延；cp和ηp(p＝1,2,…,n)表示空间一阶和二阶偏导差分系数，n是对应于空间差分精度的差分点数；其中δt为时间采样间隔。

本发明进一步的改进在于，步骤(2)的具体过程如下：

采用如下的坐标变换将直角坐标系转换为梯形坐标系：

式中，(x0,z0)是直角坐标系坐标，(x,z)是梯形坐标系坐标；α是梯形坐标横向位置参数，在地震波模拟中与震源横向位置相同；γ是梯形坐标系形状参数；

若梯形坐标系下横向采样间隔为δx，则其对应物理直角坐标系采样间隔δx0和δz0表示为

δx0(z)＝(1+γg(z))δx

δz0(z)＝g(z+δz)-g(z)

若直角坐标系下的速度模型v(x0,z0)中每个深度最小速度表示为v^min(z0)，且保持震源主频率下波数空间采样点数相同，则每个深度最大横向采样间隔表示为

其中f0为震源主频率，ng为一个波长内采样点数。

本发明进一步的改进在于，利用三次样条插值来建立函数g(z)。

本发明进一步的改进在于，步骤(3)的具体过程如下：

在给定的梯形坐标系与直角坐标系转换关系下，利用偏导数的求导规则，将波场关于直角坐标系(x0,z0)的偏导转化为梯形坐标系(x,z)下的偏导；将直角坐标系压力场u(x0,z0)和梯形坐标系压力场u(x,z)分别简化为u0和u，则二者的一阶和二阶偏导关系为：

对于cpml边界条件下直角坐标系中的二维各向同性声波方程：

其中t为记录时间，δ(x)表示狄拉克函数，(x0s,z0s)是震源在直角坐标系中的横纵坐标，f(t)为时域震源函数，辅助变量ψi0和ζi0(i∈{x,z})的结构如下：

在辅助变量ψi0和ζi0(i∈{x,z})的表达式中，j为第j个计算时刻，参数和表达式如下：

其中δt是时间间隔，r是理论边界反射系数，vmax是模型最大速度，是cpml随着i0变化的吸收厚度，是吸收区域到计算区域的距离，αmax＝πf0，f0是震源主频率；

根据两个坐标系间的偏导关系，对于上述cpml边界条件下直角坐标系中的二维各向同性声波方程，其在梯形坐标系下的声波方程为：

式中，u＝u(x,z)是梯形坐标系下的压力场，t是记录时间，xs和zs分别是震源在梯形坐标系下的横纵坐标位置，f(t)是震源的时域波形函数，δ(·)表示狄拉克函数，辅助变量ψi和ζi(i∈{x,z})的结构如下：

系数ai和bi(i∈{x,z})表达式如下：

其中δt是时间间隔，r是理论边界反射系数，vmax是模型最大速度，li是卷积完美匹配层随着i变化的吸收厚度，是吸收区域到计算区域的距离，αmax＝πf0，其中f0是震源主频率。

本发明进一步的改进在于，步骤(4)的具体过程如下：

通过坐标变换将梯形坐标系中cpml边界条件下二维时域各向同性声波方程中出现的空间混合偏导项转换为二阶非混合偏导，定义如下的坐标变换：

式中，(x',z')是变换后的坐标，θ为沿x方向的网格线与对角线的夹角，且满足0<θ<π/2；在此坐标变换下，混合偏导项表示为：

将此式代入梯形坐标系下的声波方程，得到用于波场模拟的声波方程为

本发明进一步的改进在于，步骤(5)的具体过程为：

对步骤(4)中得到的声波方程，空间偏导采用高阶有限差分格式：

其中表示空间位置(xm,zn)＝(x+(m-1)δx,z+(n-1)δz)和时刻tj＝t0+(j-1)δt处的波场，δx和δz是梯形坐标系横向和纵向空间采样间隔，δt为时间采样间隔，t0为震源时延；cp和ηp(p＝1,2,…,n)表示空间一阶和二阶偏导差分系数，n是对应于空间差分精度的差分点数；若梯形坐标系中横向和纵向空间采样间隔相同，则坐标系(x',z')中采样有δx'²＝δz'²＝δx²+δz²，所以

时间偏导数采用2阶，代入并化简后，梯形坐标系中cpml边界条件下时间空间域二维声波方程差分方程为

式中，表示当且仅当m＝m0时，其他时候为0；同理；辅助变量ψi和ζi(i∈{x,z})及他们的偏导也采用高阶有限差分形式。

本发明进一步的改进在于，当δx＝δz时θ＝π/4，则差分方程简化为

利用差分方程进行波场迭代时，满足有限差分的稳定条件；以角度φ传播的平面波定义如下：

其中ω是角频率，是平面波的振幅；将上式带入差分方程，且只考虑最大波数，得到δt满足下面的稳定性条件：

与现有技术相比，本发明具有以下有益的效果：

(1)由于重力引起的岩石压实效应，地震波的传播速度通常会随着深度的增加而加快。基于这一事实，梯形坐标系设计可以耦合地下介质速度整体变化，该坐标系中均匀网格采样所对应的物理直角坐标系网格由浅入深逐渐增大，即浅部低速区对应细网格，深部高速区对应粗网格。因此，本发明在梯形坐标系下用有限差分求解波动方程，对应笛卡尔直角坐标系中为变网格有限差分，从而模拟地震波。

(2)本发明应用的梯形坐标系较直角坐标系更为一般，对应物理模型水平和深度方向采样间隔均随深度增加而增大，是一种变网格有限差分方法，且不会产生由于网格大小变化引起的虚假反射，能够有效减少传统固定网格有限差分对深部高速区域的过采样。

(3)本发明采用了卷积完美匹配层吸收边界条件来消除虚假的边界反射；

(4)本发明在计算效率上显著优于传统的固定网格有限差分算法，同时对电脑内存的需求大为降低。

附图说明

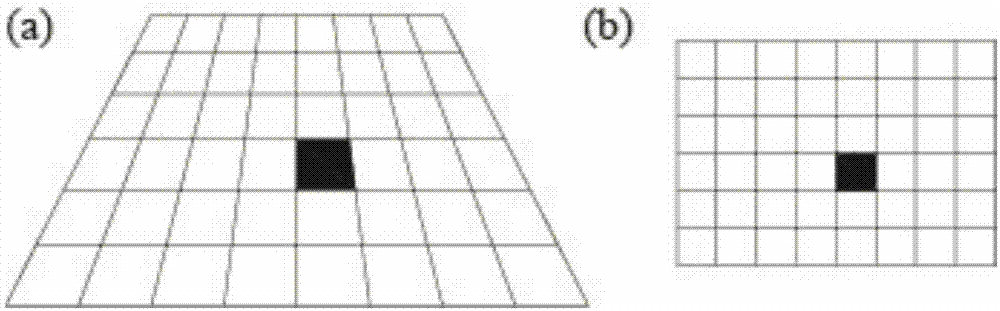
图1是直角坐标系和梯形坐标系的对应关系示意图，其中，(a)为直角坐标系下的梯形网格，(b)为梯形坐标系下的固定网格；图中黑色区域表示相同的采样位置。

图2是坐标变换中角度定义示意图。

图3是两层模型cpml边界条件下和无cpml边界条件下的波场快照：其中，(a)为带cpml边界条件，(b)为无cpml边界条件。黑色虚线表示两层的交界面，黑色五角星表示震源位置。

图4是marmousi速度模型：其中，(a)为地震波场模拟的实际区域，(b)为梯形坐标系marmousi模型，(c)为相应的纵向伸缩函数，(d)为纵向采样间隔从浅部到深部的变化图。

图5是marmousi模型模拟波场快照：其中，(a)为梯形坐标系下固定网格有限差分的波场快照，(b)为梯形坐标系波场((a)图)经坐标变换和插值到直角坐标系的波场快照，(c)为直角坐标系下传统固定网格有限差分的波场快照。

图6是marmousi模型波场快照在不同横向位置深度波形对比图：其中，(a)为3.5km，(b)为4.6875km，(c)为5.75km。实线和虚线分别表示传统和梯形坐标系固定网格有限差分的模拟结果。

具体实施方式

本发明针对地震波传播速度随深度逐渐增加这一普遍特征，提出一种二维梯形坐标系波动方程有限差分波场模拟方法，并采用了卷积完美匹配层吸收边界条件来消除虚假的边界反射。本发明基于卷积完美匹配层吸收边界，在梯形坐标系下用有限差分求解波动方程，实现一种物理横向和纵向网格采样间隔随深度增加的有限差分地震波模拟方法。首先确定梯形坐标系与直角坐标系下坐标位置之间的转换关系，然后推导卷积完美匹配层吸收边界条件下的二维波动方程在该梯形坐标系表达形式。最后，由于梯形坐标系波动方程出现空间混合偏导，本发明提出利用坐标变换将混合偏导化解为非混合偏导后，可利用常规均匀网格有限差分算法求解梯形坐标系下的波动方程，从而得到模拟波场。

下面结合附图和实例对本发明进行详细的描述。

本发明提出的一种基于卷积完美匹配层吸收边界的梯形网格有限差分地震波场正演模拟方法，其具体步骤如下：

(1)对给定的直角坐标系下的速度模型v(x0,z0)，确定梯形坐标系形状参数γ为：

式中，表示最深层的纵向深度坐标位置，是深度z0处的横向采样间隔，是深度z0处的最大横向采样间隔，是最深层最大横向采样间隔。其中，v^min(z0)是深度z0的最小速度，f0为震源主频率，ng为一个波长内采样点数。

(2)对给定的直角坐标系下的速度模型v(x0,z0)，进行坐标变换将其转换到梯形坐标系的速度模型v(x,z)，坐标变换表达式为：

式中，x和z分别是梯形坐标系下的横向与纵向坐标，α是梯形坐标横向位置参数，在地震波模拟时与震源横向位置相同，γ是梯形坐标系形状参数。纵向比例函数g(z)与速度有关，为使之后的有限差分有效进行，该函数必须是一阶和二阶连续的。在实际操作中，本发明利用三次样条插值来建立函数g(z)。

本发明中步骤(2)的具体过程如下：

采用如下的坐标变换将直角坐标系转换为梯形坐标系：

式中，(x0,z0)是直角坐标系坐标，(x,z)是梯形坐标系坐标。α是梯形坐标横向位置参数，在地震波模拟中一般与震源横向位置相同。γ是梯形坐标系形状参数，与模型速度随深度变化相关。纵向比例函数g(z)与速度有关，为使之后的有限差分有效进行，该函数必须为一阶和二阶连续。在本发明中，利用三次样条插值来建立函数g(z)。

若梯形坐标系下横向采样间隔为δx，则其对应物理直角坐标系采样间隔δx0和δz0可表示为

δx0(z)＝(1+γg(z))δx

δz0(z)＝g(z+δz)-g(z)

若直角坐标系下的速度模型v(x0,z0)中每个深度最小速度表示为v^min(z0)，且保持震源主频率下波数空间采样点数相同，则每个深度最大横向采样间隔可表示为

其中f0为震源主频率，ng为一个波长内采样点数，可根据对模拟精度需求设定。

其中，表示最深层最大横向采样间隔；那么，梯形坐标系形状参数γ可由如下表达式确定

图1所示为直角坐标系和梯形坐标系中对同一区域离散采样示意图。图1中(a)为直角坐标系一梯形区域，则在梯形坐标系下为一矩形区域(图1中(b))。二图中总采样点数相同，但图1中(a)中横向和纵向采样间隔随深度逐渐增大，而图1中(b)中为均匀采样。两个网格覆盖区域完全相同，黑色网格表示相同采样点。

(3)根据步骤(2)中的坐标变换，将直角坐标系(x0,z0)下的cpml(卷积完美匹配层吸收边界)条件下二维时域各向同性声波方程变换为梯形坐标系(x,z)下的声波方程：

式中，u＝u(x,z)是梯形坐标系下的压力场，t是时间，xs和zs分别是震源在梯形坐标系下的横纵坐标位置，f(t)是震源的时域波形函数，δ(·)表示狄拉克函数，辅助变量ψi和ζi(i∈{x,z})的定义如下：

式中j表示第j个时刻，系数ai和bi(i∈{x,z})表达式如下：

其中δt是时间间隔，r是理论边界反射系数，vmax是模型最大速度，li是cpml随着i变化的吸收厚度，是吸收区域到计算区域的距离，αmax＝πf0，其中f0是震源主频率。

步骤(3)的具体过程如下：

在给定的梯形坐标系与直角坐标系转换关系下，利用偏导数的求导规则，可将波场关于直角坐标系(x0,z0)的偏导转化为梯形坐标系(x,z)下的偏导。将直角坐标系压力场u(x0,z0)和梯形坐标系压力场u(x,z)分别简化为u0和u，则二者的一阶和二阶偏导关系为：

对于cpml边界条件下直角坐标系中的二维各向同性声波方程：

其中t为记录时间，δ(x)表示狄拉克函数，(x0s,z0s)是震源在直角坐标系中的横纵坐标，f(t)为时域震源函数，辅助变量和的结构如下：

在辅助变量的表达式中，j为第j个计算时刻，参数和表达式如下：

其中δt是时间间隔，r是理论边界反射系数，vmax是模型最大速度，是cpml随着i0变化的吸收厚度，是吸收区域到计算区域的距离，αmax＝πf0，其中f0是震源主频率。

那么根据两个坐标系间的偏导关系，对于上述cpml边界条件下直角坐标系中的二维各向同性声波方程，其在梯形坐标系下的声波方程为：

式中，u＝u(x,z)是梯形坐标系下的压力场，t是时间，xs和zs分别是震源在梯形坐标系下的横纵坐标位置，f(t)是时域震源函数，δ(·)表示狄拉克函数，辅助变量ψi和ζi(i∈{x,z})的结构如下：

系数ai和bi(i∈{x,z})表达式如下：

其中δt是时间间隔，r是理论边界反射系数，vmax是模型最大速度，li是卷积完美匹配层随着i变化的吸收厚度，是吸收区域到计算区域的距离，αmax＝πf0，其中f0是震源主频率。

(4)利用坐标变换，将步骤(3)中的梯形坐标系(x,z)下的声波方程转化为

其中坐标变换定义为：

其中(x',z')是变换后的坐标，θ为沿x方向的网格线与对角线的夹角，且满足0<θ<π/2。

步骤(4)的具体过程如下：

对于梯形坐标系中cpml边界条件下二维时域各向同性声波方程中出现的空间混合偏导项其较非空间混合偏导计算量大，可以通过坐标变换将其转换为二阶非混合偏导，如图2所示，定义如下的坐标变换：

式中，(x',z')是变换后的坐标，θ为沿x方向的网格线与对角线的夹角，且满足0<θ<π/2。那么，在此坐标变换下，混合偏导项可以表示为：

将此式代入梯形坐标系下的声波方程，得到最终用于波场模拟的声波方程为

(5)利用高阶有限差分对步骤(4)中的声波方程进行离散，得到cpml边界条件下梯形坐标系中的时间-空间域二维声波方程的差分方程，并利用此差分方程迭代求解，得到各个时刻的波场：

式中表示空间位置(xm,zn)＝(x+(m-1)δx,z+(n-1)δz)和第j个计算时刻点tj＝t0+(j-1)δt处的波场，δx和δz是梯形坐标系横向和纵向空间采样间隔，t0为震源时延。cp和ηp(p＝1,2,…,n)表示空间一阶和二阶偏导差分系数，n是对应于空间差分精度的差分点数。其中δt为时间采样间隔，需满足如下的稳定性条件：

步骤(5)的具体过程为：

对步骤(4)中得到的声波方程，为了提高模拟精度，空间偏导采用高阶有限差分格式：

其中表示空间位置(xm,zn)＝(x+(m-1)δx,z+(n-1)δz)和时刻tj＝t0+(j-1)δt处的波场，δx和δz是梯形坐标系横向和纵向空间采样间隔，δt为时间采样间隔，t0为震源时延。cp和ηp(p＝1,2,…,n)表示空间一阶和二阶偏导差分系数，n是对应于空间差分精度的差分点数。若梯形坐标系中横向和纵向空间采样间隔相同(即δx＝δz)，则坐标系(x',z')中采样有关系δx'²＝δz'²＝δx²+δz²，所以有

时间偏导数采用2阶，代入并化简后，则梯形坐标系中cpml边界条件下时间空间域二维声波方程差分方程为

式中，表示当且仅当m＝m0时，其他时候为0；同理。辅助变量ψi和ζi(i∈{x,z})及他们的偏导也采用高阶有限差分形式。

特别地，当δx＝δz时θ＝π/4，则差分方程可进一步简化为

利用上述差分方程进行波场迭代时，需要满足有限差分的稳定条件。以角度φ传播的平面波定义如下：

其中ω是角频率，是平面波的振幅。将上式带入差分方程，且只考虑最大波数(带奎斯特波数)，得到δt必须满足下面的稳定性条件：

数值仿真结果

下面给出不同速度模型的实验结果来验证本发明所提方法的有效性。首先在一个两层速度模型上展示了本算法的计算结果，随后在marmousi模型下进行数值运算，并与传统固定网格有限差分的结果进行比较。

数值实验1：两层速度模型数值模拟

该两层模型第一层速度为2000m/s，第二层速度为4000m/s，用主频为20hz的ricker子波为源放置在顶层正中间进行激发。横向采样间隔δx0从第一层的4m增加至最底层的16m(对应γ为2.4834*10^-4)。梯形坐标系下有限差分时间采样间隔为1.783ms。图3中(a)为采用卷积完美匹配层边界条件的波场快照，图3(b)为无cpml吸收边界条件下的波场快照。可以看出，采用cpml边界条件很好地避免了边界反射。

数值实验2：marmousi模型数值模拟

该原始模型横向和纵向采样点分别为256和425，横向采样间隔δx0为12.5m，纵向采样间隔δz0为4m，用主频为12hz的ricker子波为源放置在顶层正中间进行激发。梯形坐标系下有限差分时间采样间隔为1.404ms。图4中(a)展示了实际有限差分模拟区域，该区域在梯形坐标系下显示如图4(b)所示，相应的纵向比例函数如图4(c)所示。图4(d)表明实际的纵向采样间隔从第一层的8.333m增加至最底层的18.333m。图5中(a)展示了梯形坐标系下有限差分波场快照，图5(b)显示的是将图5(a)内插至与原始速度模型相同采样间隔波场。作为对比，图5(c)显示基于原始速度模型采样的固定网格传统有限差分相同时刻波场快照，与图5(b)相比二者整体上一致。图6展示了三个不同横向位置的深度域波形对比，虚线代表梯形网格有限差分的结果，实线代表常规固定网格有限差分的结果。图6中(a)、图6中(b)和图6中(c)分别距离震源3.5km、4.6875km和5.75km。可以看出这两种方法的结果是一致的。

本发明公开利用梯形坐标系可以耦合地下介质速度整体变化的优点，推导了梯形坐标系下波动方程的表达式并应用有限差分方法求解。数值算法上，采用常规均匀网格有限差分算法；而在物理上，则是对应变网格有限差分，即浅部低速区对应细网格，深部高速区对应粗网格，本发明可避免不同大小网格区域过渡所产生的虚假反射。此外，本发明采用卷积完美匹配层吸收边界条件来消除虚假的边界反射。与传统的固定网格有限差分算法相比，marmousi模型测试结果表明，本发明提出的方法快2.9倍，同时节省了80％的电脑内存。

本发明通过首先确定梯形坐标系坐标与直角坐标系坐标之间的转换关系，给出卷积完美匹配层吸收边界条件下的二维波动方程在该梯形坐标系表达形式。对于梯形坐标系波动方程中出现空间混合偏导，利用坐标变换将混合偏导化解为非混合偏导后求解梯形坐标系下的波动方程。本发明提出的方法可避免不同大小网格区域过渡所产生的虚假反射，能有效减少传统固定网格有限差分对深部高速区域的过采样。marmousi模型测试表明，与传统的固定网格有限差分算法相比，本发明提高有限差分地震波正演效率的同时可显著降低内存使用量。