一种最大协熵扩展椭球集员滤波方法与流程

本发明涉及机器人导航定位技术领域，特别是指一种最大协熵扩展椭球集员滤波方法。

背景技术：

集员滤波目的是根据提出的模型，噪声界和观测值来实时更新包含系统参数真值的参数可行集合(feasibleparameterset，fps)，这种方法用集合来替代传统的估计向量描述系统的滤波参数，任何处于参数可行集合内部的参数均可认为是可行的。集员滤波算法根据描述参数可行集合形状不同，可以分为椭球算法、多面体算法、盒子算法、全对称多胞形算法以及超平行提速拿法及区间算法等，它们分别采用对应的几何形状来近似描述各自的参数可行集合。

椭球集员滤波算法最早是由schweppe提出的，首次采用了椭球近似描述参数可行集合，并且在预测更新过程中给出了计算两椭球矢量和的运算法则，可以得到包含两椭球所有区域的外包椭球，在量测更新中，schweppe给出了计算两椭球交集的外包椭球计算方法，这两种计算法则确定了椭球集员滤波算法最根本的理论基础，但是其没有给出椭球的最优化计算法则，随后chernousko提出了预测更新中矢量和运算后外包椭球达到最小容积的条件公式，maksarov和norton提出了基于最小化椭球的体积以及椭球半轴长平方和的优化计算法则。盒子算法则由milanese和belforte提出来，其核心算法在于确定盒子的外定界，在线性系统中该问题可转化为线性规划问题，多面体算法目的是解决椭球与盒子算法中存在的不相容元素问题，可以精确描述参数可行集合，但是计算负担大，超平行体算法计算量较小，能够达到较高的估计精度；全对称多胞形算法能够精确无近似地表现出系统参数的时变特性。在椭球集员滤波算法中，fogel和huang提出了最小化椭球容积法则和最小化椭球迹法则。

技术实现要素：

针对现有中心差分滤波算法计算不稳定性的技术问题，本发明针对椭球集员滤波算法中噪声未知但有界假设基础上，机器学习理论中的信息熵理论思想，设计系统噪声预测误差和观测噪声误差的有界噪声项的最大协熵代价函数，从而构造出一种最大协熵扩展椭球集员滤波方法，并将其应用到自主移动机器人位姿模型中开展机器人系统状态空间模型状态参数计算中去，达到改善非线性集员滤波算法计算稳定性问题。

本发明的技术方案是这样实现的：

一种最大协熵扩展椭球集员滤波方法，其步骤如下：

步骤一、构建陆基自主移动机器人的非线性离散系统状态空间模型，并初始化非线性离散系统的系统状态变量，给出系统状态变量的椭球集合；其中，非线性离散系统状态空间模型包括动力学运动模型方程和离散化观测模型方程；

步骤二、根据非线性离散系统状态空间模型的初始化结果获得第k-1时刻的系统状态变量估计值和系统状态变量椭球形状矩阵pk-1，并对系统状态变量椭球形状矩阵pk-1进行cholesky分解操作；

步骤三、采用stirling插值多项式对第k-1时刻的系统状态变量估计值进行线性化逼近计算，并将线性化后的二阶多项式作为非线性离散系统的lagrange余子式；

步骤四、利用椭球将非线性离散系统的lagrange余子式外包得到线性化误差，并计算线性化误差的外包椭球；

步骤五、将线性化误差与非线性离散系统的过程噪声相加得到虚拟过程噪声误差，并计算虚拟过程噪声误差椭球，对虚拟过程噪声误差椭球进行实施cholesky分解操作；

步骤六、利用线性椭球集员滤波算法计算系统状态变量的状态参数椭球边界和系统状态变量预测值并根据虚拟过程噪声误差椭球预测系统状态变量的椭球形状矩阵；

步骤七、基于离散化观测模型方程和第k-1时刻的系统状态变量估计值对非线性离散系统的状态变量进行预测更新获得观测向量的预测值和预测椭球形状矩阵，并根据预测椭球形状矩阵的平方根和步骤六中的椭球形状矩阵的平方根计算预测协方差矩阵；

步骤八、根据步骤六中的系统状态变量预测值计算状态变量预测误差，并将步骤六中的系统状态变量预测值和观测方程相结合获得系统误差扩展方程；利用系统误差扩展方程的扩展噪声项构造的方差矩阵，根据方差矩阵获得转换扩展状态模型；

步骤九、根据步骤八的转换扩展状态模型，利用mcc准则构造代价函数，通过计算代价函数的最优解获得第k时刻的系统状态变量的最优估计值

步骤十、利用线性椭球集员滤波算法更新系统状态变量的状态参数椭球边界，根据状态参数椭球边界计算第k时刻的系统状态向量的预测值和预测方差矩阵。

所述非线性离散系统状态空间模型为：

其中，xk∈rⁿ表示k时刻的状态变量，xk-1表示k-1时刻的状态变量，f(·)和h(·)均表示非线性二阶可导函数，qk-1表示第k-1时刻的过程噪声项，rk∈r^m表示随时间变化的观测噪声项，yk表示观测向量；

所述系统状态变量的椭球集合为：

e(a，p)＝{x∈rⁿ|(x-a)^tp^-1(x-a)≤1}，

其中，a表示椭球集合的中心，p为正定性椭球包络矩阵，系统初始状态估计椭球集合为

所述采用stirling插值多项式对第k-1时刻的系统状态变量估计值进行线性化逼近计算的表达式为：

其中，xk表示k时刻的状态变量，dδx项称为差分算子；

其中，δxp表示系统状态变量解耦后的估计偏差量，μp为偏差算子，δp为平均算子，表示第k-1时刻的系统状态变量的估计偏差，s为插值步长；

所述偏差算子μp为：

所述平均算子δp为：

其中，为沿轴向的单位向量；

所述lagrange余子式为：

其中，表示以第k-1时刻的状态估计值为中心的lagrange余子项。

所述利用椭球将非线性离散系统的lagrange余子式外包得到线性化误差为：

其中，表示第k-1时刻由lagrange余子项确定的线性化误差形状矩阵的对角元，表示第k-1时刻由lagrange余子项确定的线性化误差形状矩阵的非对角元，i、j表示线性化误差形状矩阵的第i行第j列，取值为1≤i，j≤n，n为系统状态向量维数；

所述线性化误差的外包椭球为：其中，表示lagrange余子项确定的线性化误差形状矩阵。

所述虚拟过程噪声误差为：

其中，表示第k-1时刻的虚拟过程噪声，表示虚拟过程噪声方差矩阵，qk-1表示过程噪声矩阵，表示集合加操作，表示过程噪声误差优化因子；

所述虚拟过程噪声误差椭球为：其中，表示第k时刻的虚拟过程噪声；

对虚拟过程噪声误差椭球进行实施cholesky分解操作，得到：其中，表示虚拟过程噪声方差矩阵平方根。

所述系统状态变量预测值为：

其中为沿轴向的单位向量；

所述系统状态变量的椭球形状矩阵为：

其中，表示系统状态变量预测形状矩阵，表示p′k，k-1的平方根；

所述观测向量的预测值

其中，表示系统观测向量预测值；

预测协方差矩阵pxy，k，k-1为：

其中，表示系统观测方程预测误差矩阵；

所述状态变量预测误差为：

其中，表示状态变量预测误差；

所述系统误差扩展方程为：

其中，表示非线性观测方程的一阶差分算子矩阵，bk表示第k时刻的一阶差分算子矩阵，rk表示观测噪声项，i表示单位矩阵，是扩展噪声项；

所述利用系统误差扩展方程的扩展噪声项构造的方差矩阵为：

其中，θk表示扩展噪声方差阵，sk表示扩展噪声方差阵θk的cholesky分解矩阵，sr，k表示观测噪声误差矩阵的平方根，表示扩展噪声平方根矩阵；

所述转换扩展状态模型为：

dk＝wkxk+ek，

其中，表示第k时刻的扩展状态，表示第k时刻的扩展状态转移矩阵，且

所述代价函数为：

其中，di,k是矩阵dk的第i行向量，wi,k是矩阵wk的第i行向量，l＝n+m表示矩阵dk的维数，jl(xk)表示mcc代价函数，gσ表示误差代价函数；

所述第k时刻的系统状态变量的最优估计值为：

通过对代价函数的求偏导及整理可得：

其中，cx,k＝diag(gσ(d1,k-w1,kxk),…,gσ(dn,k-wn,kxk))，

cy,k＝diag(gσ(dn+1,k-wn+1,kxk),…,gσ(dn+m,k-wn+m,kxk))。

所述利用线性椭球集员滤波算法更新系统状态变量的状态参数椭球边界为：其中，pk表示第k时刻的系统状态变量估计误差矩阵，ek表示更新的系统状态变量椭球；

所述根据状态参数椭球边界计算第k时刻的系统状态向量的预测值为：

其中，表示椭球集员滤波器增益矩阵；

所述预测方差矩阵：

其中，ρk∈(0,1)，是观测方程的一阶差分算子矩阵。

本技术方案能产生的有益效果：本发明是在传统的基于最小均方误差准则的椭球集员滤波算法基础上，在观测更新步骤中引入新型的最大协熵mcc准则，通过非线性系统预测噪声误差与观测噪声联合实施系统模型扩展操作来获得新的系统噪声表达式，根据基于系统状态变量预测向量与观测向量间的最大协熵准则构造二阶信息势能公式表达的误差代价函数，从而设计出椭球集员滤波算法的观测更新计算过程，由此构造出一种新型的基于最大协熵的椭球集员滤波算法计算框架；利用本发明方法开展陆基机器人位姿计算仿真验证，本发明方法的计算精度获得改善，计算稳定性相比于传统椭球集员滤波算法得到明显改善和提高。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

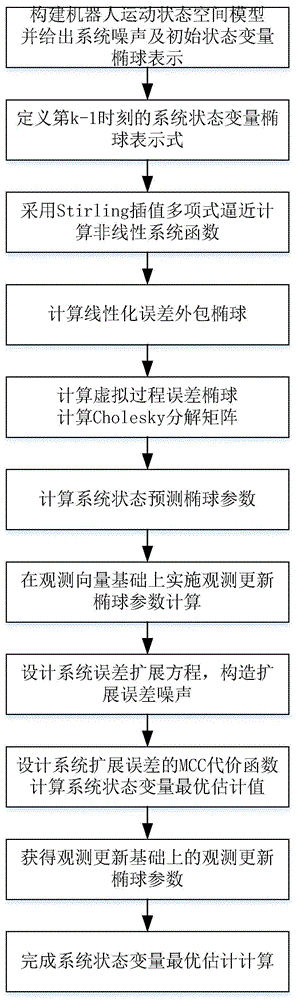
图1是本发明的计算流程图。

图2是本发明方法移动机器人运动模型示意图。

图3是本发明方法mcc-smf的移动机器人计算误差数据图。

图4是本发明方法mcc-smf的移动机器人载体轨迹计算数据图。

图5是ekf算法获得的移动机器人载体计算误差数据图。

图6是ekf算法获得的移动机器人载体轨迹计算数据图。

图7是sukf算法获得的移动机器人载体计算误差数据图。

图8是sukf算法获得的移动机器人载体轨迹计算数据图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

预备知识

协熵准则是一种局部相似度量概念，它定义核空间中两个随机向量间的相似度量，其优势在于对于较大误差的不敏感性，因此对于脉冲噪声或者异常数据处理不会对系统状态变量计算效能带来影响。针对两个随机变量x∈rⁿ，y∈rⁿ，其联合概率密度函数为px，y(x，y)，那么两个随机变量的协熵定义为，

协熵定义中的κ(x，y)是一个径向核函数，e[κ(x，y)]表示期望算子，径向核函数一般都是采用了高斯对称核函数表示的，

其中，x-y＝e表示两个变量向量的误差向量，σ表示核函数的带宽数值σ＞0；但是对于非对称高斯核分布，其核函数可表示为，

这里定义的σ+和σ-分别表示误差向量的“+”的和“-”的部分，那么非对称协熵可定义为，

对于有限数据集合可以采用简单的采样均值估计器逼近连续型高斯核函数的协熵表达式为，

进一步获得taylor级数扩展表达式为，

那么若考虑状态空间模型的状态参数x和输出变量y，基于最大协熵准则开展迭代递推最优滤波计算获得系统状态变量最优估计目标值可表示为，

那么可以利用最大协熵准则构造代价函数开展非线性系统状态空间模型状态参数滤波算法设计工作。

本发明针对中心差分滤波算法计算不稳定性，将其滤波计算准则从最小均方误差mmse修订为最大协熵准则mcc，从而设计获得一种新型的最大协商熵椭球集员滤波算法，并将其应用到自主移动机器人位姿模型中开展机器人系统状态空间模型状态参数计算中去。

本发明是在传统的基于最小均方误差准则的椭球集员滤波算法基础上，面向非线性系统状态空间模型，传统椭球集员滤波算法的时间更新预测步骤计算过程保留下来，在观测更新步骤中引入新型的最大协商熵mcc准则，通过非线性系统预测噪声误差与观测噪声联合实施系统模型扩展操作来获得新的系统噪声表达式，根据基于系统状态变量预测向量与观测向量间的最大协熵准则构造二阶信息势能公式表达的误差代价函数，从而设计出椭球集员滤波算法的观测更新计算过程，由此构造出一种新型的基于最大协熵的椭球集员滤波算法计算框架。利用本发明算法开展陆基机器人位姿计算仿真验证，本发明的计算精度获得改善，计算稳定性相比于传统椭球集员滤波算法得到明显改善和提高。

最大协熵准则是一种基于renyis熵公式计算误差信息最大值的方法，引入机器学习理论中的信息势能概念，抽象出二阶信息势能表达式描述椭球集员滤波算法中的非线性系统状态变量的预测误差，连同非线性系统状态空间模型的观测方程，获得非线性系统扩展误差状态模型，计算扩展误差状态模型的噪声方差，并对其进行cholesky分解获得扩展噪声的平方根方差正定矩阵，利用平方根噪声方差矩阵对扩展误差状态模型进行变换整理获得预测误差与观测噪声联合误差表达式，进而利用最大协商熵准则的二阶信息势能表达式综合出椭球集员滤波算法的预测误差代价函数，那么利用最大协商熵代价函数最小化来获得系统状态变量的最优化计算，具体做法就是对最小化误差熵代价函数计算偏微分并令其为0来获得，同时利用矩阵逆定理实现系统状态变量最优化计算显性表达式，并且在计算机算法编制中设置一个小量参数对每一次迭代计算的系统状态变量估计值进行判断，若判断表达式成立，则继续进行系统状态变量估计方差矩阵计算；否则的话继续进行前面步骤的计算过程，最后获得系统状态变量估计方差矩阵的计算。

如图1所示，本发明实施例提供了一种最大协熵扩展椭球集员滤波方法，其步骤如下：

步骤一、构建陆基自主移动机器人的非线性离散系统状态空间模型，并初始化非线性离散系统的系统状态变量，给出系统状态变量的椭球集合；其中，非线性离散系统状态空间模型包括动力学运动模型方程和离散化观测模型方程；

所述非线性离散系统状态空间模型为：

其中，xk∈rⁿ表示k时刻的状态变量，xk-1表示k-1时刻的状态变量，f(·)和h(·)均表示非线性二阶可导函数，qk-1表示第k-1时刻的过程噪声项，rk∈r^m表示随时间变化的观测噪声项，yk表示观测向量；qk-1∈rⁿ和rk∈r^m表示随时间变化的过程噪声和观测噪声，并且满足未知但有界(ubb)假设条件，记qk∈(0，qk)和rk∈(0，rk)。系统的初始状态x0属于一个已知的有界集合x0∈x0，该集合可以由系统状态的先验知识确定，同时对于测量序列向量那么k时刻的椭球集员滤波算法的状态可行集合定义为xk，它由所有可能的状态点组成，这些状态点与所有可获取的信息，包括系统模型、噪声假设和初始状态集合相一致。

所述系统状态变量的椭球集合为：

e(a，p)＝{x∈rⁿ|(x-a)^tp^-1(x-a)≤1}(9)，

其中，a表示椭球集合的中心，p为正定性椭球包络矩阵，系统初始状态估计椭球集合为k-1时刻估计得到的系统状态椭球集合为则k时刻非线性椭球集员滤波算法的迭代过程由步骤二至步骤八组成。

步骤二、根据非线性离散系统状态空间模型的初始化结果获得第k-1时刻的系统状态变量估计值和系统状态变量椭球形状矩阵pk-1，并对系统状态变量椭球形状矩阵pk-1进行cholesky分解操作，设置k-1时刻状态分量的不确定区间为，

其中，i＝1，2，...，n，表示sk-1第(i，i)个对角元素。

步骤三、在非线性系统状态空间模型设计过程中，对于运动目标的非线性系统函数实施线性化逼近计算，这里采用stirling插值多项式开展非线性函数的线性化逼近计算，采用stirling插值多项式对第k-1时刻的系统状态变量估计值进行线性化逼近计算，并将线性化后的二阶多项式作为非线性离散系统的lagrange余子式；

所述采用stirling插值多项式对第k-1时刻的系统状态变量估计值进行线性化逼近计算的表达式为：

其中，xk表示k时刻的状态变量，dδx项称为差分算子；

其中，δxp表示系统状态变量解耦后的估计偏差量，μp为偏差算子，δp为平均算子，表示第k-1时刻的系统状态变量的估计偏差，s为插值步长；

所述偏差算子μp为：

所述平均算子δp为：

其中，为沿轴向的单位向量；

从stirling插值多项式逼近表达式可以看出，stirling插值展开式的计算精度高于taylor级数展开式，且其精度可由插值步长s来控制。取stirling插值多项式的前两项作为非线性系统过程函数的线性化近似，所述lagrange余子式为：

其中，表示以第k-1时刻的状态估计值为中心的lagrange余子项。

步骤四、利用椭球将非线性离散系统的lagrange余子式外包得到线性化误差，并计算线性化误差的外包椭球；

所述利用椭球将非线性离散系统的lagrange余子式外包得到线性化误差为：

其中，表示第k-1时刻由lagrange余子项确定的线性化误差形状矩阵的对角元，表示第k-1时刻由lagrange余子项确定的线性化误差形状矩阵的非对角元，i、j表示线性化误差形状矩阵的第i行第j列，取值为1≤i，j≤n，n为系统状态向量维数；

所述线性化误差的外包椭球为：其中表示lagrange余子项确定的线性化误差形状矩阵。。

步骤五、将线性化误差与非线性离散系统的过程噪声相加得到虚拟过程噪声误差，并计算虚拟过程噪声误差椭球，对虚拟过程噪声误差椭球进行实施cholesky分解操作；

所述虚拟过程噪声误差为：

其中，表示第k-1时刻的虚拟过程噪声，表示虚拟过程噪声方差矩阵，qk-1表示过程噪声矩阵，表示集合加操作，表示过程噪声误差优化因子；

所述虚拟过程噪声误差椭球为：其中，表示第k时刻的虚拟过程噪声；

对虚拟过程噪声误差椭球进行实施cholesky分解操作，得到：其中，表示虚拟过程噪声方差矩阵平方根。

步骤六、利用线性椭球集员滤波算法计算系统状态变量的状态参数椭球边界和系统状态变量预测值并根据虚拟过程噪声误差椭球预测系统状态变量的椭球形状矩阵；利用线性椭球集员滤波算法的预测步骤计算预测状态参数椭球边界，这是线性化预测椭球和虚拟过程噪声直和计算过程；

所述系统状态变量预测值为：

其中为沿轴向的单位向量；

所述系统状态变量的椭球形状矩阵为：

其中，表示系统状态变量预测形状矩阵，表示p′k，k-1的平方根；

步骤七、基于离散化观测模型方程和第k-1时刻的系统状态变量估计值对非线性离散系统的状态变量进行预测更新获得观测向量的预测值和预测椭球形状矩阵，并根据预测椭球形状矩阵的平方根和步骤六中的椭球形状矩阵的平方根计算预测协方差矩阵；

在对非线性系统状态变量做出预测更新基础上对观测向量做出一步预测，所得观测向量的预测值为：

其中，表示系统观测向量预测值；

预测协方差矩阵pxy，k，k-1为：

其中，表示系统观测方程预测误差矩阵；

步骤八、根据步骤六中的系统状态变量预测值计算状态变量预测误差，并将步骤六中的系统状态变量预测值和观测方程相结合获得系统误差扩展方程；利用系统误差扩展方程的扩展噪声项构造的方差矩阵，根据方差矩阵获得转换扩展状态模型；

所述状态变量预测误差为：

其中，表示状态变量预测误差；

所述系统误差扩展方程为：

其中，表示非线性观测方程的一阶差分算子矩阵，bk表示第k时刻的一阶差分算子矩阵，rk表示观测噪声项，i表示单位矩阵，是扩展噪声项；

所述利用系统误差扩展方程的扩展噪声项构造的方差矩阵为：

其中，θk表示扩展噪声方差阵，sk表示扩展噪声方差阵θk的cholesky分解矩阵，sr，k表示观测噪声误差矩阵的平方根，表示扩展噪声平方根矩阵；；

所述转换扩展状态模型为：

dk＝wkxk+ek(30)，

其中，表示第k时刻的扩展状态，表示第k时刻的扩展状态转移矩阵，且

步骤九、根据步骤八的转换扩展状态模型，利用mcc准则构造代价函数，通过计算代价函数的最优解获得第k时刻的系统状态变量的最优估计值

所述代价函数为：

其中，di，k是矩阵dk的第i行向量，wi，k是矩阵wk的第i行向量，l＝n+m表示矩阵dk的维数，jl(xk)表示mcc代价函数，gσ表示误差代价函数；；

系统状态变量的最优估计值是式(31)的最优解，因此，述第k时刻的系统状态变量的最优估计值为：

通过对式(31)求解偏微分获得表达式为，

进一步整理可得：

其中，cx，k＝diag(gσ(d1，k-w1，kxk)，…，gσ(dn，k-wn，kxk))，

cy，k＝diag(gσ(dn+1，k-wn+1，kxk)，…，gσ(dn+m，k-wn+m，kxk))。

步骤十、利用线性椭球集员滤波算法更新系统状态变量的状态参数椭球边界其中，pk表示第k时刻的系统状态变量估计误差矩阵，ek表示更新的系统状态变量椭球；其实质是将预测状态椭球和观测集合做直和交集计算，

根据状态参数椭球边界计算第k时刻的系统状态向量的预测值和预测方差矩阵，

所述预测方差矩阵：

其中，是观测方程的一阶差分算子矩阵。

本发明的优势在于采用stirling插值多项式实施线性化操作，有效避免taylor级数展开式的一阶jacobian矩阵和二阶hessian矩阵的复杂计算，降低了算法计算复杂度；利用插值步长s能够控制计算精度；相比于taylor级数扩展的传统非线性集员滤波算法，本发明方法的计算精度比较高。

另外本算法中引入了四个参数，插值步长s和三个尺度因子参数βk-1和ρk，其数值确定方法如下：

对于插值步长s参数，一般情况下若系统状态向量满足gauss分布时，为了满足这一条件，每次迭代计算的系统状态向量的估计方差矩阵都实施cholsky分解，p＝ss^t，从而对系统状态向量开展解耦变换操作，使其满足gauss分布条件。

尺度因子参数和βk-1涉及到两个椭球直和运算的外包椭球最优化问题，这里选取外包椭球迹最小化计算方法，该方法求解形式简单，相比较于最小化外包椭球体积的优化准则，该方法性能鲁棒性更强。即有从而可以采用式子获得最优的尺度因子参数和βk-1。

尺度因子参数需要e(0，qk-1)和直和计算，那么其计算准则式为：

其最优计算式为

对于尺度因子参数βk-1，需要两个椭球和的直和计算，考虑观测向量更新条件下的方差矩阵计算式为：

从而可以得到尺度因子参数βk-1的计算公式为

在迭代计算过程中，观测集合sy形式一般都比较复杂，从而导致系统状态向量方差矩阵pk的计算复杂性，无论采用最小化椭球体积法还是最小化椭球迹准则，都使尺度因子参数ρk的优化计算很困难，甚至无法获得解析解，若采用数值计算方法的话计算复杂度很高。在本发明中采用最小化性能指标δk上界形式来计算

这样可以获得尺度因子参数ρk的一种次优计算式

其中pm是矩阵的最大奇异值，cm是矩阵的最大奇异值。

应用实例

为了验证本发明提出的最小误差熵中心差分滤波算法的计算效能，利用本发明方法对陆基机器人定位系统模型开展仿真验证计算，来证明本发明方法的有效性及其计算优势，这里给出仿真验证测试数据。这里考虑一个地面移动机器人系统，它采用前轮驱动模式，如图2所示，定义前轮转向角为α，以逆时针方向为正方向，机器人坐标系xyrobot相对于地面坐标系xyground的转向角度为ψ，以逆时针方向为正，后轮速度定义为vrearwheel。从几何图形可以看出观测点到后轮中心的距离r和前后轮轴距l之间满足

从而可以获得观测点距离，同时可以得到后轮速度表达式为：可以整理获得机器人转向角方程为，

整理获得

若再考虑机动机器人系统的运动速度，可以在机器人坐标系中得到机动机器人系统的动力学方程为

把机器人系统动力学方程转换到地面坐标系中，可以获得最终的地面坐标系中的移动机器人系统移动方程

系统方程中的参数α(t)可作为调制参数，作为系统的输入变量，产生一个前轮的控制参数，其满足控制律

这里的参数ψdes表示期望的航向角，参数ψ表示当前的运动航向角，那么期望得到的航向角可以表达为

一般来说转向角的范围在(±π/4)内，g参数影响着机器人转向的速率快慢。对于移动机器人系统运动方程目的是开展系统状态变量估计和运动路径跟踪，因此有很多传感器来感知系统坐标位置，如gps或者正向编码测向仪等设备来完成目标跟踪观测，这里选择在地面坐标系中的移动机器人的两向位置坐标作为观测变量，因此观测方程是线性的，可以直接获得的。考虑系统初始方差矩阵为

另外系统参数设置为移动机器人前后轮轴距l＝2m，控制律增益g＝2，移动速度保持为v＝1m/s，采样时间间隔δt＝0.1s；假设过程变量中仅有航向角ψ有干扰噪声，可设过程噪声方差为q＝0.05²。观测变量是移动机器人位置坐标，因此观测噪声方差矩阵可设为

从而可以获得移动机器人系统的移动轨迹仿真结果，这里本发明方法、ekf算法、sukf算法，其结果如图3-图8所示。利用ekf算法和sukf算法对本发明mcc-smf算法进行比较，可以看到，mcc-smf算法的计算稳定性比较好，且其计算收敛速度快，计算精度获得明显改善与提高。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。