一种用于轮胎魔术公式的参数辨识及优化方法与流程

本发明属于车辆动力学参数辨识技术领域，涉及一种用于轮胎魔术公式的参数辨识及优化方法。

背景技术：

随着汽车产业的迅速壮大以及市场汽车保有量的大幅提高，同时车辆技术和计算机信息技术的快速发展，无论是对于传统汽车还是新能源汽车，车辆设计越来越偏向低成本高效化、信息化等，信息技术推动着现代汽车设计技术的发展，加工制造的智能化、精细化以及快速化，提高了汽车制造技术的科技含量，使传统的制造技术发生质的改变。特别是计算机仿真技术在汽车工业中的应用，极大方便了产品的设计研发，提高了产品的质量，给汽车企业以及相关科研机构提供有效的帮助。汽车仿真分析技术可对汽车产品的性能及其可制造性进行预测和分析，从而缩短产品的设计与制造周期，降低产品的开发成本，提高研发设计系统快速响应市场变化的能力。

轮胎是车辆与道路保持直接接触的唯一的关键部件，是汽车的重要组成部分，作为汽车与道路面的支承和传递单元，它的力学特性是研究汽车动力学的基础。轮胎所受到的纵向力、侧向力、垂直载荷以及回正力矩对车辆的动力性、操纵稳定性、制动稳定性、乘坐舒适性以及行驶安全性起重要作用。建立合理的轮胎动力学模型对产品的开发和车辆整车性能分析有关键作用，所以轮胎模型的精度可直接接影响到汽车产品的后续研究中。

魔术公式轮胎模型是一种基于试验数据得到的经验型模型公式，可以准确的描述轮胎的侧偏性能，被广泛应用与车辆动力学的研究中。魔术公式是基于轮胎试验数据，用三角函数的组合拟合得到的公式，这一系列形式相同的公式可完整地表达轮胎所受纵向力、侧向力、回正力矩、翻转力矩，以及阻力矩分别和纵向力、侧向力的联合作用工况。

魔术公式的一般表达式为：

Y(x)＝Dsin(Carctan(Bx-E(Bx-arctan(Bx))))+……

其中Y(x)可以是侧向力，也可以是回正力矩或纵向力，x可以在不同工况下分别表示轮胎的侧偏角或纵向滑移率，公式的系数B、C、D、E等由轮胎的垂直载荷和外倾角确定。可见魔术公式参数多，高度非线性化，所以对其中参数的辨识显得较为困难但尤为重要。目前，对于一般的魔术公式参数辨识问题多采用遗传算法进行研究，遗传算法虽然也可进行辨识，可以在全局范围内逼近最优解，但局部搜索能力较差，收敛速度较慢，算法实时性欠佳。

技术实现要素：

本发明的目的在于克服现有技术的不足之处，提出一种用于轮胎魔术公式的参数辨识及优化方法。该方法目的性强，收敛速度非常快，并且求解精度高。

为了使用实际测量数据拟合出魔术公式中的参数并进行优化，本发明采用以下技术方案：

一种用于轮胎魔术公式的参数辨识及优化方法，包括以下步骤：

1)按照汽车轮胎动力学试验进行试验操作，基于经验型魔术公式轮胎模型，针对不同工况采集公式中相应的自变量与因变量的数据；

2)将步骤1)所采集得到的数据通过非线性最小二乘法先初次辨识轮胎魔术公式中的主要参数；

3)在步骤2)的基础上运用粒子群算法对初次辨识得到的参数进行深度优化，实现魔术公式参数的自适应调整，得到优化后的辨识参数值。

作为本发明的进一步改进，步骤1)具体为：对轮胎进行不同工况下相应力学特性的试验，通过试验中传感器检测并采集得各工况下轮胎模型魔术公式中的Y(x)和x数据，包括侧向力、回正力矩或纵向力，以及不同工况下分别对应的轮胎的侧偏角或纵向滑移率。

作为本发明的进一步改进，步骤2)中的非线性最小二乘法是通过泰勒级数将公式展开为线性模型，其包括一阶展开式，高阶展开式均归入误差项，然后再进行最小二乘回归，将得到的估计量作为新的展开点，再对线性部分进行估计，如此往复迭代，直至收敛。

作为本发明的进一步改进，步骤3)中的粒子群算法是指首先在可行解的范围内初始化一群粒子，每个粒子代表一个解；用位置和速度来表示该粒子的特征，引入适应度函数来计算粒子的适应度值来表示粒子的优劣；在解的空间内，通过跟踪个体极值和群体极值来更新个体位置；粒子每更新一次位置，就重新计算一次适应度值，通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值和群体极值的位置；

其中，个体极值是指个体所经历位置中适应度值最优位置，群体极值是种群中所有粒子搜索到的适应度最优位置。

作为本发明的进一步改进，粒子群算法得具体步骤如下：

3.1)进行初始化，设置粒子群算法中初始化因子；

3.2)粒子适应度值计算；

3.3)在每次迭代过程中，粒子通过搜索个体极值和群体极值进行粒子的速度更新和位置更新；

3.4)不断更新粒子速度和位置，并且根据新粒子的适应度值更新个体极值和群体极值；同时根据初始化中设定的迭代次数阈值和设定的循环条件进行循环；

若迭代次数达到阈值则迭代结束，否则转入步骤3.3)，依次循环更新各粒子的速度和位置，最后得到优化后参数值。

作为本发明的进一步改进，步骤2)具体算法如下：

设模型中存在(k+1)个参数β＝(β₀,β₁,K,β_k)；

首先选择一组初值：β₀＝(β_0,0,β_1,0,K,β_k,0)，将f(X,β)在β₀点展开，可以得到：

f(X,β)＝f(X,β₀)+g₍₀₎′(β-β₍₀₎)+R

其中g₍₀₎表示一阶导数在β₀＝(β_0,0,β_1,0,K,β_k,0)时取值，R为高阶部分，但只保留β的线性部分，将高阶部分归入误差项，可以得到：

y＝f(X,β)+u＝f(X,β₀)+g₍₀₎′(β-β₍₀₎)+R+u

＝g₍₀₎′β+f(X,β₀)-g₍₀₎′β+u₁

其中，随机扰动项u₁包含u和泰勒级数展开式中的高阶部分，得到新的回归模型：

y-f(X,β₀)+g₍₀₎′β₍₀₎＝g₍₀₎′β+u

新的目标函数为模型的最小二乘估计量为:

β₁＝(g₍₀₎g₍₀₎′)^-1g₍₀₎(y-f(X,β₀)+g₍₀₎′β₍₀₎)

＝β₍₀₎+(g₍₀₎g₍₀₎′)g₍₀₎(y-f(X,β₍₀₎))

因此非线性最小二乘迭代估计式为：

β_j+1＝β_(j)+(g_(j)g_(j)′)g_(j)(y-f(X,β_(j)))。

作为本发明的进一步改进，步骤3.1)根据需要辨识的魔术公式轮胎模型对粒子种群进行初始化：

在一个D维的搜索空间中，由n个粒子组成的种群X＝(X₁,X₂,L,X_n)；其中需要设置的参数有粒子群内粒子数目n、加速度因子c₁、c₂、惯重权数ω和迭代次数k；

其中，第i个粒子表示为一个D维的向量X_i＝(X_i1,X_i2,L,X_iD)^T，代表第i个粒子在D维搜索空间中的位置，也代表模型的一个潜在解；

粒子初始位置参考非线性最小二乘法得到的参数进行初始化。

作为本发明的进一步改进，步骤3.2)具体步骤如下：

根据目标函数计算出每个粒子位置X_i对应的适应度值，第i个粒子的速度为：

V_i＝(V_i1,V_i2,L,V_iD)^T，

其个体极值为P_i＝(P_i1,P_i2,L,P_iD)^T，种群的群体极值为P_g＝(P_g1,P_g2,L,P_gD)^T；

对于一般魔术公式，设置适应度函数如下：

Y(x)＝Dsin(Carctan(Bx-E(Bx-arctan(Bx))))+……

其中，x为方程输入，Y(x)为方程输出，B、C、D、E为待拟合的参数；

根据步骤2)得到的魔术公式的参数通过粒子群计算可以得出：

Y(x_j)＝D_isin(C_iarctan(B_ix_j-E_i(B_ix_j-arctan(B_ix_j))))+……

其中，D_i、C_i、B_i、E_i等表示步骤2)得到的参数值，x_j表示方程第j个输入值，Y(x_j)表示方程输出值；结合试验数据引入目标函数是每一次优化辨识结果的参数所拟合函数的输出值与实际测量值之差的均方根：

$\sqrt{\frac{1}{N}\underset{i=1}{\overset{n}{\Σ}}\{{\[\left(D_{i}sin\right(C_i\arctan \left(B_i{x}_j-E_i\left(B_i{x}_j-\arctan \left(B_i{x}_j\right)\right)\right))+\mathrm{......}\]-Y\left(x_j\right)\}}^2}$

其中，n为试验数据的个数，B_i,C_iD_i,E_iL为第i次搜索所对应的参数，x_j,Y(x_j)分别为第j次试验数据的测试结果。

作为本发明的进一步改进，步骤3.3)中，

速度更新公式为：V_id(k+1)＝ω×V_id(k)+c₁r₁×[P_id(k)-X_id(k)]+c₂r₂×[P_gd(k)-X_gd(k)]；

位置更新公式为：X_id(k+1)＝X_id(k)+V_id(k+1)；

其中，ω为惯重权数，d＝1,2,L,D；i＝1,2,L,n；k为当前的迭代次数；表示编号为id的的粒子当前迭代次数为k的速度；表示编号为id的例子当前迭代次数为k的位置；表示当前迭代次数为k时第d个种群的极值；c₁、c₂是非负的常数，称成为加速度因子；r₁和r₂是分布于[0,1]区间的随机数。

与现有参数辨识技术相比，本发明提供的方法具有以下优点：

本发明的方法在轮胎动力学模型基础上，通过试验测试采集得到所需数据，然后基于经验型魔术公式轮胎模型，首先采用非线性最小二乘法对数据进行拟合，通过迭代对魔术公式参数进行初次辨识。然后利用粒子群优化算法，根据魔术公式的特点，确定适应度函数，通过粒子群算法辨识，进行参数的辨识及其优化，能够得到科学合理的公式参数值。该方法目的性强，收敛速度非常快，并且求解精度高。能够实现对常用的轮胎魔术公式中的参数进行辨识及其优化，所得到的参数辨识值可用于计算和分析轮胎在其他工况下的受力情况以及车辆的产品设计等方面。具体优点为：

1)将非线性最小二乘拟合与粒子群算法相结合，首选用非线性最小二乘方法对采样数据进行初次辨识，再用粒子群优化算法对初次辨识结果进行优化再辨识，与一般辨识采用的遗传算法不同，遗传算虽可以在全局范围内逼近最优解，但局部搜索能力较差，收敛速度较慢，算法实时性欠佳。

2)该发明采用的粒子群优化算法具有以下优点：该算法规则简单，目的性强；收敛速度非常快，同时有很多措施可以避免陷入局部最优，从而求得全局最优；求解精度高，容易实现。

附图说明

图1是本发明提供的轮胎魔术公式的参数辨识及优化方法总流程图；

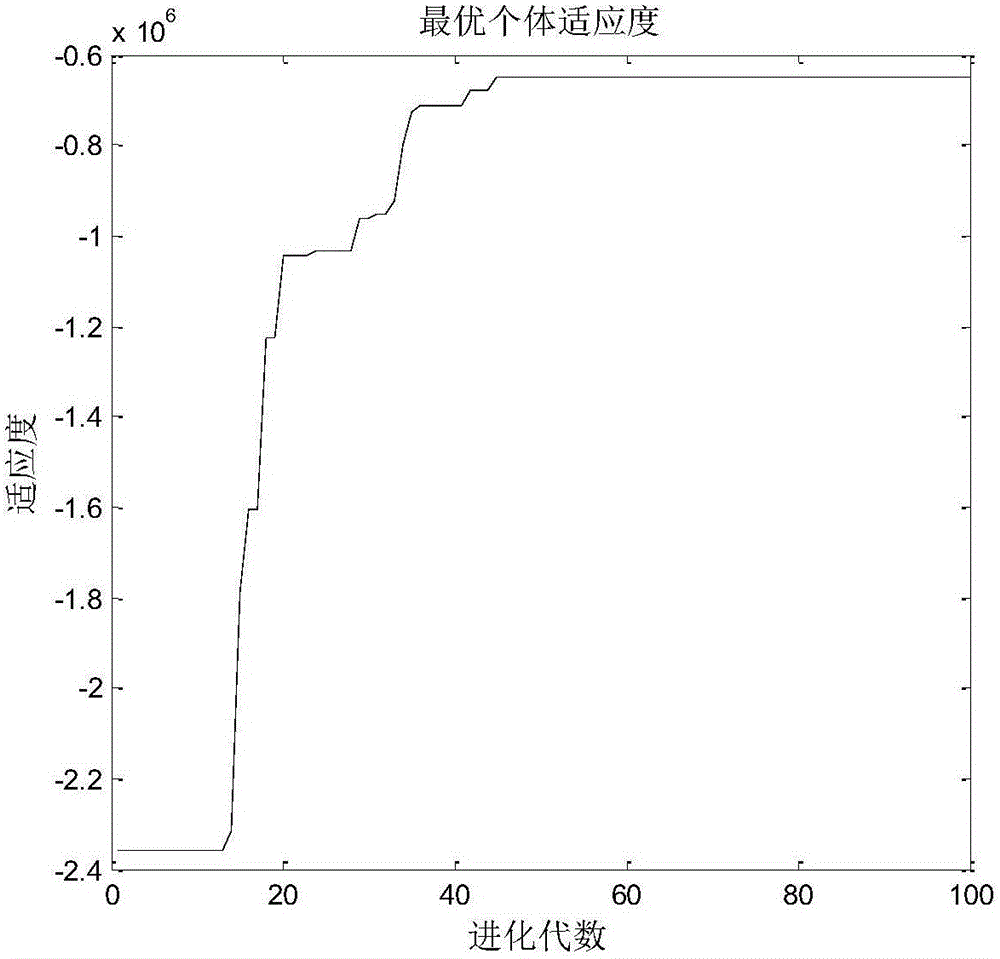
图2是本发明提供的具体实施方式中在参数辨识过程中粒子群适应度值的变化曲线；

图3是本发明提供的具体实施方式中使用粒子群算法优化之后与优化之前的对比曲线。

具体实施方式

如图1所示，本发明一种用于轮胎魔术公式的参数辨识及优化方法，在轮胎动力学模型基础上，基于简化后的经验型魔术公式轮胎模型，利用最小二乘方法初步识别出简化后的魔术公式中的参数，为更加精准地辨识魔术公式参数，进一步确定各参数可能取值范围，利用粒子群算法对初次识别得到的一系列参数进行优化，实现魔术公式参数的自适应调整，最终辨识得到准确度高、精确性好的魔术公式参数，进而为车辆整车性能的分析以及后续产品研究做好基础。

其特征具体包括以下步骤：

步骤一：轮胎模型魔术公式中的数据采样。

对轮胎进行不同工况下相应力学特性的试验，通过试验中传感器检测并采集得各工况下轮胎模型魔术公式中的Y(x)和x数据。如侧向力、回正力矩或纵向力，以及不同工况下分别对应的轮胎的侧偏角或纵向滑移率等。

步骤二：采用非线性最小二乘方法先初次辨识轮胎魔术公式中的主要参数。主要是通过对步骤一中采样到的数据进行非线性最小二乘拟合，经过数据拟合，初次辨识得到魔术公式中的参数值。

非线性最小二乘的具体方法是通过泰勒级数将公式展开为线性模型，即只包括一阶展开式，而高阶展开式均归入误差项，然后再进行最小二乘回归，将得到的估计量作为新的展开点，再对线性部分进行估计。如此往复迭代，直至收敛。具体算法设计如下：

设模型中存在(k+1)个参数β＝(β₀,β₁,K,β_k)。

首先选择一组初值：

β₀＝(β_0,0,β_1,0,K,β_k,0)，将f(X,β)在β₀点展开，可以得到：

f(X,β)＝f(X,β₀)+g₍₀₎′(β-β₍₀₎)+R

其中g₍₀₎表示一阶导数在β₀＝(β_0,0,β_1,0,K,β_k,0)时取值，R为高阶部分，但只保留β的线性部分，将高阶部分归入误差项，可以得到：

y＝f(X,β)+u＝f(X,β₀)+g₍₀₎′(β-β₍₀₎)+R+u

＝g₍₀₎′β+f(X,β₀)-g₍₀₎′β+u₁

其中，随机扰动项u₁包含u和泰勒级数展开式中的高阶部分，得到新的回归模型：

y-f(X,β₀)+g₍₀₎′β₍₀₎＝g₍₀₎′β+u

新的目标函数为模型的最小二乘估计量

为:

因此非线性最小二乘迭代估计式为：

β_j+1＝β_(j)+(g_(j)g_(j)′)g_(j)(y-f(X,β_(j)))

易知，由非线性最小二乘法算法流程可以看出如果要得到较好的结果需要设置较好的初始值与迭代结束法则。因此由非线性最小二乘法拟合得到的参数虽然是较为符合的参数，但不一定是最优的参数，还存在可以继续优化的空间。为了更加精确的辨识魔术公式的参数，我们提出采用粒子群算法对非线性最小二乘法辨识得到的参数结果进行再优化。

步骤三：通过步骤二获得魔术公式初次辨识的参数后，采用基本粒子群算法对魔术公式的参数进行再次辨识以及优化，以得到更精确的结果。

粒子群算法首先在可行解的范围内初始化一群粒子，每个粒子代表一个解。用位置和速度来表示该粒子的特征，引入适应度函数来计算粒子的适应度值来表示粒子的优劣。在解的空间内，通过跟踪个体极值和群体极值来更新个体位置。个体极值是指个体所经历位置中适应度值最优位置，群体极值是种群中所有粒子搜索到的适应度最优位置。粒子每更新一次位置，就重新计算一次适应度值，通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值和群体极值的位置。

步骤3.1：进行初始化，设置粒子群算法中初始化因子。

其中需要设置的参数有粒子群内粒子数目n、加速度因子c₁、c₂、惯重权数ω和迭代次数k。

假设在一个D维的搜索空间中，由n个粒子组成的种群X＝(X₁,X₂,L,X_n)

其中第i个粒子表示为一个D维的向量X_i＝(X_i1,X_i2,L,X_iD)^T，代表第i个粒子在D维搜索空间中的位置，也代表模型的一个潜在解。

优化算法的粒子初始位置参考非线性最小二乘法得到的参数进行初始化。

步骤3.2：粒子适应度值计算。

根据目标函数即可计算出每个粒子位置X_i对应的适应度值，

第i个粒子的速度为V_i＝(V_i1,V_i2,L,V_iD)^T，

其个体极值为P_i＝(P_i1,P_i2,L,P_iD)^T，

种群的群体极值为：P_g＝(P_g1,P_g2,L,P_gD)^T。

对于一般魔术公式，设置适应度函数如下，即待辨识的模型：

Y(x)＝Dsin(Carctan(Bx-E(Bx-arctan(Bx))))+……

其中x为方程输入，Y(x)为方程输出，B、C、D、E等为待拟合的参数

根据步骤二得到的魔术公式的参数(B、C、D、E等)通过粒子群计算可以得出：

Y(x_j)＝D_isin(C_iarctan(B_ix_j-E_i(B_ix_j-arctan(B_ix_j))))+……

其中的D_i、C_i、B_i、E_i等表示步骤二得到的参数值，x_j表示方程第j个输入值，Y(x_j)表示方程输出值。结合试验数据可以引入目标函数是每一次优化辨识结果的参数所拟合函数的输出值与实际测量值之差的均方根：

$\sqrt{\frac{1}{N}\underset{i=1}{\overset{n}{\Σ}}\{{\[\left(D_{i}sin\right(C_i\arctan \left(B_i{x}_j-E_i\left(B_i{x}_j-\arctan \left(B_i{x}_j\right)\right)\right))+\mathrm{......}\]-Y\left(x_j\right)\}}^2}$

其中n为试验数据的个数，B_i,C_iD_i,E_i L为第i次搜索所对应的参数，x_j,Y(x_j)分别为第j次试验数据的测试结果。

步骤3.3：在每次迭代过程中，粒子通过搜索个体极值和群体极值进行粒子的速度更新和位置更新，其中粒子群算法公式中更新粒子的位置和速度公式：

速度更新公式：V_id(k+1)＝ω×V_id(k)+c₁r₁×[P_id(k)-X_id(k)]+c₂r₂×[P_gd(k)-X_gd(k)]

位置更新公式：

X_id(k+1)＝X_id(k)+V_id(k+1)

其中ω为惯重权数，d＝1,2,L,D；i＝1,2,L,n；k为当前的迭代次数；表示编号为id的的粒子当前迭代次数为k的速度；表示编号为id的例子当前迭代次数为k的位置；表示当前迭代次数为k时第d个种群的极值；c₁、c₂是非负的常数，称成为加速度因子；r₁和r₂是分布于[0,1]区间的随机数。

步骤3.4：不断更新粒子速度和位置，并且根据新粒子的适应度值更新个体极值和群体极值。同时根据初始化中设定的迭代次数阈值和设定的循环条件进行循环。若迭代次数达到阈值则迭代结束，否则转入步骤3.3，依次循环更新各粒子的速度和位置，最后得到优化后参数值。

以下结合具体的实施例对本发明提出的一种用于轮胎魔术公式的参数辨识及优化方法进行具体说明：

本实施例选用轮胎型号为Hoosier18×6-10R25B，轮胎测试胎压为82.74kPa,垂直载荷为227N,无外倾角，以轮胎纯制动工况下所受纵向力为一实施例，将魔术公式应用于纯制动工况下轮胎所受纵向力与其纵向滑移率和轮胎垂直载荷之间的关系模型。

该工况下的关系模型为：

Y(X)＝Dsin(Carctan(BX₁-E(BX₁-arctan(BX₁))))+S_V

式中：

X₁——纵向力组合自变量：X₁＝(κ+S_h)；

κ——纵向滑移率(车辆制动时为负值)；

C——曲线形状因子，纵向力计算时取B₀值：C＝B₀；

D——峰值因子，表示曲线的最大值：D＝B₁F_Z²+B₂F_Z；

B——刚度因子：B＝BCD/CD；

BCD——纵向力零点处的纵向刚度，

S_h——曲线的水平方向漂移，S_h＝B₉F_z+B₁₀；

S_v——曲线的垂直方向漂移，该工况下S_v＝0；

E——曲线的曲率因子，表示曲线最大值附近的形状，E＝B₆F_z²+B₇F_z+B₈

步骤一：轮胎模型魔术公式中的数据采样。

对轮胎进行一定垂直载荷下的轮胎制动力学特性试验，通过试验中传感器检测并采集得轮胎模型魔术公式中的不同的纵向力Y(x)和纵向滑移率x的数据。

步骤二：根据步骤一中的公式可知需要辨识的参有：{B₀，B₁，B₂，B₃，B₄，B₅，B₆，B₇，B₈，B₉，B₁₀}，然后采用非线性最小二乘方法先初次辨识轮胎魔术公式中的主要参数。主要是通过对步骤一中采样到的数据进行非线性最小二乘拟合，经过数据拟合，初次辨识得到魔术公式的参数值见表1：

表1

步骤三：通过步骤二获得魔术公式初次辨识的参数后，采用基本粒子群算法对魔术公式的参数进行再次辨识以及优化，可得到更精确的结果。

根据需要辨识的魔术公式轮胎模型对粒子种群进行初始化：在一个D维的搜索空间中，由n个粒子组成的种群X＝(X₁,X₂,L,X_n)，其中粒子群内粒子数目n、加速度因子c₁、c₂、惯重权数ω和迭代次数k；根据轮胎模型特点以及工况，取n为11，为避免陷入局部极限极值，可以取ω＝1，c₁＝2.05，c₂＝2.05，k＝50。初始化生成初始种群后，需要辨识的11个参数的值将在解空间运动，粒子通常会跟踪个体极值和群体极值更新个体位置。

因此在这个11维的搜索空间中，由n个粒子组成的种群X＝(X₁,X₂,L,X_n)，其中第i个粒子表示为一个D维的向量X_i＝(X_i1,X_i2,L,X_iD)^T，代表第i个粒子在D维搜索空间中的位置，也代表模型的一个潜在解。根据目标函数即可计算出每个粒子位置X_i对应的适应度值，第i个粒子的速度为V_i＝(V_i1,V_i2,L,V_iD)^T，其个体极值为P_i＝(P_i1,P_i2,L,P_iD)^T，种群的群体极值为P_g＝(P_g1,P_g2,L,P_gD)^T。

步骤四：粒子适应度值计算。首先设置适应度函数为：

Y(X)＝Dsin(Carctan(BX₁-E(BX₁-arctan(BX₁))))+S_V

式中：

X₁——纵向力组合自变量：X₁＝(κ+S_h)；

κ——纵向滑移率(车辆制动时为负值)；

C——曲线形状因子，纵向力计算时取B₀值：C＝B₀；

D——峰值因子，表示曲线的最大值：D＝B₁F_Z²+B₂F_Z；

B——刚度因子：B＝BCD/CD；

BCD——纵向力零点处的纵向刚度，

S_h——曲线的水平方向漂移，S_h＝B₉F_z+B₁₀；

S_v——曲线的垂直方向漂移，该工况下S_v＝0；

E——曲线的曲率因子，表示曲线最大值附近的形状，E＝B₆F_z²+B₇F_z+B₈

进行粒子适应度计算，进行个体极值和群体极值的搜索：

$\sqrt{\frac{1}{N}\underset{i=1}{\overset{n}{\Σ}}\{{\[\left(D_{i}sin\right(C_i\arctan \left(B_i{X}_j-E_i\left(B_i{X}_j-\arctan \left(B_i{X}_j\right)\right)\right))+S_V\]-Y\left(X_j\right)\}}^2}$

本发明提供在参数辨识过程中粒子群适应度值的变化曲线如图2所示。

步骤五：粒子的速度和位置的更新：

速度更新公式

V_id(k+1)＝ω×V_id(k)+c₁r₁×[P_id(k)-X_id(k)]+c₂r₂×[P_gd(k)-X_gd(k)]

位置更新公式：

X_id(k+1)＝X_id(k)+V_id(k+1)

步骤六：不断更新粒子速度和位置，并且根据新粒子的适应度值更新个体极值和群体极值。同时根据初始化中设定的迭代次数阈值和设定的循环条件进行循环。若迭代次数达到阈值则迭代结束，否则转入步骤五，依次循环更新各粒子的速度和位置，更新后的粒子值即为用粒子群优化算法优化后的参数辨识结果，最后得到粒子群算法优化后的辨识参数值见表2。

表2

通过图3以及已知试验中实际测得的数据可以明显对比得优化后的辨识参数值与实际值的误差比优化之前小，说明该方法是可用的，较好的提高了辨识精度。

以上所述仅仅是本发明的一种车辆动力学工况下轮胎的受力实施例而已，也并非对本发明其余工况下的受力分析以及参数辨识的进行了限制，说明本发明采用的用于轮胎魔术公式的参数辨识及优化方法是科学有效的。同时，上述实施例并非用来限定本发明，该方法还可以应用于其他参数较多的非线性模型的参数辨识上，具有一定的普适性和推广价值。