一种基于稀疏点云曲面重构的复杂地质构造建模方法与流程

本发明属于地质技术领域，具体涉及一种复杂地质构造建模方法。

背景技术：

随着油气藏的不断开发，三维地质建模扮演着越来越重要的角色，它作为油气藏勘探开发过程中最基础最重要的研究工作，不仅可以为油气藏开发过程提供重要资料，也可以让地质人员对地下地质构造有更准确的认知，因此，对于三维地质建模技术的研究显得愈发重要。三维地质建模是以钻孔数据、剖面图等原始数据为基础，建立能够准确反映出地下地质构造的数字化模型，作为三维地质建模中最重要的部分，即构造建模，它主要是通过对原始数据进行地震解释得到一系列离散点数据，然后通过插值、曲面重构等处理得到描述地下地质构造的封闭块状模型，即地质构造模型。随着地质勘探技术的不断进步，人们需要对地下地质情况有更清楚、全面的认知，而传统的勘探技术和建模方法不能满足人们更高的要求，因此，对于三维地质构造建模技术的研究是也显得越来越重要。

在三维地质构造建模中，复杂地质构造建模的研究工作是非常有必要的，其复杂性主要体现在：地质体受到一定强度的构造应力作用而发生形变，最后形成了断层或褶皱，二者是复杂地质构造的主要代表。它们破坏了原始的地质结构，其中，断层体现为地质的不连续变形，根据其变形的趋势分为正断层、平移断层、垂直断层和逆断层，而褶皱体现为地质的连续变形。

尽管国内外的众多学者对复杂地质体的三维构造建模方法的研究越来越多，但人们对于复杂地质构造建模的研究主要是以断层为主的构造建模方法研究，即正断层、平移断层、垂直断层和逆断层。现在，对于含断层的复杂地质构造建模的方法也相对比较成熟，而对于含褶皱的复杂地质构造建模方法的研究相对甚少，目前为止，还没有一种相对成熟的方法适用于所有含有褶皱的复杂地质构造建模。

随着地质学和科学技术的进步与发展，三维地质构造建模已经成为数字化与可视化重要的一方面，现在，国内外的大量学者都投入到了复杂地质构造建模的深入研究工作当中。其复杂性主要是由于地质体受到构造应力的作用，使得地质体发生形变，破坏了原始拓扑结构与地质体的连续性，根据形变趋势分为断层与褶皱，二者是复杂地质构造的主要代表。

复杂地质构造建模的基本流程就是：根据地质勘探人员获取的原始点云数据为基础，采用相关的地质曲面重构方法拟合出地质界面，如层位曲面和断层曲面。然后根据地质曲面之间的拓扑关系和约束关系，对地质层面模型进行有规则的裁剪，最后以断层曲面为边界构建出封闭的块状地质模型。

在地质领域的曲面重构方法基本思想就是：对种子点数据进行插值处理，再采用传统的网格剖分方法：即进行连接多边形、剖分三角形等处理，最后完成地质曲面重构。由于地质原始数据的稀疏性，若仅仅采用原始点云数据进行曲面拟合，重构出地质曲面可能会比较凹凸不平、粗糙，为了构造更加光顺的地质曲面，需要利用网格剖分的技术进行曲面重构，而网格剖分需要首先利用空间插值技术。地质领域内常用的空间插值方法主要有反比距离加权法、克里金等。常用的空间曲面网格剖分技术一般分为矩形网格剖分和三角网格剖分，由于通过三角形去描述平面和曲面的形态可以适用于任何复杂的情况下，所以，在地质曲面拟合中会更多的采用三角剖分的方法。

1989年，Mallet等人提出了离散光滑插值方法，并把该方法运用到三维构造建模当中，这是复杂地质构造建模中一个关键技术。1992年，Mallet将该技术运用到几何模型的构建。Lorensen等人在1987年提出了Marching Cubes算法，并且该方法在构造等值面得到了广泛的应用。2002年，袁国栋等人将Marching Cubes算法运用到了Marching Cubes算法曲面重构算法当中。2008年，魏嘉等人结合了Marching Cubes算法和约束Delaunay三角剖分算法并运用于地质曲面的重建，取得了较好的效果。在完成地质曲面重构后，为了构建最后的封闭块状地质模型，需要根据地质曲面之间的约束关系和拓扑关系对曲面进行裁剪处理，Euler等人提供了完整的方法去确定空间曲面的约束关系和拓扑关系。

对于复杂地质构造建模，国内外众多学者研究最多的还是以断层为主的复杂地质构造建模，其中最重要最基础的研究工作就是断面模型的成功构建。2006年，徐能熊等人提出了基于六面体网格剖分的复杂地质构造建模，并取得了较好的效果。2007年，候卫生等人提出线框单元体的方法，为封闭地质块状模型的构建提供了新的思路。2012年，石玉成等人提出了“点-线-面-体”四步法进行断层构造建模。2014年，王威等人通过约束Delaunay三角剖分的方法重构出地质层面和断层面，最后采用一定的规则将其拼接起来形成了封闭块状地质体模型。

对于复杂地质构造的另一种情况，即倒转褶皱，国内外的学者对此的研究相对甚少，2000年，韦宏鹄等人提出了分块建模的方法来进行倒转构造建模，即将地层划分为三个部分，然后对每一个部分采用不用的构造建模方法，最后将这三个部分合成后即可得到多地层褶皱构造的封闭地质体模型。但是该方法的缺点就是最后在合成三个部分的时候，边界会出现问题。

目前为止，对于复杂地质构造的三维建模，国内外的众多学者研究最多的复杂构造往往都是以地质断层为主，即正断层、平移断层、垂直断层和逆断层。而对于倒转这种复杂地质的三维构造建模技术的研究甚少，曾经有学者提出了在倒转地质构造的情况下，采用分块建模的方法，即将地层分为3个部分，使得每个部分都没有多重值的情况，然后对每一部分采用不同的建模方法，最后将3个部分合并后即可得到倒转构造的封闭块状模型。但是由于该方法中最后在合并3个部分的时候，边界会出现问题，所以此方法是有缺陷的。

技术实现要素：

本发明为解决上述技术问题，提出了一种基于稀疏点云曲面重构的复杂地质构造建模方法，在成功构建出层位模型后，根据一定的规则对其侧面进行封闭处理，最后得到封闭的倒转地质构造块状模型，解决了倒转地质三维构造建模的问题。

本发明采用的技术方案是：一种基于稀疏点云曲面重构的复杂地质构造建模方法，包括：

S1、选取投影平面；

S2、在步骤S1选取的投影平面上进行Delaunay三角网连接得到二维的三角网拓扑结构；

S3、通过原始种子点与投影点的一一对应关系恢复出三维空间的三角网，完成三维空间倒转地质曲面重构。

进一步地，所述步骤S1包括以下分步骤：

S11、建立投影平面，用于将原始种子点数据垂直投影到该平面上；

S12、建立最优化模型，将投影点之间的最小距离最大化；

S13、将步骤S12的最优化模型转化为极小化极大值问题；

S14、根据凸函数定义求解步骤S13得到的极小化极大值问题，得到最佳投影平面。

更进一步地，所述步骤S11还包括：所述投影平面满足：

(1)无重值点；任意两个投影点的距离均大于0；

(2)顺序约束关系；依次遍历相邻3个原始种子点对应的3个投影点，第一个投影点与第三个投影点的距离大于第一个投影点与第二个投影点的距离，且第一个投影点与第三个投影点的距离大于第二个投影点与第三个投影点的距离。

更进一步地，所述步骤S12的最优化模型具体为：

目标变量：b

目标函数：min(d(p_i,p_j))→max，i＝1,2,…,n；j＝1,2,…,n；i≠j

约束条件：d(p_i,p_j)>0，i＝1,2,…,n；j＝1,2,…,n；i≠j

d(p_j-1,p_j+1)-d(p_j-1,p_j)>0，j＝2,3,…,n_i-1；i＝1,2,…,m

d(p_j-1,p_j+1)-d(p_j,p_j+1)>0，j＝2,3,…,n_i-1；i＝1,2,…,m

其中，b表示目标变量，d(p_i,p_j)表示第i个投影点和第j个投影点之间的距离，n_i表示每个剖面的种子点数，m表示剖面的个数。

更进一步地，所述步骤S13具体包括以下分步骤：

S131、根据倒转地质构造的种子点数据的特性，单个剖面上的种子点之间的距离相对比较密集，而剖面与剖面之间的种子点之间距离相对比较稀疏，将步骤S12的最优化模型转化为单个剖面上相邻两个种子点对应的投影点之间的距离的最小值问题；

S132、根据约束条件：任意两个投影点的距离均大于0，可知相邻两个投影点之间的距离大于0，将步骤S131的单个剖面上相邻两个种子点对应的投影点之间的距离的最小值问题，转化为单个剖面上相邻两个种子点对应的投影点之间的距离的倒数的最大值最小化问题；

S133、根据任意两个投影点之间的距离与它们的纵坐标之差是成正比，将步骤S132的单个剖面上相邻两个种子点对应的投影点之间的距离的倒数的最大值最小化问题，转化为单个剖面上相邻两个种子点对应的投影点之间的距离的极大值极小化问题。

更进一步地，所述步骤S14具体为：基于纵坐标依次增大，原始种子点对应的投影点各自的纵坐标依次增大，得到投影平面的有效范围，即得到最佳投影平面。

本发明的有益效果：本发明首次提出了对于倒转地质构造的处理方法，考虑倒转地质构造中的地质层位在部分区域存在多重值的情况，不能采用传统的网格方法进行处理；因此提出了投影平面的思想，即将原始种子点数据垂直投影到某个平面上，在平面上进行Delaunay三角网连接，然后通过种子点与投影点的一一对应关系恢复出空间三角网，从而完成复杂地质曲面重构，其中将投影平面的选取转换为最优化数学模型，并再将其转换为凸优化问题及进行快速求解；本发明的方法。

附图说明

图1为本发明实施例倒转地质曲面重构流程图；

图2为本发明实施倒转投影重值点示意图；

图3为本发明实施倒转投影顺序约束关系示意图；

图4为本发明实施多个剖面倒转原始种子点数据示意图；

图5为本发明实施各个剖面的投影点数据示意图；

图6为本发明实施平行投影平面示意图。

具体实施方式

为便于本领域技术人员理解本发明的技术内容，下面结合附图对本发明内容进一步阐释。

如图1所示为本发明的方案流程图，本发明提出一种基于稀疏点云曲面重构的复杂地质构造建模方法，包括：

S1、选取投影平面；并且将原始种子点数据垂直投影到该投影平面上，该投影平面必须满足两个约束条件：

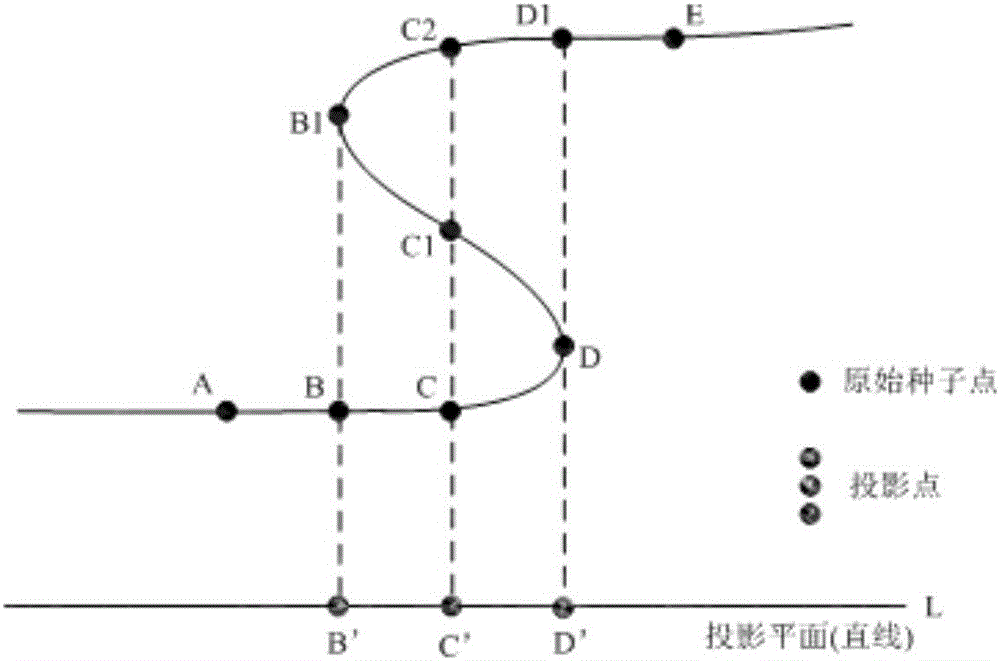
(1)无多重值点，即不能含有两个或两个以上的原始种子点数据垂直投影到投影平面上后，其投影点完全重合，即投影点坐标完全一样。如图2所示，A，B，C，D，C1，B1，C2，D1，E所代表的离散点数据为倒转层位的原始种子点数据，B’，C’，D’所代表的离散点数据为投影点数据，L为投影直线(在二维平面上就是投影平面)。在对原始种子点数据进行垂直投影出来后，B和B1的投影点都是B’，C、C1和C2的投影点都是C’，D和D1的投影点都是D’，这都不符合约束条件(1)，即该投影平面L(即图2中的直线)是无效的。

无多重值点，在数学上可以表达为任意两个投影点的距离都大于0，即，d(p_i,p_j)>0，i＝1,2,…,n；j＝1,2,…,n；i≠j，其中，d(p_i,p_j)表示第i个投影点和第j个投影点之间的距离，n表示投影点的个数。

(2)顺序约束关系。即原始种子点的顺序必须与对应的投影点的顺序必须保持一致。如图3所示，点1,2,3,4,5,6为倒转地质构造的原始种子点数据，点1′,2′,3′,4′,5′,6′为对应的投影点数据，L为投影直线(二维上就是投影平面)，原始种子点的顺序就是1,2,3,4,5,6，而投影点的顺序是1′,2′,5′,4′,3′,6′，显然与原始种子点的顺序不一致，不符合约束条件(2)，因此，该投影平面(直线)是无效的。

顺序约束关系，在数学上可以表达为：对于每个剖面，依次遍历相邻3个原始种子点对应的3个投影点，第一个点与第三个点的距离大于第一个点与第二个点的距离，且第一个点与第三个点的距离大于第二个点与第三个点的距离；即，d(p_j-1,p_j+1)-d(p_j-1,p_j)>0，d(p_j-1,p_j+1)-d(p_j,p_j+1)>0，j＝2,3,…,n_i-1i＝1,2,…,m；p_j-1,p_j,p_j+1为相邻的3个原始种子点对应的3个投影点，n_i表示每个剖面的种子点数，m表示剖面的个数。

在满足约束条件(1)和(2)后，可能会存在多个投影平面，而选择哪一个投影平面比较好是一个难点。如果在投影平面上的离散点数据之间尽量分得开，即投影点之间的距离尽可能的大，这样在投影平面上构建Delaunay三角网拓扑结构的效果比较好，根据原始点与投影点的一一对应关系恢复出空间三角网后，曲面拟合的效果也比较好。而这里投影平面上离散点数据之间尽量分得开，即为投影平面上离散点之间最小距离最大化的那个投影平面是最佳的，最后曲面拟合的效果最优。

如图4所示，该图是多个剖面的倒转原始种子点数据分布图，图中只画出了3个剖面的种子数据，3个平面相互平行，从左往右分别是剖面1的种子点数据，剖面2的种子点数据，剖面3的种子点数据。其中，每个剖面的种子点数据是有顺序关系的，根据原始种子点的顺序A，B，C，D，E，F，G；剖面1中投影点的顺序为A1，B1，C1，D1，E1，F1，G1；剖面2中投影点的顺序为A2，B2，C2，D2，E2，F2，G2；剖面3中投影点的顺序为A3，B3，C3，D3，E3，F3，G3。

由上述描述可知，倒转构造的原始种子点数据所在的剖面相互平行，假设都平行于xoy平面。为了简单处理，假设投影平面垂直于平面，即投影平面的方程为ax+by+c＝0。由于原始种子点数据所在的剖面均平行于xoy平面，所以每个剖面的种子点数据投影到平面后的投影点数据都在同一条直线上。如图5所示，该图为各个剖面的投影点数据示意图，图中画出了3个剖面中种子点数据对应的投影点数据，每一列的圆点为对应剖面的投影点数据，从左往右依次是：剖面1的投影点，剖面2的投影点，剖面3的投影点；可以明显看出每个剖面的种子点数据对应的投影点数据都在同一条直线上。

因此可以只考虑单一剖面上的种子点数据向投影直线的投影情况，且每个剖面都做相似的处理。如果每个剖面的投影数据都满足上述两个约束条件，则所有原始种子点的投影数据都会满足上述两个约束条件。相当于把二维平面的投影问题转化为一维直线上的投影问题，这样就会更便于处理。

如图6所示，该图为单个剖面上的种子点数据与一维投影直线的对应图，L1和L2是两条相互平行的投影直线(单个剖面实际上就是投影直线)，曲线上的点是原始种子点数据，L1和L2上的点是投影点。假设L1满足上述两个约束条件，由于原始种子点是垂直投影到平面上，则L2也一定满足上述两个约束条件，这是因为两条投影直线上的投影点数据之间的相对位置不会改变。为了方便处理，可以假设投影直线经过原点，设投影直线的方程为ax+by＝0，对投影方程做归一化处理后，即为x+by＝0。又由于投影平面垂直于xoy平面，所以可以假设投影平面是π，其方程为x+by＝0。

在对投影方程做归一化处理后，本质上就是排除了y＝0这个平面，即xoz平面，如图6所示，根据倒转构造的种子点数据的分布特征，若选取y＝0这个投影平面，投影点数据一定不会满足上述两个约束条件，这表明直接排除y＝0这个投影平面的情况是可行的。所以，我们假定投影平面π的方程为y＝0是可行的。

在选取投影平面后，将原始种子点数据垂直投影到该选取的投影平面上，为了使得空间曲面拟合的效果尽可能的好，就需要投影平面上的Delaunay三角网连接的效果尽可能的好。如果投影点数据尽可能的分开些，即投影点与投影点之间的距离尽可能的大，也就是说投影点与投影点之间的最小距离最大化，即选出最佳投影平面，那么该投影平面上进行Delaunay三角网连接后的拓扑结构效果最佳，即最后通过一一对应关系恢复出空间三角网后，倒转曲面的三角网拓扑结构的效果最好，最后拟合出的倒转地质曲面效果最佳。

本申请中具体的选取最佳投影平面的计算过程为：

假设原始种子点数据总共有n个，分布在m个剖面，每个剖面的的种子点数目为n_x，其中，x表示剖面的个数，x＝1,2,L,m。为了寻找最佳的投影平面π，本申请建立一个最优化数学模型：

目标变量：b

目标函数：min(d(p_i,p_j))→max i＝1,2,…,n；j＝1,2,…,n；i≠j

约束条件：d(p_i,p_j)>0 i＝1,2,…,n；j＝1,2,…,n；i≠j

d(p_j-1,p_j+1)-d(p_j-1,p_j)>0 j＝2,3,…,n_i-1i＝1,2,…,m

d(p_j-1,p_j+1)-d(p_j,p_j+1)>0 j＝2,3,…,n_i-1i＝1,2,…,m

其中，目标变量b为投影平面方程x+by＝0中的系数，d(p_i,p_j)表示任意第i个投影点和第j个投影点之间的距离。

在上述最优化数学模型中，本申请的目标函数是投影点与投影点之间的最小距离最大化，即：

min(d(p_i,p_j))→max (1)

其中，d(p_i,p_j)表示第i个投影点和第j个投影之间的距离。

由于倒转地质构造的种子点数据的特殊性：单个剖面上的种子点之间的距离相对比较密集，而剖面与剖面之间的距离相对比较稀疏。所以，不用考虑两个剖面的种子点对应的投影点之间的最小距离(因为剖面与剖面之间的距离足够大)，而只考虑单个剖面上种子点对应的投影点之间的最小距离，即单个剖面上相邻两个种子点对应的投影点之间的距离的最小值。则式(1)可以转换为：

min(d(p_i,p_i+1))→max (2)

其中，d(p_i,p_i+1)表示相邻两个投影点之间的距离，由于相邻两个投影点之间的距离是大于0的，所以式(2)可以转换为距离的倒数的最大值最小化，即：

由于两个投影点之间的距离与它们的纵坐标之差是成正比的，所以式(3)可进一步表示为：

其中，y′_i,i+1表示每个剖面相邻两个投影点的纵坐标之差，即：

y′_i,i+1＝y′_i+1-y′_i (5)

由式(4)可以得出，上述最优化数学模型转换为了极大值极小化问题。

根据投影点坐标公式将其带入到式(5)中，得到：

继续化简，得：

其中令：x＝x_i-x_i+1，y＝y_i-y_i+1

则式(7)可以化简为：

将式(8)代入到目标函数中，即式(4)中，得到新的目标函数：

在基于纵坐标依次增大的方法中，有顺序的原始种子点对应的投影点在纵坐标依次增大，即：

y′₁<y′₂<y′₃<…<y′_n-1<y′_n (10)

根据式(10)可以得到投影平面的有效范围，即b的有效范围。

通过将目标函数转化为凸优化问题，可以快速求解，得到最佳投影平面；所述凸优化问题是指目标函数是凸函数，且由约束条件得到的定义域为凸集的最优化问题。下面通过凸函数的定义证明目标函数为凸函数，具体过程为：

由式(10)可以得到，后一个投影点的坐标标比前一个投影点大，即：

y′_i,i+1＝y′_i+1-y′_i>0 (11)

结合式(8)和式(11)可以推出

bx-y>0 (12)

在目标函数只有b一个自变量，所以可以令：

要想证明目标函数为凸函数，可以转换为证明目标函数的二阶导数大于或等于0，即需先证明目标函数中的g(b)的二阶导数大于或等于0，下面，计算g(b)的一阶导数，即：

继续化简，得：

下面，计算g(b)的二阶导数，即：

继续化简，得：

最后化简，得：

再结合式(12)可得：

g”(b)>0 (19)

所以，证明了g(b)是严格凸函数。根据凸函数的定义可知，对于自变量b的定义域中任意两点b₁与b₂和任意实数θ，其中0<θ<1，有：

g(θb₁+(1-θ)b₂)≤θg(b₁)+(1-θ)g(b₂) (20)

对于目标函数，即式(9)，可以转换为：

max{g₁(b),g₂(b),…,g_n(b)}→min (21)

其中g_i(b),i＝1,2,…,n表示相邻两个原始种子点对应的投影点的距离的倒数，且g_i(b)已经证明是关于变量b的凸函数。下面，证明式(21)中的目标函数是凸函数，设目标函数为：

f(b)＝max{g₁(b),g₂(b),…,g_n(b)} (22)

下面根据定义来证明该函数是一个凸函数，对于自变量b的定义域内的任意两点b₁与b₂和任意的实数θ，其中0<θ<1：

再结合式(20)，有：

提取出公因子θ和1-θ，可得：

f(θb₁+(1-θ)b₂)≤θf(b₁)+(1-θ)f(b₂) (27)

所以，根据凸函数的定义，证明了目标函数(22)是凸函数。根据基于纵坐标依次增大的方法，可以得到最后b的有效范围在一个线性区间内，即其定义域是凸集。

本发明提出了一种新的曲面重构方法，即通过投影平面的思想：首先在空间上找到一个新的平面，并且将原始种子点数据垂直投影到该平面上，其中必须满足两个约束条件：(1)无多重值，(2)顺序约束关系。然后在平面上进行Delaunay三角网连接得到二维的三角网拓扑结构，最后通过原始点与投影点的一一对应关系恢复出三维空间的三角网，即完成了三维空间倒转地质曲面重构。包括：

S2、在步骤S1选取的投影平面上进行Delaunay三角网连接得到二维的三角网拓扑结构；

S3、通过原始种子点与投影点的一一对应关系恢复出三维空间的三角网，完成三维空间倒转地质曲面重构。

在平面上进行Delaunay三角网连接得到二维的三角网拓扑结构，最后通过原始点与投影点的一一对应关系恢复出三维空间的三角网，即完成了三维空间倒转地质曲面重构，这部分为现有的常规技术，不是本申请的重点内容，不做详细说明。详细的过程可以参考以下文献：

D.T.Lee,B.J.Schachter.Two algorithms for constructing a Delaunay triangulation[J].International Journal of Computer and Information Sciences,1980,2(9):219-242.

T.K.Dey,J.Giesen.Detecting undersampling in surface reconstruction[M].Discrete and Computational Geometry.Springer Berlin Heidelberg,2003,329-345

徐守乾,朱延娟.稀疏点云的曲面重构[J].中国制造业信息化:学术版,2011,40(2):35-38

魏嘉,唐杰,岳承祺,等.三维地质构造建模技术研究[J].石油物探,2008,47(4):319-327

本领域的普通技术人员将会意识到，这里所述的实施例是为了帮助读者理解本发明的原理，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的权利要求范围之内。