初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法与流程

本发明涉及数据预测技术领域，特别是一种初始序列基于函数变换的灰色预测模型方法。

背景技术：

水运运量规模和增长速度是水运发展的重要指标,它关系到如何科学规划港口、航道、船队、人力资源、船舶和临港工业的布局等。灰色预测由于预测简单，精度高等优点已经广泛的运用到水路运输预测中。

然而经典的gm(1，1)模型存在很多缺陷，根据调查研究，初始序列的光滑度对预测精度的影响较大。本发明对现有的方法进行了改进，将余弦函数与幂函数融入变换函数，提出了初始序列基于函数变换与残差修正相结合的灰色预测模型方法。

技术实现要素：

为解决现有技术的不足，本发明的目的在于提供一种初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，能够有效适应各种数据变化类型，有效的提高模型的预测精度。

为了实现上述目标，本发明采用如下的技术方案：

初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，包括如下步骤：

步骤一，根据预测目标选取预测模型所采用的原始数据序列，此原始数据序

列为一组非负递增数数据序列，记为x⁽⁰⁾，

设原始数据序列为：

x⁽⁰⁾＝{x⁽⁰⁾(1),···,x⁽⁰⁾(n)}，

式中，x⁽⁰⁾(i)＞0i＝1,···,n；

步骤二，对初始序列x⁽⁰⁾进行预处理，将所有数据的范围控制在区间范围内，记为f⁽⁰⁾，预处理的公式如下式所示：

式中，x⁽⁰⁾(k)为初始序列中第k个值，m,m分别为两个控制参数，为了保证初始序列经过变换后满足区间范围内，f⁽⁰⁾(k)为经过预处理后序列中第k个值；

步骤三，对f⁽⁰⁾序列进行函数变换，计算公式如下式所示：

式中，r⁽⁰⁾(k)为经过函数变换得到序列的第k个值；

步骤四，对原始数据序列r⁽⁰⁾做一次累加处理，生成一次累加序列r⁽¹⁾，计算公式如下式所示：

式中，r⁽¹⁾(k)为原始数据r⁽⁰⁾(k)的一次累加序列，累加序列记为：

r⁽¹⁾＝{r⁽¹⁾(1),···,r⁽¹⁾(n)}；

步骤五，一次累加序列r⁽¹⁾满足白色微分方程采用背景值计算公式计算z⁽¹⁾(k)与矩阵b,y，利用最小二乘法求出参数a、u，

z⁽¹⁾(k)通过下式进行计算：

矩阵b、y与参数a、u通过下式进行计算：

(a,u)^t＝(b^tb)^-1b^ty；

步骤六，基于求解出的参数a、u，建立时间响应序列并还原求解出序列的预测值

通过白色微分方程的求解，带入参数a、u可以得到时间响应函数为：

上式离散化得：

式中，r⁽¹⁾(1)＝r⁽⁰⁾(1)，为预测值；

通过下式进行计算：

步骤七，通过还原公式计算预测值的还原值，记为还原公式如下式所示：

步骤八，根据步骤七求解出原始数据序列的预测值后，进行误差检验以判断gm(1，1)模型的预测精度；

步骤九，选出穷举法下最小的相对误差值；首先，通过穷举法并利用计算机编程令取值进行试选，根据取各个值通过组合变换后使用gm(1，1)模型预测得到各个值对应的相对误差，最终选取最小的相对误差，并记录此时对应的取值。

前述的初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，步骤九中，穷举划分精度越小，所得的预测结果越精确。

前述的初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，步骤九中，穷举法对的值进行试选的具体过程为：利用计算机编程令从η开始以步长η增长到1结束。

前述的初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，步骤九中，选取最小的相对误差的具体过程为：取η，进行步骤一到步骤八的实验操作，求出情况下对应的相对误差值，以步长η增长，循环进行步骤一到步骤八操作，当时结束循环，选出每次循环计算出来相对误差值的最小值。

前述的初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，包括如下步骤：

步骤一，根据预测目标选取预测模型所采用的原始数据序列，此原始数据序列为一组非负递增数数据序列，记为x⁽⁰⁾，

设原始数据序列为：

x⁽⁰⁾＝{x⁽⁰⁾(1),···,x⁽⁰⁾(n)}，

式中，x⁽⁰⁾(i)＞0i＝1,···,n；

步骤二，对初始序列x⁽⁰⁾进行预处理，将所有数据的范围控制在区间范围内，记为f⁽⁰⁾，预处理的公式如下式所示：

式中，x⁽⁰⁾(k)为初始序列中第k个值，m,m分别为两个控制参数，为了保证初始序列经过变换后满足区间范围内，f⁽⁰⁾(k)为经过预处理后序列中第k个值；

步骤三，对f⁽⁰⁾序列进行函数变换，计算公式如下式所示：

式中，r⁽⁰⁾(k)为经过函数变换得到序列的第k个值；

步骤四，对原始数据序列r⁽⁰⁾做一次累加处理，生成一次累加序列r⁽¹⁾，计算公式如下式所示：

式中，r⁽¹⁾(k)为原始数据r⁽⁰⁾(k)的一次累加序列，累加序列记为：

r⁽¹⁾＝{r⁽¹⁾(1),···,r⁽¹⁾(n)}；

步骤五，一次累加序列r⁽¹⁾满足白色微分方程采用背景值

计算公式计算z⁽¹⁾(k)与矩阵b,y，利用最小二乘法求出参数a、u，

z⁽¹⁾(k)通过下式进行计算：

矩阵b、y与参数a、u通过下式进行计算：

(a,u)^t＝(b^tb)^-1b^ty；

步骤六，基于求解出的参数a、u，建立时间响应序列并还原求解出序列的预测值

通过求解白色微分方程带入参数a、u可以得到时间响应函数为：

上式离散化得：

式中，r⁽¹⁾(1)＝r⁽⁰⁾(1)，为预测值；

通过下式进行计算：

步骤七，通过还原公式计算预测值的还原值，记为还原公式如下式所示：

步骤八，根据步骤七求解出原始数据序列的预测值后，进行误差检验以判断gm(1，1)模型的预测精度；

步骤九，选出穷举法下最小的相对误差值；首先，通过穷举法并利用计算机编程令取值进行试选，根据取各个值通过组合变换后使用gm(1，1)模型预测得到各个值对应的相对误差，最终选取最小的相对误差，并记录此时对应的取值；

步骤十，对预测结果进行残差修正，首先计算出残差e(k)，(k＝2,···n)；

进一步的对残差序列进行预处理，①若e(k)，(k＝2,···n)都大于零，此时不需要进行处理，直接进行进一步的计算；②若e(k)，(k＝2,···n)都小于零，此时需要对所有的e(k)，(k＝2,···n)都取绝对值；③若e(k)，(k＝2,···n)既有正数又有负数，此时需要加上大于等于|min(e(k))|的数σ，另所有的值都大于等于零；

通过预处理并构成新的序列e＝{e(2),e(3),···,e(n)}，并使用经典的灰色预测，具体计算参造经典的灰色模型；

得到预测值后进行还原，还原方法对应上述三种预处理方法①不需要进行还原；②对预测值都加个负号；③所有预测值减去σ，还原后得到预测序列：计算最终预测值序列y＝{y(1),y(2),···,y(n)}为：

本发明的有益之处在于：本发明提供一种初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，通过对f⁽⁰⁾序列进行函数变换，提高了初始序列的光滑度，使得本发明能够有效适应各种数据变化类型；有效提高模型的预测精度，降低误差；且本方法在最后对预测结果进行残差修正，进一步提高计算精度。

附图说明

图1是本发明gm(1，1)预测模型的运行流程图；

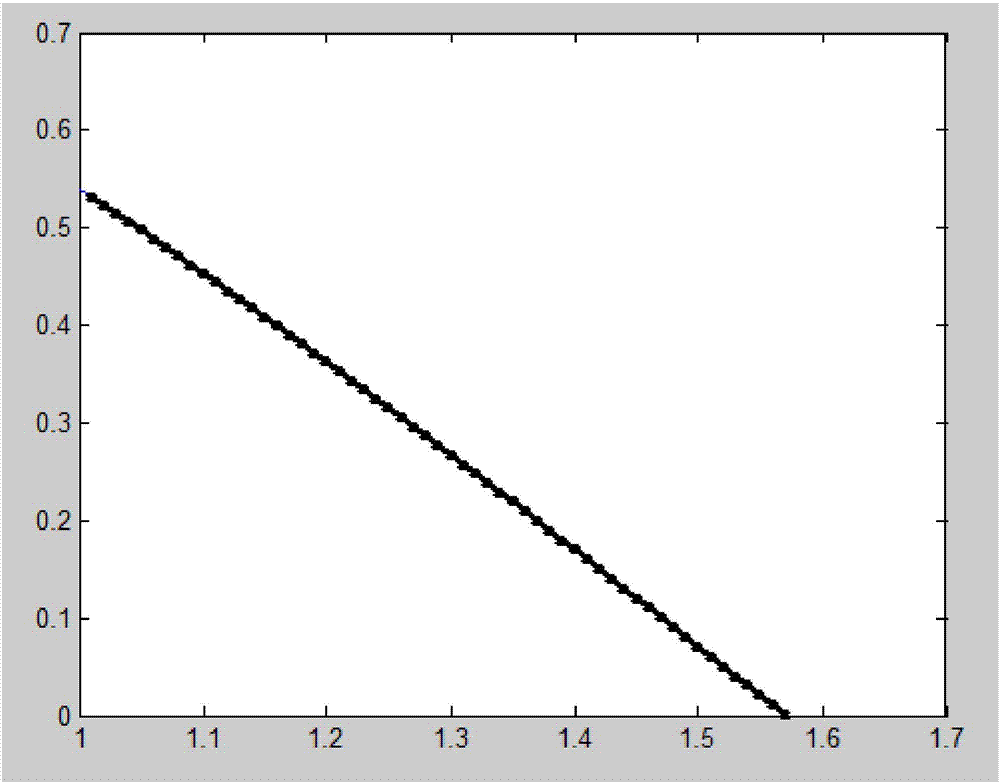
图2是本发明变换函数的图像；

图3是本发明对原始数据序列做一次累加处理的流程图；

图4是本发明穷举法的初始序列变换函数的流程图；

图5是现有技术和本发明的拟合值与实际值的折线比较图。

图6是本发明与现有技术两种方法的拟合值与实际值的折线图。

具体实施方式

以下结合附图和具体实施例对本发明作具体的介绍。

初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，包括如下步骤：

步骤一，根据预测目标选取预测模型所采用的原始数据序列，此原始数据序

列为一组非负递增数数据序列，记为x⁽⁰⁾，

设原始数据序列为：

x⁽⁰⁾＝{x⁽⁰⁾(1),···,x⁽⁰⁾(n)}，

式中，x⁽⁰⁾(i)＞0i＝1,···,n；

步骤二，对初始序列x⁽⁰⁾进行预处理，将所有数据的范围控制在区间范围内，记为f⁽⁰⁾，预处理的公式如下式所示：

式中，x⁽⁰⁾(k)为初始序列中第k个值，m,m分别为两个控制参数，为了保证初始序列经过变换后满足区间范围内，f⁽⁰⁾(k)为经过预处理后序列中第k个值；

步骤三，对f⁽⁰⁾序列进行函数变换，变换函数具体图像如图2所示，计算公式如下式所示：

式中，r⁽⁰⁾(k)为经过函数变换得到序列的第k个值；

步骤四，对原始数据序列r⁽⁰⁾做一次累加处理，生成一次累加序列r⁽¹⁾，具体流程参照图3，计算公式如下式所示：

式中，r⁽¹⁾(k)为原始数据r⁽⁰⁾(k)的一次累加序列，累加序列记为：

r⁽¹⁾＝{r⁽¹⁾(1),···,r⁽¹⁾(n)}；

步骤五，一次累加序列r⁽¹⁾满足白色微分方程采用背景值计算公式计算z⁽¹⁾(k)与矩阵b,y，利用最小二乘法求出参数a、u，z⁽¹⁾(k)通过下式进行计算：

矩阵b、y与参数a、u通过下式进行计算：

(a,u)^t＝(b^tb)^-1b^ty；

步骤六，基于求解出的参数a、u，建立时间响应序列并还原求解出序列的预测值

通过求解白色微分方程带入参数a、u可以得到时间响应函数为：

上式离散化得：

式中，r⁽¹⁾(1)＝r⁽⁰⁾(1)，为预测值；

通过下式进行计算：

步骤七，通过还原公式计算预测值的还原值，记为还原公式如下式所示：

步骤八，根据步骤七求解出原始数据序列的预测值后，进行误差检验以判断gm(1，1)模型的预测精度；

步骤九，选出穷举法下最小的相对误差值；首先，通过穷举法并利用计算机编程令的值进行试选，根据取各个值通过组合变换后使用gm(1，1)模型预测得到各个值对应的相对误差，最终选取最小的相对误差作为本发明的最小相对误差计算值，具体流程参照图4。

需要说明的是：穷举划分精度越小，所得的预测结果越精确。作为一种优选，精度η取值通常为0.1、0.01、0.001、0.0001等。

为了进一步提高计算精度，步骤十，对预测结果进行残差修正，首先计算出残差e(k)，(k＝2,···n)。

进一步的对残差序列进行预处理，①若e(k)，(k＝2,···n)都大于零，此时不需要进行处理，直接进行进一步的计算；②若e(k)，(k＝2,···n)都小于零，此时需要对所有的e(k)，(k＝2,···n)都取绝对值；③若e(k)，(k＝2,···n)既有正数又有负数，此时需要加上大于等于|min(e(k))|的数σ，另所有的值都大于等于零。

通过预处理并构成新的序列e＝{e(2),e(3),···,e(n)}，并使用经典的灰色预测，具体计算参造经典的灰色模型(参见文献1：邓聚龙.灰色系统基本方法[m].武汉:华中理工大学出版社,1987.)；

得到预测值后进行还原，还原方法对应上述三种预处理方法①不需要进行还原；②对预测值都加个负号；③所有预测值减去数σ，还原后得到预测序列：计算最终预测值序列y＝{y(1),y(2),···,y(n)}为：

相对误差的计算，通过下式计算相对误差

穷举法对的值进行试选的具体过程为：利用计算机编程令从η开始以步长η增长到1结束。

选取最小的相对误差的具体过程为：取η，进行步骤一到步骤八的实验操作，求出情况下对应的相对误差值，以步长η增长，循环进行步骤一到步骤八操作，当时结束循环，选出每次循环计算出来相对误差值的最小值，具体流程参照图4。

进一步的η选取的过程为：精度η取值通常为0.1、0.01、0.001、0.0001等，为了确定最佳精度范围，通常可以使用试算法，使用不同的精度进行计算，计算任意一个精度产生的相对误差值，理论上来讲穷举精度选择越密，预测结果也会越精确，但为了减少计算机编程时的计算负荷，本发明将设置一个阈值ω(本发明取0.004％)，当取两个相邻η值得到的最小相对误差值之差小于这个阈值时，此时取前一个η值作为穷举精度，具体流程参照图5。

光滑度提高的理论证明：

为了证明本发明可以提高初始序列的光滑度，本发明从光滑度的定义方面进行证明。

定义1.1设x⁽⁰⁾＝{x⁽⁰⁾(k),k＝1,2,···,n}为非负数据序列，如果则称x⁽⁰⁾为光滑离散序列。

定理1.1x⁽⁰⁾＝{x⁽⁰⁾(k),k＝1,2,···,n}为光滑离散序列的充要条件是是k的递减函数。

定理1.2设有两种数据变换分别为f(x)和g(x),若对任意的非负序列x(k)均有：

则称变换f(x)提高序列的光滑度的效果优于变换g(x)。

证明1：经过函数变换后的序列为光滑离散序列。

初始序列x⁽⁰⁾为非负单调递增函数，通过预处理使其满足区间的单调增函数序列f⁽⁰⁾，已知余弦函数在上为单调递减函数,本发明所使用的变换函数具体图像如图2所示。

已知即：

即函数关于k的单调递减函数，即有：

又因为余弦函数在区间上是大于零的，即有：

因为不等式两边都是大于零的数，将上面两个式子不等式两边进行相乘，不等式符号不变，得到下式：

进行调整后得下式：

根据定理1.1可知经过函数变换后的序列为光滑离散序列。

证明2：经过函数变换后的序列光滑度优于传统的变换方式。

引理2.1若x⁽⁰⁾(k)为递增数列，且x⁽⁰⁾(k)＞e，则

引理2.2若x⁽⁰⁾(k)为递增数列，且x⁽⁰⁾(k)＞1，t≥1，则

引理2.3若x⁽⁰⁾(k)为递增数列，且x⁽⁰⁾(k)＞1，t≥1，则

根据引理可知基于对幂变换的函数光滑度最高，下面将证明本发明提出的函数变换光滑度大于对幂函数的光滑度。

令，

对上式进行求导，得下式：

根据上式可知h'(x)≤0，即证明h(x)为减函数，即有：

不等式两边进行整理后得到下式：

对1,···,k-1分别进行上式计算，不等号方向不变化，所有式子求和后得到如下：

将上式整理后得到下式：

根据定理1.2可知，函数变换能够提升初始序列光滑度。

为了证明本发明能够降低误差，将以长三角2001-2009年水运量序列(单位：万t)作为研究对象，使用本发明与两个现有技术的方法得出的相对误差的来比较分析优劣；

现有技术1：经典的灰色模型(参见文献1：邓聚龙.灰色系统基本方法[m].武汉:华中理工大学出版社,1987.)；

现有技术2：初始序列基于cosx变换的gm(1，1)模型(参见文献2：郑锋,魏勇.提高灰建模数据列光滑度的一种新方法[j].理论新探，2007，18(35)：37-38)；

本发明提出方法的计算步骤：

(1)长三角2001-2009年水运量的原始数据序列为：

x⁽⁰⁾＝{62024,70149,79539,90831,105602,117726,129399,132396,132899}

(2)对初始序列x⁽⁰⁾进行预处理，将所有数据的范围控制在区间范围内，记为f⁽⁰⁾；

(3)对f⁽⁰⁾序列进行函数变换，得到新的数据序列，记为r⁽⁰⁾；

(4)对原始数据序列r⁽⁰⁾做一次累加处理，生成一次累加序列r⁽¹⁾，计算公式与所得序列如下所示：

(5)对一次累加序列r⁽¹⁾采用背景值计算公式计算z⁽¹⁾(k)与矩阵b,y，利用最小二乘法求出参数a、u；

z⁽¹⁾(k)通过下式进行计算：

矩阵b、y与参数a、u通过下式进行计算：

(a,u)^t＝(b^tb)^-1b^ty

(6)基于求解出的参数a、u，建立时间响应序列并还原求解出序列的预测值

通过白色微分方程的求解，带入参数a、u可以得到时间响应函数为：

上式离散化得：

式中，r⁽¹⁾(1)＝r⁽⁰⁾(1)，为预测值。

通过下式进行计算：

(7)通过还原公式计算预测值的还原值，记为还原公式如下式所示：

(8)通过穷举法对的值进行试选，通过步骤9对实施例实验得到η取0.01(当精度取0.1时得到的最小相对误差为2.2864％，当精度为0.01时得到的最小相对误差为2.2817％，相邻相对误差值差大于0.004％，当精度为0.001时得到的最小相对误差为2.2817％，在五位有效数字的情况下相对误差不再变化，即本发明的精度取0.01)利用计算机编程令从0.01开始以步长0.01增长到1结束，根据取不同的值使用组合变换后使用gm(1，1)模型预测得到不同的相对误差，当取0.76时，此时相对误差最小且为2.28％，得到的预测值序列

(9)对预测结果进行残差修正，首先计算出残差e(k)，(k＝2,···n)。

计算结果残差序列e属于第三种情况，即有正数又有负数，此时另序列中所有数都加上6700，得到序列并使用经典灰色模型，得到的预测结果将预测结果减去6700得到预测序列根据下式：

得到的序列相对误差的检验，最终计算得到相对误差为2.14％。

文献1中邓聚龙教授提出的经典的gm(1，1)模型计算：

响应函数的确定：

预测值的还原：

文献2初始序列基于cosx变换的gm(1，1)模型

(1)长三角2001-2009年水运量的原始数据序列为：

x⁽⁰⁾＝{62024,70149,79539,90831,105602,117726,129399,132396,132899}

(2)对初始序列x⁽⁰⁾进行预处理，将所有数据的范围控制在区间范围内，记为f⁽⁰⁾；

(3)对f⁽⁰⁾序列进行cosx函数变换，得到新的数据序列，记为r⁽⁰⁾；

r⁽⁰⁾(k)＝cos(f⁽⁰⁾(k))

r⁽⁰⁾＝{0.5263,0.4704,0.407456709450136,0.3341,0.2420,0.1695,0.1024,0.0855,0.0827}

(4)对原始数据序列r⁽⁰⁾做一次累加处理，生成一次累加序列r⁽¹⁾

r⁽¹⁾＝{0.5263,0.9967,1.4042,1.7383,1.9803,2.1498,2.2522,2.3377,2.4204}

对一次累加序列r⁽¹⁾采用背景值计算公式计算z⁽¹⁾(k)与矩阵b,y，利用最小二乘法求出参数a、u；

z⁽¹⁾(k)通过下式进行计算：

(6)基于求解出的参数a、u，建立时间响应序列并还原求解出序列的预测值

r⁽¹⁾(k+1)＝-2.1706e^-0.2615k+2.6969

通过下式进行计算：

(7)通过还原公式计算预测值的还原值为

通过上述三种计算方法对徐州市2001-2012年省道客车交通量进行拟合计算，计算结果如表1所示。

表1三种计算方法的拟合结果

根据上表所示，本发明提出的改进的gm(1，1)模型平均相对误差为2.14％，经典灰色模型的平均相对误差为4.97％，初始序列基于cosx函数变换的gm(1，1)模型的平均相对误差为3.04％，因此本发明提出的改进的gm(1，1)方法误差较低，精度提升较为明显，拟合结果参照图6所示。根据实验证明，该方法不仅适用于徐州市省道客车交通量的预测，还可以运用到交通其他方面的预测上，具有良好的预测结果。

本发明提供一种初始序列基于余弦函数与幂函数组合变换的灰色预测模型方法，通过对f⁽⁰⁾序列进行函数变换，提高了初始序列的光滑度，使得本发明能够有效适应各种数据变化类型；有效提高模型的预测精度，降低误差；且本方法在最后对预测结果进行残差修正，进一步提高计算精度。

以上显示和描述了本发明的基本原理、主要特征和优点。本行业的技术人员应该了解，上述实施例不以任何形式限制本发明，凡采用等同替换或等效变换的方式所获得的技术方案，均落在本发明的保护范围内。