一种基于对偶边界元和应变能优化分析的弹性断裂仿真方法与流程

本发明属于物理仿真技术领域，具体涉及基于对偶边界元和应变能优化分析的弹性断裂仿真方法。

背景技术

边界元方法作为一种强有力的数值计算工具已经在工程应用的诸多领域得到广泛应用。研究者通过将面向不同应用的基础解带入边界积分方程(boundaryintegralequations,bies)，使得边界元方法具有处理各种应用(特别是在无限场域和开放表面等问题上)。

在断裂仿真方面，对偶边界元方法(dualboundaryelementmethod，dual-bem)在裂口处一侧施加传统位移边界积分方程(displacementbies)的基础上，针对裂口处的另一侧施加独立的受力边界积分方程(tractionbies)来解决重叠裂口表面的问题。dual-bem只对模型的表面进行离散，并针对模型裂口处重叠表面两侧设定不同的边界积分方程来解决系统退化问题，在线性弹性断裂仿真应用中具有非常明显的优势，但是也必须要面对求解各种奇异边界积分的情况。

对模型断裂过程的建模包含几何方法和物理方法。刚体断裂的模拟可以通过预定义的方法或者动态计算应力来计算如何断裂。在模型上预定义的方法可以事先设计出一个断裂模式，这个模式可以是从某一断裂点开始，或者裂纹没有集中到某一断裂点，在断裂时会用预定义的断裂模型来代替，这样速度快但缺少真实性。而从物体的内应力动态计算断裂的方法，可以产生很真实的从某一点开始的很真实的断裂模式，但需要很大的计算量，在实时应用中不太适用。脆性断裂通常指硬体之间在裂纹张开和扩展时，只有很小的弹性变形。

三维断裂仿真的主要挑战在于裂纹延展过程中的几何方面的更新。一般地，断裂过程中的裂纹增长幅度一般会小于网格分辨率两个数量级，此外，考虑到裂口延展的自由性，对几何网格的更新带来了巨大的困难。更重要的是，网格更新所带来的复杂性会导致在仿真过程中频繁出现不连续性和奇异性，这对断裂仿真的数值求解方法提出了新的要求。如果采用体网格细分方法来表示裂口，受网格最小颗粒度和数值连续性的限制，不可能准确地符合实际的裂口，而这种病态的网格反映到物理系统中会导致系统的退化。有限元方法作为一种在较为常用的断裂建模方法，对此类问题的支持是十分无力的。对于裂口处的细分网格操作所导致的大规模网格，有限元方法的效率会出现大幅度的下降，低质量的网格甚至会影响有限元方法的收敛率。不仅如此，传统有限元方法的形函数是不能表示奇异性结果的，如何表示奇异的应力是有限元方法面临的一大挑战。

技术实现要素：

为解决现有技术存在的问题，本发明提出一种基于对偶边界元和应变能优化分析的弹性断裂仿真方法，该方法主要利用对偶边界元方法来表示含有重叠裂口表面的模型，并采用半解析方法来求解超奇异边界积分方程。在断裂的物理仿真过程中，通过引入接触力模型来表示来自接触载荷和裂纹前端应变能释放的连续属性，并且在断裂持续时间段内对裂纹的延展距离计算断裂因子来对裂口端的延展进行精确控制。

本发明是采用以下的技术方案实现的：一种基于对偶边界元和应变能优化分析的弹性断裂仿真方法，包括如下步骤：

步骤(1)、将目标模型及其裂纹进行对偶边界积分方程建模；

步骤(2)、基于分段光滑表面的边界积分方程离散；

步骤(3)、对边界积分方程中奇异的被积函数采用奇异性消减技术进行统一处理；

步骤(4)、边界积分方程中自由项的求解；

步骤(5)、在仿真过程中，使用连续接触模型对断裂产生过程进行准确建模；

采用弹性球体接触的hertz模型建立连续接触时间段，在接触时间段内，通过定义随时间变化的外力来表示接触过程中受力的变化，通过用户指定的仿真时间步以及得到的连续接触时间段，将断裂置于一个连续的接触时间段内，来表示外力作用在模型表面的动态过程；

步骤(6)、在仿真过程中，使用应力强度因子来描述裂纹附近的应力场；

在模型受连续外力作用下进行形变仿真，得到裂口表面边界元素的位移，从而得到裂口的张开位移，在裂纹的前沿处对延展点建立局部坐标系，将张开位移投影到局部坐标基向量上，并计算应力强度因子，当延展点被多个裂纹共享时，通过对多个裂纹中的应力强度因子求平均值得到最终的应力强度因子；

步骤(7)、在产生断裂的过程中，根据表面应力分析进行断裂的初始化，并且在裂纹上基于应力强度因子进行延展；

针对边界元素的表面应力分析，首先获得当前元素的形变梯度，并得到三角面片的firstpiola-kirchhoff应力张量，当最大应力超过了材料强度，在当前三角面片上生成新的裂口；对裂纹上的点计算其应力强度因子，当有效应力强度大于材料的断裂韧性时进行裂纹的延展，在裂纹的延展过程中，计算延展的速度和延展的角度。

进一步地，步骤(1)包括：采用betfi-somigliana等式来对目标模型的区域ω建立边界积分方程；源点处的边界积分方程通过源点和域边界的场点之间的距离所构成的kelvin基础解来表示；将域中的裂纹建模成一个张开型表面，使用对偶边界元将三组表面建模成独立的位移边界积分方程，并将重叠表面上的位移边界积分方法对源点求导，得到受力边界积分方程。

进一步地，步骤(2)包括：对在计算机图形学领域内广泛存在的分段光滑表面模型进行线性离散；边界积分方程在三角面片集合上的求解采用正常的数值积分方法；对于具有数值奇异性面片集合的边界积分方程求解，需在源点处建立剔除域。

进一步地，步骤(3)包括：采用奇异性消减技术对边界积分方程中奇异的被积函数进行统一的处理；将极坐标系下的奇异的被积函数进行taylor展开，使得被积函数的奇异项显式地表达，通过把这些奇异项从被积函数减去，得到一个不含奇异项的正规的被积函数；对被移除的奇异项求得它们的解析解，并将结果带回到边界积分方程。

进一步地，步骤(4)包括：采用球形剔除域，对于源点周围的边界元素所在的切平面集合与球形剔除域进行相交操作，得到位于球面上的顶点集合和轮廓弧线集合；定义如下变量集合：切平面集合，切平面集合的外法线集合，两两相交切平面的夹角弧度集合；得到源点所在局部表面的集合结构相关的系数矩阵。

与现有技术相比，本发明的优点和积极效果在于：

1、提出了一种采用对偶边界元方法的仿真断裂，该方法对重叠断裂表面的两侧分别使用位移边界积分方程和受力边界积分方程来表示，对两个重叠表面的采样点进行独立地建模。并对随之产生的各种奇异积分方程，采用半解析方法和鲁棒的积分变换方法来剔除奇异积分方程对数值求解的影响。

2、引入连续的接触力模型，能够将断裂仿真中施加优势负载的过程显式地表示成一个连续变化的时间区间，并能获得连续变化的负载，对断裂生成过程进行时间序上的连续控制，扩展断裂的应用场合。

3、提出了一种针对断裂延展过程中对断裂前端延伸和应变能量的显著性特征分析方法。一方面简化了裂纹生成过程中参数的计算，提高计算效能，另一方面，使得裂纹生成能够体现对其先验数据的影响。

附图说明

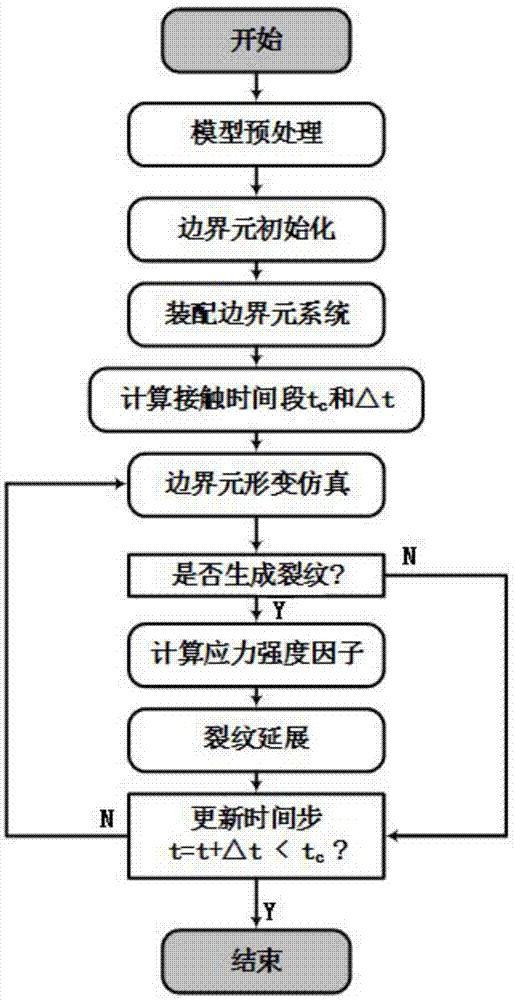
图1为断裂仿真流程图；

图2为边界元积分方程域示意图；

图3为分段光滑表面网格模型示意图；

图4为非光滑表面局部坐标投影示意图；

图5为裂纹延展的局部坐标系；

图6为裂口负载模式；

图7为全局坐标系、局部坐标系、保角坐标系变换示意图；

图8为计算由五个切平面构成的自由项的几何结构示意图；

图9为人类股骨(髀骨)断裂仿真结果图；

图10为人体第五腰椎拥有不同断裂韧性断裂仿真结果图。

具体实施方式

本发明提出一种基于对偶边界元和应变能优化分析的弹性断裂仿真方法，下面结合具体方法步骤，介绍本发明原理。

1)分段光滑表面的对偶边界元方法建模

步骤(1)、采用betfi-somigliana等式来对目标模型的区域ω建立边界积分方程。源点处的边界积分方程通过源点和域边界的场点之间的距离所构成的kelvin基础解uij和tij来表示，其中kelvin基础解表示了在源点处施加了一个单位负载(unitload)后，经过材质影响后，反应到场点处的位移。当场点趋近源点时，基础解uij具有弱奇异性(weaksingularity),此类弱奇异项可以通过极坐标变换(polarcoordinatetransformation,pct)的方法将uij转换成可积的被积函数(integrableintegrand)。tij具有强奇异性(strongsingularity),因此需要引入柯西主值积分(cauchyprincipalvalue，cpv)，来进行处理。当目标模型的域ω中含有裂纹时，将域中的裂纹建模成一个张开型表面，域ω边界γ变成了三部分(γ＝γr+γc++γc-)其中γc+,γc-是重叠的表面，它们的位置相同，方向相反，在这里我们假设在γc+,γc-上没有受力(traction-free)。使用对偶边界元(dual-bem)将三组表面建模成独立的位移边界积分方程(dbies)，并将重叠表面上的位移边界积分方法对源点求导，得到受力边界积分方程(tbies)。

步骤(2)、本发明所用到的边界元方法主要针对的是计算机图形学领域，需要对在计算机图形学领域内广泛存在的分段光滑表面模型进行线性离散(lineardiscretization)。由于使用分段光滑表面作为模型的边界，导致了源点s是一个不连续(non-smooth)的点，被多个三角面片共享(如图3(a))。由于在边界积分方程中的被积函数f对场点x(积分点)到源点s的距离具有奇异性，将分段连续表面γ分成了两个部分：奇异面片集合γs和三角面片集合γr，其中奇异面片集合γs是由共享源点s的面片组成的(如图3(a)中的绿色部分)，余下的灰色部分构成了三角面片集合γr。边界积分方程在三角面片集合上的求解采用正常的数值积分方法，并能获得良好的计算精度。对于奇异面片集合的边界积分方程求解，方法需要在源点s处建立剔除域(excludeddomain)，该区域是一个以源点s为圆心的半径为ε的球体(如图3(b))，方法采用球型剔除域是为了利用它在对自由项cij计算时的优点。分段光滑表面的对偶边界元方法建模往往同样条函数(nurbs)一起使用，样条函数对于模型网格的表示要求较高，虚拟手术模型网格数据(或者说图形学领域广泛使用的网格模型)中，一般使用分段光滑网格(三角网格)，本发明在边界元方法与图形学离散方法之间建立了链接，使得边界元方法可以应用在图形学领域，这种链接不是简单的尝试，而是提出了在三角网格上有效使用边界元方法需要进行的数值优化方法，否则会导致运算不收敛的情况。

步骤(3)、经过步骤(2)的处理得到了一个在分段光滑表面上定义的边界积分方程。方程中含有各种奇异的被积函数。为了能够对这些奇异的被积函数进行统一的处理，采用奇异性消减技术(singularitysubtractiontechnique，sst)。将极坐标系下的奇异的被积函数进行taylor展开，使得被积函数的奇异项可以显式地(explicitly)表达，通过把这些奇异项从被积函数减去，得到一个不含奇异项的正规的(regular)被积函数。对被移除的奇异项求得它们的解析解(analyticsolution)，并将结果带回到边界积分方程。通过使用奇异性消减方法可以避免公式边界积分方程中的极限操作。

2)边界元方程的数值求解

步骤(4)、在边界元建模过程中，somigliana恒等式一般包含了两部分，一部分是通过边界积分方程对具有奇异属性的kelvin基础解进行求解，另一部分是与源点所在局部表面的几何结构相关的系数矩阵c。对于本发明所涉及的在分段光滑表面上建模三维弹性断裂问题，采用显式计算技术，该技术支持在分段光滑表面上显式地计算被任意多个切平面所共享的边界顶点处的系数矩阵c。本步骤采用了专为多边形网格开发的自由项计算技术，相比于传统的应用场景，如cad设计，该领域的集合模型是基本固定的，都是由各种基本几何形状进行拼接，所以，它们计算自由项的方法是，事先(穷举)计算好(使用积分等运算量大的方法)，使用的时候，去引用(查表)，本发明采用的方法能够对于任意多边形几何结构继续快速计算，很好地适用于断裂过程中出现的复杂的几何情况。

3)基于连续接触模型的断裂仿真方法

步骤(5)、为了更好地对断裂的产生过程进行准确地建模，引入连续接触模型。采用弹性球体接触的hertz模型来建立连续接触时间段。通过定义随时间变化的外力来表示接触过程中受力的变化，由于hertz接触模型是一种非粘着接触模型(non-adhesivecontactmodel)，将接触外力视为一个正弦函数(sinusoidalfunction)。通过用户指定的仿真时间步以及得到的连续接触时间段，将断裂置于一个连续的接触时间段内，来表示外力作用在模型表面的动态过程。

步骤(6)、对于裂纹的扩展，因为应力在裂纹尖端具有奇异性，所以使用应力强度因子(stressintensityfactors,sifs)来描述裂纹附近的应力场。在模型受连续外力作用下进行形变仿真，得到裂口表面边界元素的位移，从而得到裂口的张开位移(crackopeningdisplacement,cod)。计算应力强度因子需要在在裂纹的前沿处对延展点建立局部坐标系，对于延展点c，根据其所在裂纹及裂纹所属边界元素的法线以及平行于裂纹的切线，建立相互垂直的局部基向量，将张开位移投影到局部坐标基向量上，并计算应力强度因子；当延展点被多个裂纹共享时，通过对多个裂纹中的应力强度因子求平均值得到最终的应力强度因子。

步骤(7)、对于物体断裂过程的建模需要处理裂纹的初始生成(crackinitiation)和延展(crackpropagation)。断裂的生成是基于表面应力的分析，对模型拥有的所有边界元素逐一计算其主应力和主应力方向，首先获得当前元素的形变梯度(deformationgradient)，并得到三角面片的firstpiola-kirchhoff应力张量，当最大应力超过了材料强度，在当前三角面片的质心，以最大应力的方向为裂口表面的法线，插入新的裂口。对裂纹上的点计算其应力强度因子，当有效应力强度大于材料的断裂韧性时进行裂纹的延展，在裂纹的延展过程中，计算延展的速度和延展的角度。

下面结合附图和具体实施方式对本发明做进一步详细地说明。

图1给出了基于对偶边界元和应变能优化分析的弹性断裂仿真过程的总体处理流程，本发明实施例一种基于对偶边界元和应变能优化分析的弹性断裂仿真方法，其步骤包括：

步骤(1)对于三维的线性弹性问题，本方法采用betfi-somigliana等式来对目标模型的区域ω(如图2所示)建立边界积分方程(见公式1)。

在公式1中，源点(sourcepoint)s处的边界积分方程可以通过s和域ω边界的场点(fieldpoint)x之间的距离r(r＝|s-x|)所构成的kelvin基础解uij和来表示。其中，kelvin基础解uij表示了在源点s处施加了一个单位负载(unitload)后，经过材质影响后，反应到场点x处的位移。在本方法中，当场点x趋近源点s时(r→0)，公式1中的uij具有弱奇异性(weaksingularity),uij＝o(r^-1),此类弱奇异项可以通过极坐标变换(polarcoordinatetransformation,pct)的方法将转换成可积的被积函数(integrableintegrand)。不幸的是，当r→0时，tij具有强奇异性(strongsingularity),tij＝o(r^-2),因此需要引入柯西主值积分(cauchyprincipalvalue，cpv，用符号表示)，来进行处理。公式1中的u和t分别表示场点处的位移和受力，下标i,j表示三维空间中的方向(i,j＝1,2,3)。

当目标模型的域ω中含有裂纹时(如图2(b)所示)，本方法将裂纹建模成为一个张开型表面(opensurface)。对于图2(b)中的情况，域ω边界γ变成了三部分(γ＝γr+γc++γc-)其中γc+,γc-是重叠的表面，它们的位置相同，方向相反，在这里我们假设在γc+,γc-上没有受力(traction-free)。对偶边界元(dual-bem)通过将三组表面建模成独立的位移边界积分方程(dbies)，并将重叠表面γc-上的位移边界积分方法对源点s求导，得到受力边界积分方程(tbies)来解决了这个问题(如公式2，公式3所示)。可以看到，受力边界积分方程中的被积函数和由于求导操作使得它们在源点s处具有了强奇异性,vij＝o(r^-2)和超奇异性(hypersingularity)，wij＝o(r^-3)，分别用柯西主值积分符号和hadamard有限部分(hadamardfinitepart，hfp)积分符号来表示。

公式2中γc+的下标“+”和公式3中γc-的下标“-”是为了区别来自裂口处两侧的重叠表面。公式2和公式3中左侧出现的被称为自由项(freeterms)，该项是由somigliana等式的推导产生的，cij反应了源点s处的几何结构。

步骤(2)由于所用到的边界元方法主要针对的是计算机图形学领域，需要对在计算机图形学领域内广泛存在的分段光滑表面模型(如图3(a)所示)进行线性离散(lineardiscretization)。假定所使用的模型是由c¹连续的三角面片(patches)组成的分段光滑表面，并对其进行线性断裂分析。由于使用分段光滑表面作为模型的边界，导致了源点s是一个不连续(non-smooth)的点，被多个三角面片共享(如图3(a)所示)。不仅如此，由于在边界积分方程中的被积函数f(在这里，f可以是u,t,w,v中的任何一个)对场点x(积分点)到源点s的距离具有奇异性，很自然地将分段连续表面γ分成了两个部分：奇异面片集合γs和三角面片集合γr，其中奇异面片集合γs是由共享源点s的面片组成的(如图3(a)中的绿色部分)，余下的灰色部分构成了三角面片集合γr。边界积分方程在三角面片集合上进行求解时可以采用正常的数值积分方法(如gaussquadraturerule)，并能获得良好的计算精度。对于奇异面片集合的边界积分方程求解，方法需要在源点处建立剔除域(excludeddomain)，该区域是一个以源点s为圆心的半径为ε的球体(如图3(b)所示)，极坐标下的形式是ρ＝ε。采用球型剔除域是为了利用它在对自由项cij计算时的优点。经过上面的处理，在奇异面片集合γs上公式1变成了公式4的形式。

公式4是somigliana等式的理论形式(theoreticalform)，为了将公式4转换成在数值计算上可用的形式需要进行两处修改。第一是将每一个满足c¹连续的任意三角面片从全局空间映射(mapping)到内蕴几何空间(intrinsicgeometricspace)中的规范域(本发明使用直角三角形)，以便对其进行数值积分。为了处理奇异性被积函数，我们采用极坐标(polarcoordinates)来表示参量空间。在图4中显示了位于非光滑边界处的顶点被多个面片共享的源点s和s的剔除域tε在坐标变换中的状态。在图4(b)中，可以看到在极坐标系下，是以源点s在内蕴几何空间中的映像(image)为原点的。需要注意的是，源点s处的球型剔除域(sphericalexcludeddomain)经过坐标变换之后并不一定在内蕴几何空间中保持球型(如图4(b)所示)。经过极坐标坐标变换，公式4的被积函数uij(s,x)uj(x)和tij(s,x)tj(x)变成了和其中n代表场点x在内蕴几何空间中的关于源点s的形函数，j表示从全局空间到内蕴几何空间的雅克比变换(jacobiantransformation)，ρ代表极半径(polarradius),θ代表极角(polarangle)。第二是将公式4变成在多个面片共享源点s情况下的边界积分方程(见公式5)，在转变的过程中要保持映射形式在相邻面片之间的连续性。在公式5，n表示的是共享面片的数量。

步骤(3)经过了步骤(2)的处理，得到了一个在分段光滑表面上定义的边界积分方程，公式5，方程中含有各种奇异的被积函数。为了能够对这些奇异的被积函数进行统一的处理，我们采用奇异性消减技术(singularitysubtractiontechnique，sst)。奇异性消减方法首先将极坐标系下的奇异的被积函数进行taylor展开，使得被积函数的奇异项可以显式地(explicitly)表达，通过把这些奇异项从被积函数减去，得到一个不含奇异项的正规的(regular)被积函数。最后对被移除的奇异项求得它们的解析解(analyticsolution)，并将结果带回到边界积分方程。通过使用奇异性消减方法可以避免公式5中的极限操作。为了方便描述，本方法只对超奇异(hyper-singular)被积函数进行奇异性消减操作，见公式6。为了使用奇异性消减方法，本方法假定位移向量(displacementvector)u在场点x趋近于源点s时满足连续条件，记做u∈c^0,α(s)。在位移向量u满足连续条件的基础上，方法能够对公式6中的奇异性积分项进行级数展开操作，从而得到公式7。

在公式(5-7)中和是两个只与极角(polarangle)θ相关的函数。执行奇异性消减操作的过程可以表示成公式8，公式8中右侧的双重积分(doubleintegral)方程已经消减了(subtraction)奇异项其外侧的极限操作与积分方程实现了解耦，可以被当做正常积分方程进行数值积分处理。

公式8右侧的单层积分(singleintegral)是需要被进行解析求解的奇异项部分。最终步骤(2)得到的公式5可以被处理成只含有常规积分方程的形式，见公式9。对于强奇异项(strongsingularterm)，弱奇异项(weaksingularterm)而言，它们的处理方式和超奇异项是相同的，而且处理上会更简单一些。

步骤(4)针对本方法所面临的分段光滑表面上三维弹性断裂边界元建模问题的求解提供稳定高效的数值求解方法。从数值积分和自由项求解两方面对现有方法提供进一步的数值优化。经过步骤(3)的处理，初始的含有超奇异性被积函数的边界积分方程，公式1，已经通过奇异性消减方法(sst)转变成为规则的数值积分方程，见公式9。在公式9中，可以看到在对含有奇异性被积函数的边界积分方程进行奇异性消减处理中，使用了极坐标来对参照空间进行表示(见步骤(2))以利用极坐标在处理奇异性被积函数方面的优势。但是也需要注意到，虽然极坐标表示的规则的数值积分方法同样可以采用标准的高斯数值积分方法(standardgaussianquadraturerules)来对其进行求解，但是需要通过加大对积分点的采样密度来满足数值计算精度。不仅如此，对于边界元素(本发明使用三角面片，triangleelement)具有较大纵横比(aspectratio)的情况，元素所对应的被积函数仍然会具有奇异属性。出现这种情况的原因在于通过公式7所得的对被积函数的laurent级数展开形式中，函数虽然已经与极轴变量ρ进行了解耦，但是由于其仍然是极角θ的函数，在对极角θ进行积分操作过程中仍然会显现出来自极角θ奇异性。针对上述问题，通过将公式7得到的极角θ的函数投影变换到稳定的保角空间中，来提高现有边界积分方程的数值求解稳定性。

对于具有较大纵横比的边界元素来说，公式7中所得的函数具有如下表达形式：

其中分子处的vi(θ)是θ的函数，p是由下标i确定的常数。函数a(θ)是一个反映了边界元素几何形状信息的函数，其展开式如公式11所示，可以看到公式11中的表示了边界元素的全局坐标到局部坐标(ξ1,ξ2)上映射的基向量。我们通过定义两个空间基向量长度之比λ和两个空间基向量的夹角γ的余弦cos(γ)来对投影空间进行度量，详见公式13。由公式13可以得到两个辅助系数和μ，见公式14。对公式11使用倍角公式并将公式13带入，可以得到新的函数a(θ)的表达式，公式12。可以看到，当μ趋近于1时，系数θ可以通过使导致函数a(θ)→0，进而导致函数拥有奇异属性。从几何的角度看，有两个因素导致了上述情况(μ→1)的出现：(1)由于投影空间基向量u1和u2之间趋近于重叠(夹角γ→0)或者平行(夹角γ→π)导致；(2)由于|u1|和|u2|的比值趋于0或者无穷，即纵横比过大，导致(λ+λ^-1)²→∞。

解决此类问题的方法就是在现有全局坐标系(图7)向局部坐标系(图7b)投影的基础上再进行一次保角变换(conformaltransformation)，如图7c所示，通过保角变换使得新的投影空间基向量满足如下条件：

当将新的基向量带入到公式12中，函数a(θ)由之前的关于极角θ的函数变成了一个常数项由此带来的好处在于：(1)由于a(θ)是一个常数项，公式10中的对于极角θ的奇异性已经被解耦了；(2)一个简单的公式10可以降低沿着极角θ进行数值积分的复杂度。

为了实现这一目标，需要计算两个辅助系数和(见公式16)，用来表示新的投影空间中点的坐标，如图7(c)所示，其中λ和cos(γ)由公式(5-23)定义。于是可以得到新的投影矩阵t(见公式17)，对现有的局部坐标系(见图7b)使用投影矩阵t进行投影，得到了新的局部坐标(见图7c)，可以看出，新的保角空间的基向量和满足公式15。由于进行了新的保角空间投影，所以需要对公式9进行修改，得到公式18。公式中的|t^-1|由公式17所定义，极角θ变成了新的投影空间中的极角。

对于本方法所涉及的在分段光滑表面上建模三维断裂问题，采用自由项显式计算技术，支持在分段光滑表面上显式地计算被任意多个切平面所共享的边界顶点处的自由项系数矩阵。

为了描述方便，下面通过一个示例来说明对系数矩阵c的计算过程，该过程可以被运用到分段光滑表面的通用情况中，包括重叠断裂面的情况。如图8所示，在示例中假设当前源点s被五个边界元素(满足c¹连续条件的任意三角面片)所共享。由于采用了球型剔除域(见步骤(2))，所以5个边界元素所在的切平面集合π与球型剔除域进行相交操作，得到了位于球面上的顶点集合为v＝{v1,v2,v3,v4,v5}和轮廓弧线集合为γ＝{γ1,2,γ2,3,γ3,4,γ4,5,γ5,1}。在这里，将顶点和轮廓弧线进行顺时针排序，如图8所示。为了方面描述，定义如下变量集合：(1)定义切平面集合π＝{π1,2,π2,3,π3,4,π4,5,π5,1}；(2)定义平面集合π的外法线集合为n＝{n1,2,n2,3,n3,4,n4,5,n5,1}；(3)定义两两相交切平面的夹角弧度集合为α＝{α1,α2,α3,α4,α5}，对于αi的计算参见公式19：

αi＝π+sgn((ni-1,i×ni,i+1)·ri)arccos(ni-1,i·ni,i+1)(19)

在公式19中，ri＝r(vi)＝vi-s，s表示源点。sgn(x)是符号函数。

至此，我们可以得到一个由n个切平面相交所构成的局部几何结构所对应的系数矩阵c的通用公式20。使用公式20得到的是一个针对源点s的3×3矩阵c＝{cij}，其中i,j＝1,2,3。

步骤(5)为了更好地对断裂的产生过程进行准确地建模，本方法引入连续接触模型，将断裂置于一个连续的接触时间段内，来表示外力作用在模型表面的动态过程。在接触时间段内，通过定义随时间变化的外力来表示接触过程中受力的变化。为了建立连续接触时间段，本发明采用弹性球体接触的hertz模型，见公式21。

其中，m代表质量，e代表弹性模量，r代表接触球的半径，v代表模型与外界接触时的速度，c是hertz模型的常系数(本发明所使用的参数，c＝2.87)。通过用户指定的仿真时间步δt以及公式21得到的连续接触时间段可以将断裂过程视为一个时间段内的仿真操作。

由于hertz接触模型是一种非粘着接触模型(non-adhesivecontactmodel)，本方法将接触外力视为一个正弦函数(sinusoidalfunction)，见公式22。

其中，fmax代表接触过程中模型表面所受到的最大外力。

步骤(6)针对裂纹的扩展，因为应力在裂纹尖端具有奇异性，所以使用应力强度因子(stressintensityfactors,sifs)来描述裂纹附近的应力场。在模型受连续外力作用下进行形变仿真，得到裂口表面边界元素的位移，从而得到裂口的张开位移(crackopeningdisplacement,cod)，并在裂纹处根据张开位移计算应力强度因子(sif)。由此可见，裂纹延展是以裂纹尖端为基础，根据应力强度因子和模型的材料属性进行扩展的过程。

计算应力强度因子需要在裂纹的前沿处对延展点建立局部坐标系。对于延展点c所处的局部坐标系来说，首先要确定延展点c所在的裂纹ct以及裂纹所属的边界元素eltct，得到边界元素eltct的法线n1以及平行于裂纹ct的切线n3，通过n1与n3的向量积(crossproduct)得到垂直于裂纹ct的法线n2，如图5所示。在图5中，n1，n2，n3是三个相互垂直的局部基向量，其中n1垂直于边界元素eltct，对应于张开方向的受力(见图6中modei)，n2垂直于裂纹ct，对应于剪切方向的受力(见图6中modeii)，n3平行于裂纹ct，对应于滑动方向的力(见图6中modeiii)。

对于δu可以通过边界元素eltct中不属于裂纹ct的顶点p来得到。得到张开位移δu之后需要将其投影到局部坐标基向量上，得到δui，δuii和δuiii，然后根据公式13计算应力强度因子ki，kii和kiii，公式23中的μ代表剪切模量(shearmodulus)，μ＝e/(2+2v)，e代表杨氏模量，v代表泊松比，r代表顶点p到裂纹ct的距离。当延展点被多个裂纹共享时，可以通过对多个裂纹中的应力强度因子求平均值得到最终的应力强度因子。

步骤(7)对于物体断裂过程的建模需要处理裂纹的初始生成(crackinitiation)和延展(crackpropagation)。对于边界元方法来说，断裂的生成是基于表面应力的分析，计算边界元素(三角面片)的最大主应力(maximalprincipalstress)，当最大主应力超过材料强度时就会导致断裂现象。对模型拥有的所有边界元素逐一计算其主应力和主应力方向，然后检查当前边界元素是否需要产生裂纹，当满足产生裂纹条件时，以当前主应力方向作为裂口表面的法线初始化裂口，并以这些裂纹为基础可以进行裂纹的延展。当没有新的裂纹面产生时裂纹生成结束。

在裂纹初始化阶段，为了执行边界元素的表面应力分析，首先要获得当前元素的形变梯度(deformationgradient)，考虑到本发明所采用的的边界元素为空间三角形，它的三个顶点在形变之前和形变之后的状态不能完全确定空间三角形的仿射变换(这是因为缺少了垂直于空间三角形的维度)。为了解决这个问题，本发明通过为空间三角形增加其垂直方向的点，见公式24。假设空间三角形的三个变形前的顶点为vi,i＝1,2,3，三个变形后的顶点为公式24中的v4就是新增的垂直于空间三角面片的点，使用公式24中同样的方法可以得到变形后的得到垂直方向的点后，就可以构建空间三角面片的边矢量矩阵v＝[v2-v1v3-v1v4-v1]和使用公式24得到形变梯度f3×3。通过对形变梯度f执行奇异值分解(singularvaluedecomposition，svd)得到f3×3＝u∑v^t，将奇异值矩阵∑带入公式26计算三角面片的firstpiola-kirchhoff应力张量p，其中p代表单位面积上的应力，应力的方向对应于v的列向量。

p＝2μ(∑-i)+λtr(∑-i)i(26)

当应力张量p中的最大应力超过了材料强度，需要在当前三角面片上生成新的裂口。首先定位当前三角面片的质心，以最大应力的方向(来自v的列向量)为裂口表面的法线，插入新的裂口。

当裂纹初始化之后，就可以在仿真过程中对裂纹进行延展操作。首先，通过对裂纹上的点使用公式23计算其应力强度因子ki，kii和kiii。然后，将ki，kii和kiii带入公式27得到有效应力强度keff(effectivestressintensity)。通过将有效应力强度keff与材料的断裂韧性kc进行对比，当keff大于kc时进行裂纹的延展。

在裂纹的延展过程中，需要计算延展的速度vcp和延展的角度θcp，可以通过公式28和公式30得到。在公式28中cr代表了rayleigh波速，ρ是材料的密度。为了计算延展角度θcp，需要先将ki和kiii通过公式29进行合并得到，这是由于ki和kiii主导了裂纹向前的延展，kii导致裂纹侧向旋转延展。将ki,iii和kii带入公式30得到了θcp，最后需要将延展角度θcp转换成全局坐标下的方向。

本方法原型系统的实现使用的软件平台为microsoftvisualstudio2010与opengl，硬件平台为有intelcorei73.60ghzcpu、nvidiageforcegtx770gpu、4g内存。方法效果图如图9，图10所示。

以上所述，仅是本发明的较佳实施例而已，并非是对本发明作其它形式的限制，任何熟悉本专业的技术人员可能利用上述揭示的技术内容加以变更或改型为等同变化的等效实施例应用于其它领域，但是凡是未脱离本发明技术方案内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与改型，仍属于本发明技术方案的保护范围。