基于深度神经网络与打靶算法的J2摄动Lambert问题求解方法与流程

基于深度神经网络与打靶算法的j2摄动lambert问题求解方法
技术领域
1.本发明属于轨道动力学技术领域，具体涉及一种基于深度神经网络与打靶算法的j2摄动lambert问题求解方法。


背景技术：

2.lambert问题是在给定始末端位置及飞行时间的情况下求解始末端的速度，是轨道动力学领域的基础问题。经典lambert问题是基于两体动力学模型提出的，但航天器的实际运动受到了各种摄动干扰，导致经典lambert问题的开普勒解无法满足实际任务的精度要求。因此，考虑j2摄动是中低轨道的主要摄动项，在经典lambert问题的基础上提出了j2摄动lambert问题。
3.根据求解原理，现有j2摄动lambert问题求解算法可以归纳为两类：解析法和打靶法。解析法的思路是推导j2摄动lambert问题的解析形式，将问题转化为一系列参数代数方程进行求解。打靶法则是根据末端状态误差反馈，利用各种打靶算法对初始速度矢量进行迭代修正。冯浩阳等人的大范围收敛的摄动lambert问题新型解法：拟线性化
‑
局部变分迭代法[j].航空学报,2021,42(x):324699中提出了一种拟线性化
‑
局部变分迭代法，通过拟线性化思想，将非线性两点边值问题转化为一系列具有一定迭代格式，并且成对出现的初值问题，进而通过局部变分迭代法对其进行求解，该方法的优点是利用拟线性化的大范围收敛特性和局部变分迭代法的快收敛、高精度特性，能够在在较大的时间和空间尺度下快速精确获得摄动lambert问题的初速度和转移轨道。但针对转移时间较长的多圈lambert问题，由于非线性特性增强，其线性化操作的误差将被放大，导致收敛性变差。yang z,luo y z,zhang j,et al.homotopic perturbed lambert algorithm for long
‑
duration rendezvous optimization[j].journal of guidance,control,and dynamics,2015,38(11):2215
‑
2223.中基于同伦技术提出了一种j2摄动多圈lambert问题求解方法，该方法的优点是引入了同伦技术有效地改善了算法的收敛稳定性，但同伦参数的引入也导致其迭代次数和计算时间大量增加。


技术实现要素：

[0004]
针对于上述现有技术的不足，本发明的目的在于提供一种基于深度神经网络与打靶算法的j2摄动lambert问题求解方法，以解决现有技术中在解决j2摄动lambert问题时计算效率低、收敛稳定性不足和多圈lambert问题求解效果差的问题。
[0005]
为达到上述目的，本发明采用的技术方案如下：
[0006]
本发明的一种基于深度神经网络与打靶算法的j2摄动lambert问题求解方法，步骤如下：
[0007]
1)根据始末端位置矢量和飞行时间，利用普适变量法求解二体lambert问题，得到始端速度初值，并基于得到的始端速度初值进行轨道递推，获取j2摄动干扰下的末端位置
误差；
[0008]
2)根据步骤1)得到的末端位置误差及初始条件中的始末端位置及飞行时间，利用训练得到的深度神经网络预估始端速度初值的误差，并以此为校正量修正步骤1)得到的始端速度初值，得到修正后的始端速度初始猜测值；
[0009]
3)以步骤2)得到的始端速度初始猜测值为初值，利用基于差分近似的牛顿迭代打靶算法对始端速度初始猜测值进行打靶修正，直至末端位置精度满足要求。
[0010]
进一步地，所述步骤1)具体包括：根据航天器的始末端位置矢量(r0,r
f
)和飞行时间tof，利用普适变量法求解二体lambert问题，得到始端速度初值v0；
[0011]
v0＝l(r0,r
f
,tof)
[0012]
式中，l表示lambert求解过程。
[0013]
进一步地，所述步骤1)具体还包括：根据得到的始端速度初值v0和已知的始端位置r0进行轨道递推，递推时间等于飞行时间，递推动力学模型采用j2摄动动力学模型，得到航天器实际到达的末端位置和速度矢量(r
a
,v
a
)，结合已知理想末端位置r
f
得到末端位置误差δr
f
＝r
f
‑
r
a
。
[0014]
进一步地，所述步骤2)中的深度神经网络的训练样本以始端位置矢量r0和基于二体lambert问题求解得到的始端速度初值v0、飞行时间tof及简单二体动力学下开普勒解的末端位置误差矢量δr
f
为输入，简单二体动力学下开普勒解的始端速度误差矢量δv0为输出，且所有位置和速度矢量均采用球坐标描述；始端速度初始猜测值为v
d
＝v0+δv0。
[0015]
进一步地，所述步骤2)中深度神经网络的训练样本获取步骤具体如下：
[0016]
21)随机生成初始轨道状态和飞行时间[r0；v
s0
；tof]；
[0017]
22)将初始状态[r0；v
s0
]在j2摄动动力学模型下递推，得到末端状态[r
f
；v
f
]；
[0018]
23)基于始末端状态和飞行时间参数，通过求解二体lambert问题，计算始端速度初值v0；
[0019]
24)以始端位置和始端速度初值为初始状态[r0；v0]，在j2摄动动力学模型下递推，得到实际末端位置r
a
；
[0020]
25)计算始端速度初值v0和末端位置r
a
的误差，δv0＝v
s0
‑
v0，δr
f
＝r
f
‑
r
a
；
[0021]
26)以始端位置矢量r0和始端速度初值v0、飞行时间tof及末端位置误差矢量δr
f
为输入，始端速度初值的误差矢量δv0为输出，形成训练样本，且所有矢量均在球坐标系下描述。
[0022]
进一步地，所述步骤2)中训练样本s的具体形式如下：
[0023]
s＝{[r
00
,α
r0
,β
r0
,v
00
,α
v0
,β
v0
,δr
ff
,δα
f
,δβ
f
,tof]，[δv
00
,δα0,δβ0]}
[0024]
其中，α和β分别表示矢量的方位角和极角，下标0和f分别为始末端标志，δv
00
＝||δv0||表示初始速度校正量的模长，r
00
＝||r0||表示始端位置的模长，δr
ff
＝||δr
f
||是末端位置误差的模长，则：
[0025][0026]
进一步地，所述步骤3)具体包括：使用差分近似方法计算雅克比矩阵，给始端速度矢量各分量分别施加一个小扰动δv＝10
‑6km/s；积分至末端状态并记录末端位置的偏差δr；得到的雅克比矩阵为：
[0027][0028]
则，始端速度修正量为：
[0029]
δv
i
＝j
‑1δr
fi
[0030]
式中，δr
fi
表示第i次迭代时的末端位置误差。
[0031]
本发明的一种基于深度神经网络与打靶算法的j2摄动lambert问题求解器，包括：
[0032]
一个或多个处理器；
[0033]
存储器，用于存储一个或多个程序；
[0034]
当所述一个或多个程序被所述一个或多个处理器执行时，使得所述一个或多个处理器实现上述求解方法。
[0035]
本发明的有益效果：
[0036]
本发明通过引入深度神经网络对二体lambert问题的开普勒解进行修正，极大地改善了初值的精度，进而有效减少了迭代打靶算法的迭代次数和计算时间，并确保了算法收敛的稳定性。而且，由于训练样本的转移时间不受约束，所以本发明在处理多圈j2摄动lambert问题时，依然能够在保证收敛稳定性的同时，维持高计算效率；整体思路新颖，具有广阔的应用前景。
附图说明
[0037]
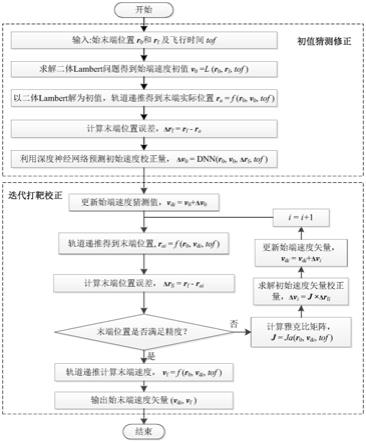
图1是本发明算法流程图。
[0038]
图2是本发明中打靶校正原理示意图。
[0039]
图3a是本发明中深度神经网络校正前后初始速度分量误差分布图。
[0040]
图3b是本发明中深度神经网络校正前后末端位置分量误差分布图。
[0041]
图4是应用本发明求解不同圈数j2摄动lambert问题的收敛情况示意图。
[0042]
图5是应用本发明求解不同圈数j2摄动lambert问题的时间消耗情况示意图。
具体实施方式
[0043]
为了便于本领域技术人员的理解，下面结合实施例与附图对本发明作进一步的说明，实施方式提及的内容并非对本发明的限定。
[0044]
参照图1所示，本发明的基于深度神经网络与打靶算法的j2摄动lambert问题求解
方法，步骤如下：
[0045]
1、已知航天器的始末端位置矢量(r0,r
f
)和飞行时间tof，利用普适变量法求解二体lambert问题，得到始端速度初值v0：
[0046]
v0＝l(r0,r
f
,tof)；
[0047]
2、根据步骤1计算得到的始端速度初值v0和已知的始端位置r0进行轨道递推，递推时间等于飞行时间，递推动力学模型采用j2摄动动力学模型，得到航天器实际到达的末端位置和速度矢量(r
a
,v
a
)，进而结合已知理想末端位置r
f
得到末端位置误差δr
f
＝r
f
‑
r
a
；
[0048]
3、根据已知的始端位置r0、飞行时间tof，始端速度初值v0和末端位置误差δr
f
，将涉及的矢量用球坐标描述并利用训练好的深度神经网络预测初始速度的校正量δv0：
[0049]
[δv
00
,δα0,δβ0]＝dnn(r
00
,α
r0
,β
r0
,v
00
,α
v0
,β
v0
,δr
ff
,δα
f
,δβ
f
,tof)
[0050]
其中，δv
00
＝||δv0||表示初始速度校正量的模长，r
00
＝||r0||表示始端位置的模长，v
00
＝||v0||是步骤1计算的初始速度的模长，δr
ff
＝||δr
f
||是末端位置误差的模长，α和β分别表示矢量的方位角和极角，下标0和f分别为始末端标志；
[0051]
利用下述公式将球坐标表示的矢量转化为笛卡尔直角坐标系描述：
[0052]
r0＝[r
00
sin(β
r0
)cos(α
r0
)；r
00
sin(β
r0
)sin(α
r0
)；r
00
cos(β
r0
)]
[0053]
v0＝[v
00
sin(β
v0
)cos(α
v0
)；v
00
sin(β
v0
)sin(α
v0
)；v
00
cos(β
v0
)]
[0054]
δr
f
＝[δr
ff
sin(δβ
f
)cos(δα
f
)；δr
ff
sin(δβ
f
)sin(δα
f
)；δr
ff
cos(δβ
f
)]
[0055]
δv0＝[δv
00
sin(δβ0)cos(δα0)；δv
00
sin(δβ0)sin(δα0)；δv
00
cos(δβ0)]
[0056]
神经网络预测效果主要由样本质量决定，本发明中样本的快速获取步骤具体如下：
[0057]
随机生成初始轨道状态和飞行时间[r0；v
s0
；tof]；
[0058]
将初始状态[r0；v
s0
]在j2摄动动力学模型下递推，得到末端状态[r
f
；v
f
]；
[0059]
基于始末端状态和飞行时间参数，通过求解二体lambert问题，得到始端速度初值v0；
[0060]
以始端位置和始端速度初值为初始状态[r0；v0]，在j2摄动动力学模型下递推，得到实际末端位置r
a
；
[0061]
计算始端速度初值v0和末端位置r
a
的误差，δv0＝v
s0
‑
v0，δr
f
＝r
f
‑
r
a
；
[0062]
以始端状态矢量r0和v0、飞行时间tof及末端位置误差矢量δr
f
为输入，始端速度初值的误差矢量δv0为输出，形成训练样本，且所有矢量均在球坐标系下描述。
[0063]
4、根据步骤3得到的初始速度修正量δv0，修正步骤1得到的始端速度初值v0，计算得到修正后的始端速度初始猜测矢量为v
d
＝v0+δv0；
[0064]
5、以步骤4计算得到的修正后的始端速度初始猜测值v
d
为初值，采用基于差分近似的牛顿迭代打靶算法对始端速度初始猜测值进行打靶修正，直至末端精度满足要求。如图2所示是步骤4牛顿迭代打靶过程示意图。
[0065]
本发明使用差分近似方法计算雅克比矩阵，具体过程如下：首先，给始端速度矢量各分量分别施加一个微小扰动δv＝10
‑6km/s；然后，积分至末端状态并记录末端位置的偏差δr；最终，得到的雅克比矩阵为：
[0066][0067]
则，始端速度修正量为：
[0068]
δv
i
＝j
‑1δr
fi
[0069]
其中，δr
fi
表示第i次迭代时的末端位置误差。
[0070]
则，第i次修正后的始端速度矢量v
di
＝v
di
‑1+δv
i
。
[0071]
本发明方法的实例：结合图3a、图3b、图4和图5说明本发明的实例验证，设定如下计算条件和技术参数：
[0072]
(1)以木星为中心天体，其中木星的平均赤道半径为r
j
＝71492km，木星引力常数为μ
j
＝126686543.922km3/s2，j2摄动项系数为j2＝0.01475。
[0073]
(2)随机样本的参数取值范围设定如下所示：
[0074][0075]
其中，r是初始轨道半径，e是初始轨道偏心率，i表示初始轨道倾角，ω表示初始升交点赤经，ω表示初始近地点幅角，u表示初始真近点角，tof表示飞行时间，t是初始轨道的轨道周期，(a是初始轨道半长轴)。
[0076]
(3)轨道末端位置打靶精度设定为0.001km。
[0077]
(4)深度神经网络包括四层隐含层，每层隐含层包含50个神经元，输入层包含10个神经元，输出层包含3个神经元，隐含层的激活函数采用双曲正弦函数(tanh)，输出层激活函数采用线性整流函数(relu)。
[0078]
(5)神经网络训练样本数量为200000，训练优化器选择自适应矩估计算法(adaptive moment estimation,adam)，最大训练次数为50000次，初始学习率设定为0.001。
[0079]
(6)monte carlo仿真次数设定为1000次。
[0080]
基于本发明的j2摄动lambert求解方法与上述设置的计算条件和技术参数，除神经网络训练采用python的tensorflow模块执行外，其他部分采用matlab软件进行仿真验证。图3a和图3b分别给出了深度神经网络校正前后初始速度矢量和末端位置矢量各分量的误差分布情况。经过神经网络的校正后，初始速度误差标准差不超过0.01km/s，末端位置分量误差不超过100km，初值精度得到了明显的改善。图4和图5分别对比了现有牛顿迭代打靶
算法、同伦迭代算法和本发明中采用的基于深度神经网络与打靶算法的j2摄动lambert问题求解算法在求解不同圈数j2摄动lambert问题时的收敛效果和计算时间。由图4可知，得益于神经网络提供的高精度初值，本发明随着圈数的增加依然能够稳定收敛。由图5可知，随着圈数增加本发明的计算时间略微增加，其增长趋势远小于同伦迭代算法，可见本发明在解决多圈j2摄动lambert问题时具备较高的计算效率。
[0081]
本发明具体应用途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进，这些改进也应视为本发明的保护范围。